煤礦井下群機器人高效任務分配算法

吳文臻

摘要：松散型合作群機器人系統在現階段煤礦輔助機器人作業中具有廣泛應用前景。但松散型合作群機器人系統的任務分配過程未向劃分過程進行反饋，導致任務劃分與分配過程高效性與合理性不足。針對該問題，提出一種基于改進型魯賓斯坦協商策略的煤礦井下群機器人高效任務分配算法。根據群機器人系統任務劃分與分配過程的多方博弈特點，將魯賓斯坦協商策略由雙方博弈向多方共同博弈方向延伸，提出多方協商博弈的“出價?討價?還價”規則。從機器人個體執行能力與任務執行情況差異的角度出發，提出基于機器人個體單位時間任務完成量的折扣因子計算方法，以及基于各分配周期任務執行情況的任務完成狀態反饋參數模型，以實現任務的動態劃分與分配。通過3組機器人合作執行煤礦礦區的整體監測任務，對算法性能開展實驗驗證，結果表明：①算法3（采用改進型魯賓斯坦協商策略）的任務劃分與分配效率較算法1（將每組無人機數量與運行速度乘積的比例直接作為3組無人機任務劃分與分配的標準）、算法2（使用多方共同協商的魯賓斯坦協商策略，但不考慮任務完成狀態反饋參數）分別提升了30.10%，18.29%。②基于算法3的3組無人機執行任務的平均最大時間差為42 s，較算法1、算法2分別優化了77.66%，65.29%，這是由于算法3通過引入任務完成狀態反饋參數，及時對任務參與方的任務執行過程進行評估，將任務的分配和執行過程向任務的劃分階段進行反饋，使任務的劃分與分配更加準確。

關鍵詞：煤礦井下群機器人；松散型合作群機器人；魯賓斯坦協商策略；任務劃分與分配；折扣因子；狀態反饋

中圖分類號： TD67??? 文獻標志碼： A

Efficient task assignment algorithm for coal mine underground group robots

WU Wenzhen1，2

（1. CCTEG China Coal Research Institute ， Beijing 100013， China；2. State Key Laboratory ofHigh Efficient Mining and Clean Utilization of Coal Resources， Beijing 100013， China）

Abstract： The loose cooperative group robot system has broad application prospects in the current coal mine auxiliary robot operation. However， the task assignment process of the loose cooperative group robot system did not provide feedback to the division process， resulting in insufficient efficiency and rationality of the task division and assignment process. To address this issue， an efficient task assignment algorithm for coal mine underground group robots based on an improved Rubinstein negotiation strategy is proposed. Based on the multi-party game features of task division and assignment in group robot systems， the Rubinstein negotiation strategy is extended from a bipartite game to a multi-party joint game. A "bid-bargain-counteroffer" rule for multi-party negotiation games is proposed. From the perspective of the difference between the execution capability and task execution status of individual robots， a discount factor calculation method based on the task completion quantity per unittime of robot individuals is proposed. A task completion status feedback parameter model based on the task execution status of each assignment cycle is also proposed to achieve dynamic task division and assignment. By collaborating with three groups of robots to perform overall monitoring tasks in coal mining areas， experimental verification is conducted on the performance of the algorithm. The results show the following points.① Algorithm 3 uses an improved Rubinstein negotiation strategy. Algorithm 1 directly uses the ratio of the number of unmanned aerial vehicles in each group multiplied by their running speed as the standard for task division and assignment in three groups of unmanned aerial vehicles. Algorithm 2 uses the Rubinstein negotiation strategy of multi-party negotiation without considering the feedback parameters of task completion status. Algorithm 3 has a higher efficiency in task division and assignment than Algorithm 1 and Algorithm 2 by 30.10% and 18.29% respectively.② The average maximum time difference for the three groups of unmanned aerial vehicles based on Algorithm 3 to execute tasks is 42 seconds. It is 77.66% and 65.29% optimized compared to Algorithm 1 and Algorithm 2， respectively. This is because Algorithm 3 introduces task completion status feedback parameters to timely evaluate the task execution process of the task participants. Algorithm 3 provides feedback on the task assignment and execution process to the task division stages， making the task division and assignment more accurate.

Key words： coal mine underground group robots; loose cooperative group robots; Rubinstein negotiation strategy; task division and assignment; discount factor; state feedback

0 引言

機器人在煤炭行業的應用研究是煤礦智能化技術創新的關鍵方向。作為機器人的核心組成部分，移動機器人已逐漸滲透到“采、掘、機、運、通”等煤礦生產的各個環節[1]。尤其是在面對如礦井采空區沉降監測、井下大面積危險區域監測等可并行完成的任務時，由多個具備簡單結構與功能的同構機器人單元組成的群機器人系統可在任務執行效率方面展現出巨大優勢[2]。在群機器人系統中，機器人單元之間的合作方式分為緊密型和松散型2種。緊密型合作方式主要基于行為技術、虛擬向量場技術實現機器人單元的高度協調運作，需要實時預知與優化多種因素，因此主要應用于機器人編隊保持或合作搬運等強實時協作場景；松散型合作方式主要基于不同類型任務分配策略，在每個任務執行周期初始階段實現機器人單元的任務分配，由于其對機器人單元實時性配合要求低，更適用于礦山救援、環境探測、災害監測等任務中的未知區域探索和地圖構建等場景[3-5]。因此，松散型合作群機器人系統在現階段煤礦輔助機器人作業中有廣泛應用前景。

松散型合作群機器人系統中，任務被劃分為多個子任務，并分配至群機器人系統中的機器人單元分別執行。任務劃分是以機器人單元的預定義任務執行成本為基礎。在任務分配完成后，機器人單元自身任務執行能力是任務執行效果最大的影響因素[6]。由于松散型合作方式關注的重點是任務分配問題，其任務劃分過程被假定為已經在協作技術框架外完成，所以松散型合作的主要缺點是任務分配過程與任務劃分過程不是一體化，任務分配過程不會向任務劃分過程進行反饋，導致任務分配過程中遇到的錯誤不能被及時修正[7-8]，進而導致任務的整體執行周期過長，即任務執行高效性不足，同時任務執行過程中機器人個體的空閑率過高，即任務分配合理性不足。例如松散型合作方式中運用最廣泛的任務分配算法——合同網算法中，每個機器人單元會根據預定義的成本和收入函數來計算每個任務的預期收益和損失，然而機器人單元的偏好和限制等因素只在任務分配階段被考慮，并沒有在任務劃分階段考慮，導致任務分配的合理性不足[9]。

魯賓斯坦協商策略是博弈論方面的合作博弈模型，沒有第三方強制結束機制與任何附加基礎，最終分配結果完全由博弈參與方自身因素決定，可兼顧所有博弈參與方最大利益[10]。魯賓斯坦協商策略主要用于解決雙方合作之前對總任務量的分配問題，用完全信息動態博弈方法模擬基本的、無限期的完全信息討價還價過程，并據此將整個博弈建立為完全信息輪流“出價?討價?還價”模型[11]。

針對群機器人系統在任務劃分與分配過程中高效性與合理性不足的問題，本文將魯賓斯坦協商策略與群機器人系統松散型合作方式的任務劃分與分配相融合，提出煤礦井下群機器人高效任務分配算法。首先，將魯賓斯坦協商策略由雙方博弈向多方共同博弈方向延伸；然后，基于機器人個體的不同執行能力及當前任務的執行情況，融入表示任務完成狀態的反饋參數，構建折扣因子計算模型，最終實現任務的動態劃分與分配；最后，通過3組機器人共同合作執行煤礦礦區整體監測任務，對算法的任務劃分與分配策略進行驗證，并對算法的高效性與合理性展開實驗驗證。

1 魯賓斯坦協商策略基本理論

在魯賓斯坦協商策略中，根據輪流“出價?討價?還價”模型，參與協商博弈的雙方輪流提出希望得到的份額。博弈從發起者開始，得到報價的一方可選擇接受報價，即最終達成協議，也可選擇拒絕報價，并向對方提出新的報價。博弈過程會一直持續下去，直到博弈雙方最終達成協議。該博弈過程參與方的出價方式都是加密的，每個參與方都不會掌握對方準確的出價方式，且通過運用魯賓斯坦協商策略能夠保證參與博弈的雙方最終達成協議[12-13]。

1.1 折扣因子

在魯賓斯坦協商策略模型中，參與雙方都有一個與其自身特征相匹配的折扣因子，折扣因子越小，通過博弈最終所得任務份額越少。折扣因子為參與方的加密信息，對方無法得到該信息。假設總任務量為1，參與雙方首次提出的任務份額均接近總任務量（一般取總任務量的99%），且提出的任務份額隨博弈輪數的增加逐漸減小。隨著博弈的進行，提出報價的參與方新要求的任務份額 K 與上一輪要求任務份額 L 之間關系為[14-15]

K =δL??????? （1）

式中δ為折扣因子，0<δ＜1。

將協商發起者和響應者的折扣因子分別記為δ1和δ2，首次提出的任務份額分別記為p和q，協商過程如圖1所示。發起者先出價p，響應者可以接受或拒絕1-p的份額。如果響應者接受，則博弈結束，博弈結果按發起者提出的方案執行；如果響應者拒絕，則響應者出價（還價）q，發起者可以接受或拒絕 1- q 的份額；如果發起者接受，則博弈結束，博弈結果按響應者提出的方案執行；如果發起者拒絕，發起者再出價δ1p；如此持續進行下去，直到參與博弈的某一方出價被另一方接受為止。因此這是一個無限期完全信息博弈，發起者在輪數1，3，5，…出價，響應者在輪數2，4，6，…出價。

1.2 博弈平衡

魯賓斯坦協商策略的博弈過程長度不確定，通過運用有限階段逆向歸納法可獲取博弈平衡點[16]。假設在第i（i≥3）輪博弈時參與人1出價M，參與人2在得到份額為1- M后達成協議。當第i輪博弈時的 M 等價于第i-1輪博弈時的δ1 M，參與人2在第 i-1輪博弈時得到1-δ1 M。同理，當第i-1輪博弈時的1-δ1 M等價于第i-2輪博弈時的δ2（1-δ1 M），參與人1在第i-2輪博弈時得到1-δ2（1-δ1 M），如圖2所示，因此可得博弈結束時參與人1理論上能夠得到的份額，即理論博弈平衡點 M。

由于參與雙方出價策略具有保密性，博弈過程中雙方無法通過理論博弈平衡點判斷博弈是否結束，所以只能通過參與博弈的某一方判斷對方的剩余報價是否大于自身在下一輪博弈中準備提出的報價，如果大于自身準備提出的報價，則博弈結束，否則進行下一輪的博弈[17-18]。

2 基于改進型魯賓斯坦協商策略的群機器人任務劃分與分配算法

群機器人任務劃分與分配問題可看作多方合作博弈的過程。根據群機器人系統的工作特點，遵循魯賓斯坦協商策略中提出的輪流“出價?討價?還價”思想，將魯賓斯坦協商策略參與方的數量由限定的雙方協商向多方共同協商的方向進行拓展延伸，通過對任務完成的狀態進行實時反饋，使群機器人在任務劃分與分配過程中體現出高效性和合理性[19]。

2.1 多方共同協商博弈過程

基于改進型魯賓斯坦協商策略的群機器人任務采用“循環出價，末位決定”原則進行博弈。在n個參與方共同博弈的過程中，由前n-1個參與方分別提出希望得到的份額，第n個參與方選擇接受或拒絕，如果選擇接受，則博弈結束，博弈結果按照前n-1個參與方提出的份額進行劃分與分配；如果選擇拒絕，則第n個參與方與前n-2個參與方再分別提出希望得到的份額，第n-1個參與方選擇接受或拒絕，如果選擇接受，則博弈結束，博弈結果按前n-2個參與方與第 n個參與方提出的份額進行劃分與分配；如果選擇拒絕，則前n-3個與后2個參與方再分別提出希望得到的份額，第n-2個參與方選擇接受或拒絕；依此類推，直到最終任務劃分與分配份額被所有參與方接受為止[20]。

以3方共同協商博弈為例（圖3），將協商參與方的折扣因子分別記為δ1，δ2，δ3，首次提出的任務份額分別記為 X，Y，Z。第1輪博弈由參與方 A 和參與方 B 先出價，參與方 C 可以接受或拒絕。如果參與方 C 接受，則博弈結束，博弈結果按照參與方 A 和參與方 B 提出的方案執行；如果參與方 C 拒絕，第2輪博弈開始，參與方 C 和參與方 A 共同出價（還價），參與方 B 可以接受或拒絕；如果參與方 B 接受，則博弈結束，博弈結果按參與方 C 和參與方 A 提出的方案執行；如果參與方 B 拒絕，第3輪博弈開始，參與方 B 和參與方 C再出價；如此一直進行下去，直到出價被3個參與方都接受為止。

2.2 折扣因子計算模型

折扣因子δ表示任務參與方對任務的執行能力，是根據各參與方的自身特征來確定的加密參數，對任務最終的分配比例起著決定性作用。折扣因子的影響因素有諸多方面，每個影響因素的變化對折扣因子造成的影響程度差別很大。根據任務的不同，將影響因素分為主要部分和次要部分，這里只考慮對任務劃分有較大影響的主要部分。

如果影響因素大小與單位時間內完成的任務量成正比，則隨著影響因素數值增大，單位時間內完成的任務量變化趨勢為遞增（如果影響因素大小與單位時間內完成任務量成反比，則取影響因素的倒數作為其數值）。任取多個對數型、指數型及比例型3種典型遞增模式的影響因素進行分析，如圖4所示。首先給出影響因素數值x與單位時間完成的任務量f 之間的關系，可知隨著不同影響因素數值的增大，單位時間內完成任務量的遞增趨勢差別較大。完成單位任務量所需時間為t，則t和f 之間的關系為 t =1/ f ，則基于x與f 之間的變化關系，可得影響因素數值x與t 的關系，當x一定時，t越大表示任務完成效率越低。

基于x與t 的變化關系，用折扣因子δ表示1- t，即表示影響因素對任務的影響能力，可得影響因素數值x與其折扣因子δ的關系，如圖5所示。可看出隨著影響因素數值增大，如果單位時間內完成任務量增大的幅度越大，即折扣因子增長越快，則該影響因素對任務的影響能力就越大，意味著該影響因素越影響因素數值x與折扣因子δ間的關系為

式中r為影響因素的權重系數，0＜r≤1，r 越大，單位時間完成的任務量越多，折扣因子越大，即越重要。

以指數型、對數型及比例型3種典型增長曲線為例，對影響因素數值x與折扣因子δ之間的關系進行驗證，結果如圖6所示。首先取3種影響因素數值x與單位時間完成任務量f 的數據，分別滿足上述3種典型類型變化趨勢，如圖6（a）所示。根據影響因素數值x、完成單位任務量所需時間t及折扣因子δ之間的轉換關系，可得影響因素數值x與其折扣因子δ關系，如圖6（b）所示。可看出隨著影響因素數值增大，指數型增長模式在單位時間內完成任務量增大幅度最大，折扣因子增長最快，即該影響因素重要性最大，比例型增長次之，對數型增長最小。

分別為3種影響因素選取合適權重系數，代入式（3）進行驗證，其中指數型增長的權重系數 r1=0：078，對數型增長 r2=0：009，比例型增長 r3=0：025，將所得的計算結果與圖6（b）中理論結果進行對比，結果如圖7所示。可看出折扣因子計算結果與理論結果之間的誤差在0.02范圍內，所以在權重系數選擇恰當的前提下，式（3）可對影響因素與折扣因子間的關系進行較好描述。

由于影響因素之間是耦合的，針對多個影響因素對折扣因子產生的影響，影響因素數值x與折扣因子δ的關系為

式中：k為任務完成狀態反饋參數；m為影響因素總數；xj為第j 個影響因素數值；rj為第j 個影響因素的權重系數。

在折扣因子中引入任務完成狀態反饋參數k，對上一個分配周期任務執行情況進行評估，根據評估結果對任務劃分與分配情況進行調整，使群機器人系統最大限度地發揮自身任務執行能力，進而高效完成任務。任務完成狀態反饋參數k為

式中：W為任務執行度參數，表示在上一個分配周期中完成的任務量與分配總任務量比值；Waverage為平均任務執行度參數，表示上一個分配周期中所有任務參與方任務執行度參數的算術平均數。

第1個分配周期（任務劃分的初始階段）進行任務劃分與分配時k =1。

2.3 多方協商平衡

改進型魯賓斯坦協商策略的最大特點是任務劃分與分配由原來的雙方進行博弈改進為多方博弈。由于最終的博弈平衡需要滿足所有參與方的需求份額，所以其博弈過程更為復雜，持續時間更長。

改進型魯賓斯坦協商策略基于有限階段逆向歸納法尋找多方博弈的理論協商博弈平衡點：n個參與方進行博弈，每個參與方的折扣因子分別為δ1?δn，博弈過程如圖8所示。在第i（i≥n）輪博弈時編號為1?n-1的參與方分別出價M1?Mn-1，編號為n的參與方得到剩余份額s0后達成協議。因為第i輪博弈時的 M1等價于第i-1輪博弈時的δ1 M1，參與方n在第i-1輪博弈時最多得到sn；因為第i-1輪博弈時的M2等價于第i-2輪博弈時的δ2 M2，參與方1在第i-2輪博弈時至少得到 s1；因為第 i-2輪博弈時的 M3等價于第 i-3輪博弈時的δ3 M3，參與方2在第i-3輪博弈時至少得到 s2；依次類推，在第i-n+1輪博弈時的sn等價于第i-n輪博弈時的δnsn，參與方n-1在第i-n輪博弈至少得到sn-1。

根據第i輪博弈時各參與方所得份額等價于第i一 n輪博弈時所得的份額，可得

該方程組的未知數分別為參與人1?n 的所得份額M1?Mn，求解該方程組即可得出參與人1?n 通過改進型魯賓斯坦協商策略進行博弈后所得的理論協商博弈平衡點。

3 實驗驗證

以工業級四旋翼無人機組共同完成某煤礦礦區整體監測任務作為實驗背景，對基于改進型魯賓斯坦協商策略的群機器人任務劃分與分配算法的高效性與合理性進行驗證。工業級四旋翼無人機外形與視角如圖9所示，技術參數見表1。在任務執行過程中，當完成任務劃分與分配后，運用Web+GIS技術自動生成和優化作業航線。運用電子圍欄與飛行控制系統相配合的方式規劃作業區域和禁飛區域，其中任務區域的總面積為3.498 m2。無人機群依據規劃航線自主飛行，實現任務區域遍歷[21-22]。

實驗準備階段，將13架無人機分為3組，每一組作為一個參與方參與任務劃分與分配過程的博弈。對每組無人機的最大運動速度進行限制，使無人機的飛行能力實現差異化。3組無人機的個數與飛行速度見表2。

3.1 第1個分配周期的任務比例分配

進行任務區域劃分前需確定3組無人機的初始折扣因子。主要影響因素有每組無人機數量和運行速度，取無人機數量權重系數r1=0：95，機器人運行速度權重系數 r2=0：85，任務完成狀態反饋參數 k =1。根據式（4）可得3組無人機的初始折扣因子分別為δ1=0：9823，δ2=0：9765，δ3=0：9655。設每一次任務劃分與分配周期為120 s，總任務份額為1，在明確任務區域的總面積和3組無人機的折扣因子后，根據式（6）可得3組無人機的理論協商博弈平衡點，分別為0.3635，0.3256，0.3109。

根據3組無人機的參數，運用改進型魯賓斯坦協商策略對任務份額進行劃分，博弈過程如圖10所示。博弈共進行了47輪，在第1輪博弈中，第1組和第2組無人機的初始出價（期望份額）為0.49，則第3組無人機得到的初始份額為0.02，小于其在第2輪博弈中準備提出的報價0.49，則3組無人機進入第2輪的博弈。依此類推，第2組無人機得到的報價為0.3360，大于其在下一輪博弈中準備提出的報價0.3351，則博弈過程結束，3組無人機得到博弈的平衡。在第1個分配周期的初始階段，3組無人機分配的任務份額分別為0.3748，0.3360，0.2892，與理論協商博弈平衡點相比，誤差份額保持在0.05范圍內。誤差產生的原因是，通過式（6）只需要經過1步計算即可得出理論博弈平衡點，但實際平衡點需要通過多步協商博弈獲取，每一步計算產生的誤差均會得到累計。

由于任務執行過程中受風速、任務區域輪廓等因素影響，第1個分配周期中每組無人機對分配所得任務的完成情況有較大差別。第1個分配周期結束后任務區域的剩余面積，即第2個分配周期任務區域總面積為3.303 km2。

根據式（5）計算第1個分配周期的任務完成狀態反饋參數，對3組無人機的任務執行情況進行評估，根據評估情況對折扣因子進行適應性調整。第1個分配周期中3組無人機對任務的完成情況與狀態反饋參數見表3。將k代入式（4），可得3組無人機的折扣因子：δ1=0：9859，δ2=0：9762，δ3=0：9538。

3.2 剩余分配周期的任務比例分配

在第2個分配周期的初始階段，根據第2個分配周期的任務區域面積和3組無人機的折扣因子，運用改進型魯賓斯坦協商策略對任務區域進行新一輪的劃分與分配，在進行了44輪博弈后得到協商博弈平衡，3組無人機獲得的任務份額分別為0.4022，0.3449，0.2529。

3組無人機共同執行礦區整體監測任務共經歷15個分配周期。每組無人機在不同分配周期的任務完成情況如圖11所示。受外界（如地形、氣候等不可抗拒因素）影響，同一組無人機在不同分配周期完成的任務量相差較大，除第15個分配周期外，第1組無人機在單個分配周期完成任務量 task_1變化范圍為0.0714～0.1258 km2，第2組無人機在單個分配周期完成任務量 task_2的變化范圍為0.0524～0.1008 km2，第3組無人機在單個分配周期完成任務量 task_3的變化范圍為0.0412～0.0829 km2。

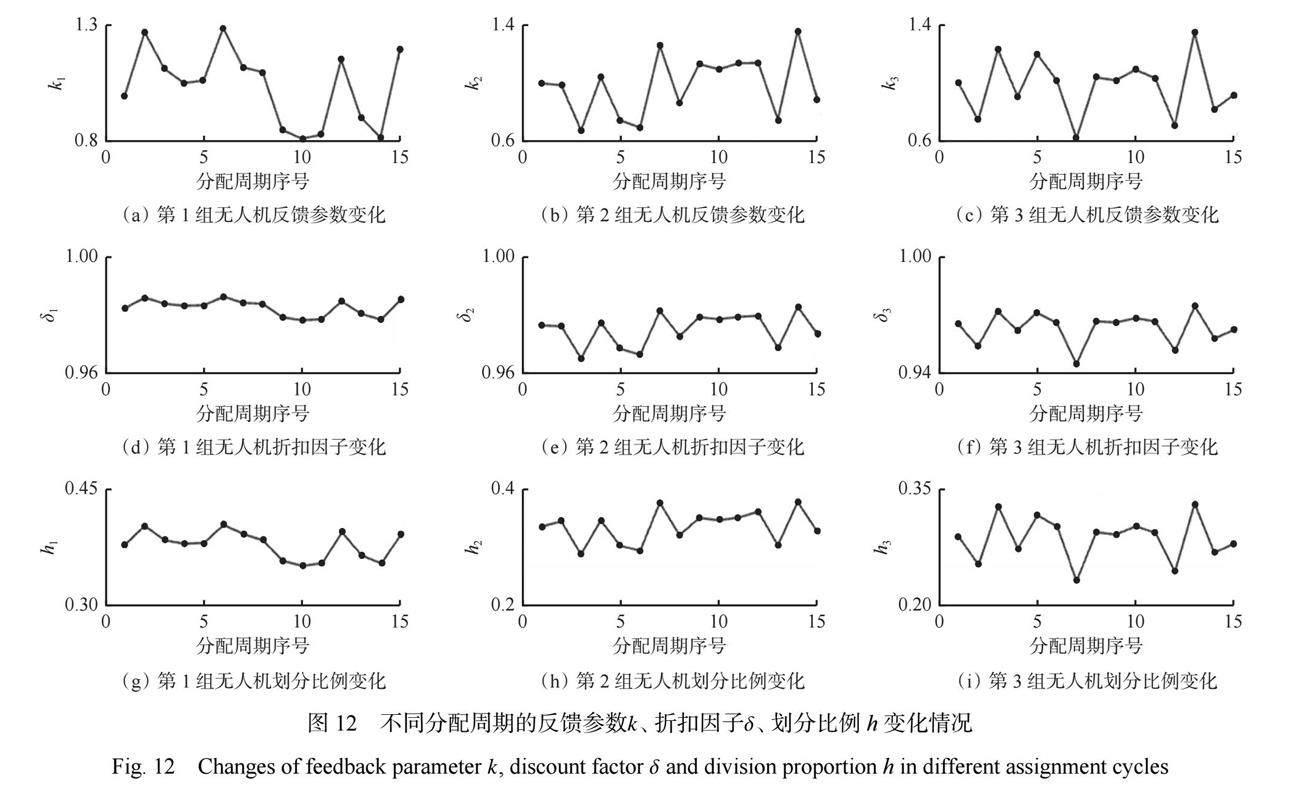
在每個分配周期初始階段，通過分析上個分配周期中每組無人機任務執行情況，即每組無人機的執行水平與任務總體執行水平之間的關系，確定任務完成狀態反饋參數k。通過式（4）對折扣因子δ進行調整，進而通過改進型魯賓斯坦協商策略對每個任務分配周期的任務劃分比例p進行調整。任務執行過程中，在任務比例劃分階段，3組無人機在不同分配周期的反饋參數k、折扣因子δ、劃分比例 h 的變化情況如圖12所示。可看出劃分比例 h 的變化趨勢與任務完成狀態反饋參數k的變化趨勢基本相符，即在前一個分配周期中任務執行水平較高的無人機組，在下一周期中所分配的任務量會隨之增大，相反地，任務執行水平較低的無人機組在下一周期中分配的任務量隨之降低，實現了執行能力的最大化。

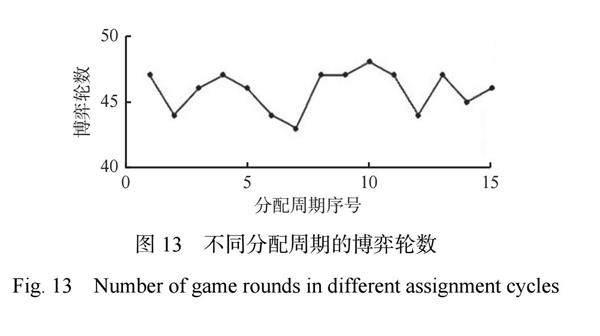
不同分配周期的博弈輪數如圖13所示，可看出運用改進型魯賓斯坦協商策略，每個分配周期的博弈輪數保持在40～50之間，穩定地解決了區域遍歷任務過程中的任務劃分分配問題。

3.3 不同任務劃分與分配算法高效性與合理性對比實驗

為了比較算法在任務劃分與分配方面的高效性，分別運用3種不同的任務劃分與分配算法進行煤礦礦區整體監測任務實驗，實驗中設置相同的無人機數量、運行速度及任務區域面積。每種任務劃分與分配算法分別進行3次實驗，取3次實驗經歷的平均時間作為參考。

算法1通過計算每組無人機數量與運行速度的乘積，將乘積的比例直接作為3組無人機任務劃分與分配的標準，即每組無人機分配的任務份額分別為0.4412，0.3330，0.2258；算法2使用多方共同協商的魯賓斯坦協商策略，但不考慮任務完成狀態反饋參數k，任務的分配和執行過程不會向任務劃分過程進行反饋，3組無人機分配的任務份額始終為0.3748，0.3360，0.2892；算法3采用改進型魯賓斯坦協商策略，實現任務的動態劃分與分配。由于無人機續航能力弱的缺點不可避免，無人機電池更換時間不在實驗計時范圍內。

通過對總體任務執行過程進行計時，實現對3種不同任務劃分與分配算法高效性的對比。基于3種算法的任務執行過程所經歷的時間見表4。可看出算法3的任務劃分與分配效率較算法1、算法2分別提升了30.10%，18.29%。

通過對每組無人機的任務執行過程進行計時，實現對3種不同的任務劃分與分配算法合理性的對比。每組無人機的平均任務執行時間見表5。可看出基于算法1的3組無人機執行任務的平均最大時間差為188 s，即無人機組在執行完任務之后平均有188 s 的等待時間，這段時間內部分無人機組處于空閑狀態，而部分無人機一直處于任務執行狀態；同理，基于算法2的3組無人機執行任務的平均最大時間差為121 s，這是由于算法2運用了多方共同協商的魯賓斯坦協商策略，該策略通過折扣因子優化了影響因素（無人機數量和運行速度）與任務劃分與分配結果之間的關系，避免了影響因素隨著其數值增大導致的冗余問題；基于算法3的3組無人機執行任務的平均最大時間差為42 s，較算法1、算法2分別優化了77.66%，65.29%，這是由于算法3通過引入任務完成狀態反饋參數k，及時對任務參與方的任務執行過程進行評估，將任務的分配和執行過程向任務的劃分階段進行反饋，使任務的劃分與分配更加準確。

由實驗結果可知，運用改進型魯賓斯坦協商策略對任務進行劃分與分配，能夠最大化地發揮群機器人的任務執行能力，體現了改進型魯賓斯坦協商策略在任務劃分與分配方面的高效性和合理性優勢。

4 結論

1）將魯賓斯坦協商策略中的雙方博弈向多方共同博弈的方向拓展延伸；以對任務最終分配起決定性作用的影響因素為研究對象，提出了折扣因子計算方法，根據該方法能夠量化參與方對任務的執行能力；在折扣因子中引入任務完成狀態反饋參數，通過評估對所分配任務的執行程度，對任務劃分與分配情況進行調整。

2）基于3組無人機合作開展煤礦礦區監測任務實驗，對算法的高效性與合理性進行了驗證。驗證結果表明：算法3的任務劃分與分配效率較算法1、算法2分別提升了30.10%，18.29%；基于算法3的 3組無人機執行任務的平均最大時間差為42 s，較算法1、算法2分別優化了77.66%與65.29%。

參考文獻（References）：

[1] 張鵬.智能礦山機器人協同管控[J].工礦自動化，2021，47（增刊2）：43-44.

ZHANG Peng. Collaborative control of robots in intelligent mine[J]. Industry and Mine Automation，2021，47（S2）：43-44.

[2] 王宏，宋智瀛，賈瑞清.基于模塊化異構多機器人的煤礦災害處置系統[J].煤炭科學技術，2011，39（10）：93-95，111.

WANG Hong， SONG Zhiying，JIA Ruiqing. Mine disaster control system based on module heteromerous multi robot[J]. Coal Science and Technology，2011，39（10）：93-95，111.

[3] GAUTHAM D，THOMAS M，SONYA C，et al. A distributed task allocation algorithm for a multi-robot system in healthcare facilities[J]. Journal of Intelligent & Robotic Systems，2015，80（1）：33-58.

[4] 彭凡彬，楊俊杰，葉波.改進蟻群算法的變電站群機器人路徑規劃研究[J].儀表技術，2018（3）：9-13，35.

PENG Fanbin，YANG Junjie，YE Bo. Research on robot path planning of substation group based on improved ant colony algorithm[J]. Instrumentation Technology，2018（3）：9-13，35.

[5] 王偉嘉，鄭雅婷，林國政，等.集群機器人研究綜述[J].機器人，2020，42（2）：232-256.

WANG Weijia，ZHENG Yating，LIN Guozheng，et al. Swarm robotics：a review[J]. Robot，2020，42（2）：232-256.

[6] XIAO Renbin，WU Husheng，HU Liang，et al. A swarm intelligence labour division approach to solving complex area? coverage? problems? of swarm? robots[J]. International Journal of Bio-Inspired Computation，2020，15（4）：224-238.

[7] 邱靖廷.基于群體智能的多機器人任務分配[D].哈爾濱：哈爾濱工程大學，2020.

QIU Jingting. Multi-robot task assignment based on group intelligence[D]. Harbin： Harbin Engineering University，2020.

[8] YEUNG W L. Efficiency of task allocation based on contract net protocol with audience restriction in a manufacturing control application[J]. International Journal of Computer Integrated Manufacturing，2018，31（10）：1005-1017.

[9] 梁志偉，吳海健. RoboCup標準平臺組中基于改進合同網協議的任務分配算法[J].計算機工程與科學，2022，44（1）：176-183.

LIANG Zhiwei， WU Haijian. A task allocation algorithm based on the improved contract network protocol in RoboCup standard platform league[J]. Computer Engineering & Science，2022，44（1）：176-183.

[10] 黃柳強，秦麗娟，商云龍.電力市場雙邊協商交易模型設計研究[J].廣西電力，2021，44（2）：14-19.

HUANG Liuqiang， QIN Lijuan， SHANG Yunlong. Research on a design of bilateral negotiation and transaction model in electricity market[J]. Guangxi Electric Power，2021，44（2）：14-19.

[11] 馬金龍. 基于博弈論的國際工程承包合同糾紛研究[D].北京：北京交通大學，2020.

MA Jinlong. Research on the disputes of international engineering contracts based on game theory[D]. Beijing：Beijing Jiaotong University，2020.

[12] 羅震環.基于VCG和魯賓斯坦模型的數據定價方法研究[D].哈爾濱：哈爾濱工業大學，2021.

LUO Zhenhuan. Research on data pricing methods based on VCG and rubinstein models[D]. Harbin：Harbin Institute of Technology，2021.

[13] JAEHWI S， HOUNG S. Bargaining model-based coverage area subdivision of multiple UAVs in remote sensing[J]. Journal of Biosystems Engineering，2021，45（3）：133-144.

[14] 張夢穎，王蒙一，王曉東，等.基于改進合同網的無人機群協同實時任務分配問題研究[J].航空兵器，2019，26（4）：38-46.

ZHANG? Mengying， WANG? Mengyi，WANGXiaodong，et al. Cooperative real-time task assignment of UAV group based on improved contract net [J]. Aero Weaponry，2019，26（4）：38-46.

[15] 馬洪寬.博弈論[M].上海：同濟大學出版社，2015：78-91.

MA Hongkuan. Game theory[M]. Shanghai：Tongji University Press，2015：78-91.

[16] 王磊.動態合作博弈中解的策略穩定性[D].青島：青島大學，2016.

WANG Lei. Strategic stability of solutions in dynamic cooperative games[D]. Qingdao：Qingdao University，2016.

[17] 郭超，熊偉，劉呈祥.合同網協議改進研究現狀與展望[J].裝備學院學報，2016，27（6）：82-89.

GUO Chao，XIONG Wei，LIU Chengxiang. Prospects and current researches on improvement of contract net protocol[J]. Journal of Equipment Academy，2016，27（6）：82-89.

[18] SZCZERBA R J，GALKOWSKI P，GLICKSTEIN I S， et al. Robust algorithm for real-time route planning[J].IEEE Transactions on Aerospace and Electronic Systems，2000，36（3）：869-878.

[19] 劉剛，王瑛，張發，等.合同網協議協商機制收斂性與收斂速率分析[J].控制與決策，2014，29（6）：1027-1034.

LIU Gang， WANG Ying， ZHANG Fa， et al. Convergence and convergent rate analysis of contract net protocol negotiation mechanism[J]. Control and Decision，2014，29（6）：1027-1034.

[20] 李娟，張昆玉.基于改進合同網算法的異構多AUV協同任務分配[J].水下無人系統學報，2017，25（6）：418-423.

LI Juan，ZHANG Kunyu. Heterogeneous multi-AUV cooperative task allocation based on improved contract net algorithm[J]. Journal of Unmanned Undersea Systems，2017，25（6）：418-423.

[21] 吳江，趙世鈺，周銳，等.基于面向服務的多無人機輔助決策仿真集成方法[J].系統仿真學報，2012，24（12）：2525-2529.

WU Jiang，ZHAO Shiyu，ZHOU Rui，et al. Simulation integration of decision aiding based on service-oriented for multiple UAVs[J]. Journal of System Simulation，2012，24（12）：2525-2529.

[22] CHEN Kaiwen，REICHARD G，AKANMU A，et al. Geo-registering UAV-captured close-range images to GIS-based? spatial? model? for? building? facade inspections[J]. Automation in Construction，2021，122（1）. DOI：10.1016/j.autcon.2020.103503.