想吃上烙餅,先掌握概率
2023-04-29 00:44:03大力
童話王國·奇妙邏輯推理 2023年3期
關鍵詞:游戲
大力
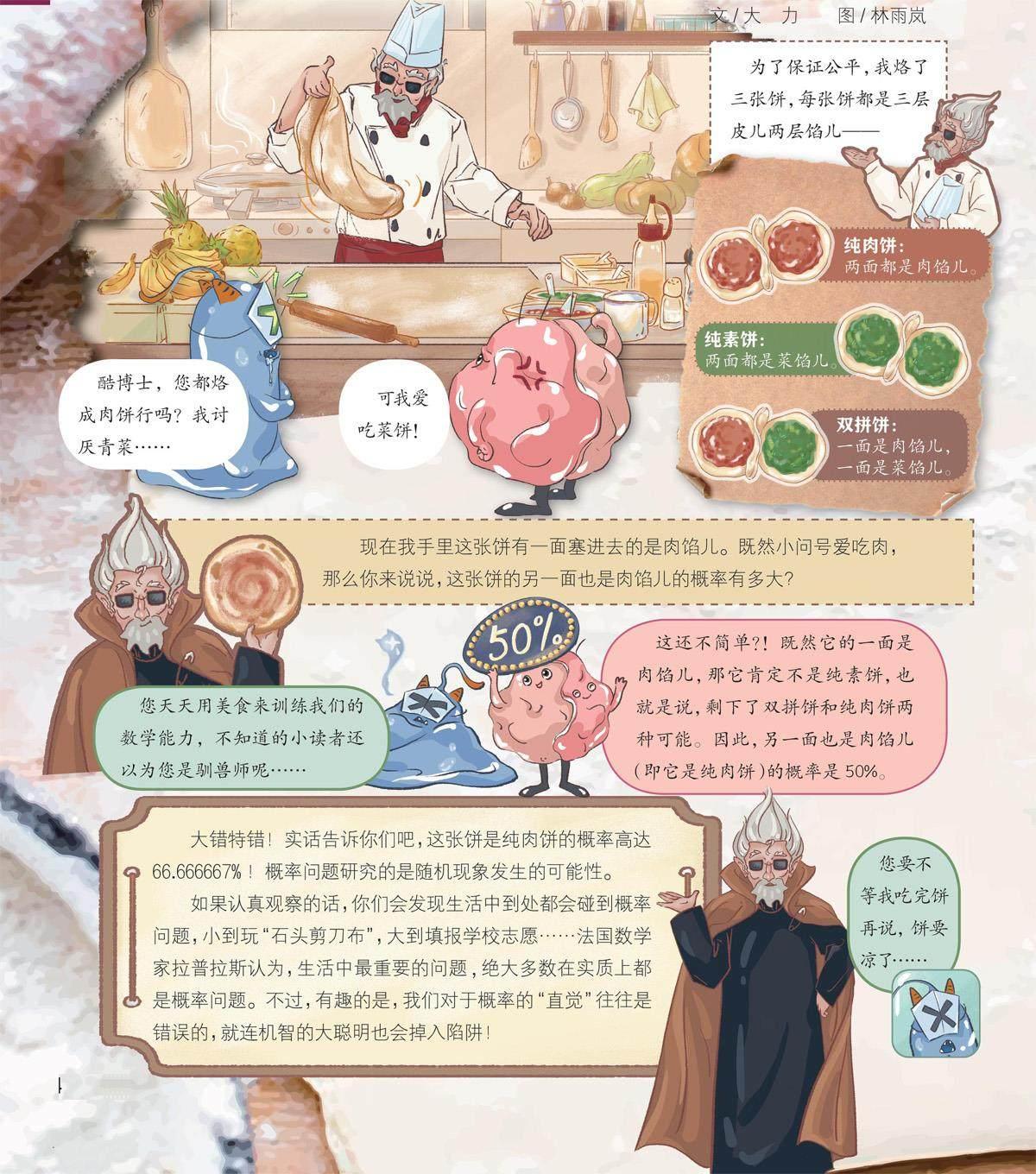
現在我手里這張餅有一面塞進去的是肉餡兒。既然小問號愛吃肉,那么你來說說,這張餅的另一面也是肉餡兒的概率有多大?
我的推導過程聽上去沒什么問題,但是我的算法忽略了一個事實——當我們得知這張餅的一面是肉餡兒時,我們并不知道被展示的是哪一面的肉餡兒。
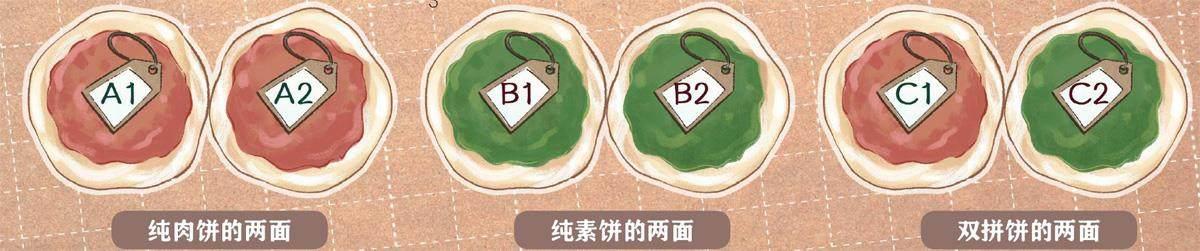
如果這張餅的一面塞的是肉餡兒,共有A1、A2、C1三種可能;而另一面也是肉餡兒則有A2、A1兩種可能。換句話說,當你看到A 1時,背面是A 2;當你看到A 2時,背面是A 1。但當你看到C 1時,背面是C 2。以上三種情況中前兩種都是純肉餅,最后一種是雙拼餅。因此,小問號吃上純肉餅的概率是 ,換算成百分比就是66.666667%。
盡管選擇成功的概率更高,但小問號仍然面臨著選擇失誤(即選中雙拼餅)的“風險”。世界是不斷變化的,許多事情都充滿了不確定性,我們能做的就是努力提高成功的概率;當最終結果不如意時,學會坦然接受——沒準兒雙拼餅的味道會更好!
可怕的例題來了
1.刷餅鐺的幸運兒 難度:★★
小問號和大聰明決定用石頭剪刀布的游戲決定誰去刷餅鐺,并采用7局4勝的規則。已知前三局小問號都輸了,那么第四局他能贏的概率是多少?
2.選擇更好的獎勵 難度:★★★
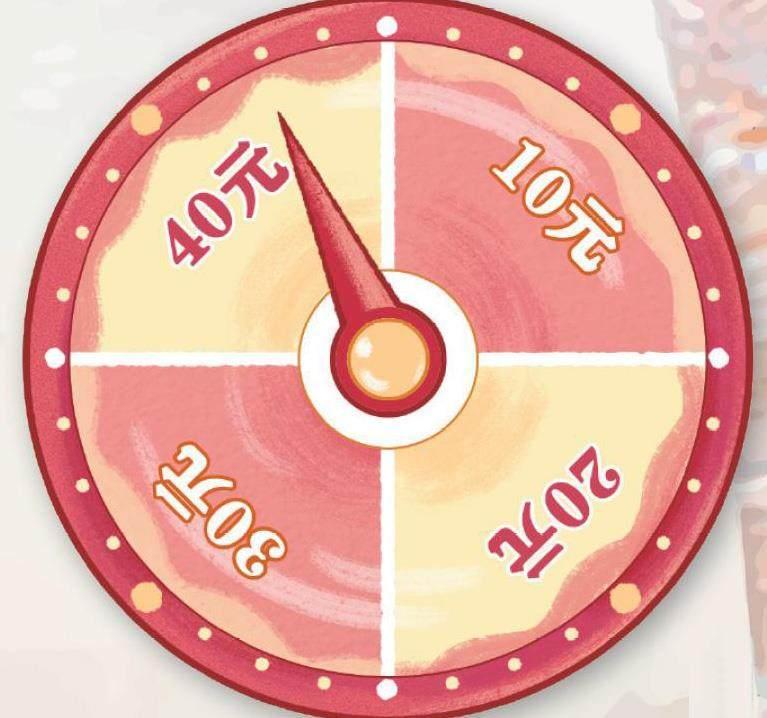
小問號和大聰明在購物后得到一個選擇獎勵的機會:要么直接拿走50元獎金,要么轉兩次轉盤,獲得兩次數額相加的獎金。他們商定,如果轉動轉盤后獲得不低于50元獎金的概率大于50%,那么就參與轉盤游戲。你能算出他們最后有沒有玩轉盤游戲嗎?
猜你喜歡
作文評點報·低幼版(2017年36期)2017-09-11 13:54:17
小火炬·智漫悅讀(2017年4期)2017-06-30 11:10:47
現代家庭·生活版(2017年3期)2017-03-15 18:45:43
學苑創造·A版(2016年11期)2016-12-07 17:28:13
初中生學習·低(2016年10期)2016-11-25 04:51:34
飛碟探索(2016年11期)2016-11-14 19:34:47
作文大王·笑話大王(2016年8期)2016-08-08 11:28:22
小學科學(2015年7期)2015-07-29 22:29:00
小學科學(2015年6期)2015-07-01 14:30:14
小天使·一年級語數英綜合(2014年3期)2014-03-15 01:30:19

