首屆宇宙新星選拔大賽開幕
大力

大賽組委會積極采納群眾意見,值得鼓勵。但說實話,他們提供的兩個方案,我根本沒看出有啥區別呀!
失之毫厘,謬以千里!“推選一個星球”和“各選一個星球”涉及兩種不同的計數原理。
加法原則
加法原則的核心是“分類”。假設事件A有m種產生方式,事件B有n種產生方式,則事件A或B則有m+n種產生方式。
乘法原則
乘法原則的核心是“分步”。完成一件事需要分成2個步驟,做第一步有a種方法,做第二步有b種方法,那么完成這件事共有 a×b 種方法。
我相信你們都聽懂了吧?!
聽懂了才怪……
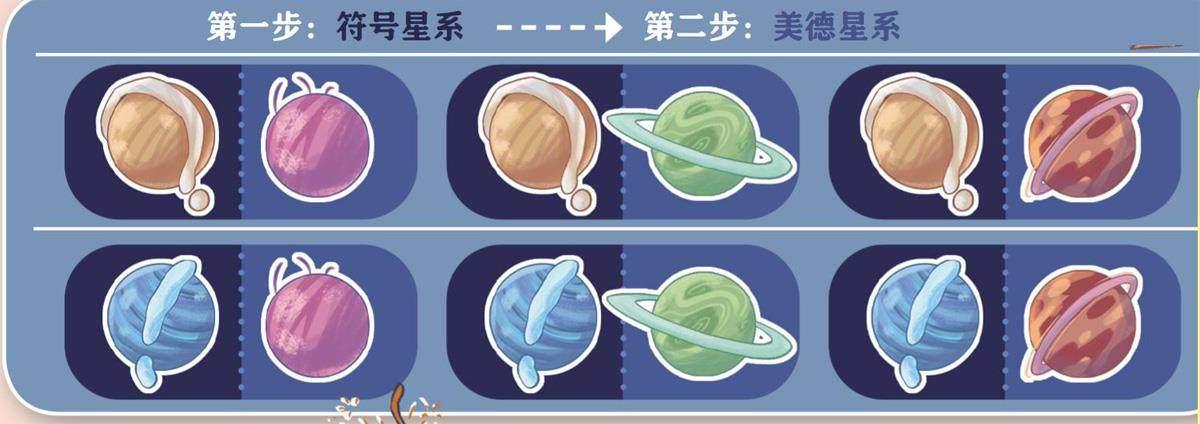
第一種方案是從兩大星系中選取一個星球作為大獎得主。大家要么是從符號星系的2個星球里選,要么是從美德星系的3個星球里選。
大獎得主共有2+3種(即5種)可能,這種方案涉及加法原理。
那第二種方案呢?
第二種方案是從兩大星系中各選一個星球作為大獎得主。大家需要分兩步完成推選,因此會用到乘法原理。大獎得主共有以下6種可能:
畫重點
有個簡單的小技巧來區分兩者,就是看看能不能一次性完成這件事,如果能一次性完成就用加法原則,不能就用乘法原則。
我好像悟到了!
比如我有2件深色外套、3件淺色外套,那么我就有5種選擇方案。我只選1次就行,因此用加法原理。
如果我有2件上衣、3條褲子,那么我就有6種選擇。因為我必須得用上衣搭配褲子,所以要選2次,因此用乘法原理。
孺子可教也!
到了中學,你們會接觸到一個數學術語“排列組合”。我們剛才提到的“加法原理”和“乘法原理”就是排列組合的基礎。
排列是什么呢?簡單來講,就是把事物排在一起,構成一列,計算共有多少種排法。組合呢,就是從整體中選取部分元素進行組合,然后計算有多少種組合方式。
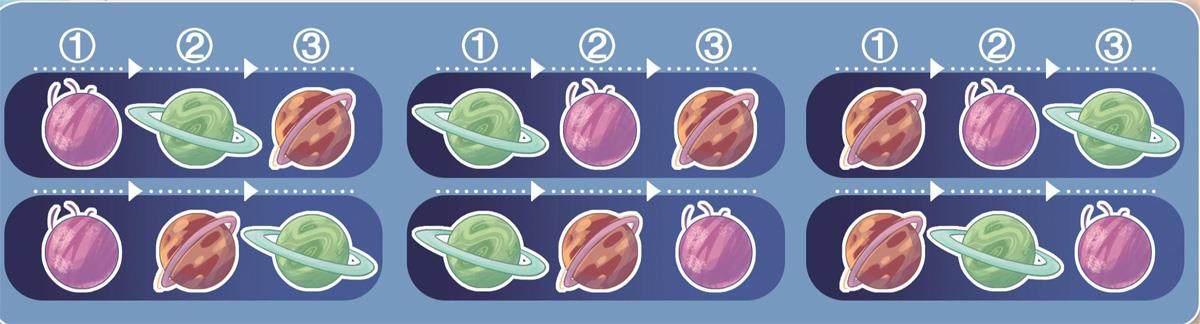
“有順序”和“無順序”是區別二者的重要準則,比如美德星系的組合只有1種,即聰明星球、善良星球和正義星球。但如果排列它們的出場順序,就有6種可能:
很簡單對不對?但我們在日常生活中常常發現更為復雜的情況:我們在做一件事情時,往往有幾類不同的方法,而在每一類方法中,還要分步完成。那么,完成整件事情既要排列又要組合。
問題來了
假設出場節目有10個,分別是5個唱歌節目、3個舞蹈節目、2個相聲節目,且舞蹈節目不能連續出場,那么一共能排出多少種出場順序?
您說慢點兒……
要不我們一個個排?
哈哈哈,我被自己出的題難倒了,還是降低一下難度吧!讓每個星球隨便出一個節目,共有幾種出場順序呢?
解決這一問題我們用到的是乘法原理,出場順序可能性共計5×4×3×2×1=120種。這是一個較為簡單的排列問題。
為了增進宇宙民眾的友誼,我們讓這5個星球兩兩組合表演節目,那么又有多少種組合方式呢?
只要在1次選擇中兩兩配對,就屬于組隊成功,因此我們用到的是加法原理,即有4+3+2+1=10種組隊可能。這是一個較為簡單的組合問題。
可怕的例題來了
1.在排5個星球的節目單時,問號星球和聰明星球作為承辦方,必須出一個星球第一個表演節目,共有幾種排節目單的方法呢?難度:★★★
2.為了更好地展示宇宙的精神面貌,每個星球各派出2名選手參賽。如果讓這10名選手兩兩組合表演節目,那么共有多少種組合方式呢?難度:★★★★

