無人水翼航行器縱向運動建模及控制研究

孫佳宇，劉增武，段富海，毛 翎

(1.大連理工大學 機械工程學院, 遼寧 大連 116024；2.大連測控技術研究所, 遼寧 大連 116013)

0 引 言

無人航行器具備隱蔽性好、體積小以及自主能力強等獨特優勢，可用于海面巡防、反潛、反水雷等任務，已成為海防領域不可或缺的重要力量[1]。現階段國內外無人航行器已進入實用階段，研究重心為如何提高其性能。將水翼應用于無人航行器以提升其整體性能已成為一個新的研究熱點。近年來各種無人水翼航行器相繼出現，如波浪能推進水面航行器[2]、兩棲水翼航行器[3]、無人水翼船[4]等。

T-S 模糊模型是一種非常有效的非線性系統線性化方法[5]，現階段已應用于船舶減搖[6]、動力定位船舶控制[7]、水翼船運動控制[8]等領域，可為無人水翼航行器的數學建模與姿態控制系統的設計提供借鑒。

最優控制中LQR 算法比較成熟，因此廣泛應用于T-S 模糊模型的控制。但LQR 的參數多采用人工試湊的方法進行選取，效率低下且難以選取到最優參數。為改進選取參數的盲目性，可采用布谷鳥算法對LQR參數進行尋優。

本文首先介紹一種新型無人水翼航行器并建立其縱向運動非線性數學模型，利用T-S 模糊模型對非線性數學模型進行線性化；然后對T-S 模糊模型中各子系統設計LQR 控制器，并采用布谷鳥算法對LQR 控制器參數進行優化。最后，通過仿真驗證在隨機海浪干擾下所設計控制器的有效性。

1 無人水翼航行器整體結構及運行機理

無人水翼航行器結構如圖1所示，其動力源為兩電機帶動螺旋槳轉動在水中產生推力推動航行器前進。初始狀態下僅航體漂浮在水面上，其余部分均浸沒在水中，隨著運行速度提高，水翼升力也隨之變大，當達到一定速度后水翼升力可將航體抬出水面達到翼航狀態。翼航狀態下可通過調整前后水翼轉動角度以改變前后水翼升力大小，進而可以調整航行器姿態。航行器姿態控制系統如圖2 所示。

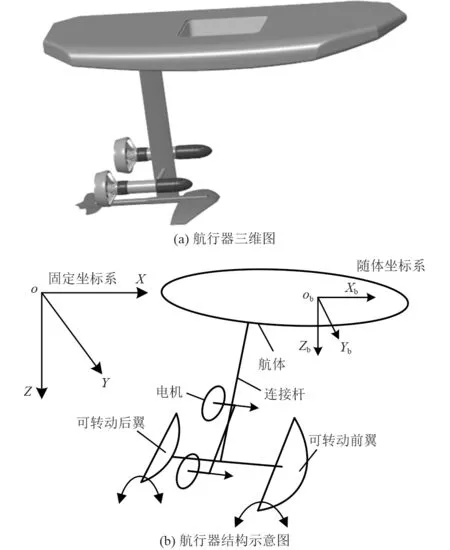
圖1 無人水翼航行器示意圖Fig.1 Schematic diagram of unmanned hydrofoil vehicle

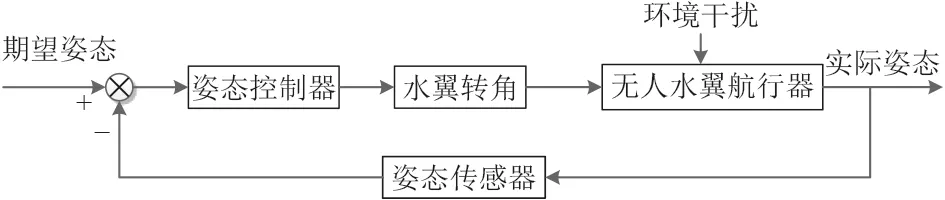
圖2 航行器姿態控制系統示意圖Fig.2 Schematic diagram of vehicle attitude control system

2 無人水翼航行器縱向運動數學模型

2.1 非線性數學模型的建立

無人水翼航行器運行機理與水翼船相似，因此可借鑒文獻[8]水翼船數學模型對其進行建模。考慮航行器縱傾和波浪對航行器運動的影響，忽略海流、海風等其他因素。翼航狀態下航行器縱向受力如圖3 所示。

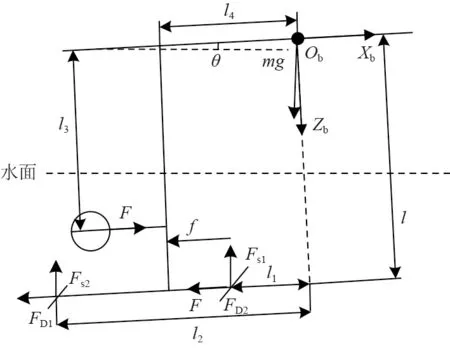
圖3 翼航狀態下航行器縱向受力示意圖Fig.3 Longitudinal force diagram of vehicle under wing navigation

Fsi為前后水翼產生的升力與慣性力的合力(i=1 為前翼，i=2 為后翼)，即Fsi=Lfi+Fai。li為水翼距航行器重心距離。水翼升力Lfi的計算公式為：

式中：ρ為水密度，1 000 kg/m3；v為航行器運行速度；Si為水翼投影面積，Si=Libi；Li為水翼展長，bi為水翼弦長；Cfi為水翼升力系數，在文獻[9]中有詳細計算過程，水翼升力系數可近似看作與攻角成線性關系[10]。攻角計算公式為：

式中：αsi為水翼旋轉角度，在±15°內變化；θ為縱搖角；ξ為航行器垂直于水平面升沉量；ζi為次波面海浪波形；α0i為水翼零升力攻角。

當航行器在水中運動時，會受到其周圍流體作用的慣性力Fai，其計算公式為：

FDi為水翼阻力，其值遠小于水翼升力[8]，所以忽略其在Zb軸方向分量，近似其方向與Xb軸平行，其計算公式為：

式中，CDi為水翼阻力系數，詳細計算過程見文獻[9]。

f為連接桿割劃水面所產生的阻力，將連接桿抽象成一細長圓柱體，根據Morison 公式，作用在靜水中勻速運動長度為dz的圓柱切片上的水平阻力大小為：

式中：D為圓柱直徑，取為0.05m；Cd為阻力系數，取為1。連接桿水下浸沒深度為h時的阻力大小為：

縱傾角小范圍內變化時h≈l+ξ+l4θ，l4為連接桿至重心距離。

而阻力的力矩則可由下式計算：

設F為電機推力，勻速運動時與阻力大小相同，l3為電機推力力臂。在Zb方向利用牛頓第二定律并以Yb為轉軸利用剛體定軸轉動定律，可得到航行器翼航狀態下縱向垂蕩和縱搖運動數學模型：

無人水翼航行器結構參數如表1 所示。

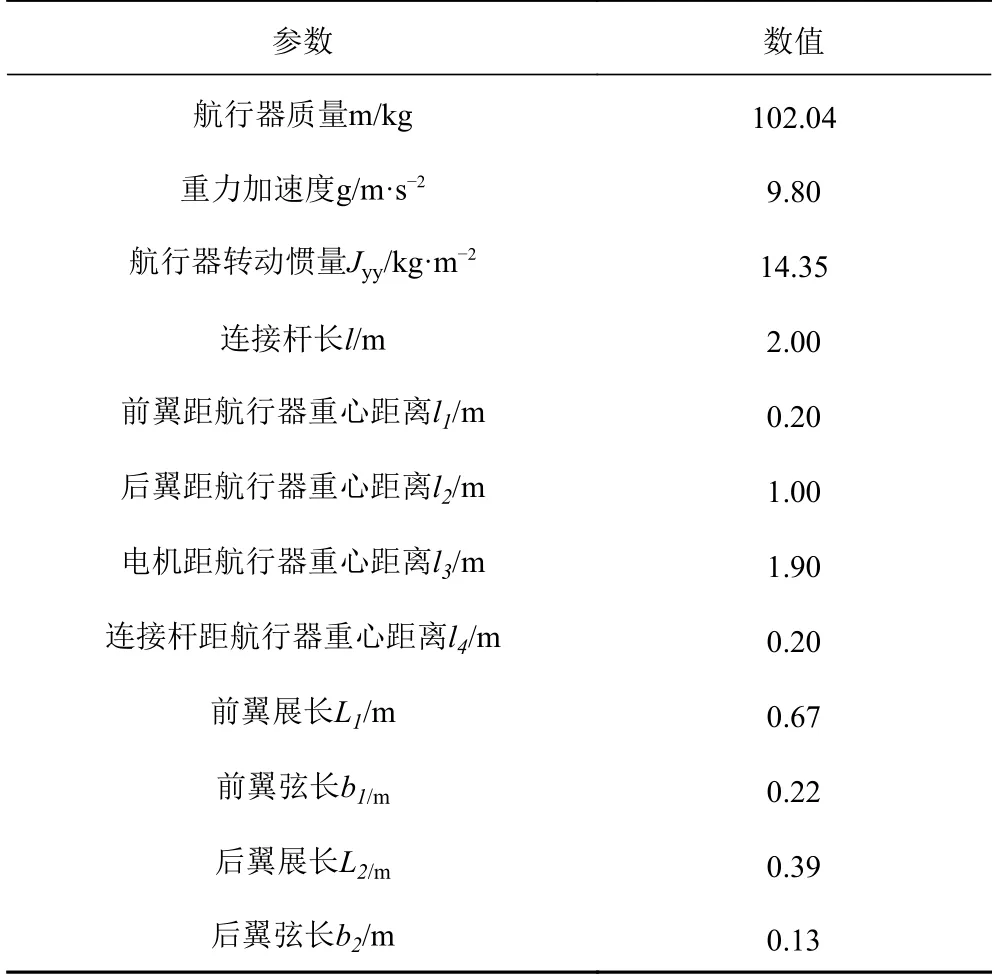
表1 無人水翼航行器結構參數Tab.1 Structural parameters of unmanned hydrofoil vehicle

2.2 航行器T-S 模糊模型的建立

T-S 模糊模型的主要思想是將復雜非線性曲線用多條線段進行擬合，進而將非線性問題轉化為多條小線段上的線性問題。航行器縱向運動T-S 模糊模型前提變量選取縱搖角θ，設航行器翼航狀態時縱搖角范圍為0°～4°，則前提變量分別取縱搖角θ為0°、2°、4°，由式(8) 可得各子系統參數如表2 所示。模糊規則如下：

在子系統1 工作點對式(8)進行線性化，即可得到如下參數：

其余A2，A3；B2，B3；H2，H3類似。

T-S 模糊模型的總輸出為：

式中，wi為第i條規則關于縱傾角的隸屬度函數，為三角形隸屬函數，如圖4 所示。

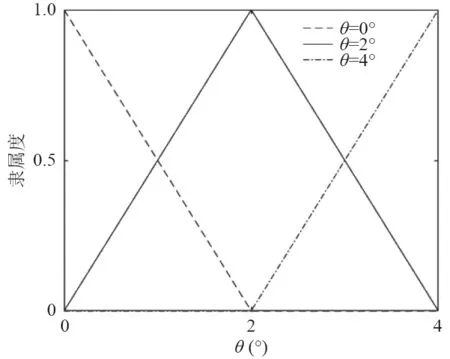
圖4 隸屬度函數Fig.4 Membership Function

并行分布補償法(PDC)適用于解決基于T-S 模糊建模的非線性系統控制問題[11]。采用PDC 方法設計的T-S 模糊控制器為：

式中，Ki為各子系統反饋增益矩陣。

3 LQR 控制器設計及優化

3.1 LQR 控制器

LQR 算法核心是用最小輸入代價實現對各個目標的有效控制，狀態空間方程為：

LQR 控制就是要尋找一個最優控制矩陣K，即確定一個狀態反饋控制率u(t)=Kx(t)，使得如式(13)所示的性能指標達到最小。

反饋增益矩陣為：

矩陣P可由黎卡堤方程求得：

LQR 控制器控制性能的好壞直接與Q矩陣與R矩陣的取值相關，因此Q矩陣與R矩陣的選取是LQR 控制器設計的核心內容。

3.2 布谷鳥算法

布谷鳥搜索（CS）算法是由Yang 和Deb 于2009 年提出的一種智能優算法[12]。CS 算法采用下式對下一代鳥巢位置進行更新：

CS 算法首先由式(16)對下一代鳥巢位置更新，如果適應度函數值優于上一代則更新鳥巢位置。位置更新后每個鳥巢的位置有Pa的概率會再次隨機改變位置，然后保留測試值最好的一組鳥巢位置，記為。最后判斷算法是否滿足結束條件，若滿足，則結束迭代尋優，輸出全局最優值。

3.3 基于布谷鳥算法的LQR 控制器優化設計

利用CS 算法對LQR 控制器進行尋優。首先確定Q和R矩陣所需尋優參數的個數，確定CS 算法中搜索空間的維數和鳥巢坐標與各參數的對應關系，每個鳥巢即為各參數的集合體，本文設定Q矩陣形式為：

式中：q1和q3均取為0，僅調整q2和q4，R矩陣取為單位矩陣。

鳥巢的好壞由適應度函數所決定，采用時間誤差積分準則（ITAE）作為適應度函數，以確保系統具有良好的動態性能[13]。CS 算法的目標就是找到一個最優鳥巢，然后將尋優后的參數代入Q矩陣得到最優Q矩陣，計算后得到最優狀態反饋K矩陣。具體流程圖如圖5 所示。

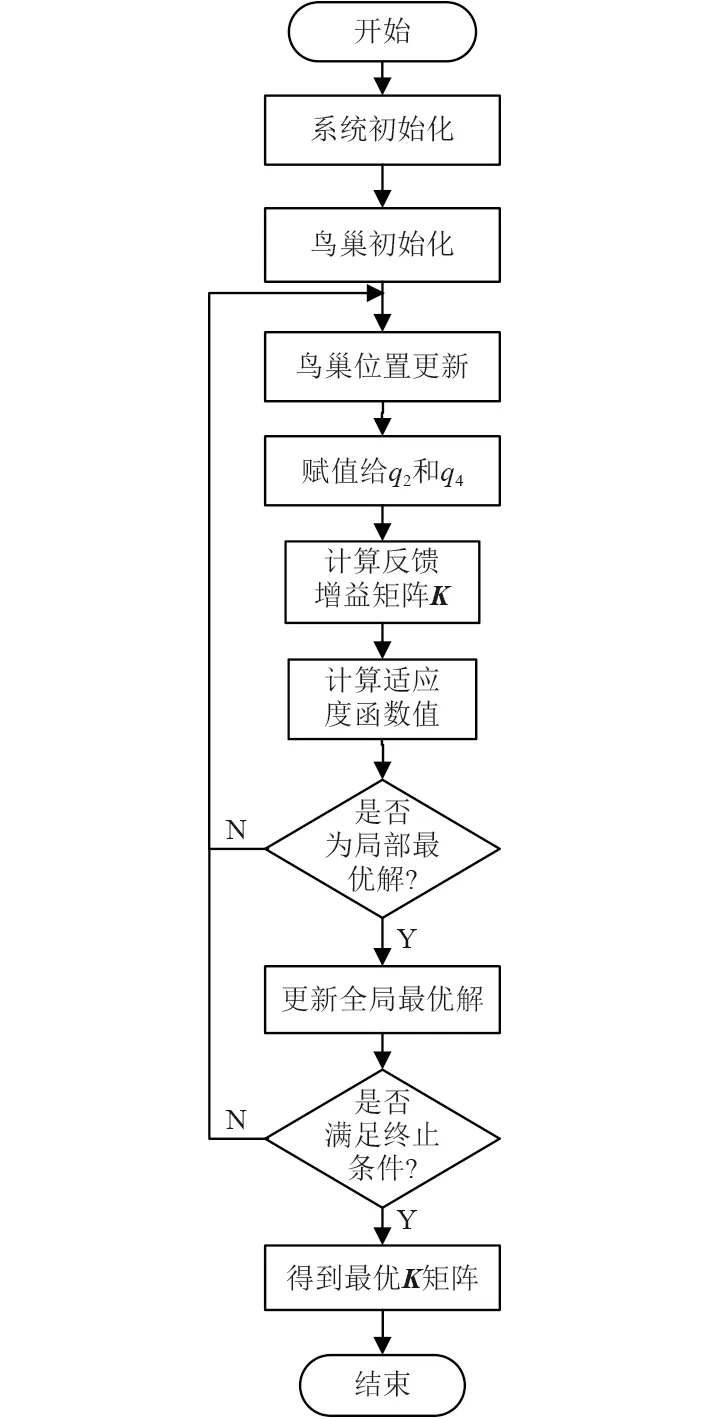
圖5 布谷鳥算法優化LQR 流程圖Fig.5 LQR flow chart of cs algorithm optimization

4 仿真及結果分析

利用CS 算法對3 個子系統進行LQR 控制器參數整定，算法初始參數設置為：鳥巢數量為10、步長控制量α=1、發現概率Pa=0.25、變量取值下界為[0,0]、變量取值上界為[5 000,5 000]，迭代次數100 次，最終得到各子系統反饋增益矩陣為：

為檢驗CS 算法優化LQR 縱向姿態控制器的性能，加入隨機海浪干擾，海浪參數為有義波高1 m，遭遇角120°，利用Matlab 2020b 軟件編寫程序，取縱搖角θ為1°，2°，3°三個工作點進行仿真。以升沉量誤差Δξ和縱搖角誤差Δθ作為評定縱向姿態控制器性能的指標，仿真結果如圖6～圖8 所示。

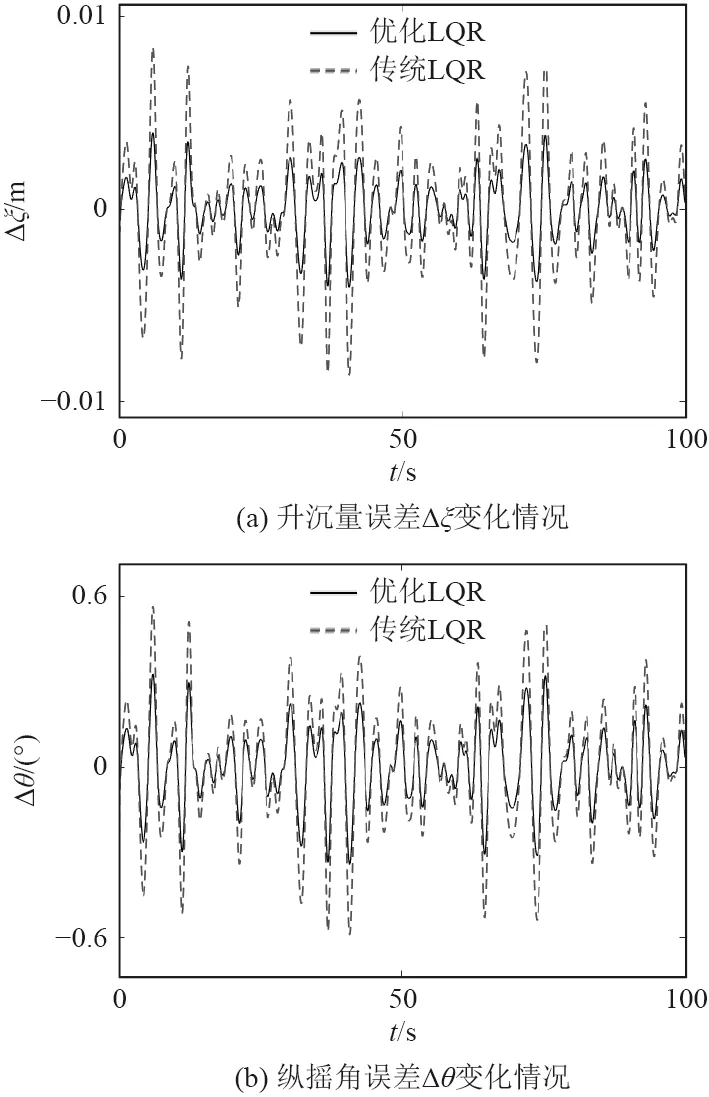
圖6 縱搖角1°時控制效果Fig.6 Control effect at pitch angle of 1°

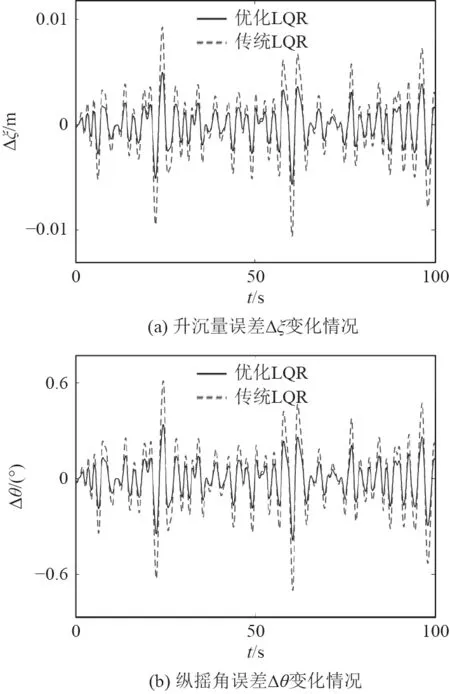
圖7 縱搖角2°時控制效果Fig.7 Control effect at pitch angle of 2°

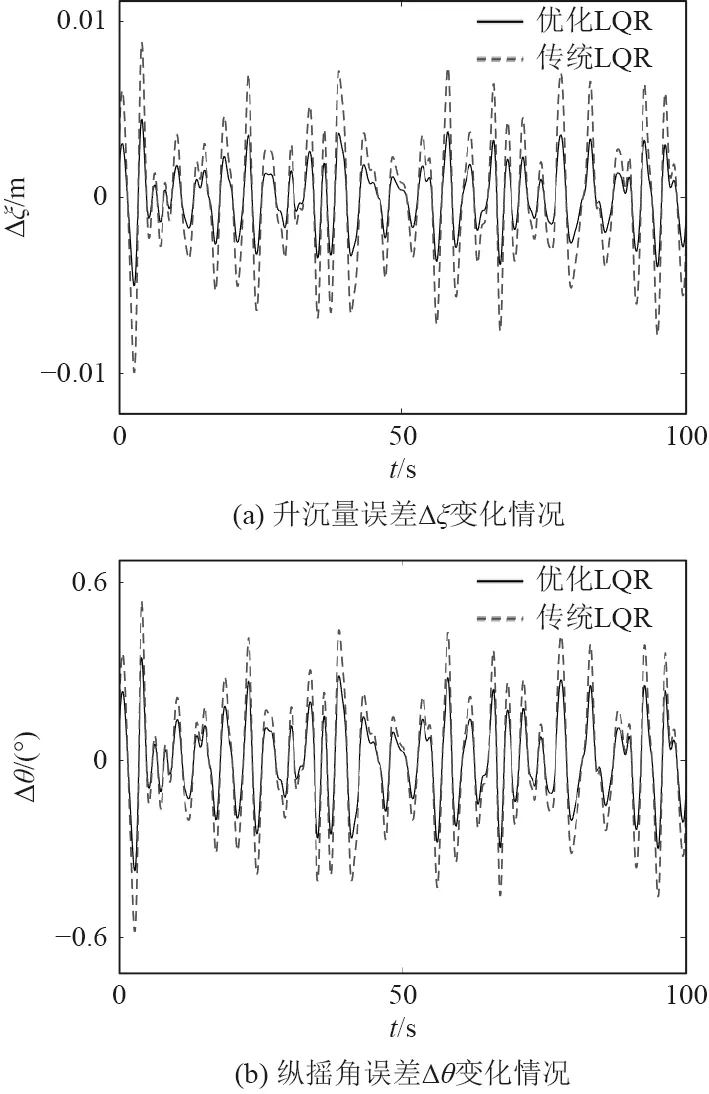
圖8 縱搖角3°時控制效果Fig.8 Control effect at pitch angle of 3°

由仿真結果可見在隨機海浪干擾下LQR 控制器對航行器縱向運動姿態具有良好的控制性能，升沉量誤差Δξ和縱搖角誤差Δθ均控制在小范圍內，且利用CS 算法設計LQR 控制器不僅避免了人工試湊法的繁雜過程，控制效果也優于傳統LQR 控制器。

5 結 語

本文提出一種新型無人水翼航行器，并以水翼船模型為參考對其進行縱向運動建模和T-S 模糊模型線性化。設計LQR 控制器，針對LQR 控制器采用人工試湊法調節參數效率低下的問題，利用布谷鳥算法對控制器進行優化。通過仿真驗證了LQR 控制器對航行器在海浪干擾下的縱向姿態具有良好的控制效果，且經過布谷鳥算法優化后的LQR 控制器控制效果優于傳統LQR 控制器。本文研究可為新型無人水翼航行器的實體樣機設計提供理論依據，也可為其他種類航行器設計提供借鑒。