步步為營 分分必爭
文/高戈爾
函數是初中數學的重要內容,也是中考數學必考題型。函數問題頗具抽象性和復雜性,同學們常常“會而不對,對而不全”,如何突破這一難關,做到“會便對,對求優”?下面就以一道2022 年無錫市中考題(滿分10 分)為例加以分析,供同學們復習參考。
某農場計劃建造一個矩形養殖場,為充分利用現有資源,該矩形養殖場一面靠墻(墻的長度為10m),另外三面用柵欄圍成,中間再用柵欄把它分成兩個面積為1∶2 的矩形,已知柵欄的總長度為24m,設較小矩形的寬為xm(如圖1)。
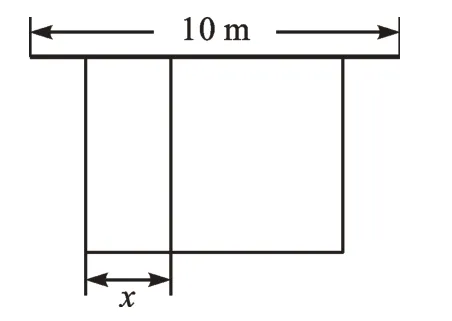
圖1
(1)若矩形養殖場的總面積為36m2,求此時x的值;
(2)當x為多少時,矩形養殖場的總面積最大?最大值為多少?
解:(1)根據題意,得
化簡,得x2-8x+12=0。(2分)
解這個方程,得x1=2,x2=6。(4分)
經檢驗,當x=6 時,3x=18>10,不符合題意,應舍去。
∴x=2。
答:此時x的值為2m。(5分)
(2)設矩形養殖場的總面積是ym2。
根據題意,得y=-3x2+24x=-3(x-4)2+48。(7分)
由二次函數圖像與性質可知,當x<4時,y隨x的增大而增大。(8分)
【踩點得分提示】從評分標準可以看出:第(1)問,正確列出方程2 分,解方程正確2分(每個解1分),由自變量取值范圍取舍解1分;第(2)問,列函數表達式正確2 分,闡述二次函數增減性1分,求出最大值1分,答1分。
扣分點一:第(1)問中,題設中養殖場中間含柵欄,表示矩形長時要用總材料減去3段寬。審題出錯,滿盤皆輸,所以準確審題是邁向“成功”的第一步。
扣分點二:第(1)問中,墻面長度為10m,所以3x≤10,故x=6 不合題意應舍去。以實際問題為背景,不能忽視實際情況的“約束”。
扣分點三:第(2)問中,因為,所以無法在頂點處取得最值,可結合函數圖像利用函數增減性考慮問題。因此,用二次函數模型解決實際問題,需關注自變量的取值范圍對函數最值產生的影響。

