提煉解題模型 提高解題技能
文/李進

三角形是中考必考圖形。從問題中提煉模型,可以幫助我們分析解題,也是我們需要培養的重要技能之一。下面,我們對一道中考題進行分析,解讀掌握模型的重要性。
(2022·湖南湘潭)在△ABC中,∠BAC=90°,AB=AC,直線l經過點A,過點B、C分別作l的垂線,垂足分別為點D、E。
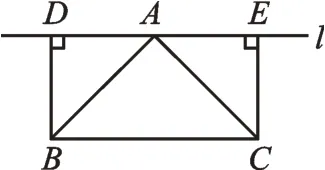
圖1
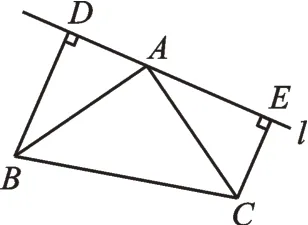
圖2

圖3
(1)特例體驗:如圖1,若直線l∥BC,AB=AC=,分別求出線段BD、CE和DE的長;
(2)規律探究:
(Ⅰ)如圖2,若直線l從圖1 狀態開始繞點A旋轉α(0<α<45°),請探究線段BD、CE和DE的數量關系并說明理由;
(3)根據題意,我們容易證明△ABD∽△FBA,由此可得出BF的長,從而根據S△BFC=S△ABC-S△ABF得出結論。
2016年,美國疼痛學會、美國麻醉科醫師學會和美國區域阻滯與疼痛醫學學會聯合發布了術后疼痛管理指南[1],提出多模式鎮痛作為圍術期疼痛管理的核心。該指南在術后疼痛管理的多方面均作出了更新,要求麻醉科醫師進一步改進臨床行為,將單一的以術后鎮痛藥物作為疼痛管理的方式改進為基于“藥物干預-局部阻滯技術-區域阻滯技術-椎管內鎮痛-非藥物手段干預”等技術手段的多模式鎮痛,以不斷完善術后鎮痛的質量和療效。針對中國的現狀,主要有以下三點需要作出改進。
【分析】(1)容易證明△ABD和△ACE均是等腰直角三角形,然后根據等腰直角三角形的三邊關系可得到BD、CE和DE的長。
(Ⅱ)容易證明∠ABD=∠CAE,由“AAS”即可得出△ABD≌△CAE,從而解答;
(3)嘗試應用:在圖3 中,延長線段BD交線段AC于點F,若CE=3,DE=1,求S△BFC。
(2)(Ⅰ)容易證明∠ABD=∠CAE,由“AAS”即可得出△ABD≌△CAE,從而解答;
(Ⅱ)如圖3,若直線l從圖1 狀態開始繞點A順時針旋轉α(45°<α<90°),與線段BC相交于點H,請再探線段BD、CE和DE的數量關系并說明理由;
解:(1)在△ABC中,∠BAC=90°,AB=AC,
2.2.2治理原理采用工程措施修整侵蝕溝溝體,布設植物防護體系,恢復生態,穩固溝體。當侵蝕溝坡度較大或者溝體不適宜種植植物時,采取工程措施(削坡、魚鱗坑、水平階等)對侵蝕溝做溝形修飾,從而確保植物措施的實施、成活與生長,發揮固溝導水作用。
正是豐收時節的一天,我在路上遇到二叔,想到他家種了四畝葡萄,便笑著問:“二叔,今年數錢都數到手酸了吧?”我本想二叔一定會微笑著謙虛地說“哪里哪里,除了鍋巴不剩飯”,可他苦笑了一下,嘆口氣說:“白苦一年不說,還倒貼黃瓜二條,貼老本了。”
在Rt△ADB中,∠ABD+∠BAD=90°。
匱乏組織化的機構是一個非常現實的問題。但是,中國的家庭承擔了主要責任,而且幾乎每個人在相當大程度上都擁有自己的“親朋好友”。通過慈善基金和一般性捐贈,我們建立了一個救助備用基金,以便為那些亟需金錢的患者提供救助。許多病人不需要或只需要極少量的金錢,他們迫切需要的是醫療人員的專業知識,迫切需要知道如何讓病人和他們的家人獲得所需醫療信息的方式,迫切需要知道社區能夠提供什么,迫切需要知道他們能夠做什么和他們應該怎樣做。
在△ABD和△CAE中,
(2)(Ⅰ)DE=BD+CE。理由如下:
1962年1月天津市五一表廠更名為“天津手表廠”,同年底工廠遷入復康路新址,其工裝設備、生產規模和產品數量都得到了提升。早在1961年3月天津表廠技術人員張鳳鳴、溫淑杰、江達生等設計出一款帶秒表測時機構的計時碼表機心,表廠定型為“ST3型”。到1963年12月表廠試制出該機心航空計時表樣機32只,并通過輕工部和部隊主管部門專家組的鑒定,該表定名為“304”航空表,是我國第一款裝備空軍飛行員的航空計時表(圖09)。
(Ⅱ)DE=BD-CE。理由如下:
在Rt△ADB中,∠ABD+∠BAD=90°。
在△ABD和△CAE中,
(3)由(2)可知,∠ABD=∠CAE,DE=AEAD=BD-CE。
教師在開展中長跑運動時,單一的以訓練為主,沒有合適的方式方法,無法引導學生去擺脫抵觸情緒,所以學生的畏難心理日益嚴重,對中長跑運動的興趣也直線下降。
【點評】本題是一道三角形綜合題,考查了直角三角形的性質、全等三角形的判定與性質、相似三角形的性質與判定、三角形的面積等知識。
在解答本題時,我們主要運用了“一線三等角”模型:指有三個等角的頂點在同一直線上的構圖。“一線三等角”模型中的三角形分在直線同側和異側兩類,角分直角、銳角、鈍角三種,如圖4。在這樣的模型中,我們容易找到一對全等三角形或一對相似三角形,即△ABC與△CDE全等或△ABC與△CDE相似,從而為下一步解決問題提供思路。
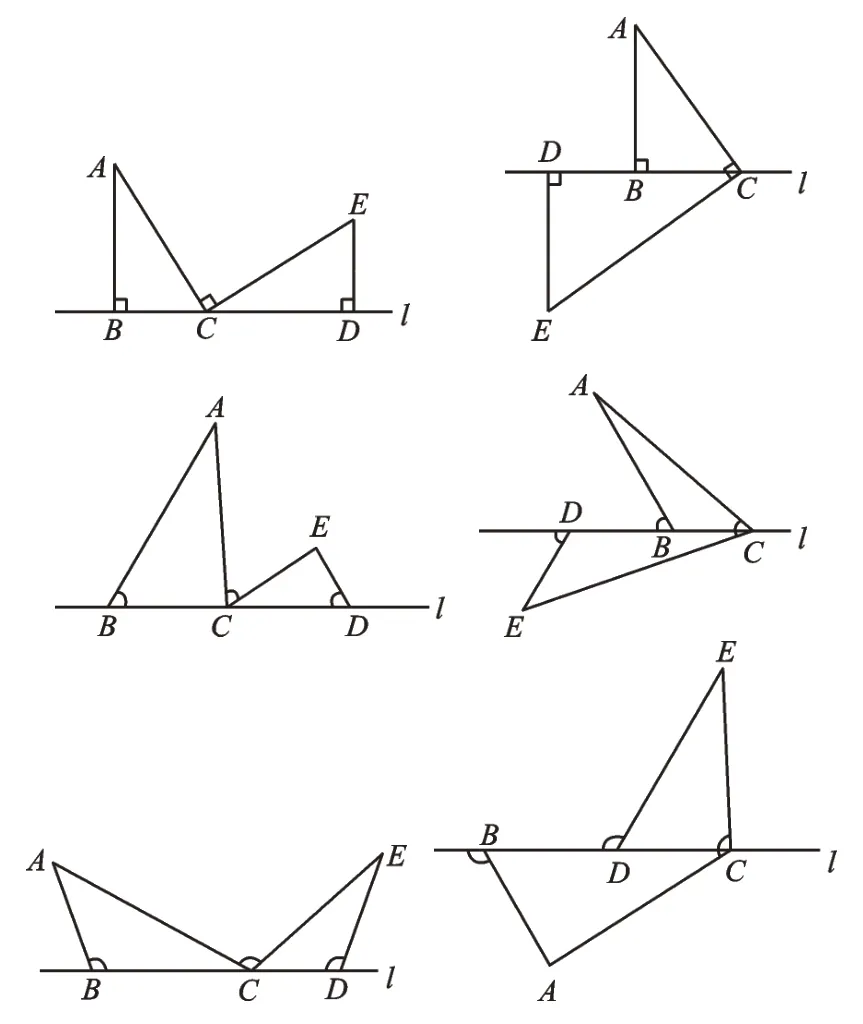
圖4

