思維培育有方法 數學模型記心間

文／王磊

從學習數學的時間軸上看，通透了解數學模型，深度掌握解題方法，有效培養數學思維，遠比會解一道題重要得多。下面，我們通過幾道例題，感受與三角形有關的四種數學模型。

一、“手拉手”模型的解題策略

“手拉手”模型的典型特征是兩個三角形的一個頂點相互重合，通過旋轉等圖形變化后，可形成一些結論和規律。

例1如圖1，在△ABC中，AB=CB，∠ABC=90°。D為AB延長線上的一點，點E在邊BC上，連接AE、DE、DC，AE=CD。

求證：∠BAE=∠BCD。

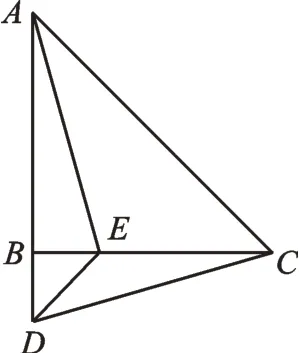
圖1

【解析】本題中，要證明∠BAE=∠BCD，我們只需證明出△ABE≌△CBD即可。題干已經告訴我們AB=CB、AE=CD、∠ABC=90°這三個條件，我們可以通過“HL”來證明。

其實，該模型可以探究的地方還有很多。比如AE與CD的位置關系（提示：AE⊥CD），這也是考試中常遇到的問題。同學們可以試著猜想和證明一下。

二、“動點”問題的解題策略

“動點”問題的難點就在于點位置的靈活性。遇到這類問題，只要根據“軸對稱的性質”“兩點之間，線段最短”等知識，將動態轉變為靜態，就可巧妙地解決這類問題。

例2如圖2，在等邊三角形ABC中，AB=4，P是BC邊上的動點，Q是BA邊上的動點，H是AC邊上的動點，則△PQH周長的最小值為________。

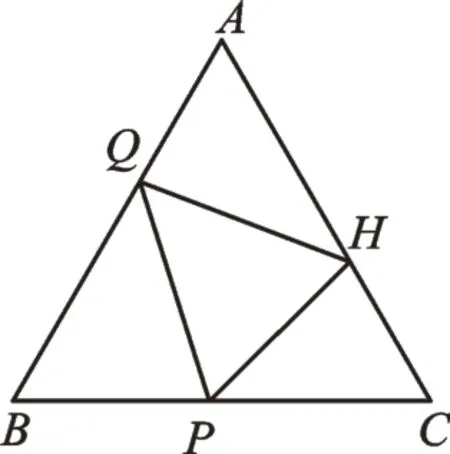
圖2

【解析】△PQH三條邊的長度在不斷變化，這給我們的解題帶來了極大的困難。我們可以作點P關于AB的對稱點M，以及點P關于AC的對稱點N，如圖3，則根據軸對稱的性質，得到QP=QM，HP=HN。根據“等量代換”，得QP+PH+QH=QM+QH+HN。連接MN，根據公理“兩點之間，線段最短”，可知QM+QH+HN的最小值就是線段MN的長，所以△PQH周長的最小值為MN。當點P為BC的中點時，MN最小，MN=BC=6。

圖3

三、“一線三等角”問題的解題策略

“一線三等角”問題的特征是在一條線的同側或異側，有兩個全等或相似的三角形。在這樣的組合圖形中，蘊含了成比例、相等、互余等關系。

例3如圖4，E是正方形ABCD的邊AB上的動點，EF⊥DE交BC于點F。

（1）求證：△ADE∽△BEF。

（2）設正方形的邊長為4，AE=x，BF=y。當x取什么值時，y有最大值？并求出這個最大值。

圖4

【解析】（1）要證相似的這兩個三角形中，已知的條件有∠DAE=∠EBF=90°，那么只要得出另外一組對應角相等即可。因為∠ADE+∠DEA=90°，而∠AED+∠FEB=90°，所以∠ADE=∠FEB，如此就滿足了兩個三角形相似的條件。在（2）中，可用x表示出BE的長，然后根據（1）中△ADE∽△BEF可得出比例關系式，然后就能得出一個關于x、y的函數表達式。根據函數的性質即可得出當x=2時，y有最大值，最大值為1。

四、“瓜豆”問題的解題策略

“瓜豆”問題的特征就是一個主動點，一個從動點。從動點受到某種條件的約束，跟著主動點動。當主動點發生運動時，從動點的軌跡與主動點的軌跡相同或相似，且運動軌跡長度的比和它們到定點的距離比相同。

例4如圖5，△ABC中，∠ACB=90°，CA=CB=4，CD⊥AB于點D，P是CD上一個動點，以P為直角頂點向下作等腰直角△PBE，連接DE，求DE的最小值。

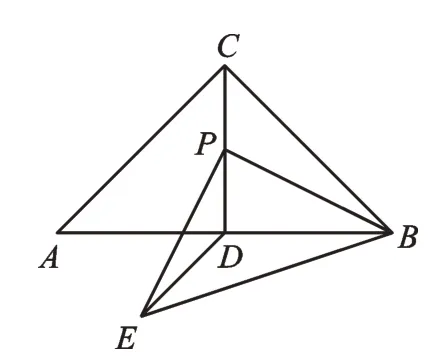
圖5

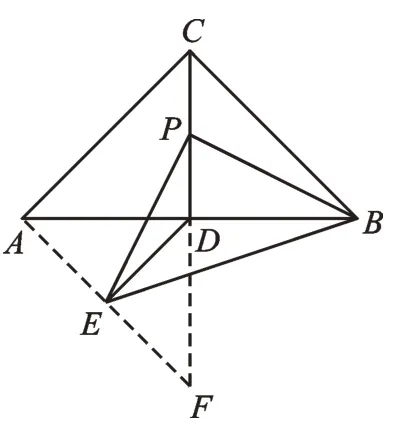
圖6

【解析】通過觀察和推理，我們可以發現，點E的運動軌跡是一條線段，也就是圖6的AF。當點P在C點時，點E在A點；當點P到達D點時，點E在D的下方，且長度等于CD。因此，DE的最小值就是Rt△ADF斜邊上的高，DE的最小值為2。