城市快速路互通立交交織區長度可靠性設計

張 航,段和柱,儲澤宇

(武漢理工大學 交通學院,湖北 武漢 430063)

0 引 言

互通立交交織區作為城市快速路系統的重要組成部分,是發揮交通功能的瓶頸區以及交通事故的多發區。當城市快速路互通立交的匝道出入口間距不能滿足規范要求時,通常需要在相鄰入口和出口間增設輔助車道,互通立交區域內的車輛會在輔助車道及相鄰車道間發生交織行為,這要求該輔助車道最小長度應符合車輛完成車道變更行為所需要的距離(即該輔助車道的長度需要滿足交織區的長度),并與城市快速路整體的道路通行能力相適應。若交織區長度過小,會嚴重影響城市快速路的道路通行能力,甚至造成交通事故;若交織區長度過大,雖然可以提高互通立交整體的通行效率,但會導致占地面積大且工程造價更高。因此,應從交通安全、道路通行能力等角度綜合考慮來確定合理的交織區長度。

目前,學者對城市快速路交織區內的通行能力以及交織區長度廣泛的研究。周榮貴等[1]通過對國內城市快速路交織區通行能力的研究分析,并借鑒和吸收美國HCM2010交織區運行分析方法的相關規定,出版了《公路通行能力手冊》(簡稱《手冊》);周晨靜等[2]以實測數據為基礎對《手冊》中交織區內的速度計算模型進行了適用性分析,發現模型在城市快速路中同側交織區擬合度較高。上述研究發現,《手冊》中借鑒美國HCM2010交織區的相關方法進行參數標定和修正所用的實測數據均來自城市快速路交織區,因此《手冊》中交織區的相關分析方法普遍適用于城市快速路交織區,但當城市快速路交織區出現過飽和交通流、交織區限速、交織區應用智能交通系統、下游堵塞或需求匱乏、多重交織區等情況時,《手冊》中交織區的相關方法將不再適用。

孟祥燕[3]把交織區長度作為通行能力的主要影響因素,建立交織區通行能力線性優化模型,得出不同交織區長度時對應的通行能力值;徐艷等[4]通過建立以密度為指標評價交織區服務水平計算模型,得到滿足某一服務水平和交織流量下所需的最小交織區長度。這些研究均是基于實例進行分析,得到滿足某服務水平下交織區長度和交織區總流量之間關系,從而得出相應的交織區長度。在研究交織區高效運行、相關道路指標取值滿足規范的同時,該道路指標是否能保證其設計安全,且安全水平有多高,在現階段所有規范中均未具體的說明且缺少直接方法確定交織區長度。特別是交織區長度在CJJ 37—2012《城市道路工程設計規范》[5](簡稱《規范》)中只給出相對范圍(150～750 m),對相應設計速度下的交織區長度未給出明確值,因此當受到道路條件限制,設計人員往往憑經驗確定交織區長度時,其設計指標的預期安全效果將會不太明確。F.P.D.NAVIN等[6]最先將可靠性理論引入到道路工程中去,并采用相關案例進行說明。游克思等[7]通過構建基于質點模型的側滑失效功能函數,評價了車輛在曲線段的安全可靠性。仉文崗等[8]運用可靠度理論相關知識對隧道的施工過程以及運營過程展開分析。

鑒于此,筆者將結合可靠度理論知識,對交織區長度進行安全可靠性分析,采用可靠度指標和失效概率將交織區長度安全可靠性進行量化研究。同時基于現有研究成果及《手冊》交織區中的相關方法,構建交織區長度計算模型;結合可靠度理論知識,依托交織區長度計算模型,建立可靠度功能函數;在不同設計速度下用該函數檢驗《規范》中最小交織區長度的可靠性;并用可靠度指標和失效概率對該指標進行評價;在滿足三級服務水平的條件下,根據城市快速路所采用的目標可靠指標,反算得出不同設計速度下相對應的交織區長度推薦值。

1 互通立交交織區長度確定

1.1 互通立交交織區安全分析

A型交織區是我國城市快速路互通立交中最為典型交織構型如圖1,其中A型交織區主要分布在互通立體交叉中的苜蓿葉立交、環形立交的匝道出入口間及快速路主輔路的出入口間。根據《手冊》中對A型交織區的分析,駕駛員為到達期望車道至少需進行一次車道變更行為[5]。在A型交織區內,交織車輛的車速、道路通行能力及安全可靠性均會隨交織區長度增加而提高。在交織區總流量及交織流量比一定的條件下,主線為雙向四車道的交織區內可實現路徑變更的車道數最少,其道路通行能力也最差[5]。因此,A型交織區內,在主線車道設計為單向兩車道,輔助車道為單車道(即交織區內可用的交織車道數為3的情況下)這種最不利的條件下,計算所得到的交織區長度在應用時最為安全。

圖1 A型交織區

根據《規范》可知,當主線設計速度為100 km/h時,在交織區總流量以及交織流量比相同的情況下,其滿足所需服務水平的交織區長度最長,這表明設計速度越大,越不利于交織車輛完成變更路徑行為,所需的交織區長度越長。根據實地調查數據,交織車道數為3的A型交織區的最大交織流量比為0.45。由《規范》可知,城市快速路基本路段交通安全、順暢行駛的要求是滿足三級服務水平,由于《規范》中未對交織區的服務水平和交通密度做出特殊規定,因此交織區內服務水平標準也采用三級服務水平(采用三級服務水平上限值進行研究,即每車道車流密度為32.0 pcu/km),這樣做也是偏于安全的。則可根據在滿足三級服務水平的條件下,可求得交織區中最大服務交通量,結果見表1。

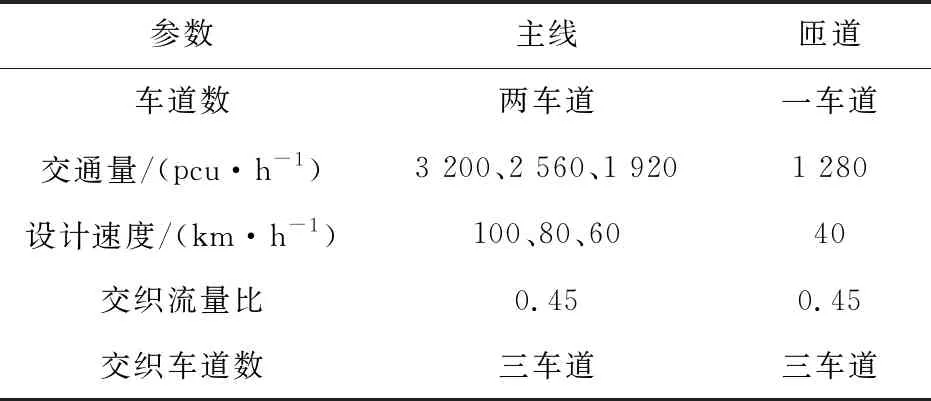
表1 互通立交交織區基本數據設定

1.2 城市快速路交織區長度計算模型

《規范》中規定交織區長度為150～750 m。規范認為,在城市快速路系統中若交織區長度低于150 m,此情況與無信號交叉口類似,可視為無信號交叉口做出研究分析;若交織區長度高于750 m,此情況下車輛有足夠機會去完成交織所需的車道變更行為,相當于一般路段變更車道現象,與基本路段無明顯差別。筆者研究了《規范》中所提供的最小交織區長度在道路設計中的安全可靠性,并在給定服務水平條件下,反算出不同設計速度下相對應的一個交織區長度推薦值,供在城市快速路互通立交確定合理的交織區長度設計進行參考。圖2為城市快速路互通立交交織區長度計算流程。

結合我國城市快速路實際情況,將道路服務水平(車流密度指標)作為約束條件,在上述分析最不利的情況下構建出交織區長度計算模型,利用MATLAB進行腳本代碼的編寫來實現該模型的計算。具體建模思路為:

根據《手冊》交織區相關公式,推導出交織區長度的計算公式,在三級服務水平的條件下,求得該交織區內的最大交通流量,輸入A型交織區最不利交通參數,得到對應于某一車流密度下的交織區長度。

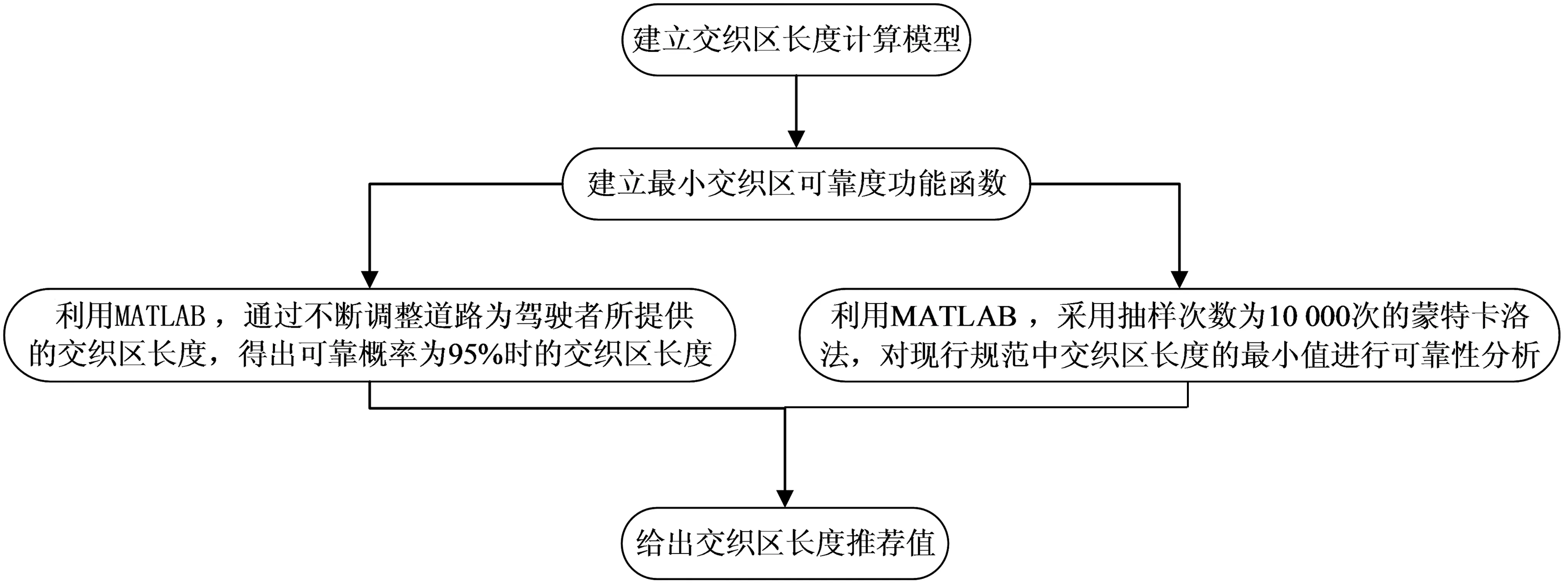
圖2 城市快速路交織區長度計算流程

根據以上思路,城市快速路交織區長度的計算模型如下:

1)交織強度系數Wi

(1)

式中:Q為交織區總流量,pcu/h;Qr為流量比;L為交織區長度,m;N為交織區內總車道數;a、b、c、d為標定的常數,可參照《手冊》,如表2;Q為交織區總流量,pcu/h。

當i=w時,即Ww為交織車流交織強度系數;當i=nw時,即Wnw為非交織車流交織強度系數。

表2 計算交織強度系數時的常量

2)交織與非交織車速Vi

(2)

式中:VFF為基本路段的平均自由流速度,km/h。

當i=w時,即Vw為交織車輛區間平均速度,km/h;當i=nw時,即Vnw為非交織車輛區間平均速度,km/h。

3)交織區速度V

(3)

式中:Qnw為交織區非交織流量,pcu/h。

4)車流密度K

(4)

5)交織區長度Ls

(5)

城市快速路交織區路段內交織區總流量可以分為4種方向的OD需求,即Q=QFF+QFR+QRF+QRR,如圖3。

圖3 交織區內OD需求

主線到主線(freeway-to-freeway,FF),流量為QFF;主線到匝道(freeway-to-ramp,FR),流量為QFR;匝道到主線(ramp -to- freeway, RF),流量為QRF;匝道到匝道(ramp-to-ramp,FR),流量為QRR。通過不斷調整各種流向的流量即可得到應用于不同類型城市快速路交織區長度的計算模型。如輸入交織區總流量時QRR=0,而其他流向的交織區流量不變,可得到只進不出的城市快速路互通交織區長度計算模型;輸入交織區總流量時QRF=0,其他流向的交織區流量不變,可得到只出不進的城市快速路互通交織區長度計算模型。

2 基于可靠度理論的交織區分析

2.1 建立可靠度功能函數

交織區長度的作用,在于讓交織車輛的駕駛員在有限的時間和空間內實現行駛路徑變更,到達自己的期望車道[9]。交織區長度可靠性分析在應用可靠性理論知識時可闡述為:當交織車輛的駕駛人在交織區進行行駛,車輛需要在有限的交織區長度內實現行駛路徑變更,為使得駕駛員能夠按照自己的期望車速進行車道變換,需要有合適的交織區長度,這個交織區長度就是駕駛人駕駛汽車行駛在道路上為保證行車安全所需的交織區長度,可視為可靠性理論中的需求(與結構中的荷載效應相類似);而由道路為駕駛人所提供的交織區長度,在筆者研究中取規范中的下限(與結構中的抗力相類似)。因此,根據可靠度相關理論,可用式(6)描述交織區長度的可靠度功能函數C:

C=f(L)=LR-LS

(6)

式中:LR為交織區長度在《規范》中的范圍下限值;LS為保證行車安全所需的交織區長度。

在可靠度理論中通常采用可靠概率Ps、失效概率Pf、可靠指標β來進行衡量。β與Ps、Pf這3項指標具有一一對應的關系,即可靠指標β越大,可靠概率Ps越大,失效概率Pf反而越小。

2.2 可靠度功能函數參數分析

可靠度功能函數中涉及的變量較多,現將交織車輛區間平均速度、交織區基本路段的平均自由流速度作為隨機變量。

a、b、c、d與交織類型有關,確定其類型后,可將之作為確定性變量;在分析確定交織區中車道數的最不利情況是在約束運行的條件下,主線為單向雙車道,輔助車道為單車道的形式,且根據實地調查數據,三車道A型交織段的最大交織流量比為0.45,即Qr=0.45、N=3;Q交織區總流量則是根據所對應道路服務水平等級求得最大交織流量。因此,以上這些變量均可視為確定性變量。

目前,大多數研究認為在城市快速路交織區內,交織車輛區間平均速度、交織區基本路段的平均自由流速度基本服從正態分布。經過對武漢市快速路交織區進行實地調研,利用雷達微波監測數據。監測參數包括以車道為基礎的流量、速度等。在進行交織區選擇時,應選擇與研究對象相一致的帶有輔助車道的典型A型交織區,以及能夠較好的監測出交織區及與其相連的入匝道、出匝道交通流數據的地點。將采集到的城市快速路交織車輛區間平均速度和交織區基本路段的平均自由流速度作為統計樣本,經SPSS軟件K-S檢驗得到以下正態參數,如表3。

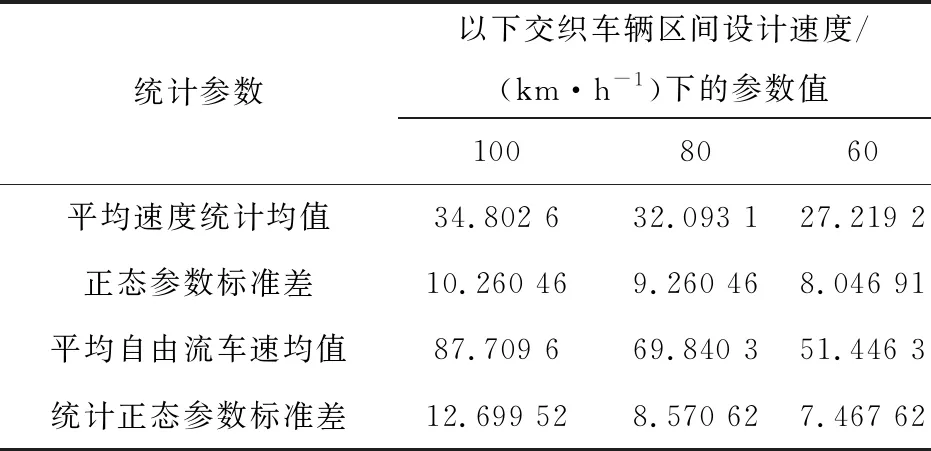
表3 運行速度統計正態參數

2.3 交織區長度可靠度

通過對以上各變量的研究與分析,采用式(6)建立交織區長度可靠度功能函數,檢驗我國現有規范中最小交織區長度的可靠性。目前,用可靠度理論知識結合城市快速路相關的設計研究較少,《規范》中沒有對在城市快速路中的可靠度應用做出明確規定,一般來講,由于交織區長度不足引發交通沖突頻發程度,及車輛行駛的安全情況受到威脅程度與由路面結構引發的事故程度相近,因此可以借鑒JTG 2120—2020《公路工程結構可靠性設計統一標準》[10]中對路面結構目標可靠度的規定,應用于筆者模型進行求解,如表4。

表4 不同城市道路等級的目標可靠性

現在以主線設計速度為100 km/h時,對最小交織區長度可靠度進行分析為例展開計算。

在Qr=0.45時,假設該城市快速路交織區每車道車流密度K=32.0 pcu/km,根據道路服務水平和最大交通流量一一對應的關系,可知該交織區的最大交織流量為4 480 pcu/h。交織區長度可靠性功能函數中采用的參數變量見表3。

采用交織區長度可靠度功能函數C,通過蒙特卡羅法計算其最小交織區長度的失效概率,式中LR=150 m,LS為的最小交織區長度計算如式(5),利用MATLAB進行計算,見表5。

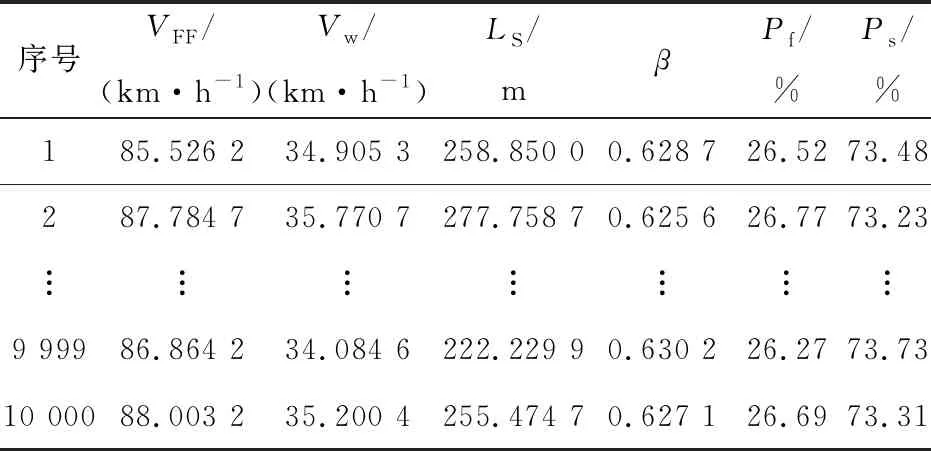
表5 LR=150 m時交織區長度對應可靠度計算

在主線設計速度為100 km/h的條件下,通過分析及表3可知,若交織區長度采用的是現行規范的最小值即LR=150 m時,其可靠度指標β≈0.625 6;失效概率Pf≈26.65%;可靠概率Ps≈73.35%,因此《規范》中最小交織區長度可靠性在一定程度上沒有符合安全等級為一級的可靠度要求(表4)。

同理,按照上述得分析步驟,亦可利用最小交織區長度可靠度功能函數計算出設計速度為80、60 km/h時現行規范中最小交織區長度的可靠度,結果如表6。

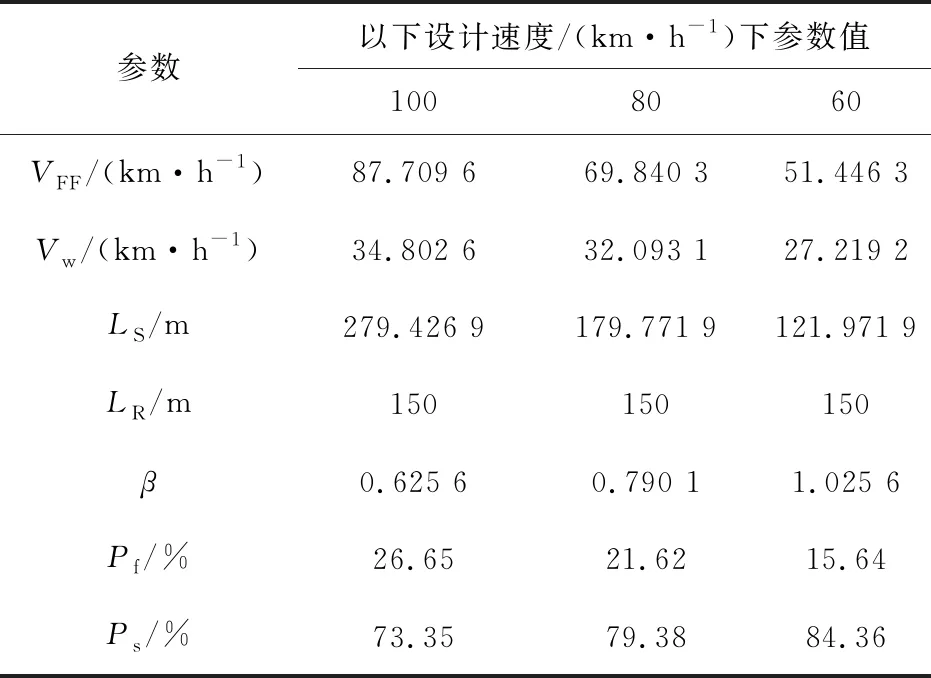
表6 可靠度功能函數計算結果

通過對表6數據的分析,在設計速度為100、80、60 km/h時,當采取現行規范中交織區長度的最小值LR=150 m時的失效概率Pf分別為26.65%、21.62%、15.64%,可靠概率Ps分別為73.35%、79.38%、84.36%,參考表4可知,采用該值作為最小交織區長度的安全可靠性在一定程度上沒有滿足安全等級為一級的安全可靠要求。因此,經筆者構建的交織區長度可靠度功能函數的檢驗,得出現行規范中所規定的交織區長度范圍的最小值可靠概率較低,即安全可靠性較低。

3 基于可靠度的交織區長度

現行規范中規定新建城市快速路的設計應采用三級服務水平,可根據滿足三級服務水平條件下,求出不同設計速度下交織區內總交通流量。由表4可知,城市快速路相對應的安全等級為一級,經過對已知相關參數變量的分析,反算筆者構建的交織區長度可靠度功能函數,從而得出所對應指標下道路所提供的交織區長度LR,所得對應數據見表7。

表7中的計算是在可靠概率95%的條件下進行反算,結果表明:當設計速度為100、80、60 km/h時,交織區長度的推薦值為400、370、350 m。

表7 交織區長度計算值及推薦選用值

4 實例分析

以某立交下游(由西向東方向)A型交織區為例,進行交織區長度可靠性分析,使用雷達槍,攝像機等儀器,通過錄像并輔以人工調查獲取交通流基礎數據,其中主線車道數為雙向四車道,設計速度為80 km/h;匝道車道數為單向一車道,設計速度為40 km/h,數據整理如表8。

表8 交織區交通流的基礎數據

4.1 計算過程

基于實地所收集到的交通流數據,利用交織區長度對應的可靠度功能函數,進行MATLAB計算,從而得到其交織區長度的失效概率,并得到滿足目標可靠度指標為1.64(即可靠概率為95%)所需的交織區長度。采用車流密度作為評價指標,將實例中所采用的交織區長度、滿足目標可靠度指標為1.64所需的交織區長度以及表7中相對應的推薦交織區長度進行對比分析。計算結果見表9。

4.2 結果分析

1)經過對表9的結果進行分析可知,交織區長度為160 m時容易造成路段的擁堵,這與該路段高峰時期經常發生擁堵現象嚴重的事實相吻合。若采用交織區長度363.12 m,在一定程度上可以緩解交通擁堵嚴重這個問題。

2)通過對表9中95%交織區長度以及表7中交織區推薦值的對比,發現在安全等級為一級時,即可靠概率95%的條件下進行反算出的交織區長度,可以看出其較好地符合表7中基于可靠度理論的交織區長度推薦選用值。

5 結 語

根據我國《公路通行能力手冊》中對交織區的相關理論知識,構建了城市快速路互通立交交織區長度計算模型,以該模型為基礎并引入可靠度理論知識建立最小交織區長度可靠度功能函數,檢驗現行規范中交織區長度最小值的可靠性,發現其可靠概率較低不滿足安全等級為一級的可靠性要求。根據在可靠概率95%的條件下即滿足一級安全等級的前提下進行反算,求解得出不同設計速度下相應地基于可靠度理論知識的交織區長度推薦選用值。鑒于目前對城市快速路互通立交交織區長度沒有明確的計算方法,在對以輔助車道相連的交織區長度設計時,為保證車輛完成車道變更行為所需要的距離且與城市快速路整體的道路通行能力相適應的要求,研究結論作為交織區長度設計取值的參考。