對流擴散方程最優控制問題的重心插值配點格式
黃蓉, 姚夢麗, 翁智峰
(華僑大學 數學科學學院, 福建 泉州 362021)
對流擴散方程描述的最優控制問題被廣泛應用于許多領域,如水污染處理[1]、空氣污染[2]等.對流擴散方程模擬一個化學或生物過程,涉及的物種相互之間會發生擴散、對流,因此,尋找穩定、高效的數值求解方法具有十分重要的實際意義.目前,許多學者已經提出許多數值求解格式,如間斷伽遼金方法[3]、雜交間斷伽遼金方法[4]、有限元方法[5-8]、雙線性偽譜方法[9]、勒讓德-伽遼金譜方法[10-11]、自適應間斷伽遼金方法[12]、譜伽遼金近似方法等[13-15].本文主要研究由對流擴散方程控制的最優控制問題.
1 預備知識
設區域Ω∈Rn(n=1,2)是帶有利普希茨邊界?Ω的空間有界域.考慮以下無約束最優控制問題,即
(1)
重心插值配點格式廣泛應用于數值求解各類微分方程,如平面彈性問題[16]、Volterra積分方程[17]、Allen-Cahn方程[18-19]、Burgers方程[20].重心插值配點格式是一種新型的無網格方法,能以機器精度任意逼近光滑函數,具有操作簡單、計算有效、精度高等優勢.然而,對重心插值配點格式求解微分方程的研究相對較少.Yi等[21]采用重點插值配點格式求解時間分數階電報方程,并給出理論分析.文獻[22-23]采用重心有理插值配點格式分別求解熱傳導方程、電報方程,并給出格式的誤差分析.Darehmiraki 等[24]基于重心插值配點格式,求解橢圓對流擴散方程的最優控制問題,并證明了配點格式的收斂性.
2 重心插值配點格式
2.1 重心Lagrange插值配點格式
假設存在n+1個互異節點xj,函數f(x)在節點xj處的函數值為fj(j=0,1,…,n).令插值多項式p(x)在節點處成立,p(xj)=fj,根據多項式的唯一性,p(x)可改寫為Lagrange插值形式,即
(2)
式(2)中:Lj(x)是Lagrange插值的基函數,滿足基函數的性質,有
(3)
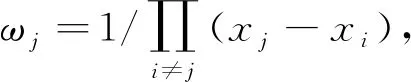
(4)
將式(4)代入式(2),可得
(5)
當p(x)=1時,有
(6)
結合式(5),(6),則重心Lagrange插值公式為
(7)
2.2 重心有理插值配點格式
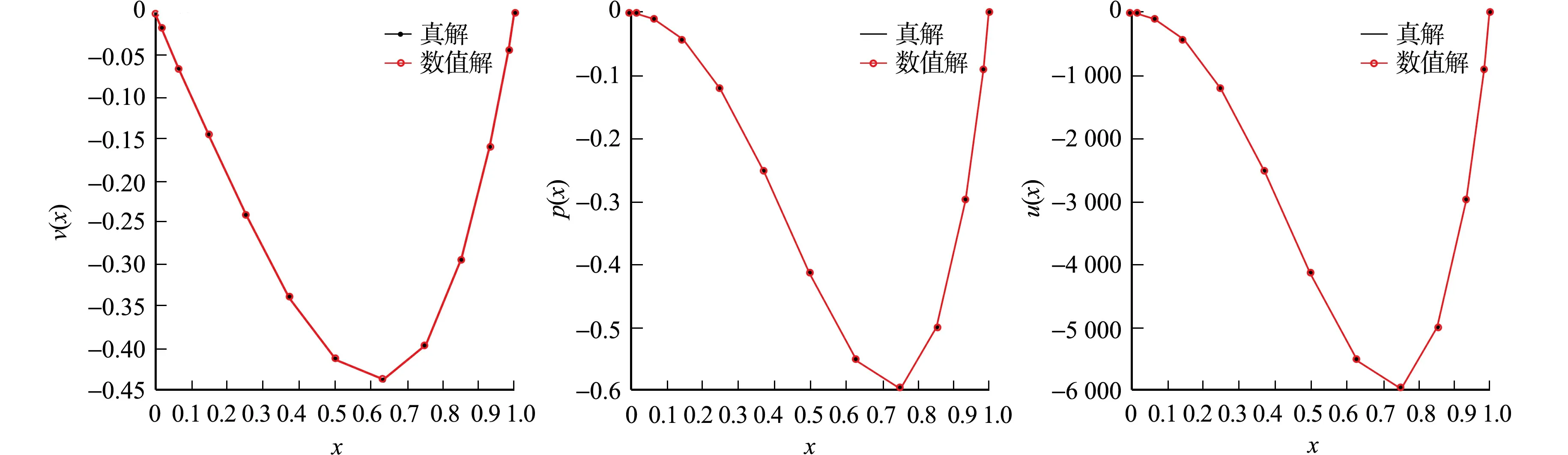
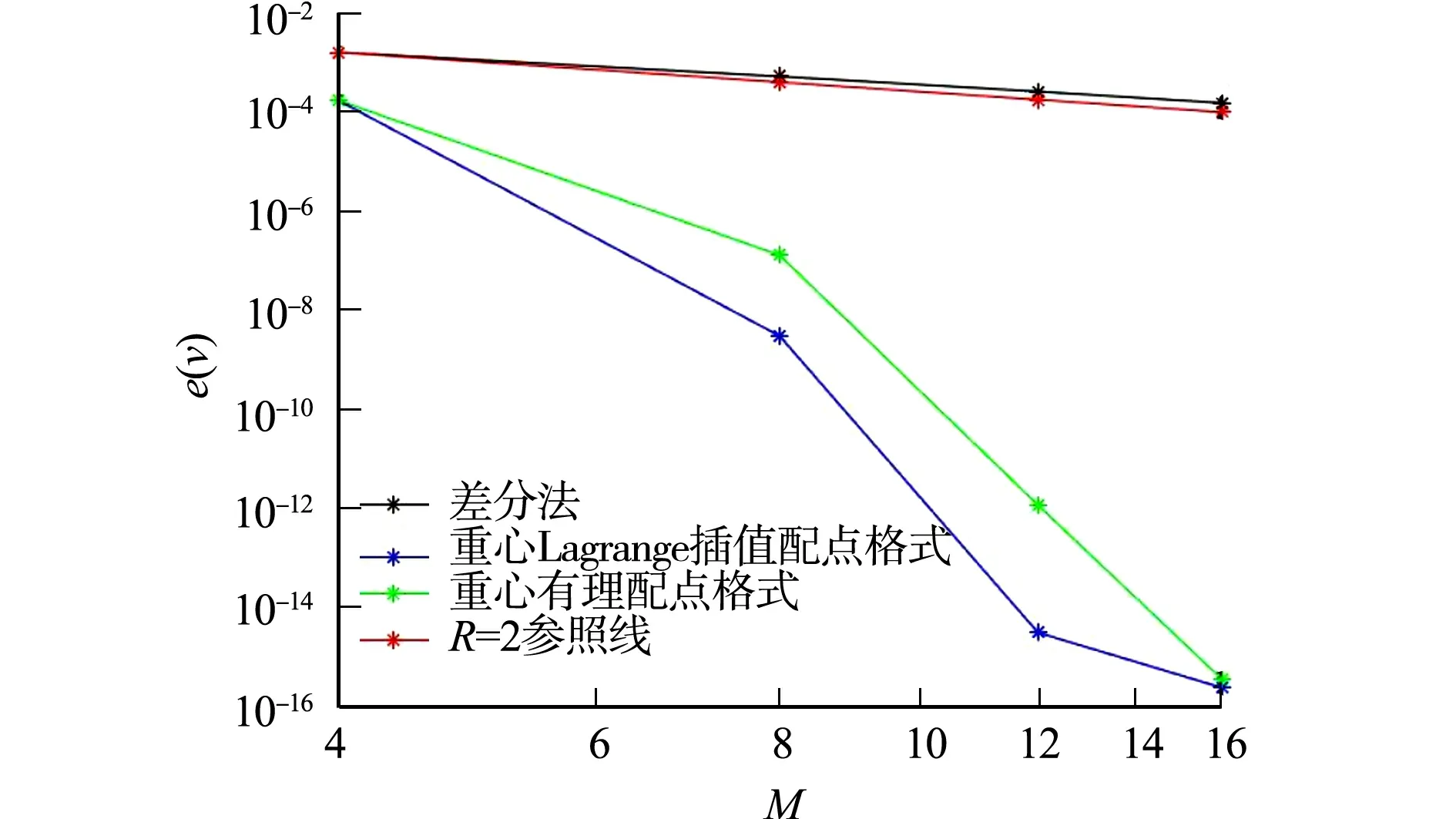
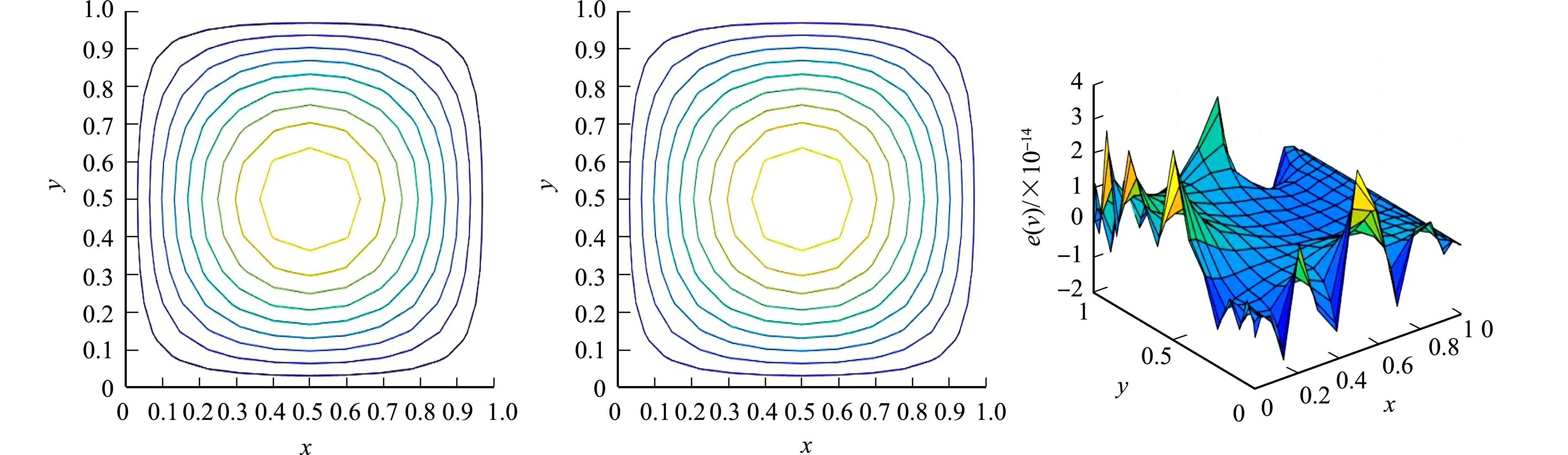
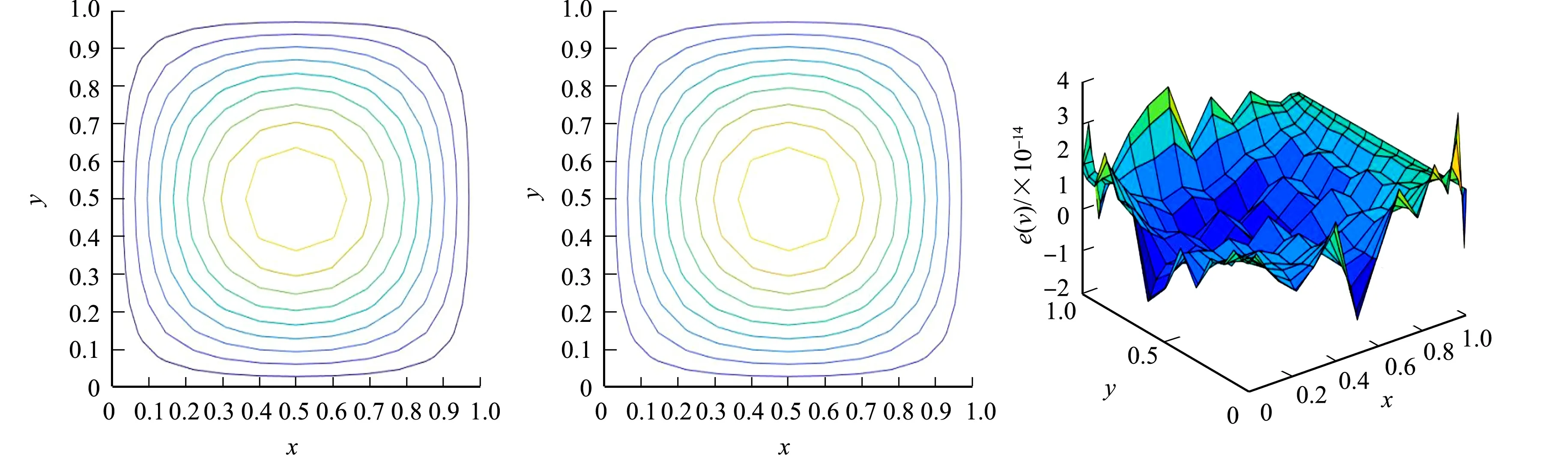
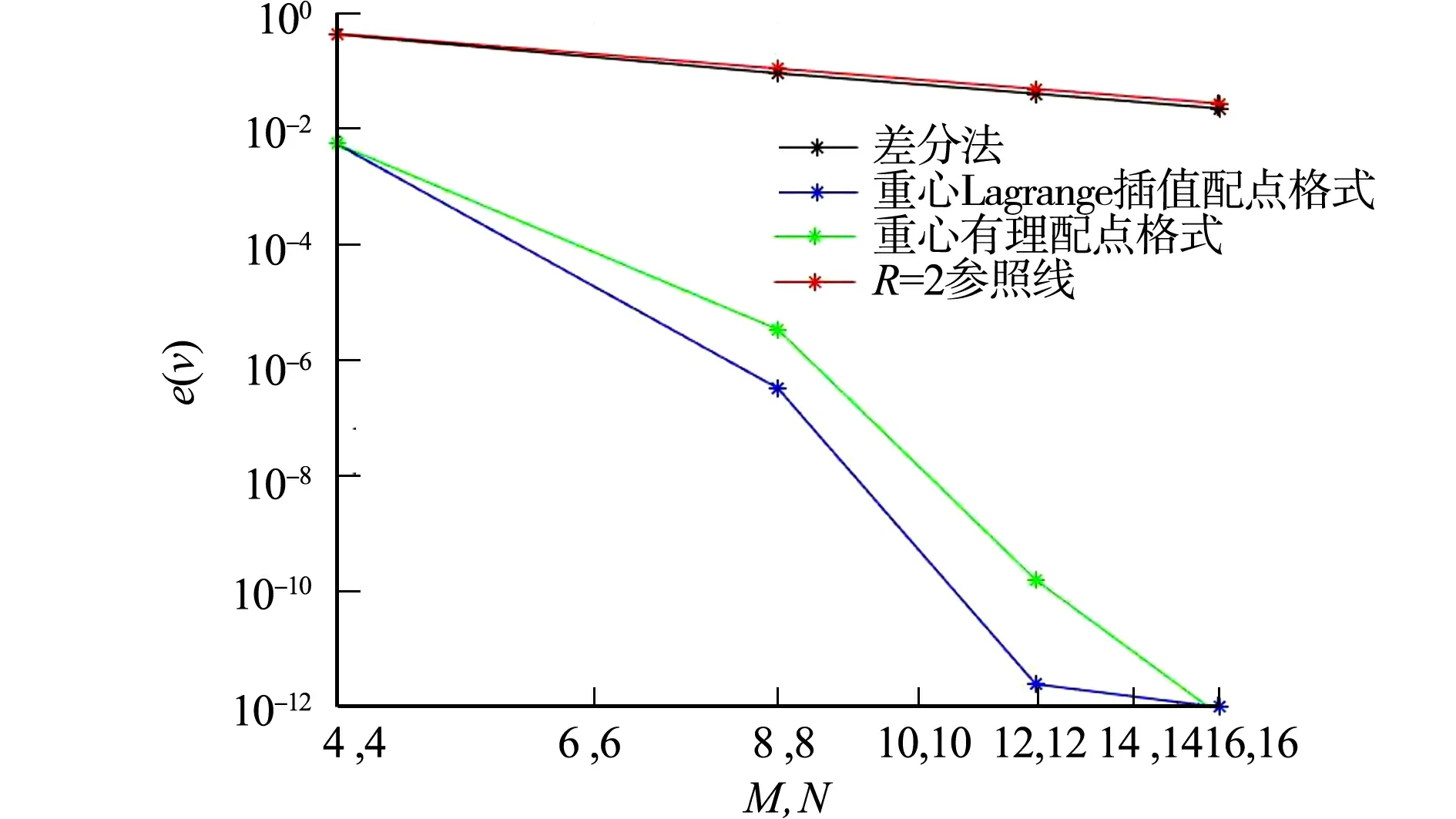
根據一維重心插值配點格式的推導過程,對于定義在區間[a,b]上的函數f(x),給定n+1個插值節點a=x0 (8) 將zk(x)改寫為Lagrange插值公式,即 (9) (10) 結合式(8)~(10),重心有理插值公式為 (11) 設p(x)為函數f(x)的重心Lagrange插值公式,則p(x)關于x求導,可得 (12) 針對對流擴散方程最優控制問題,采用Lagrange乘子求導數法,推出最優控制問題的最優性條件.對于最優控制問題(1),定義p為區域Ω上的Lagrange乘子,即 (13) 對式(13)進行泛函變分,對p求Frechet導數,推導得出狀態方程,即 (14) 對v求Frechet導數,導出伴隨方程為 (15) 類似地,對u求Frechet導數,則最優性方程為 γu-p=0. (16) 將對流擴散最優控制問題轉化為代數方程組,即 (17) 采用重心插值配點格式離散方程組,求解對流擴散方程最優控制問題的最優化條件,選取區域Ω=[0,1]×[0,1],α=(α1,α2)T,則化簡后的最優控制系統為 (18) 令空間x,y方向的節點分別是M,N,設v(x,y),p(x,y)的重心插值為 (19) 式(19)中:ψi(x),φj(y)分別是空間x,y方向上的基函數;vi,j=v(xi,yj);pi,j=p(xi,yj). 考慮v(x,y)對空間方向變量x,y求k+t階偏導數,即 (20) 偏導數在節點(xp,yr)處的函數近似值為 (21) 類似地,p(x,y)對空間方向變量x,y求k+t階偏導數,則偏導數在節點(xp,yr)處的近似值為 (22) 將式(21),(22)代入式(18)中,則對流擴散最優控制系統的重心插值配點格式離散格式為 (23) 式(23)的微分矩陣形式為 (24) 設函數u(x,y)運用重心Lagrange插值法逼近的數值解為pK,S(x,y),誤差函數e(x,y)為 e(x,y)=u(x,y)-pK,S(x,y). (25) 重心Lagrange插值公式的逼近性質,如引理1所示. 引理1[21]若u(x,y)∈C(n+1)(Ω),Ω是非空、具有Lipschitz連續邊界的開區域,則 (26) 類似地,有 (27) 根據引理1,可得定理1. 定理1設對流擴散方程最優控制問題中的狀態變量函數、伴隨變量函數分別是v(x,y),p(x,y),且v(x,y),p(x,y)∈C(n+1)(Ω),Ω=[a,b]×[c,d], 數值解分別是v(xk,ys),p(xk,ys),則 (28) 證明:定義線性微分算子D1,D2為 (29) 式(29)對應的離散格式為 (30) 為簡化分析過程,僅先分析與狀態量函數v(x,y)相關的項,將式(29),(30)相減,可得 D1v(x,y)-D1(xk,ys)=-ε[v(x,y)-vx,x(xk,ys)]-ε[v(x,y)-vy,y(xk,ys)]+ α1[v(x,y)-vx(xk,ys)]+α2[v(x,y)-vy(xk,ys)]- [v(x,y)-v(xk,ys)]=R1+R2+R3+R4+R5. (31) 式(31)中:R1=-ε[v(x,y)-vx,x(xk,ys)];R2=-ε[v(x,y)-vyy(xk,ys)];R3=α1[v(x,y)-vx(xk,ys)];R4=α2[v(x,y)-vy(xk,ys)];R5=-[v(x,y)-v(xk,ys)]. 根據引理1,有 (32) 類似地,可得 (33) (34) 同理,可推得 (35) 文獻[22]的定理的推導過程類似定理1,采用重心有理配點格式求解二維最優控制問題的相容性誤差,即定理2. 定理2設v(x,y),p(x,y)分別是對流擴散控制問題中的狀態量函數、伴隨量函數,v(x,y),p(x,y)∈C(n+1)(Ω),Ω=[a,b]×[c,d],v(xk,ys),p(xk,ys)分別是v(x,y),p(x,y)運用重心有理配點格式求解的數值解,則 (36) 式(36)中:C=c·max{ε,α1,α2,(1/γ)},c為常數;h1,h2分別是空間x,y方向的步長. 為便于分析,定義最大相對誤差為 (37) 一維、二維的最優控制問題分別采用切比雪夫重心插值配點格式、有限差分法兩種離散方法,比較算例的數值結果,驗證配點格式的有效性及高精度.對于一維最優控制問題,選取的真解為 v(x)=x(x-1)ex,p(x)=2x2(x-1)ex. (38) 選取區域Ω=[0,1],ε=10-6,α=10-3,γ=10-4,令節點數為M=12,重心Lagrange插值配點格式、重心有理插值配點格式的數值解圖,分別如圖1,2所示. (a) v(x) (b) p(x) (c) u(x) (a) v(x) (b) p(x) (c) u(x) 由圖1,2可知:對于狀態量、伴隨量、控制量,采用兩種重心插值配點格式求解的數值解圖均逼近解析解圖,表明該數值算法是穩定的. 分別選取ε,α,γ的不同剖分,重心Lagrange插值配點格式、重心有理配點格式、差分法的最大相對誤差(e),如表1,2,3所示.狀態量的收斂階(R)對比,如圖3所示. 表1 重心Lagrange插值配點格式的最大相對誤差(M) 表2 重心有理配點格式的最大相對誤差(M) 表3 差分法求解的最大相對誤差(M) 圖3 狀態量的收斂階對比(m) 由表1~3可知:采用重心插值配點格式求解變量比差分法求解時的誤差更小,剖分少量節點,可達到格式高精度.當選取的節點數相同時,采用重心Lagrange插值比重心有理插值求解方程的誤差更小.由圖3可知:差分法格式的收斂階是二階,配點格式滿足指數收斂性質. v(x,y)=sin(πx)sin(πy),p(x,y)=π2sin(πx)sin(πy). (39) (40) 選取區域Ω=[0,1]×[0,1],α=(1,1)T,γ=0.5,ε=0.1,令節點數為M=16,N=16,則重心Lagrange插值配點格式、重心整理插值配點格式的精確解、數值解與誤差,分別如圖4,5所示.由圖4,5可知:采用兩種重心插值配點格式求解狀態量、伴隨量的精確解圖像與數值解圖像逼近,且最大相對誤差精度高,可達到10-13量級,表明兩種重心插值配點格式均穩定. (a) 狀態量的精確解 (b) 狀態量的數值解 (c) 狀態量的誤差 分別選取不同的剖分節點數,重心Lagrange插值配點格式、重心有理配點格式、差分法的最大相對誤差,如表4,5,6所示.由表4,5可知:最大相對誤差可達到10-11量級,表明兩種重心插值配點格式均具有高精度,且前者的求解效果略優于后者.隨著剖分變細,3種變量的最大相對誤差在逐漸減少.由表6可知:選取M=64,N=64,狀態量、伴隨量、控制量的最大相對誤差分別達到10-3,10-4,10-4量級;與經典的差分法比較,重心插值配點格式選取更少的節點,即可達到更高的精度. 表4 重心Lagrange插值配點格式最大相對誤差(M,N) 表5 重心有理配點格式的最大相對誤差(M,N) 表6 差分法求解的最大相對誤差(M,N) (a) 狀態量的精確解 (b) 狀態量的數值解 (c) 狀態量的誤差 狀態量收斂階對比,如圖6所示.由圖6可知:采用差分法求解方程的收斂階為2階;重心Lagrange插值配點格式、重心有理配點格式的收斂階都呈現指數遞減的效果,前者的收斂效果優于后者. 圖6 狀態量收斂階對比(m,n) 基于Lagrange乘子法,將對流擴散最優控制問題轉化為由狀態方程、伴隨方程、最優性方程三者聯立形成的代數方程組,再分別采用重心Lagrange插值配點格式、重心有理插值配點格式離散求解方程組中的狀態量v、伴隨量p,并對提出的配點格式進行相容性誤差分析.數值實驗結果表明,兩種重心插值配點格式均具有高精度的特性,選取切比雪夫節點時具有指數收斂的效果.此外,與經典的有限差分格式相比,該配點格式在剖分較少的節點數時,可達到很高的精度.2.3 重心插值配點格式的微分矩陣
3 對流擴散方程最優控制問題的離散格式
3.1 最優性條件


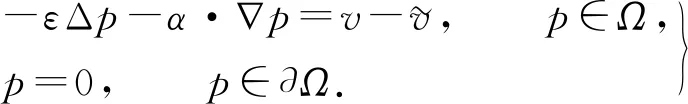
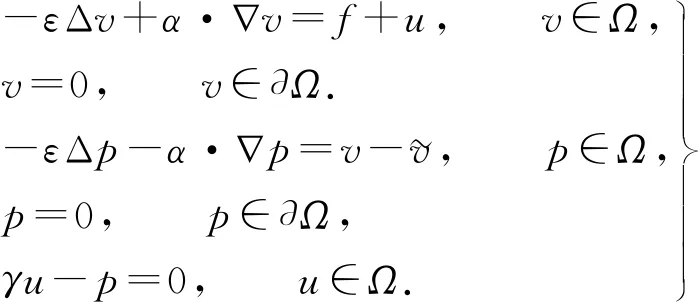
3.2 對流擴散方程最優控制問題的離散格式
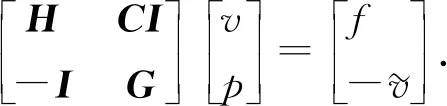
3.3 相容性分析

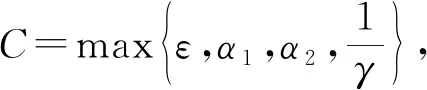
4 數值算例
4.1 算例1




4.2 算例2
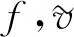



5 結束語

