紙木蜂窩板面外靜態壓縮有限元仿真分析

曹敏娜，楊國超，張求慧

紙木蜂窩板面外靜態壓縮有限元仿真分析

曹敏娜a，楊國超b，張求慧b

（北京林業大學 a.木質材料科學與應用教育部重點實驗室 b.木材科學與工程北京重點實驗室，北京 100083）

探究紙木蜂窩板的壓潰模式和單個蜂窩單元的變形失效模式，為紙木蜂窩板內部失效機制提供一定的理論基礎。通過有限元仿真模擬，分析面外靜態壓縮得到變形云圖、應力–應變云圖和應力–應變曲線。紙木蜂窩板的受壓過程分為4個階段，應力集中分布在蜂窩芯層，最外側的蜂窩最早出現變形且變形較大，隨后中間區域的蜂窩逐步變形增大。蜂窩芯層在受壓時存在至多1個應力峰，蜂窩壁彎曲折疊了1～2次，產生了1～2個塑性鉸，并在此過程中吸收能量。紙木蜂窩板的壓潰失效趨勢為由外側蜂窩向內部蜂窩，由單層壁向雙層壁，由最弱的壓潰點向其余位置。

紙木蜂窩板；蜂窩芯層；面外靜態壓縮；有限元

蜂窩夾層板是一種環境友好的仿生材料，多孔的蜂窩結構使其具備比強度高、質量小、抗沖擊性高、緩沖隔振好等優點，目前已廣泛應用在緩沖包裝、運輸和家具領域[1-3]。在運輸傳遞過程中，蜂窩板會受到靜載荷、沖擊振動等作用力，有限元仿真技術已經應用到蜂窩板平面承載性能和緩沖振動的模擬分析中[4-6]。

目前，國內外學者對蜂窩板的研究集中在蜂窩芯層和面板為同質材料的分析，尤其集中在對蜂窩紙板和金屬蜂窩板的力學性能研究和有限元分析，對關于采用2種材料的復合蜂窩板的研究較為少見[7-8]。將紙蜂窩和木板2種基材制備成紙木蜂窩板，其力學性能和抗彎性能要優于傳統蜂窩紙板的，強重比又高于普通板材的。已有學者對紙木蜂窩板進行了力學性能研究，但有關有限元仿真的分析還未見報道。在紙木蜂窩板的各項力學性能中，面外靜態壓縮機理復雜，涉及到蜂窩芯層的局部失穩。由于測試手段的限制，試驗只能觀察到最外側的部分蜂窩壁的變形失效，無法測得蜂窩芯層內部的應力、應變變化和單個蜂窩單元的失效模式。基于此，本文以正六邊形紙蜂窩作為芯層，以三層楊木膠合板作為結構面板，提出一種紙木復合的蜂窩板結構。應用試驗和有限元分析相結合的方式分析紙木蜂窩板的面外靜態壓縮過程，探究紙木蜂窩板的壓潰模式和蜂窩單元的變形失效模式，為紙木蜂窩板的平面力學性能和后續應用提供理論基礎。

1 紙木蜂窩板仿真模型及材料參數

1.1 幾何結構

紙木蜂窩板的正六邊形蜂窩芯層由瓦楞紙沿縱向施膠黏接后拉伸制成，故蜂窩單元在厚度上會分為單層壁厚和雙層壁厚。規定蜂窩芯層拉伸成型前的長度方向為縱方向，簡稱，對應空間坐標方向；蜂窩芯層的拉伸方向為橫方向，簡稱，對應空間坐標方向；蜂窩芯層的厚度方向為，對應空間坐標方向，如圖1所示。除最外層蜂窩單元外壁外，所有垂直于方向的蜂窩單元壁均為雙層壁厚。在Solidworks中對紙蜂窩芯層和膠合板面板分別建模，采用自下而上的方式進行裝配體組合，導入Ansys Workbench進行有限元仿真分析。由于瓦楞紙芯紙在厚度方向上的尺寸遠遠小于其他2個方向，在壓縮過程中會產生失穩導致大變形。為確保仿真精度，蜂窩芯層采用殼單元Shell181建模更為合理，膠合板面板采用實體單元Solid186建模。根據GB/T 1453—2022《夾層結構或芯子平壓性能試驗方法》[9]中的規定，蜂窩芯層尺寸為60 mm×60 mm，厚度為15 mm。在切割制樣過程中為保證紙蜂窩尺寸符合國家標準，蜂窩芯層在2個側面會產生非封閉的蜂窩單元，在受力后會更容易出現局部應力集中現象[10]。為更好地等效紙木蜂窩板受力情況，將兩側未封閉的蜂窩單元進行還原建模，即紙木蜂窩板的4個側面形狀各不相同。將紙蜂窩芯層全封閉的2個側面記作Ⅰ，未封閉的2個側面記作Ⅱ，紙木蜂窩板的模型如圖2所示。

1.2 材料參數

紙木蜂窩板的面外靜態壓縮過程涉及材料非線性、幾何非線性和狀態非線性，是一個復雜的非線性響應過程，還存在壓縮后的大變形和接觸問題[11]。采用雙線性正交各向異性彈塑性材料模型定義瓦楞原紙和膠合板的材料本構關系。紙蜂窩芯層由定量為95.2 g/m2的高強瓦楞紙制備，瓦楞原紙的厚度根據GB/T 451.3—2002《紙和紙板的厚度測定》[12]進行測定。由于瓦楞紙原紙的材料特性，壓縮試驗難度極大，根據GB/T 12914—2018《紙和紙板抗張強度的測定恒速拉伸法（20 mm/min）》[13]，通過萬能力學試驗機對瓦楞紙進行拉伸試驗，獲得其力學參數。參考Mann等[14]、Baum等[15]和Persson等[16]的研究成果，根據經驗公式（1）獲得其他參數。面外靜態壓縮方向為瓦楞紙的縱向，對應材料參數中的方向，試驗過程中瓦楞紙在此方向發生屈曲變形。瓦楞紙屬于屈服現象不明顯的材料，規定屈服強度為材料產生0.2%的應變時的應力值，測得試驗數值為2.28 MPa。瓦楞紙在厚度方向上的尺寸遠遠小于其他2個方向的。泊松比μ取0.3，μ和μ在計算中通常取0.01。按照GB/T 17657—2013《人造板及飾面人造板理化性能試驗方法》[17]對膠合板的密度進行測定，通過萬能力學試驗機進行抗壓力學試驗。根據GB/T 1453—2022《夾層結構或芯子平壓性能試驗方法》[9]對紙木蜂窩板進行面外靜態壓縮試驗。最后獲得的材料參數如表1所示。

圖1 紙蜂窩芯層結構

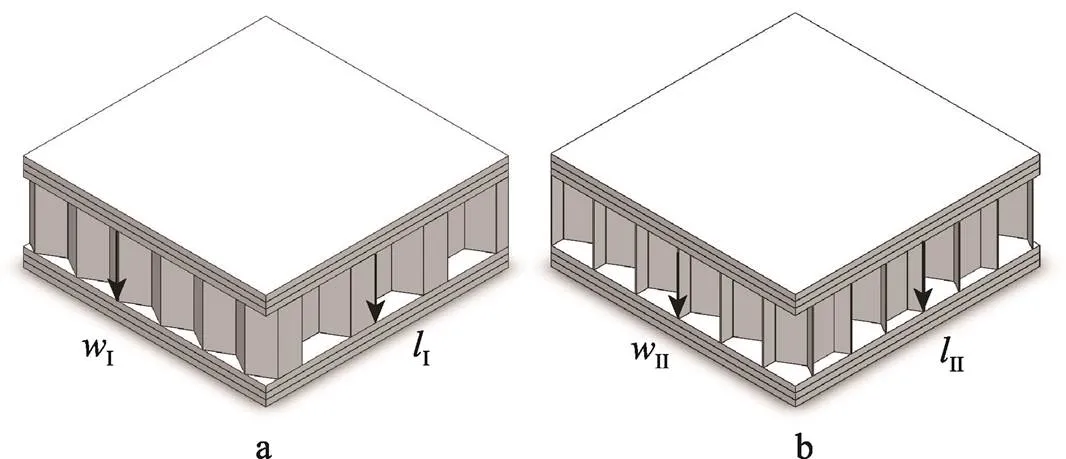
圖2 紙木蜂窩板模型

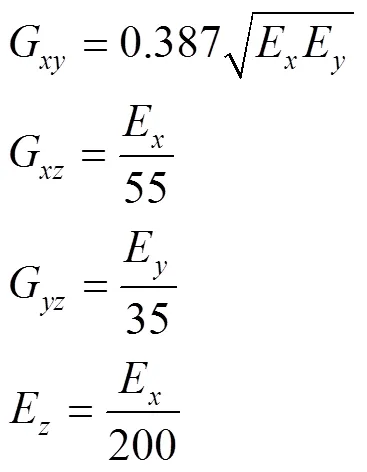
表1 材料參數

Tab.1 Material parameters

1.3 分析設定

將紙木蜂窩板上下面板和蜂窩芯層分別建立部件，部件表示具有相同單元類型的單元集合，可實現共享網格、節點耦合，每個部件可以單獨配置材料屬性，自成一體。紙木蜂窩板的上下面板和蜂窩芯層是黏接而成的，在試驗過程中未發生脫膠現象，在有限元分析的接觸定義中選擇綁定約束，以便在仿真模擬過程中實現整體效應，不發生分離。部件內部已默認接觸無須再重復設置，只需對部件間設置綁定接觸，即將蜂窩芯層上表面的所有邊與上面板的下表面進行綁定，將蜂窩芯層下表面的所有邊與下面板的上表面進行綁定。網格劃分精度對仿真模擬結果會產生較大影響，高質量的網格有更好的邊界網格形態，能夠獲取更精確的解。對膠合板面板采用Hex六面體網格劃分，對紙蜂窩芯層采用Qaud四邊形網格劃分。劃分后單元質量高達0.999 6，共計82 903個節點、20 460個單元。

對紙木蜂窩板施加方向的位移載荷，在求解結果中分別提取支反力與方向定向變形值隨時間變化的曲線，轉化整合成仿真的應力–應變曲線。為了更好地對比試驗與仿真結果，本文挑選一組試驗的應力–應變曲線與仿真曲線進行對比，結果見圖3。試驗獲得的平壓強度均值為0.153 MPa，有限元模擬值為0.143 MPa，數值非常接近，如表2所示。仿真曲線相比試驗曲線更平滑，尤其是在平臺階段，這主要是由于實際試驗時蜂窩芯層在坍塌堆疊后可能會與周邊蜂窩接觸，蜂窩間存在支撐作用，讓已經到達平臺階段的蜂窩，仍有可能產生應力的二次上升。總的來看，仿真結果與試驗結果呈現高度一致性，驗證了有限元仿真的準確性。

2 結果與分析

2.1 整體變形

紙木蜂窩板整體壓縮變形過程和應力云圖如圖4所示。從應力分布可以清晰看到，應力集中分布在蜂窩芯層，面板受到的應力遠遠小于紙蜂窩芯層的應力。變形失效破壞的位置發生在紙蜂窩芯層部位，面板的變形值很小，這也與試驗結果相符合。在一定范圍內，紙木蜂窩板的承載能力主要由芯層決定，面板的強度對蜂窩板性能影響不大[18]。

圖3 紙木蜂窩板試驗與仿真的應力–應變曲線

表2 紙木蜂窩板試驗與仿真的平壓強度

Tab.2 Test and simulation flatwise compression properties of paper-wood honeycomb board

紙木蜂窩板的靜態壓縮過程可以分成4個階段。第1階段是彈性階段，這個階段分為2個部分：在壓縮初期，蜂窩壁在軸向發生彈性變形，此時應力隨應變線性增加；若繼續加載超過彈性極限后，就變成非線性的彈性變形，直至達到蜂窩芯層的臨界最大屈曲載荷，試件發生破壞。第2階段是彈塑性屈曲階段，應力隨應變的增加而減少，此時由彈性變形導致的局部坍塌轉變為以塑性鉸為特征的屈曲；屈曲首先發生在單層壁上，隨后發生在雙層壁上。第3階段是塑性坍塌階段，應變持續增加，應力基本保持不變，呈現出近似平臺的區域，平臺的寬度代表了蜂窩板緩沖吸能的能力。此階段表現為以蜂窩壁塑性坍塌為主的持續壓潰過程，壓潰載荷隨應變的增加呈現一定的上下波動，直至完全被壓塌。第4階段是密實化階段，蜂窩壁充分坍塌變形發生接觸，直至蜂窩芯層完全被壓實，此時微小應變將引起應力急劇增大[19]。紙木蜂窩板的壓縮過程以蜂窩芯層單層壁的失穩為開始，以雙層壁達到最大承載力發生破壞為結束。

為更清楚地了解紙蜂窩芯層的壓潰過程，將上下面板進行隱藏，觀察蜂窩芯層在持續載荷作用下的應力云圖。如圖5所示，蜂窩芯層的變形不同步，呈現一定的先后順序。從總體來看，應力集中最早出現在最外側的蜂窩單層壁的中心區域，而后逐漸向中間區域的蜂窩單元擴展，外側相對自由的蜂窩單層壁應力較大。有限元模擬的變形過程與試驗圖相對應，可見試驗過程中蜂窩芯層最外側首先發生變形，尤其是4個角落的處的蜂窩變形明顯。這是由于最外側存在未封閉的單層壁蜂窩，其抗壓能力要弱于全封閉的蜂窩，也弱于雙層壁的蜂窩，因此首先出現應力集中和大變形。隨著位移載荷的增大，中間區域的單層壁蜂窩也發生較大的變形，主要載荷由中間區域的雙層壁蜂窩承擔，出現大應力，最終全部蜂窩都被屈服壓潰[20]。對應試驗圖同樣可以看到變形逐步由最外側向中心處的蜂窩移動，隨著位移載荷的持續增大，中間區域蜂窩變形值也逐步增加。對每個獨立的蜂窩單元而言，應力集中最早出現在蜂窩的上下節點連線的中心區域，隨著位移載荷的增加先沿著豎直方向由中心區域向上下節點擴展；然后在水平方向上由各節點和節點連線向周圍擴展，直至全部被壓潰變形。對于單個獨立的蜂窩的變形，實際試驗不能達到有限元模擬的理想狀態，其屈服并非一定發生在蜂窩上下節點連線的中心區域，也有可能在蜂窩芯層最上端或最下端首先發生屈服變形。試驗過程中屈服壓潰順序取決于對應區域壓潰點的強弱，最弱的壓潰點所在區域首先被壓潰。

2.2 單個蜂窩變形

為進一步探究受壓時處于不同位置的單個蜂窩單元在直立壁高度方向上的變形情況，分別在紙蜂窩芯層的中心蜂窩上取一條平行軸的路徑，4個側面Ⅰ、Ⅱ、Ⅰ、Ⅱ的蜂窩上同樣各取一條平行軸的同名路徑。路徑方向由節點1指向節點2，節點1代表起始位置0，分析5條異面路徑的等效應力和應變的分布情況。其中等效總應變是包括彈性應變和塑性應變在內的應變總和。

如圖6所示，單個蜂窩單元的受壓變形主要表現為在近似節點1和節點2的連線中心處對稱面發生彎曲、局部的變形折疊。根據Wierzbicki[21]的研究表明，蜂窩壁每彎曲折疊一次都會產生一個塑性鉸，按照波長進行漸進折疊，而波長約等于蜂窩單元邊長。因此蜂窩單元高度越大，邊長越小，產生的塑性鉸會越多，能量吸收就越多。本研究中紙蜂窩芯層的蜂窩單元邊長為6 mm，故在壓縮過程中將按照=6 mm進行漸進折疊，蜂窩單元高度為15 mm，蜂窩芯層將折疊1～2次，如圖6可見蜂窩壁產生了1～2個塑性鉸。外側的封閉蜂窩單元折疊彎曲對稱度更高，發生折疊的區域相對小而集中；外側的未封閉蜂窩單元彎曲扭曲度更高，發生折疊的區域更大，并呈現出一定的非對稱性，這可能與較弱的承載能力所導致的應力分布不均有關；處在中心區域的蜂窩單元雖承受較大應力，但整體變形較小，未見其在高度方向發生彎曲折疊。外側的蜂窩壁比中心處的蜂窩壁有更大的變形，首先發生彎曲失效，這也與試驗結果相匹配。

圖4 紙木蜂窩板靜態壓縮過程

圖5 紙蜂窩靜態壓縮過程

圖7為5條路徑由節點1至節點2的應力和應變曲線，處在封閉蜂窩單元的路徑Ⅰ和Ⅰ分別在靠近上下面板6 mm左右的位置，即在距離為6 mm和9 mm處產生了應力峰值，這與上文提及的塑性鉸產生的位置對應。應力峰處對應的位置代表可能壓潰的點，雖然在7.5 mm處，即1/2處的應力較小，但由于塑性鉸的存在，在此產生了最大變形和應變。未封閉的蜂窩單元Ⅱ和Ⅱ在靠近上下面板的位置和1/2處均產生了應力峰，這些均為可能的壓潰點。壓潰點并非同時被壓潰，往往是較弱的首先被壓潰，然后逐步向其他的壓潰點擴展[15]。由應變曲線可見，未封閉的蜂窩單元也在約1/2處壓潰點發生了大變形，可見1/2處的壓潰點相對較弱。處在中心處的蜂窩單元的壓潰點更多，應力–應變分布更為均勻。處在外側的封閉的蜂窩單元可承受的應力峰值最大，約為外側未封閉的蜂窩單元可承受應力的2倍，中心的蜂窩單元應力承受能力次之。

圖6 單個蜂窩的應力應變云圖

圖7 單個蜂窩的應力–應變曲線

3 結語

通過試驗測試和有限元仿真模擬，研究了紙木蜂窩板在面外靜態壓縮下的整體壓潰機制和單個蜂窩單元的變形失效模式。紙木蜂窩板的受壓過程分為4個階段，應力集中分布在蜂窩芯層，面板受到的應力很小，承載能力主要由蜂窩芯層決定。蜂窩芯層的變形最早出現在最外側的蜂窩，隨著位移載荷的增大中間區域的蜂窩變形逐步增大，直至全部蜂窩屈服壓潰。處在外側的蜂窩相比于中心的蜂窩會發生更大的變形，蜂窩在受壓時會按照波長約等于蜂窩單元邊長進行漸進折疊，每折疊一次產生一個塑性鉸，在此過程中吸收能量。壓縮過程中蜂窩壁存在1到多個應力峰，這些應力峰代表著可能的壓潰點，較弱的首先被壓潰，文中多為1/2處的壓潰點首先被壓潰，然后逐步向其他的壓潰點擴展。綜上，紙木蜂窩板的壓潰失效規律總的趨勢為由外側向內部，由單層壁向雙層壁，由最弱的壓潰點向其余位置。本文探究了蜂窩芯層內部的應力–應變和單個蜂窩的失效模式，為紙木蜂窩板的平壓性能探究和后續應用提供一定的理論和技術支持。

[1] OZEN I, AVA K, GEDIKLI H, et al. Low-energy Impact Response of Composite Sandwich Panels with Thermoplastic Honeycomb and Reen-Trant Cores[J]. Thin-Walled Structures, 2020, 156: 106-989.

[2] ZHANG Xiao-ming, XIE Juan, CHEN Jin-xiang, et al. The Beetle Elytron Plate: A Lightweight, High-Strength and Buffering Functional-Structural Bionic Material[J]. Scientific Reports, 2017, 7(1): 4440.

[3] 王強, 王寧, 王鈴偉, 等. 輕質蜂窩形仿生材料在家具設計中的應用與發展研究[J]. 家具與室內裝飾, 2020(10): 82-84.

WANG Qiang, WANG Ning, WANG Ling-wei, et al. Study on Application and Development of Lightweight Honeycomb Bionic Materials in Furniture Design[J]. Furniture & Interior Design, 2020(10): 82-84.

[4] 李娜, 尤青文. 蜂窩夾層復合材料小質量沖擊接觸力的分析[J]. 科學技術與工程, 2020, 20(14): 5558-5565.

LI Na, YOU Qing-wen. Analysis on Contact Force of Small-Mass-Impact on Honeycomb Sandwich Composites[J]. Science Technology and Engineering, 2020, 20(14): 5558-5565.

[5] 楊震, 李賜生. 實木家具包裝箱的設計與探討[J]. 家具與室內裝飾, 2018(12): 110-111.

YANG Zhen, LI Ci-sheng. Design and Discussion of Solid Wood Furniture Packaging Cases[J]. Furniture & Interior Design, 2018(12): 110-111.

[6] 楊穩, 張勝蘭, 李瑩. 蜂窩夾層結構等效模型研究進展[J]. 復合材料科學與工程, 2020(10): 122-128.

YANG Wen, ZHANG Sheng-lan, LI Ying. Research Progress of Equivalent Model of Honeycomb Sandwich Structure[J]. Composites Science and Engineering, 2020(10): 122-128.

[7] 王宏磊. 蜂窩夾芯復合材料的力學性能研究[D]. 吉林: 吉林大學, 2019: 1-3.

Wang Hong-lei. Mechanical Properties of Honeycomb Sandwich Composites[D]. Jilin: Jilin University, 2019: 1-3.

[8] 楊雨恒, 張周鎖, 史文博, 等. 鋁蜂窩夾層板動力學建模仿真與試驗驗證[J]. 機械設計, 2021, 38(8): 9-16.

YANG Yu-heng, ZHANG Zhou-suo, SHI Wen-bo, et al. Dynamic Modeling Simulation and Experimental Verification of the Aluminum Honeycomb Sandwich Panel[J]. Journal of Machine Design, 2021, 38(8): 9-16.

[9] GB/T 1453—2022, 夾層結構或芯子平壓性能試驗方法[S].

GB/T 1453—2022, Test Method for Flatwise Compression Properties of Sandwich Constructions or Cores[S].

[10] 潘鳳麗, 李光. 基于Ansys Workbench的塑料蜂窩板仿真分析及優化[J]. 包裝工程, 2016, 37(23): 44-49.

PAN Feng-li, LI Guang. Ansys Workbench-Based Simulation Analysis and Optimization of Plastic Perforated Board[J]. Packaging Engineering, 2016, 37(23): 44-49.

[11] 湯金若, 朱瑾, 于江祥. 曲面蜂窩板的彎曲特性仿真分析研究[J]. 現代防御技術, 2016, 44(5): 186-193.

TANG Jin-ruo, ZHU Jin, YU Jiang-xiang. Simulations on Buckling Characteristics of Curving Honeycomb[J]. Modern Defense Technology, 2016, 44(5): 186-193.

[12] GB/T 451.3—2002, 紙和紙板的厚度測定[S].

GB/T 451.3—2002, Paper and Board-Determination of Thickness[S].

[13] GB/T 12914—2018, 紙和紙板抗張強度的測定恒速拉伸法(20 mm/min)[S].

GB/T 12914—2008, Paper and Board-Determination of Tensile Properties-Constant Rate of Elongation Method(20 mm/min)[S].

[14] MANN R W, BAUM G A, HABEGER C C, et al. Determination of All Nine Orthotropic Elastic Constants for Machine-made Paper[J]. Appleton Wisconsin the Institute, 1980, 63(2): 163-166.

[15] BAUM G A, BRENNAN D C, HABEGER C C. Orthotropic Elastic-constants of Paper[J]. Tappi Journal, 1981, 64(8): 97-101.

[16] PERSSON K. Material Model for Paper: Experimental and Theoretical Aspects[D]. Lund: Lund University, 1991.

[17] GB/T 17657—2013, 人造板及飾面人造板理化性能試驗方法[S].

GB/T 17657—2013, Test Methods of Evaluating the Properties of Wood-based Panels and Surface Decorated Wood-based Panels[S].

[18] 李厚民. 蜂窩紙板受壓時的有限元分析[J]. 包裝工程, 2006, 27(1): 34-36.

LI Hou-min. FEM Analysis of the Compression Properties of Honeycomb Paperboard[J]. Packaging Engineering, 2006, 27(1): 34-36.

[19] 陳岳鈴, 王軍, 盧立新, 等. 凹六邊形蜂窩紙板面內承載性能有限元仿真分析[J]. 包裝工程, 2021, 42(13): 174-179.

CHEN Yue-ling, WANG Jun, LU Li-xin, et al. Finite Element Simulation Analysis of In-Plane Load-Bearing Performance of the Paperboard with re-Entrant Hexagonal Honeycomb Core[J]. Packaging Engineering, 2021, 42(13): 174-179.

[20] 李楊, 賁小軍, 袁建東, 等. 熱塑性蜂窩板的平壓性能分析[J]. 包裝學報, 2022, 14(2): 93-97.

LI Yang, BEN Xiao-jun, YUAN Jian-dong, et al. Analysis of Flat Compression Performance of Thermoplastic Honeycomb Panel[J]. Packaging Journal, 2022, 14(2): 93-97.

[21] WIERZBICKI T. Crushing Analysis of Metal Honeycombs[J]. International Journal of Impact Engineering, 1983, 1(2): 157-174.

Finite Element Simulation Analysis on Out of Plane Static Compression of Paper-wood Honeycomb Board

CAO Min-naa, YANG Guo-chaob, ZHANG Qiu-huib

(a. Key Laboratory of Wood Material Science and Application, Ministry of Education b. Beijing Key Laboratory of Wood Science and Engineering, Beijing Forestry University, Beijing 100083, China)

The work aims to explore the collapse mode of paper-wood honeycomb boards and the deformation failure mode of a single honeycomb unit, so as to provide a theoretical basis for the internal failure mechanism of paper-wood honeycomb boards. Through finite element simulation, the out of plane static compression was analyzed and its deformation pattern, stress-strain pattern and stress-strain curve were obtained. The results showed that the compression process of paper-wood honeycomb boards was divided into four stages. The stress was concentrated in the honeycomb core layer. The outer most honeycomb deformed greatly first, and then the deformation of the middle honeycomb gradually increased. There was one or more stress peaks in the honeycomb core layer under compression. The honeycomb wall bent and folded for 1-2 times, generating 1-2 plastic hinges and absorbing energy in this process. In a word, the collapse failure trend of paper-wood honeycomb boards is from the outer honeycomb to the inner honeycomb, from the single wall to the double wall, and from the weakest collapse point to the rest.

paper-wood honeycomb board; honeycomb core layer; out of plane static compression; finite element

TS653.8、O242.21

A

1001-3563(2023)09-0199-07

10.19554/j.cnki.1001-3563.2023.09.024

2022?10?24

曹敏娜（1998—），女，碩士生，主攻紙木蜂窩板有限元仿真分析。

張求慧（1960—），女，博士，教授，研究方向主要為家具材料與包裝材料。

責任編輯：曾鈺嬋