輸入受限下的無人機編隊控制方法研究

盧帥多 胡盛斌

摘? 要： 針對多旋翼飛行器在軌跡跟蹤過程中控制輸入受限的問題，設(shè)計了一種控制輸入受限下的四旋翼無人機協(xié)同編隊分布式控制算法。首先，對于外環(huán)位置子系統(tǒng)，基于線性矩陣不等式的方法，設(shè)計了輸入受限下的多旋翼飛行器的編隊控制律，使得所有無人機的位置收斂到所需的編隊模式。其次，對于內(nèi)環(huán)姿態(tài)子系統(tǒng)，采用基于雙曲正切的方法設(shè)計控制輸入受限的控制律，使多無人機的姿態(tài)趨于一致。最后，基于 Lyapunov穩(wěn)定性理論，證明了系統(tǒng)的穩(wěn)定性，仿真結(jié)果表明，所設(shè)計的控制器能夠達到良好的協(xié)同跟蹤控制效果。

關(guān)鍵詞： 旋翼無人機； 編隊控制； 輸入受限； 線性矩陣不等式； 雙曲正切

中圖分類號：TP275? ? ? ? ? 文獻標(biāo)識碼：A? ? ?文章編號：1006-8228（2023）05-25-06

Distributed formation control for multiple quad-rotor under input constraints

Lu Shuaiduo， Hu Shengbin

（Shanghai University of Engineering Science， Shanghai 201620， China）

Abstract： Aiming at the problem of restricted control inputs in the trajectory tracking process of multi-rotor UAV， a distributed control algorithm for cooperative formation of quad-rotor UAV with restricted control inputs is designed. Firstly， for the outer loop position subsystem， based on the linear matrix inequality method， the formation control law of the multi-rotor aircraft under the input constraints is designed， so that the positions of all UAVs converge to the desired formation mode. Secondly， for the inner loop attitude subsystem， a method based on hyperbolic tangent is used to design a control law with constrained control input， so that the attitudes of multiple UAVs tend to be consistent. Finally， based on the Lyapunov stability theory， the stability of the system is proved， and the simulation results show that the designed controller can achieve a good cooperative tracking control effect.

Key words： UAV; formation control; input constraints; LMI; hyperbolic tangent

0 引言

近年來，四旋翼無人機發(fā)展迅速，相比于固定翼飛行器，其憑借體積小、結(jié)構(gòu)簡單、飛行方便等特點，在航拍、災(zāi)害監(jiān)測、地質(zhì)勘探等各個領(lǐng)域得到了廣泛的應(yīng)用。而在一些復(fù)雜和特定的環(huán)境中，多個無人機協(xié)同工作比單個無人機優(yōu)勢更明顯，但同時也對無人機編隊系統(tǒng)的穩(wěn)定性和一致性有更高的要求，目前多無人機系統(tǒng)的編隊問題逐漸成為無人機研究的重要方向。

四旋翼飛行器是典型的多輸入、多輸出、非線性、強耦合的欠驅(qū)動系統(tǒng)[1]。針對無人機編隊的隊形形制、編隊通信、一致性等問題，國內(nèi)外研究人員展開了深入的研究，提出了許多經(jīng)典編隊控制方法。目前，無人機編隊策略主要分為集中式策略和分布式策略。文獻[2]采用領(lǐng)航者-跟隨者的編隊方法，分別規(guī)劃好領(lǐng)航者和跟隨者飛行軌跡，實現(xiàn)無人機編隊。文獻[3]研究了具有非線性動態(tài)模型的多智能體系中的領(lǐng)導(dǎo)者和跟隨者的一致性問題。文獻[4]結(jié)合傳統(tǒng)的PID控制方法，設(shè)計了四旋翼編隊控制器。文獻[5]采用分布式模型預(yù)測控制和基于一致性的控制方法，實現(xiàn)了無人機編隊的協(xié)同編隊飛行。但是無人機編隊中的控制輸入受限問題仍然是一個難點，針對這一問題，文獻[6]對航天器設(shè)計了一種控制輸入及其變化率受限的姿態(tài)跟蹤控制器，可以克服航天器飛行過程中的不確定性和外部干擾，但設(shè)計參數(shù)過多。文獻[7]采用最優(yōu)控制策略設(shè)計了航天器的控制器，使控制輸入減小并保證系統(tǒng)的穩(wěn)定性，但此方法不能保證控制輸入在給定的范圍內(nèi)變化。

針對輸入受限情況下的多無人機編隊的一致性問題，本文的主要工作內(nèi)容如下：①基于圖論設(shè)計了分布式的無人機協(xié)同跟蹤控制問題，可以提高無人機的通信效率；②針對外環(huán)子系統(tǒng)，采用線性矩陣不等式的方法設(shè)計了控制輸入受限的控制器，使編隊系統(tǒng)的位置跟蹤達到一致；③針對內(nèi)環(huán)子系統(tǒng)，采用基于雙曲正切的方法設(shè)計了控制輸入受限的控制器，使編隊系統(tǒng)的姿態(tài)跟蹤達到一致；④采用Lyapunov理論證明設(shè)計控制律的穩(wěn)定性，并在matlab中進行仿真驗證所設(shè)計的編隊系統(tǒng)的有效性。

1 預(yù)備知識

在本節(jié)中，介紹了所需的基本概念和相關(guān)引理并給出了本文的問題描述。

1.1 圖論

圖通常用一個二元組[G=V，E]表示，其中[V=v1，v2，…，vn]表示有[n]個節(jié)點，邊集[E?V×V]表示為[vi，vj]，即尾節(jié)點[vi]和頭節(jié)點[vj]之間的連線，代表[vj]可以給[vi]傳遞信息，頂點[v]的入度是指以[v]為頭的弧的數(shù)目；頂點的出度是指以[v]為尾的弧的數(shù)目。圖[G]中節(jié)點之間的鄰接關(guān)系可以用鄰接矩陣[A=aijn×n]表示，其中[aij]表示節(jié)點[vj]到節(jié)點[vi]的權(quán)重。設(shè)矩陣[D=diagd1，d2，…，?n]，其中[?i=j=1naij]表示節(jié)點的加權(quán)入度。用圖[G]的拉普拉斯矩陣[L=D-A]，即入度矩陣[D]與鄰接矩陣[A]的差值來更清楚地描述節(jié)點之間的拓撲關(guān)系。無人機群編隊的期望軌跡為領(lǐng)導(dǎo)者的飛行軌跡，設(shè)[gi，?∈1，2…，n]表示第[?]個四旋翼無人機和領(lǐng)導(dǎo)者之間的連接權(quán)重，若第[?]架無人機與領(lǐng)導(dǎo)者之間有連接，則[gi>0]，否則[gi=0]，設(shè)矩陣[G=diagg1，g2，…，gn]。

1.2 相關(guān)引理

引理1 如下動態(tài)系統(tǒng)為全局漸進穩(wěn)定：

[x1=x2x2=-αtanhkx1+lx2-βtanhlx2]

其中，[α、β、k、l>0]。

引理2 存在一個閉環(huán)系統(tǒng)[x=IN?A-cL?BKx]，則此系統(tǒng)的穩(wěn)定性性質(zhì)等價于以下N階系統(tǒng)：

[A-cλiBK]

其中，[λi]為N階拉普拉斯矩陣L的特征值，[?=1，…N]。即它們有相同的特征值。

定理1 Schur補定理：假設(shè)C為正定矩陣，則[BC-1BT≤A]等價于[ABBTC≥0]。

2 問題描述

本文主要研究一組輸入受限情況下的四旋翼無人機的編隊控制問題。輸入受限是指無人機的控制輸入（升力、力矩等）不能無限大而是保持在預(yù)先設(shè)計好的有限范圍內(nèi)。假設(shè)一個有[n]個四旋翼的多智能體系統(tǒng)，[n]個四旋翼無人機之間的拓撲關(guān)系可以用圖G來描述，其中每個無人機對應(yīng)圖G中的一個節(jié)點。若一個節(jié)點的入度為零，則稱其為領(lǐng)導(dǎo)者，否則為跟隨者。一般來說，描述四旋翼無人機的信息由六個自由度變量組成，即外環(huán)的三個位置信息和內(nèi)環(huán)的三個姿態(tài)信息，其坐標(biāo)可以描述為：

[xi，yi，zi，?i，θi，ψiT∈R6，?∈1，2…，n]? ⑴

其中，[（xi，yi，zi）∈R3]是第[i]個無人機在空間中的的位置信息，[（?i，θi，ψi）∈R3]是描述無人機姿態(tài)的歐拉角。

2.1 無人機動力學(xué)模型

設(shè)有n架四旋翼無人機，則第[i]個無四旋翼人機的動力學(xué)模型可以描述為：

[xi=-K1mxi+cos?isinθicosψi+sin?isinψimu1iyi=-K2myi+cos?isinθisinψi-sin?icosψimu1izi=-K3mzi-g+cos?icosθimu1i?i=1Ixu2i+Iy-IzIxθiψiθi=1Iyu3i+Iz-IxIy?iψiψi=1Izu4i+Ix-IyIz?iθi] ⑵

其中，[xi]，[yi]，[zi]分別是無人機在地面坐標(biāo)系中沿三個軸的位移，[?i]是滾轉(zhuǎn)角，[θi]是俯仰角，[ψi]是偏航角。[m]表示無人機的質(zhì)量，[kjj=1，2，…，6]表示相應(yīng)的空氣阻力系數(shù)，[Ix]，[Iy，Iz]分別為系統(tǒng)繞三個軸的轉(zhuǎn)動慣量。[ui]是四個旋翼產(chǎn)生的總推力，[u2i]，[u3i]，[u4i]是四旋翼飛行器的旋轉(zhuǎn)動力。[g]是重力加速度。

2.2 控制目標(biāo)

四旋翼的編隊問題本質(zhì)上是跟蹤問題，對于外環(huán)子系統(tǒng)，定義期望的編隊軌跡[Xd=xd，yd，zdT]，即領(lǐng)導(dǎo)者的軌跡。定義領(lǐng)導(dǎo)者和跟隨者之間的軌跡偏差[epi=Xi-Xd-?i]，其中[Xi=[xi，yi，zi]T]表示第[i]個四旋翼飛行器的軌跡狀態(tài)。[?i=[?xi，?yi，?zi]T]表示第[i]個跟隨者與領(lǐng)導(dǎo)者之間的距離。設(shè)計合適的控制律并采用LMI的方法求出控制增益K，使得當(dāng)[t→∞]，跟隨者與領(lǐng)導(dǎo)者之間的位置誤差趨于零，控制輸入收斂到一定的范圍。

對于內(nèi)環(huán)子系統(tǒng)，定義領(lǐng)導(dǎo)者與跟隨者之間的姿態(tài)誤差[eai=Θi-Θdi]，其中[Θi=[?i，θi，ψi]T]，[Θi=[?di，θdi，ψdi]T]。采用輸入受限下的雙曲正切的方法設(shè)計合適的控制律，使得當(dāng)[t→∞]，跟隨者與領(lǐng)導(dǎo)者之間的姿態(tài)誤差趨于零。

3 系統(tǒng)設(shè)計

3.1 外環(huán)控制器設(shè)計

對于等式⑵，我們得到外環(huán)子系統(tǒng)如下：

[xi=-K1mxi+cos?isinθicosψi+sin?isinψimu1iyi=-K2myi+cos?isinθisinψi-sin?icosψimu1izi=-K3mzi-g+cos?icosθimu1i] ⑶

定義虛擬控制變量：

[τxi=cos?isinθicosψi+sin?isinψimu1iτyi=cos?isinθisinψi-sin?icosψimu1iτzi=-g+cos?icosθimu1i]? ⑷

則等式⑶可改寫為：

[xi=-K1mxi+τxiyi=-K2myi+τyizi=-K3mzi+ τzi]? ⑸

由于[x，y，z]三個方向的動力學(xué)模型結(jié)構(gòu)類似，因此我們以[x]軸的模型為例設(shè)計控制律。定義[x]軸跟隨者與領(lǐng)導(dǎo)者之間的軌跡誤差：

[expi=xi-xd-?xi]? ⑹

對等式⑹求導(dǎo)可得跟隨者與領(lǐng)導(dǎo)者之間的速度誤差：

[exvi=expi=xi-xd]? ⑺

則第[i]個無人機x軸方向的軌跡誤差定義如下：

[δxi=[expi，exvi]T]? ⑻

則可得系統(tǒng)狀態(tài)空間方程：

[δxi=010-K1mδxi+0τxi-xd-K1mxd=Axδxi+Bτxi] ⑼

其中，[Ax=010-K1m]，[B=01]，[τxi=τxi-xd-K1mxd]。

設(shè)計控制律為：

[τxi=-ck1j=1Naijexpi-expj+giexpi]

[-ck2j=1Naijexvi-exvj+giexvi]? ⑽

根據(jù)無人機之間的拓撲關(guān)系，外環(huán)子系統(tǒng)的控制律可改寫為：

[τx=-cL+G?Kxδx]? ⑾

結(jié)合式⑽和⑾，可得x軸方向的無人機閉環(huán)位置子系統(tǒng)：

[δx=（IN?Ax-cL+G?BKx）δx]? ⑿

其中，[?xi=0]，[G=diag（g1，g2，…，gN）]，[L]為通信拓撲圖的拉普拉斯矩陣，[IN]表示[N]階單位對角陣，[τx=[τx1，τx2，…，τxN]T]，[τx=[τx1，τx2，…，τxN]T]，[Kx=[kx1，kx2]]，[δx=[δx1，δx2，…，δxN]T]，[Kx]為需要LMI設(shè)計的反饋矩陣。控制目標(biāo)為通過設(shè)計LMI求解[Kx]，實現(xiàn)[δx→0]，[τ≤τmax]。

構(gòu)造Lyapunov函數(shù)如下：

[V=12δxTPδx]? ⒀

其中，[P>0，PT=P]。通過[P]的設(shè)計可有效地調(diào)節(jié)[s]的收斂結(jié)果，并有利于LMI的求解。

對式⒀求導(dǎo)得：

[V=12δx.TPδx+12δxTPδx.]=[12δxTHTP+PHδx]? ⒁

其中，[H=（IN?Ax-cL+G?BKx）]，令[Q=HTP+PH]。

為了實現(xiàn)指數(shù)收斂，即[V≤-αV]，取

[αV+V=αδxTPδx+δxTQδx=δxTαP+Qδx]

取[αP+Q<0]，[α>0]，則[αV+V≤0]，即[V≤-αV]，由不等式求解定理可解得：

[Vt≤V0exp-αt≤V0]

如果[t→∞]，則[Vt→0]，[δx→0]且指數(shù)收斂。

由于[V0=δT0Pδ0]，如果存在正定對稱陣[P]和[ω>0]，使得[sT0Ps0≤ω]成立，則可保證[V0≤ω]，即可保證[Vt≤ω]。

取[KxT?L+G2?Kx≤ω-1τ2maxP]，由[τx=-cL+G?Kxδx]可得：

[τx2=-cL+G?KxδxT-cL+G?Kxδx]

[≤c2δxTω-1τ2maxPδx]≤[c2τ2max]

則[τx≤cτmax]。

通過上述分析，構(gòu)造兩個LMI如下：

[αP+Q<0]? ⒂

[KxT?L+G2?Kx-c2ω-1τ2maxP≤0]? ⒃

根據(jù)引理2，可得[H]等價于[A-cλiBKx]，則可將式⒂中的[Q]展開如下：

[αP+（A-cλiBKx）TP+P（A-cλiBKx）]

[=αP+ATP+PA-cλiBKxTP-cλiPBKx<0]

其兩邊同乘[P-1]可得

[αP-1+P-1AT+AP-1-cλiP-1KxTBT-cλiBKxP-1<0]? ⒄

取[k0=c2ω-1τ2max]，則不等式線性化為[KxT?L+G2?Kx≤k0P]。

根據(jù)定理1，式⒃等價于：

[k0PKxTKx1≥0]

其左右兩邊同乘[P-1001]，可得

[k0P-1P-1KxTKxP-11≥0]? ⒅

令[F=KxP-1]和[N=P-1]，則[P-1KxT=FT]，則式⒄和式⒅可得第1個和第2個LMI：

[αN+NAT+AN-cλiFTBT-cλiBF<0]? ⒆

[k0NFTF1≥0]? ⒇

根據(jù)P的定義，可設(shè)計第3個LMI：

[P>0， P=PT]? （21）

要滿足[δT0Pδ0≤ω]，根據(jù)定理1，可將其設(shè)計為第4個LMI：

[ωδT0δ0N≥0]? （22）

通過這4個線性矩陣不等式，即式⒆-式（22），設(shè)計合適的[τmax]和[α]值，可求得有效的[K]。

同理，可設(shè)計第[i]個無人機的[y]軸和[z]軸模型的控制律：

[τy=-cL+G?Kyδy]? （23）

式（24）可改寫為

[τz=-cL+G?Kzδz]? （24）

3.2 內(nèi)環(huán)控制器設(shè)計

對于內(nèi)環(huán)姿態(tài)子系統(tǒng)：

[?i=Iy-IzIxθiψi+1Ixu2iθi=Iz-IxIy?iψi+1Iyu3iψi=Ix-IyIz?iθi+1Izu4i]? （25）

由式（25）可得

[Θi=MΘi+WTi]? （26）

其中，

[Ti=[u2i，u3i，u4i]T]，[M=0Iy-IzIxψi0Iz-IxIyψi00Ix-IyIzθi00]，

[W=1Ix0001Iy0001Iz]。

定義第[i]個無人機和期望姿態(tài)之間的誤差：

[ei=Θi-Θd]

則有

[ei=Θi-Θd]，[ei=Θi-Θd=MΘi+WTi-Θd]

其中，[Θi=?i，θi，ψiT∈R3]為慣性坐標(biāo)系中四旋翼飛行器的滾轉(zhuǎn)、俯仰和偏航姿態(tài)角，[Θdi=[?di，θdi，ψdi]T]為第[i]個無人機的期望姿態(tài)角。

令[e1i=ei，e2i=ei]，則

[e1i=e2ie2i=MΘi+WTi-Θd]? （27）

根據(jù)引理1，設(shè)計無人機的控制律為：

[Ti=W-1（-αtanhke1i+le2i-βtanhle2i-MΘi+Θd）] （28）

其中，

[α=α1000α2000α3]， [β=β1000β2000β3]，

[k=k1000k2000k3]， [l=l1000l2000l3]。

由式（30）可實現(xiàn)[e1i→0]，[e2i→0]，有

[|Ti|≤W-1（α+β-MΘi+max {Θd}）]? （29）

從而可控制輸入的受限，且控制輸入的幅度可由[α]和[β]調(diào)節(jié)。

式（28）系統(tǒng)穩(wěn)定性的證明如下：

設(shè)計Lyapunov函數(shù)為

[V=αlncoshke1i+le2i+βlncoshle2i+12ke22i] （30）

對式（30）求導(dǎo)得

[V=αke1i+le2itanhke1i+le2i+βle2itanhle2i-ke2ie2i]

令[t1i=tanhke1i+le2i]，[t2i=tanhle2i]，則[e2i=-αt1i-βt2i]，則上式可寫為

[V =-lαt1i+βt2i2-kβe2it2i]

由于[xtanhx=x?x-?-x?x+?-x≥0]，從而[V≤0]成立。當(dāng)且僅當(dāng)[e2i=e1i=0]時，[V=0]。即當(dāng)[V≡0]時，[e2i=e1i=0]。根據(jù)LaSalle不變性原理，系統(tǒng)式（29）為漸進穩(wěn)定，即當(dāng)[t→∞]時，[e1i→0]，[e2i→0]。系統(tǒng)的收斂速度取決于[α]， [β， k， l]。

4 仿真與分析

本節(jié)對前面推倒的編隊控制律進行驗證分析，設(shè)計無人機編隊模型如圖1所示，具有1架領(lǐng)航者無人機和4架跟隨者無人機。

有向邊的權(quán)重分別為：[b=1]，[a21=a32=a43=1]。圖1的拉普拉斯矩陣計算如下：

[L=0000-11000-11000-11]

事先給領(lǐng)航者無人機設(shè)計期望的編隊軌跡：

[xd=0.3t]， [yd=0.3t]， [zd=0.3t]， and [ψd=0.5]

仿真結(jié)果如圖2～圖7。

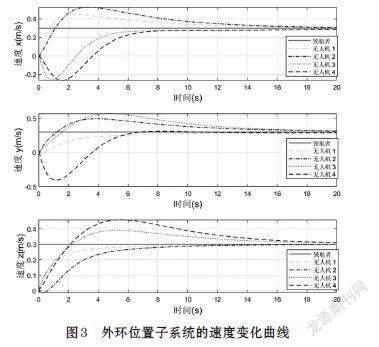
圖2和圖3顯示了外環(huán)子系統(tǒng)的仿真結(jié)果，采用LMI方法設(shè)計增益K的值，由分析可知，無人機的位移和速度逐漸收斂于期望值，領(lǐng)航者和跟隨者、跟隨者和跟隨者之間達到了期望值。

圖4和圖5為內(nèi)環(huán)姿態(tài)子系統(tǒng)的仿真結(jié)果，分析可知，4架跟隨者無人機經(jīng)過一定的時間后，姿態(tài)角度與姿態(tài)角速度逐漸與領(lǐng)航者無人機保持一致。

圖6為四架跟隨者無人機外環(huán)位置子系統(tǒng)控制律的變化，分析可知，采用上文的LMI方法設(shè)計的輸入受限的外環(huán)控制律，使系統(tǒng)的輸入值控制在了[[12.7，13.2]]的范圍內(nèi)，即控制律在有限的范圍內(nèi)浮動，并隨著時間的變化系統(tǒng)逐漸趨于穩(wěn)定。

圖7為四架跟隨著無人機滾轉(zhuǎn)角的控制律變化，分析可知，采用基于雙曲正切的輸入受限的內(nèi)環(huán)控制律，使?jié)L轉(zhuǎn)角的輸入值控制在了[-0.3，0.32]的范圍內(nèi)，并隨著時間的變化系統(tǒng)逐漸趨于穩(wěn)定。

5 結(jié)束語

本文針對輸入受限下的四旋翼無人機編隊一致性問題，基于圖論和一致性理論，設(shè)計了基于LMI和雙曲正切方法的控制輸入受限的分布式編隊控制律，采用Lyapunov穩(wěn)定性理論證明了系統(tǒng)的穩(wěn)定性，最終實現(xiàn)了多無人機的協(xié)同跟蹤控制，并在Matlab中仿真驗證了所設(shè)計的控制律的正確性。結(jié)果表明，本文所提的方法可以有效使無人機編隊系統(tǒng)趨于穩(wěn)定，并使系統(tǒng)的控制輸入有界。

參考文獻（References）：

[1] Lim， H， Park， et al. Build Your Own Quadrotor： Open-

Source Projects on Unmanned Aerial Vehicles[J]. IEEE robotics and automation magazine： A publication of the IEEE Robotics and Automation Society，2012

[2] Turpin M，? Michael N， Kumar V. Trajectory design and

control for aggressive formation flight with quadrotors[J]. Autonomous Robots，2012，33（1-2）：143-156

[3] Jianan， Wang， Ming， et al. Integrated Optimal Formation

Control of Multiple Unmanned Aerial Vehicles[J]. Control Systems Technology，2013，21（5）：1731-1744

[4] GosiewskiZ ，Ambroziak L . Formation Flight Control

Scheme for Unmanned Aerial Vehicles[J]. Lecture Notes in Control & Information Sciences，2012，422：331-340

[5] Toru， NAMERIKAWA， Yasuhiro， et al. Formation Control

with Collision Avoidance for a Multi-UAV System Using Decentralized MPC and Consensus-Based Control[J]. Sice Journal of Control Measurement & System Integration，2015

[6] Zou A M，? Kumar K D，? Ruiter A H J D. Robust attitude

tracking control of spacecraft under control input magnitude and rate saturations[J]. International Journal of Robust and Nonlinear Control，2016，26（4）

[7] Guo Y，? Guo J H，? Song S M. Backstepping control for

attitude tracking of the spacecraft under input saturation[J]. Acta Astronautica，2017，138（sep.）：318-325