人工智能在船舶航行數學建模中的應用
白 靈,趙珈玉,鞠巖松
(1. 長春電子科技學院 光電科學學院,吉林 長春 130000;2. 長春理工大學 化學與環境工程學院,吉林 長春 130000)
0 引 言
船舶在航行過程中,會遇到海面勘探、石油開發等水域作業情況,為使船舶安全航行,規劃其航行航線意義重大。楊琪森等[1]提出的船舶路徑規劃與避障方法,該方法通過構建馬爾可夫決策過程抽象模型,通過深度強化學習算法,規劃了船舶航行路徑。謝新連等[2]提出復雜水域船舶路徑規劃方法,該方法建立環境模型,分析海浪對船舶速度的影響,利用改進粒子群算法優化船舶航行路徑。上述2 種方法雖可實現船舶航線優化,但優化結果不夠準確。人工智能算法也被稱為機器學習算法,其包含尋優算法、識別算法等多種算法[3],是求解目標函數算法,可通過反復迭代輸出最優解。面對當前船舶航線優化算法存在的不足,研究人工智能在船舶航行數學建模中的應用,為船舶導航提供技術支持。
1 基于人工智能的船舶航行數學建模
1.1 船舶航線規劃數學模型構建
海上鉆井平臺或勘探區域作業通常包含多個水上、水下作業點,船舶在該區域航行時,受其作業點影響,威脅其航行安全[6],因此船舶航行時需規避海上不同作業點。
在建立船舶航線優化模型之前,使用Maklink 圖論方法描述海上作業點分布,在海上作業水域建立Maklink 連接圖,利用該圖描述船舶在作業水域內可航行網絡圖,并將其表述為可求解的數學模型。令S和T分布表示船舶航行起點和終點,在點S和T之間的航線點序列 {S,q1,q2,···,qk,T}構成,在該點序列內,排除船舶航行起點和終點之外,其中包含的點均存在轉向的可能。當船舶航行速度為定值情況下,使用 θqi表示船舶在點位置的轉向角, φmax表示船舶在其設計航速下的轉向極限角數值。船舶在轉彎時,需考慮其轉彎半徑[7],船舶航速為10 kn 時,其最小轉彎半徑和轉向角參數如表1 所示。

表 1 船舶最小轉彎半徑參數設計Tab. 1 Parameter design of minimum turning radius of ship
令Vt表示船舶航行速度,R表 示大型船舶航道轉彎半徑,當船舶為10×104~15×104t 的大型貨輪時,其航道轉彎半徑計算公式如下:

式中:θ 表示船舶在某個點的轉向角度;L表示船舶長度。
在綜合考慮船舶轉向角度和轉彎半徑后,建立船舶在海上作業區域航線規劃數學模型,其表達公式如下:
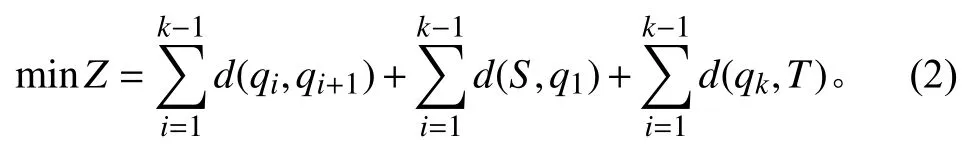
式中: minZ表示船舶在海上作業區域航線規劃目標函數;(qi,qi+1) 為 由 點qi和qi+1兩 點 組 成 的 航 線 段;d(·)表示航線點之間距離;(S,q1)表 示船舶起點S到q1航線點之間的航線段;(qk,T) 為船舶航線點qk到終點T之間的航線段。
令k表示船舶航行路徑終點前的一個點,Z和Zmin分別表示航線與危險區域最小距離和最小安全距離。設置公式(2)約束條件為:

式中:l(qi,qi+1)表 示由qi和qi+1兩點連接組成的航線點集,該點集與作業危險區域點集S j的交集為空集;船舶 航 行 時 節 點 θqj∈(1,2,···,k)的 轉 角 需 小 于 φmax;λ表 示 船舶最小轉彎半徑和船舶長度比值。
經過上述步驟,完成船舶航線規劃模型構建。
1.2 基于Dijkstra 算法的船舶航線規劃模型求解
通過構建船舶在海上作業危險區域航線規劃模型,利用Dijkstra 算法求解該模型,獲得船舶在海上作業區域初始航線,其詳細過程如下:
將求解船舶在海上作業危險區域航線規劃模型問題轉換成有向圖最短路基問題[8],利用圖論方式描述該模型,令W表示有向弧權值集合,則其船舶在海上作業危險區域航線規劃模型圖論表達公式如下:

式中:G表示船舶航線規劃有向圖;V=(v1,v2,···,vn)
表示航線有向圖頂點集合;A表 示頂點之間有向弧集合。
利用Dijkstra 算法求解船舶在海上作業危險區域航線規劃模型步驟為:
步驟1對航線有向圖頂點V=(v1,v2,···,vn)賦予2 個標號 (U,E) ,U表示臨時標號,該標號為實數,用于描述定點路徑長度,E表示永久標號,描述有向弧的起始點。


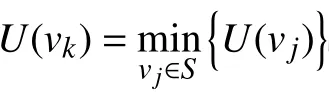
步驟5當vk=vn時 ,則得到航線點的最小距離E(vk)。
經過上述步驟,得到船舶在海上作業區域初始航線。
1.3 基于人工智能算法的船舶初始航線優化方法
使用Dijkstra 算法求解船舶在海上作業危險區域航線規劃模型,得到其初始航線時,受航線點數量較多影響,其生成的初始航線無法滿足船舶航行時的機動性能,因此以船舶在海上作業危險區域初始航線為基礎,使用人工智能算法內的蟻群優化算法對船舶初始航線優化處理。
將船舶航行初始航線上的節點賦予初始值,生成初始信息素矩陣,其中危險區域節點的初始值為0,其他節點初始值為1。當時刻為t時,蟻群移動到線段Li位置。令第k只螞蟻在點a(xi,yg) 位置,ηab(t)表示點a和b之 間的能見度,bj為線段Li+1上 的節點,ψ (j)為時刻為t時 ,節點j上殘留的信息素。螞蟻k在運動時,每個路徑上的信息素決定其移動方向。在時刻為t時 ,螞蟻k從a(xi,yg) 處轉移到b(xi+1,yi)處的概率計算公式如下:

式中: α表示信息素相對重要性;ρkab表示螞蟻k從a(xi,yg) 處 轉 移 到b(xi+1,yi) 處 的 概 率;? 和 ?′分 別 表 示航線安全區域和風險區域;β能見度相對重要性。
螞蟻依據公式(7)概率搜索,在搜索過程中按照下式全局更新規則更新其行走路徑:

式中: ?表示信息素蒸發因子;? ψ(j)表示全局更新因子,其計算公式如下:

式中:h表示螞蟻總數;Q表示常數;Jk表示螞蟻搜索到可航行路徑目標函數。
蟻群按照公式(9)更新其路徑后,當迭代次數達到閾值次數,則輸出當前路徑,該路徑即為優化后的船舶在海上作業區域航行路徑,利用該路徑為船舶導航,保障其安全航行。
2 實驗分析
以某中型貨運船舶作為實驗對象,其需穿越海上石油鉆井平臺作業區域,其作業區域分布以及船舶航行起點位置如圖1 所示。

圖 1 海上作業區域與船舶航行起點Fig. 1 Offshore construction area and ship navigation starting point
2.1 作業水域可航行網絡圖
生成海上作業區域可航行網絡圖是獲得船舶初始航線和航線優化的基礎,使用本文方法獲取海上作業區域,作業水域可航行網絡如圖2 所示。

圖 2 作業水域可航行網絡Fig. 2 Navigable network of construction waters
可知,本文方法可有效依據海上石油鉆井平臺作業區域得到船舶可航行線路,生成船舶可航行線路網絡圖,為后續得到船舶初始航線與初始航線優化打下良好基礎。
2.2 船舶初始航線生成與航線優化
使用本文方法生成該船舶從起點到目的地航線,并對該航線優化處理,初始航線生成與航線優化結果如圖3 所示。

圖 3 初始航線生成與航線優化結果Fig. 3 Initial route generation and route optimization results
可知,使用本文方法可有效生成該船舶航行的初始航線,但該初始航線需要多次變更航向才可到達目的地,且生成的初始航線穿過7 號、8 號作業區域與11 號作業區域,該3 個作業區域呈三角形分布,中間航道較為狹窄,影響船舶航行航速。而使用本文方法對該初始航線優化后,優化后的航線僅需變更一次航向即可到達目的地,同時航行穿越作業區域時,其航道較寬,船舶可安全航行。綜上結果,本文方法可有效生成船舶航行初始航線,并使用人工智能算法對其優化處理,具有較好的應用效果。
3 結 語
為了保證船舶的安全航行,研究人工智能在船舶航行數學建模中的應用方法。通過建立船舶航行數學模型并求解后,得到船舶航行初始航跡,通過人工智能算法中的蟻群算法,對其初始航跡優化,使船舶航行更加安全。通過對本文方法實際驗證,其在生成船舶航線網絡圖,得到初始航線并優化方面均具備較好的能力,可用于船舶穿越海上作業區域導航,為船舶安全航行提供保障。

