基于可靠性的索穹頂結構優化設計
陳聯盟,李澤斌,章 禾,劉毅杰,周一一,董石麟
(1. 溫州大學 建筑工程學院,浙江 溫州 325035; 2. 常州工學院 土木與建筑學院,江蘇 常州 213002;3. 浙江大學 空間結構研究中心,浙江 杭州 310027)
0 引言
索穹頂結構是一類基于Fuller整體張拉思想、由拉索和壓桿為基本單元、通過張拉成形的自平衡柔性空間結構。由于能充分利用拉索的高強性,且能通過施加和優化預應力分布來提供和優化結構剛度,故該類結構具有跨度大、構造輕盈、形態優美、經濟性能卓越等諸多優點,在實際工程中得到廣泛應用,目前主要包括Geiger型和Levy型兩類索穹頂結構類型。然而實際工程中,Geiger型索穹頂結構由于索桁架平面外剛度較弱,且結構冗余度低,在不對稱荷載作用下容易失穩[1];Levy型索穹頂結構對施工誤差敏感,使得結構實際狀態與理想狀態存在一定偏差,進而影響結構承載性能[2-3]。另外隨著社會的不斷發展,以索穹頂結構為代表的索桿張力結構在各種極端環境條件下各種倒塌情況時有發生。1978年美國Hartford公民中心體育館的屋蓋結構以及2010年美國明尼蘇達Minnesota Vikings 索膜結構體育館均因暴風雪極端天氣發生整體倒塌事故。因此,為保證該類結構在各種荷載條件下具有足夠的安全性、耐久性和適用性,需通過合理設計保證其具有足夠的可靠性。
可靠度是反映結構可靠性的指標,其思想可以追溯至19世紀初,當時常使用基于實際經驗的安全系數來確保結構的正常工作[4],其本質上是對實際工程中各種不確定因素的綜合估計。到了20世紀初,工程界基本確立了使用概率論反映客觀存在的隨機變量,并以此度量結構可靠度的研究路線。MAYER[5]首次系統闡述了使用概率論分析結構可靠度的思路。隨后FREADENTBAL[6]、LIND[7]等學者進一步發展了結構可靠性理論并進入實用階段。趙國藩[8]較早地采用數理統計的方法研究了荷載、材料強度的概率分布及基于可靠度理論的結構極限狀態設計方法。因此,基于可靠度的結構性能分析理論以及在此基礎上構建的工程設計方法是目前非常基本又非常重要的分析方法[9-10]。
當前索穹頂結構的優化設計一般集中在4個層面,即預應力優化[11-12]、截面優化[13]、形狀優化[13-14]及拓撲優化[14-15],其中截面優化、形狀優化及拓撲優化設計多圍繞著結構質量最輕這一優化目標展開。實際上,索穹頂結構的自重本身就較輕,用鋼量一般不到30 kg/m2,對其進一步進行質量優化意義不大;另一方面,隨著社會的不斷發展,面對更為復雜的結構形式、更為極端的氣候條件,對于索穹頂結構自身的各項性能必然有著更為嚴格的要求。因此,開展基于結構性能(如可靠性)的優化設計,對于索穹頂結構的進一步推廣應用具有較強的理論研究和工程應用價值。
文中從可靠性角度出發,首先提出基于索穹頂結構非線性特性的結構可靠度量化評價指標,結合Geiger型索穹頂結構模型,分析構件截面積對結構可靠度的影響規律;然后使用遺傳算法,在不增加結構質量的前提下開展基于結構可靠性的截面優化設計;在此基礎上,基于提高結構冗余度的優化理念,進一步提出一種布索優化方案以提高結構整體可靠性;最后再次使用遺傳算法,對布索優化方案下的索穹頂結構進行截面優化設計,尋求最優的結構形式和材料分布,因此文中的研究具有較高的理論研究和工程應用價值。
1 索穹頂結構可靠性分析方法
1.1 索桿體系可靠度計算方法
工程中常采用可靠性框圖法來描述系統可靠性。分析時,首先根據Maxwell準則,判斷結構是串聯系統、并聯系統還是同時具有串聯和并聯系統。如果拆除任意桿件均會引起結構變成可變體系,則該體系為串聯系統,此時結構整體可靠度為:
(1)
式中,pi為第i根桿件的可靠度。如果只要有一個單元正常工作,整個系統便能正常工作,則該系統為并聯系統,此時結構整體可靠度為:
(2)
式中,Xf,i為第i個單元的失效概率。如果結構中既有串聯系統又有并聯系統,即表決系統,則在由n個單元組成的系統中,只有當至少k個單元正常工作時,整個系統才能正常工作,此時結構可靠度為:
(3)
式中,Xj為第j個單元正常工作的概率。
1.2 索穹頂結構桿件可靠度計算方法
文中主要基于一次二階矩理論中的中心點法來計算桿件可靠度,即:
pi=Φ(βi)
(4)
式中:函數Φ(x)為標準正態分布函數;βi為單根桿件的可靠指標,其計算方法為:
(5)
式中:μr,i、μs,i分別為第i根桿件強度與應力的平均值;σr,i、σs,i分別為第i根桿件強度與應力的標準差。μr,i的取值可以參考《鋼結構設計規范》中的相關規定,μs,i值可通過讀取各桿件的應力值再對其求平均值得到。σr,i采用式(6)求得,
σr,i=cv×μr,i
(6)
式中,cv為變異系數,文中荷載、拉索類桿件強度及壓桿類桿件強度的變異系數分別取0.074、0.08和0.047[16]。另外,雖然荷載服從正態分布,但由于索穹頂結構為非線性結構,故σs,i與us,i之間的關系無法直接通過簡單的線性關系式得出,需使用以下方法計算σs,i值。
假定結構實際承受荷載F(t)為常規設計荷載值P與荷載干擾值w(t)之和,即:
F(t)=P+w(t)
(7)
式中,干擾值w(t)服從 (0,σp)的正態分布,則F(t)服從(P,σp)的正態分布。根據概率論中的“3σ”法則:盡管真實荷載的取值區間為(-∞,+∞),但在區間(P-3σp,P+3σp)發生干擾的概率達99.74%。因此,在施加干擾值時,可以近似的將干擾值限定在(-3σp,+3σp)之內。進一步將荷載干擾值的區間分為m段(為方便計算,m一般取偶數,文中取100),由于其關于y軸對稱,故以下只討論區間(-3σp,0)上的情況。
取每個區間上的中點值近似表示該區間上的荷載干擾值大小,則第k個區間為(3σp·(k-1)/(m/2),3σp·k/(m/2),該區間上的荷載干擾值大小為3σp·(2k-1)/m, 0 (8) 對該區間上的概率密度函數積分作為第k個區間的權重系數Q(k), (9) 則σs應力標準差的計算公式為: (10) 式中:uk,i為干擾值發生在第k個區間上時,第i根桿件的應力大小;當干擾值發生在區間(0,+3σp)上時,σs,i的計算原理與上述完全相同,這里不再贅述。 結合Geiger型索穹頂結構案例,分析結構可靠度及桿件截面對結構可靠性能的影響規律。結構跨度71.2 m,矢高5.5 m,環向16等分。結構設置一道環索,中心設置拉力環。結構支座為固定鉸支座,設計荷載0.4 kN/m2。結構剖面圖如圖1所示,構件材料參數以及初始預應力[17]如表1所示。拉索和壓桿彈模分別為160、206 GPa。 圖1 結構剖面尺寸Fig. 1 Structure section and dimensions 模型包含144根桿件,分為外脊索、內脊索、外斜索、內斜索、外壓桿、內壓桿、外環索、內下環索、內上環索共9個子系統。其中,內下環索與內上環索同屬于內環索類桿件,為簡化方便起見,文中分析時兩者的截面積均保持一致,統稱內環索。 分別計算各類型桿件在不同截面積(0.8、1.0、1.2、1.5倍初始截面)時結構整體可靠度,結果如表2所示,可見:1)外脊索、內脊索、外斜索、內斜索、外壓桿、內壓桿、外環索、內環索8類桿件截面由初始大小增大到1.5倍截面積時,結構整體的可靠度分別提高了13.88%、7.33%、0.52%、12.16%、-0.28%、-0.03%、-8.39%、0.06%,負值表示減小,表明不同桿件的截面變化對結構整體可靠度產生不同的影響。2)增大脊索類與斜索類桿件截面時,結構整體可靠度總體上會增大。3)而增大壓桿類與外環索截面積時,會使結構整體可靠度減小,原因是對于壓桿來說,其在初始截面時桿件可靠度已達上限1,增大壓桿截面將增加結構整體質量,增大其余桿件的工作負擔,進而導致結構整體可靠度下降;對于外環索來說,雖然增大截面積可以提高構件可靠度,但是由于外環索的桿件長度較長、截面較大,故增大其截面將會使結構增加較多質量,使得其它桿件的可靠度出現不同程度的減小,從而導致結構整體可靠度減小。 基于前文分析的各類桿件截面面積變化對于結構可靠度具有不同的影響規律,本節進一步對上述Geiger型索穹頂進行基于結構可靠性的截面優化設計。在優化分析中,直接基于ANSYS軟件中的零階和一階優化算法適用于線性結構,而對于非線性結構其準確性會大大降低,而遺傳優化算法采用生物仿生進化原理,具有與問題領域無關的全局搜索能力,且計算準確度高,故文中采用遺傳算法對結構進行截面優化分析與設計,基本思路為: 1)使用Matlab編寫遺傳算法主程序,設置初始參數,確定優化目標并選擇優化變量,限定優化變量的取值范圍,并采用二進制編碼生成初始種群。文中,種群大小設為15,字符串長度設為32,交叉概率為0.8,變異概率為0.2,進化迭代次數設為300次。 2)將生成的種群導入有限元分析軟件ANSYS,建模并計算種群內所有個體的適應度值,即結構可靠度。計算得到的適應度值個數應與種群內個體數相等。 3)將ANSYS計算結果導入Matlab,對適應度值按最大值進行排序,提取初始種群中的最佳個體,并對其進行復制、交叉和變異,以此進行循環迭代計算,直至迭代次數達到設定值。 優化的具體過程如圖2所示。 圖2 遺傳算法優化流程示意圖Fig. 2 Schematic diagram of genetic algorithm optimization process 文中探索結構總質量不增加前提下,通過優化桿件截面和材料分布,使得結構整體可靠度盡可能大,即探索Psys值最大,優化目標為maxPsys。各類桿件截面大小變化范圍為初始截面值的0.8~1.2倍,且荷載作用下應力不能超過屈服點。其數學優化模型可表示為: (11) 截面優化迭代過程如圖3所示,優化結果如表3所示,可見,1)優化迭代到170次后基本達到穩定,優化后整體可靠度由0.728 123提高到0.891 355,優化率達22.4%。2)外脊索、內脊索、外斜索、內斜索及外環索桿件面積分別增大了1.35%、9.33%、1.33%、11.99%和6.70%,內壓桿、外壓桿及內環索桿件面積分別減小20.0%、17.36%和1.34%,該變化現象總體上與前面參數分析時各類桿件截面變化對于結構可靠度的影響規律相一致。3)文中同時計算分析了結構質量不約束時截面優化設計后結構整體可靠度為0.998 795,優化率達37.2%,即優化過程中無質量約束可進一步提高結構可靠度。 圖3 截面優化迭代過程Fig. 3 Iterative process of cross section optimization 表3 截面優化前后不同桿件截面積及可靠度Table 3 Different bar cross-sectional area and reliability before and after section optimization 通過分析可以發現,該Geiger型索穹頂結構整體冗余度較低,各個子系統及子系統內的桿件均以串聯的邏輯聯結在一起,以至于結構中微小的損傷會較大程度地影響整體可靠度,因此,文中以改變子系統內桿件的邏輯聯系、提高整個結構的冗余度為布索方案優化設計出發點,將原結構外圈徑向布置的外脊索和外斜索布置方式調整為Levy型,桿件面積為原桿件面積0.6倍,形成內圈Geiger-外圈Levy型的復合型索穹頂。優化后的結構模型如圖4所示。 可以發現,外脊索與外斜索的桿件數均由16根增加到了32根。根據Maxwell準則,該結構的冗余度r=b+k-3j=176+3×16-3×64=32,與優化前的模型比較,其冗余度大幅提高。重新計算布索方案優化后各類桿件的可靠度及結構整體可靠度,計算結果見表4,可見:1)對結構布索優化方案進行調整后,結構整體可靠度由0.728 123提高至0.862 487,優化率達18.5%。2)對布索優化方案進行調整后,結構整體自重略微增加,雖然大部分桿件的可靠度并無明顯的變化,但由于結構整體冗余度大幅提高,各子系統內部聯結邏輯也發生了改變,以至于結構整體的可靠度明顯提高,因此該方案是一種可行、有效的優化方案。3)作者同時研究了其他提高結構冗余度的布索優化方案,發現同樣可有效提高結構可靠度。 (12) 優化迭代過程如圖5所示,優化結果如表5所示,可見,1)優化迭代到180次后基本達到穩定,截面優化后結構整體可靠度由0.862 487進一步提高至0.997 676,優化率達15.7%。2)優化后,外斜索和壓桿類桿件截面減小,其余各類桿件截面積均增大。其中,外壓桿和內壓桿的截面變化最大,均達到桿件截面變化臨界值-20%;其次為內斜索、內脊索、內環索和外斜索,分別為17.3%、12.0%、12.0%和-12.0%;外脊索和外環索的截面變化最小,分別為6.7%和9.4%。3)文中同時計算分析了優化過程中不控制結構質量時優化后結構整體可靠度為0.999 630,優化率為15.9%。 圖5 質量約束布索-截面綜合優化迭代過程Fig. 5 Iterative process of mass constraint cable-cross section synthesis optimization 表5 質量約束布索-截面綜合優化前后不同桿件截面積及可靠度Table 5 Different cross sectional areas and reliability of bars before and after mass constrained cable-section optimization 文中針對索穹頂結構缺乏有效的基于結構性能優化設計理論現狀,以可靠度理論為基礎,提出了基于一次二階矩理論中心點法的索穹頂結構非線性可靠度分析方法,并結合Geiger型索穹頂模型開展了結構可靠度分析、截面優化設計、布索優化設計及布索-截面綜合優化設計等,得出如下結論: 1)不同類型桿件截面面積的變化,導致結構整體可靠度呈現出不同的變化趨勢; 2)控制結構質量不增加前提下,索穹頂結構截面優化后,結構可靠度由0.728 123提高到0.891 355,優化率為22.4%; 3)布索方案優化使結構可靠度由0.728 123提高至0.862 487,優化率為18.5%; 4)控制結構質量不增加前提下,對索穹頂結構進行布索-截面綜合優化,結構整體可靠度由0.862 487進一步提高至0.997 676,優化率為15.7%,因此開展合理的截面優化和布索優化設計可有效提高結構整體可靠度。 綜上,文中基于可靠性的分析、評價及優化設計理論具有一定的理論研究和工程應用價值。2 索穹頂結構可靠性分析



3 截面優化設計
3.1 優化算法

3.2 優化模型
3.3 優化結果

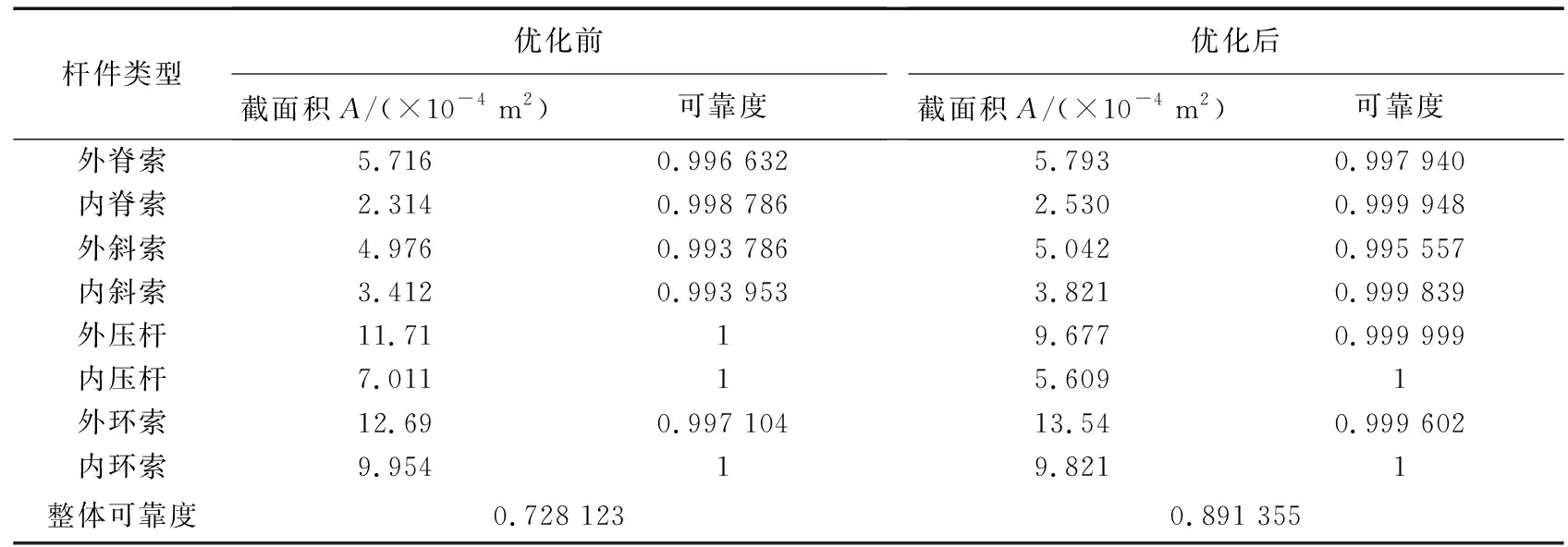
4 布索方案優化設計


5 布索-截面綜合優化設計
5.1 優化模型

5.2 優化結果


6 結語

