發動機燃燒室中火焰對來流擾動的動態響應研究綜述

楊立軍，劉曉康，田 雨，姜霄震，李敬軒

(1. 北京航空航天大學宇航學院，北京 100191；2. 北京航空航天大學寧波創新研究院先進飛行器與空天動力創新研究中心，寧波 315800)

0 引 言

隨著新一代空間站建造的深入,以及探月計劃和火星探測計劃的進一步開展,中國對大推力液體火箭發動機的需求不斷增加。此外,隨著國內外環保法規的日益嚴苛,貧燃燃燒、低NOx排放的航空發動機正在成為民用航空動力的主流,與之相對應的地面燃氣輪機也同樣朝著貧燃燃燒的方向發展。然而不管是大推力的火箭發動機還是貧燃燃燒的航空發動機、地面燃氣輪機,都已經廣泛觀察到了熱聲不穩定現象[1-3]。

發生熱聲不穩定的本質是不穩定燃燒過程導致的熱釋放率脈動、火焰上游來流的速度擾動以及燃燒室聲學系統中的聲波振蕩之間的非線性耦合[4-6]。根據Rayleigh準則,當燃燒室內的壓力脈動和熱釋放率脈動之間的相位小于90°時,火焰會給整個燃燒室聲學系統提供能量,這是發生熱聲不穩定的驅動源。但受黏性、熱傳導以及聲輻射的影響,整個聲學系統的能量會因此衰減。當驅動系統振蕩的能量大于系統耗散的能量時,熱聲不穩定便會產生。這會導致燃燒裝置的性能下降,嚴重時會使其損壞并失效。總而言之,熱聲不穩定具有形成機理復雜且危害大等特征。

確定火焰熱釋放率對流動擾動的脈動響應是理解和預測熱聲不穩定現象的關鍵環節之一。火焰受到來流速度擾動的影響,會以熱釋放率脈動的響應形式呈現。根據擾動幅值的大小可將火焰對其響應分為兩種不同情況,線性響應和非線性響應。當來流擾動的幅值較小時,可以認為火焰對輸入信號的響應是線性的,此時火焰的響應只與施加擾動的頻率相關,這種線性響應規律可以使用火焰傳遞函數(FTF)來量化[7],并以無量綱熱釋放率脈動和無量綱速度擾動的比值來定義FTF。當來流速度擾動的幅值足夠大時,其幅值對火焰響應的影響無法忽略,這個過程需要使用火焰描述函數(FDF)來確定,此時火焰通常會呈現出非線性飽和效應[8],即隨著來流擾動幅值的增強,火焰響應會趨于飽和。

1 FTF/FDF研究進展

目前對FTF/FDF的研究主要從三個方面展開,分別是實驗測量、數值仿真以及解析推導。

1.1 問題提出

對于火焰傳遞函數的實驗測量,一般將火焰視為一個整體,通過上游給定調制的速度擾動信號,使用化學發光[9-13],激光干涉[14]或超聲波飛行時間差[15]等方法來實現對火焰熱釋放率脈動的精確動態測量。以化學發光法為例,一般使用配備CH*或OH*自由基濾光片的光電倍增管或高速相機對火焰的動態發光強度進行獲取,并根據層流預混或弱湍流預混火焰的發光強度波動和熱釋放率脈動之間的線性定量關系獲得FTF/FDF。速度擾動則使用激光多普勒測速法、粒子圖像測速法以及多麥克風法等方法獲得。給定FTF/FDF計算公式如下:

(1)

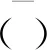
在早期研究中,Ducruix等[11]對層流預混錐形火焰的FTF進行了實驗測量,結果表明,火焰鋒面的脈動幅值明顯依賴于上游施加的擾動頻率,且火焰對來流擾動頻率的響應呈現低通濾波特性且存在截止頻率。Noiray等[10]基于一個在火焰上游的可變長度共振腔試驗系統對多孔板甲烷-空氣預混小火焰進行FDF測量,結果如圖1所示。分析測量結果可以發現隨著來流擾動幅值的增加,FDF的幅值會下降,火焰對擾動的響應呈現非線性飽和效應,但是FDF相位變化并不明顯。

圖1 FDF實驗結果[10]Fig.1 FDF experimental results[10]

Durox等[13]測量了錐形、V形、M形以及多錐形層流預混火焰的非線性響應特性,通過分析4種火焰類型的FDF測量結果發現不同火焰類型的FDF差異較大。具體而言,在低頻段,單錐形火焰FDF的幅值受來流擾動幅值的影響較弱,且相位隨著頻率線性變化;但在高頻下相位隨著頻率的增加會出現飽和;其次,V形和M形火焰FDF的幅值在中頻下會超過1,此時FDF幅值隨著來流擾動幅值的增加而下降,而相位受來流擾動幅值的影響不明顯,且隨著頻率的改變會呈現出準線性特性;最后,多錐形火焰的FDF幅值在較窄頻段內超過1,且其受來流擾動幅值影響而減小的特性隨著頻率的提高而變得明顯;FDF相位的斜率會隨來流擾動幅值的增加而輕微變大,但其在頻率變化過程中仍然呈現出準線性的特征。總而言之,火焰結構等特性會強烈影響火焰的非線性響應特性。

FTF/FDF測量關鍵是熱釋放率的測量,然而傳統的基于化學發光法的測量方法通常局限于層流預混火焰。Li等[14-15]創新地提出了兩種實驗測量FTF的方法。首先,克服了光學測量方法直接測量熱釋放率的限制,發展了一種新型的超聲波測量火焰熱釋放率的方法[15],通過測量超聲波在所測區域內飛行時間變化來捕捉火焰前鋒面的運動軌跡,最終量化火焰熱釋放率脈動以計算FTF,結果表明該方法具有較強的創新性和適用性。其次,基于燃燒熱釋放率變化與密度變化的關系發展了使用激光干涉法測量密度變化進而量化火焰熱釋放率脈動的方法[14]。這種方法可以擺脫傳統化學發光法只能測量層流預混或弱湍流預混火焰的局限性,此方法的成功實驗意味著湍流擴散火焰熱釋放率脈動的測量成為可能。

最近,Wang等[9]針對具有上游聲學擾動的旋流預混穩定火焰的FTF幅值和相位分別進行了測量,發現了幅值隨著驅動頻率的變化和相位對頻率的導數隨頻率的變化高度一致,幅值和相位導數在關于頻率的函數中本質上是線性關系,這就意味著FTF的幅值和相位并不是相互獨立的。針對這一現象,他們發現可以使用解析分解的方法對其進行解釋。周期振蕩旋流火焰的FTF可以認為是所有擾動機制的復雜矢量,通過矢量分解將FTF結果分解為二矢量模型,進而很好地解釋了幅值和相位導數的同步變化特性。

1.2 仿真研究

為進一步理解FTF/FDF內在機制以及探究在復雜情況下火焰對上游擾動的響應機理,科研人員通過仿真方法進行了深入研究。

為了更深入地認識旋流湍流預混火焰的非線性響應飽和現象,Krediet等[16]基于大氣環境下旋流穩定的湍流預混火焰的實驗結果進行了大渦模擬,探究其響應的飽和機制并與已有文獻的實驗結果[17]相比較。他們通過在燃燒室進口邊界條件處施加單頻率的諧波,通過改變施加諧波的幅值和頻率來獲得FDF,得到的結果和文獻實驗結果[17]吻合較好。此外他們對旋流預混火焰的研究結果表明,火焰鋒面面積隨著來流擾動幅值增加而出現的非線性演化現象是導致火焰出現非線性響應特性的主要原因。對結果進一步分析發現,在引起火焰非線性響應的上游速度擾動中,主要是軸向方向上的速度擾動起作用,而與周向速度擾動的關系不大。

Han等[8]針對鈍體穩定湍流預混火焰使用結合火焰面密度和分型方法來模擬湍流中的褶皺因素,并據此發展了一種開源大渦模擬方法來探究湍流預混火焰受上游速度擾動下的非線性響應特性。為了驗證數值仿真結果的可信性,將獲得的結果與文獻實驗結果[18]比較,兩者吻合得較好。同時發現,改變火焰上游共振腔的長度對FDF的影響極小,這為未來長火焰燃燒室的穩定性和極限環的分析提供了新的視角。

1.3 理論研究

實驗方法和數值模擬方法對FTF/FDF的特征有深入且全面的認識,且獲得的結果也翔實可靠。但必須指出的是,實驗和數值模擬方法仍然存在一定的局限性。相比于解析推導方法,其經濟和時間成本無法忽略。因此,對現有FTF/FDF問題進行適當簡化,使用解析推導的方法捕捉火焰對于上游輸入擾動響應的基本特征具有較廣的適用范圍。

目前通用的描述火焰響應的方法為基于火焰面來描述燃燒熱釋放率,又稱為解析推導方法,其本質是使用G方程捕捉火焰前鋒面的動態演化。

(2)

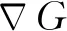
(3)

式中:YF為燃料的質量分數;A為火焰面積;ρ為火焰上游工質的密度。針對層流或弱湍流預混火焰,存在以下近似關系:

(4)

因此,可以通過無量綱火焰面積波動獲得無量綱熱釋放率脈動:

(5)

進而可以計算FTF和FDF。

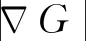
Lieuwen[21]使用G方程捕捉受到來流擾動且以一定火焰傳播速度傳播的層流預混火焰前鋒面,并詳細探討了火焰的非線性響應規律。結果表明,解析結果得到的火焰非線性響應特性與實驗結果[22]吻合較好。由于非線性現象存在,隨著上游來流擾動幅值的增加,FDF的幅值低于FTF的幅值的特性明顯加強,而FDF的相位對來流擾動幅值的變化并不敏感。火焰響應的非線性效應和Strouhal數St(St等于上游擾動頻率和管出口直徑的乘積并除以層流火焰燃燒速度)、穩態火焰高度、寬度比值β,以及火焰的類型(錐形火焰和V形火焰)密切相關。在火焰線性響應的特殊情形下,可以將St和β這兩個參數整合為參數St2=St(1+β2)/β2。此外,同樣發現,V形火焰的非線性響應特性比錐形火焰更明顯。

在G方程中考慮湍流的思路有兩種。第一種是在式(2)中的火焰傳播速度項S里考慮湍流,即認為火焰以湍流燃燒速度ST向前推進,這種方法由Lipatnikov等[23]首次提出,被稱為無強迫火焰模型(UFSM)。值得注意的是,在利用這種方法構建湍流預混火焰響應模型之前,需要通過其他方法來量化ST。Lipatnikov等[24]量化了湍流傳播速度,表達式如下:

(6)

式中:S0為完全發展的湍流傳播速度;t為湍流長度尺度;u′為湍流速度尺度;t′為火焰發展時間。將式(6)代入到式(2)中即可量化湍流火焰受上游聲波擾動的動態響應特性。但需要指出的是,在這項研究工作中忽略了火焰垂直于自身向前發展而引入的非線性源項因此其得到的FTF幅值在低擾動頻率下不夠準確。

Palies等[25]使用類似的方法計算了旋流湍流預混火焰的傳播速度并在此基礎上結合G方程推導了FDF。他們首先給出了火焰的傳播速度:

(7)

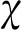
(8)

式中:i表示虛數單位;相位差φ通過實驗[12]獲得。

第二種考慮湍流的思路是在式(2)的火焰上游速度描述項u里引入湍流波動,這種方法最開始由Preetham等[26]使用,他們在火焰上游中考慮湍流波動并使用水平集方法來獲取錐形湍流預混火焰受上游來流擾動的響應規律。Hemchandra等[27]借鑒這種方法構建了V形湍流預混火焰受上游來流擾動的非線性解析模型。他們使用高斯密度分布函數來量化湍流波動,并根據泰勒假設將湍流波動整合到上游速度中,以此來量化受湍流影響的V形火焰動態特性。

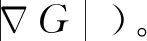
使用簡化模型來量化上述擾動傳播速度和擾動頻率的關系并將其耦合進G方程的模型中十分必要,火焰褶皺會通過對流特性反饋影響火焰周圍的速度場。Birbaud等[29]基于該思路,提出了基于火焰上游速度勢的模型來定量分析火焰上游擾動傳播速度和頻率之間的關系,其結果所呈現出的空間特性與實驗吻合較好。

通過對現有使用解析推導得到的FTF/FDF結果的回顧可以發現,FTF/FDF的解析方法在捕捉層流預混火焰的動態響應規律、非線性響應特性以及湍流預混火焰基本響應特性方面都具有一定的可行性。但目前大部分FTF/FDF的解析推導工作仍然局限于模型簡單的單一輸入。對于火箭發動機、航空發動機和燃氣輪機中被廣泛觀察到的多模態耦合影響下的火焰動態響應特性、火焰拉伸對真實發動機中的火焰模型的影響的研究尚少。因此,借鑒現有FTF/FDF解析推導方法的思想,并將其推廣并應用至多模態、考慮曲率影響下火焰響應性規律的研究中具有重要意義。

2 橫向和縱向擾動下火焰響應特性研究

在火箭發動機以及航空發動機、地面燃氣輪機的環形燃燒室中廣泛觀察到橫向流動擾動和縱向流動擾動同時存在的現象。已有研究表明,火焰上游橫向擾動的存在會顯著影響火焰對來流擾動響應的整體特性。下文主要討論使用解析方法來量化橫縱向擾動耦合下的火焰動態響應特性。

Palies等[25]構建了受來流擾動影響下的旋流預混湍流火焰線性響應解析模型,并將時均的湍流波動使用UFSM的方法代入線性化的G方程中來捕捉湍流火焰的褶皺前鋒面。此模型首次同時考慮了軸向和橫向擾動對旋流火焰動態響應特性的影響。結果表明,旋流火焰的動態響應特性可以參考受軸向擾動下錐形預混火焰的FTF進行分析。將兩種工況下得到的解析結果和實驗結果[12]分別進行比較,結果定量吻合較好。這意味著,使用解析推導方法量化存在多向擾動影響下的湍流預混火焰動態響應特性是可行的。

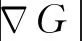
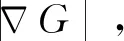
進一步,針對具有橫向和縱向速度擾動和平均流的二維槽道層流預混火焰建立了完全/部分非線性FDF和線性FTF,明確了單向擾動自非線性和雙向擾動耦合的互非線性對火焰熱釋放率響應的影響[34]。基于G方程結合漸進分析方法得到了火焰前鋒面軌跡。提出了一種基于K(表征縱向平均速度和擾動傳播速度的比值)和無量綱角頻率St(角頻率與燃燒器半徑的乘積除以縱向平均速度)的分析模型,量化了特定頻率St對應的擾動傳播速度。如圖2所示,得到了不同雙向擾動幅值下的線性和完全/部分非線性熱釋放率脈動響應的整體差異。

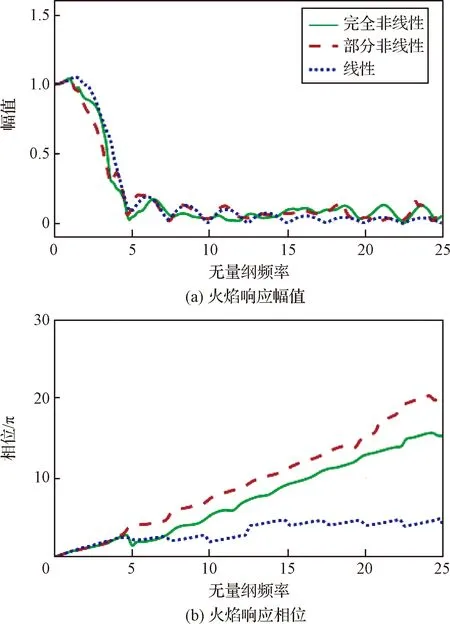
圖2 雙向擾動輸入下火焰的線性、部分非線性和完全非線性響應結果隨無量綱頻率的變化關系[34]Fig.2 The linear, partially nonlinear and fully nonlinear response results of the flame under bidirectional perturbation input as a function of non-dimensional frequency[34]

研究結果表明,當縱向擾動幅值變大時,火焰響應的非線性特征十分明顯,此時線性和非線性響應的幅值差異明顯(部分非線性和完全非線性的結果差異同樣明顯)。通過對比FDF和FTF的相位可以發現,橫向擾動對相位的影響不明顯,特別是此時部分非線性結果和線性結果的相位幾乎沒有差別。而縱向擾動幅值的增加會在自非線性項中抑制擾動的傳播(和線性結果相比,相位差增加),但在互非線性項中增強擾動的傳播(和部分非線性結果相比,相位差降低)。總之,當擾動頻率較高或擾動幅值較大時,自非線性項和互非線性項在火焰對雙向擾動響應中無法忽略。

為修正火焰以恒定傳播速度垂直于火焰鋒面向反應物發展這一假設產生的誤差,課題組期望改進經典的UFSM方法,以克服其對G方程進行一階線性化忽略火焰垂直于自身向前發展的非線性源項而引入的缺陷,量化了二維槽道非對稱預混火焰前沿動態對特定雙向擾動的非線性響應,將該方法命名為雙向非線性無強迫火焰速度模型(2W-NUFSM)[35]。具體而言,此方法基于無量綱橫向擾動幅值和縱向擾動幅值的兩參數二階攝動方法描述火焰前沿動態軌跡,并將湍流效應通過火焰前沿推進速度和穩態火焰鋒面兩個參數考慮至模型中。為了使用2W-NUFSM量化諧波擾動耦合湍流波動對火焰前沿動態的影響,需要提前確定火焰前沿傳播速度和穩態火焰鋒面對湍流波動的響應特性。此外,改進了Hemchandra等[27]的方法,基于湍流波動幅值將火焰前沿方程漸進展開至二階精度,并求解了湍流波動下的火焰傳播速度和集總平均火焰鋒面,分析了湍流波動對FDF影響的途徑并進一步確定了諧波擾動和湍流波動耦合作用對火焰響應的影響規律。

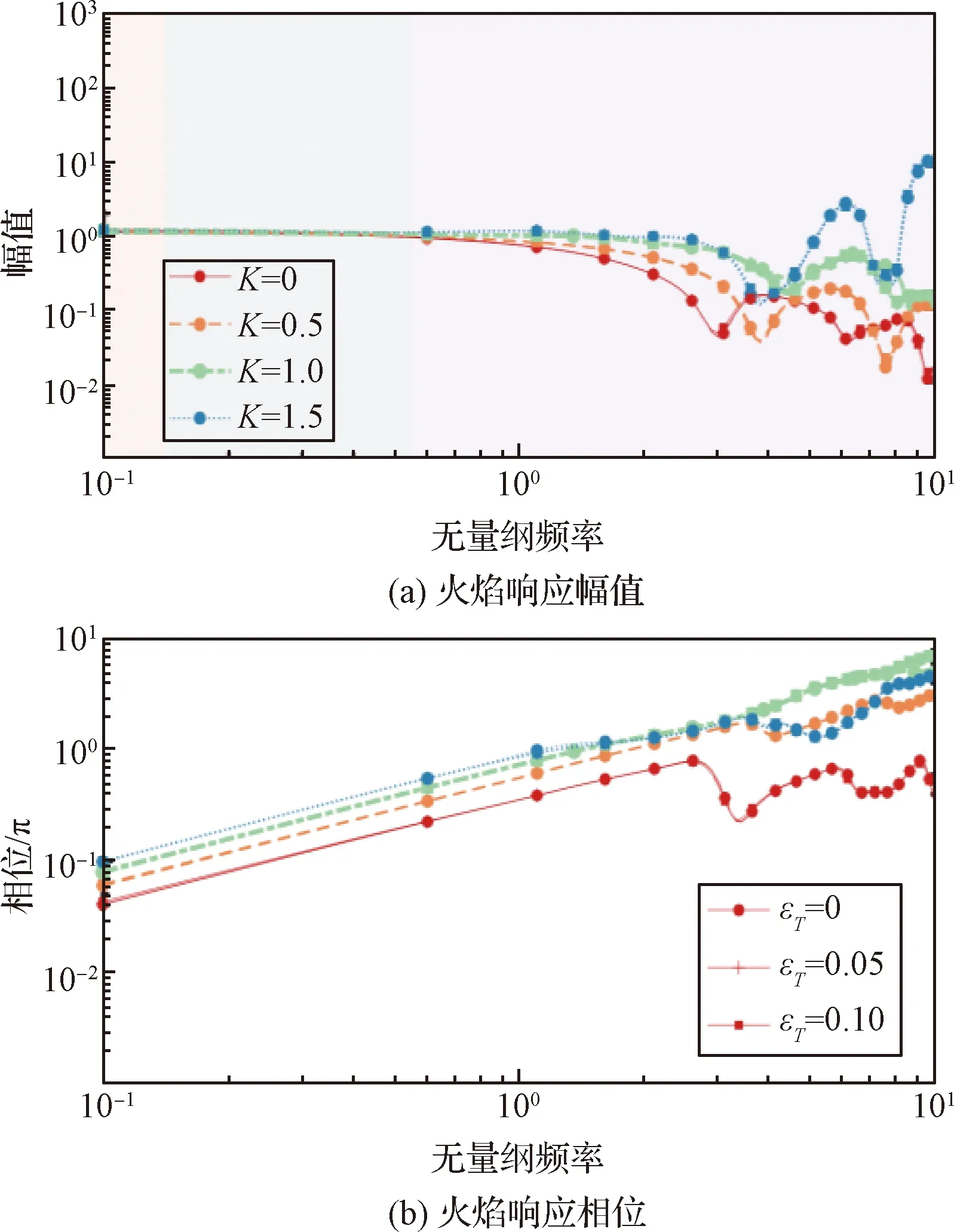
圖3 火焰響應幅值和相位隨著無量綱頻率以及不同K和εT變化而變化[35]Fig.3 The flame response amplitude and phase vary with non-dimensional frequency as well as with different K and εT variations[35]

當諧波擾動頻率較低時,湍流直接通過湍流波動幅值εT影響FDF的幅值。當諧波擾動頻率在中頻或者高頻時,湍流通過K(與擾動傳播速度uc負相關)影響FDF幅值。當諧波擾動頻率較低時,湍流對FDF相位的影響主要由K控制,但當擾動頻率較大時,上述關系將被擾動頻率St影響。由于存在火焰運動學恢復效應,尺度越小的褶皺(對應于越小的uc即越大的K)越容易被運動收縮抹平,進而導致火焰動態響應幅值消散。當擾動頻率增加,諧波擾動的波長減小。當諧波擾動波長與湍流褶皺的尺度相同時,火焰運動學由諧波擾動和湍流波動同時控制。由于小尺度褶皺誘發產生大幅值褶皺,因此火焰運動學收縮對火焰前沿褶皺的消除隨著K的增加而增加,與K對FDF幅值復雜的影響不同,其對相位的影響更有規律且較輕微。

3 縱向雙(多)頻率擾動下火焰響應特性研究

多模態擾動耦合振蕩影響火焰的現象廣泛存在于發動機的燃燒室中,火焰與聲波的耦合會激發出多種頻率下的響應。多頻擾動并非簡單的單頻線形疊加,而是具有新模態生成、模態抑制、模態強化等非線性作用。因此目前廣泛研究的單一頻率下的擾動有很大的局限性,雙頻擾動的研究更加貼合發動機的實際工作環境。

Balachandran等[36]對V形層流預混火焰輸入兩個不同頻率的諧波擾動,來探究火焰的非線性響應特征。結果顯示:由于額外引入的諧波或者亞諧波擾動,渦的形成和脫落過程明顯受到影響。隨著高頻分量(320 Hz)的幅值增加,在160 Hz處的火焰傳遞函數收縮明顯。此結果表明,可以通過對火焰引入特定頻率處的額外擾動來抑制潛在的熱聲不穩定性。Lamraoui等[37]實驗研究了具有兩個非諧波相關不穩定模態(180 Hz和280 Hz)的湍流旋流預混燃燒室的熱聲不穩定性。與先前典型的單不穩定模態主導的現象相比,額外不穩定模態的引入不僅深刻改變了火焰的動態響應特性,同時也影響了對應的熱聲不穩定性,其中低頻模態影響了縱向的振蕩,而高頻模態導致了徑向的流動褶皺。

Haeringer等[38]分析了高次諧波對FDF的影響,引入了新的FDF來量化高階諧波對應的熱釋放率與相對應頻率的速度擾動的比值,以此來擴充原有的FDF,并將其稱之為擴展火焰描述函數(extend-FDF);詳細介紹了如何確定extend-FDF,并將其用來預測極限環振蕩。結果表明,extend-FDF獲得的結果和全可壓縮數值仿真模型的結果吻合的較好。這意味著當高次諧波對熱聲極限環振蕩起決定性作用時可以使用extend-FDF來描述實際火焰響應。

Orchini等[39]將FDF耦合到燃燒室的線性聲學網絡中,通過諧波平衡方法來預測諧波熱聲耦合振蕩的幅值和穩定性。然而在某些特定工況下燃燒室內會出現多個非相關的頻率進而產生非周期振蕩。他們對這一現象進行簡化,認為只有兩個基礎頻率影響火焰響應,此時整個聲學系統以準周期的形式發生振蕩。以此將FDF推廣來確定火焰對同時存在兩個頻率不同,幅值不同和相位不同的來流擾動的動態響應特性,并將其稱為雙輸入火焰描述函數(FDIDF)。使用G方程針對層流預混錐形火焰構建了非靜態DFIDF,并將其與熱聲網絡進行耦合,以此來預測諧波熱聲耦合振蕩的幅值和穩定性。通過與經典FDF比較,發現DFIDF具有預測Neimark-Sacke分叉和非穩態極限環狀態下系統的振蕩頻率的能力。因此,在存在多頻擾動耦合振蕩的燃燒室中,考慮多頻擾動耦合對火焰動態響應的影響是關鍵且必須的。

本課題組為了明確額外擾動對火焰受原有擾動影響的響應特性的改變,給定了兩個頻率、幅值、相位都相互獨立的諧波擾動(分別命名為原有擾動和額外擾動),并將其輸入火焰來探究它們在火焰響應中的非線性耦合機制。火焰響應的非線性結果通過G方程結合低階漸進分析(擴展至關于無量綱擾動幅值的三階)和數值方法獲得。由于火焰垂直于自身向反應物一側發展,基于漸進分析可知,原始擾動和額外擾動在火焰響應中產生了三階非線性耦合并改變了火焰在原始擾動頻率處響應。其典型結果如圖4所示,可以發現,火焰在原始擾動頻率處的響應主要由線性項構成,而非線性項在此基礎上對其幅值和相位進行修正。隨著火焰向下游發展,火焰響應的幅值衰減明顯,相位的階躍現象也得到抑制。

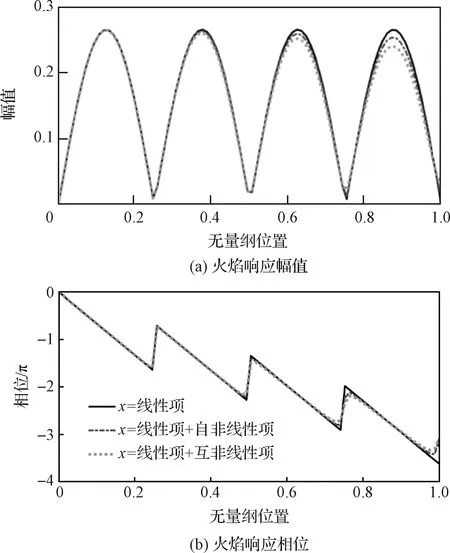
圖4 原始擾動頻率處火焰空間響應對原始和額外擾動非線性的依賴[40]Fig.4 Dependence of the spatial response of the flame at the original perturbation frequency on the original and additional perturbation nonlinearities[40]

4 火焰曲率效應對FTF/FDF的影響作用

當火焰尺寸較小時,由于張力和熱擴散的影響,火焰傳播速度受到流動梯度的影響,導致每個位置的火焰拉伸不同,進而影響了整體放熱速率。因此,錐形火焰鋒面在一定頻率范圍內會變成半球形,這進一步凸顯了考慮火焰曲率效應的必要性。

在G方程模型中,火焰曲率拉伸速率對火焰速度的影響通常由馬克斯坦長度L表示,一般結合火焰厚度將其表示成無量綱形式——馬克斯坦數L/δ,此參數主要反映不同的燃料種類及當量比。常用的幾種碳氫氧燃料的對應關系已通過實驗進行研究[41],其中氫氣和甲烷的馬克斯坦數隨著當量比增大而增大,而其它絕大多數燃料,兩者呈負相關。

火焰曲率拉伸通過影響火焰燃燒速度,進而影響火焰熱釋放率,因此在理論上對G方程中的火焰傳播速度SL進行修正[42]:

(9)

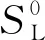
Preetham等[43]的研究結果表明,火焰曲率拉伸會影響燃燒速度沿火焰褶皺鋒面的傳播情況,整體線性火焰響應取決于馬克斯坦長度和無量綱Strouhal數。當LSt～O(1)時,火焰曲率拉伸效應會變得明顯,并導致火焰鋒面褶皺減小,此現象表明組成LSt的馬克斯坦長度、火焰高徑比、平均流速和特定頻率是決定火焰曲率拉伸效應是否顯著的關鍵參數。Wang等[44]進一步的理論研究表明,當擾動頻率在一定范圍時,火焰曲率拉伸效應在火焰傳遞函數中發揮著重要作用。具體來說,低于某一擾動頻率時,火焰曲率拉伸效應很小,火焰響應與未考慮拉伸時基本一致;而高于此頻率且在一定范圍時,火焰面積受火焰曲率拉伸的影響強烈,進而影響火焰傳遞函數。

從實驗結果來看,火焰曲率拉伸的作用同樣非常明顯,其中小尺寸火焰受影響較大。Kornilov等[45]的研究結果表明,多孔火焰的孔徑和孔隙率是影響火焰傳遞函數和火焰描述函數的主要參數,主要影響在于會使幅值在特定頻率范圍內超過1。此外,當孔隙率不變時,隨著孔徑減小,火焰傳遞函數幅值隨頻率先增大而后降低的過程變得緩慢,相位降低;當孔徑不變時,孔隙率越大,相位越大。上述現象可通過不同尺寸火焰的形狀受到拉伸的影響程度不同來解釋,此研究為多孔火焰燃燒器噴嘴的設計提供了參考。

Gaudron等[46]引入了無量綱頻率,將不同尺寸的火焰進行相似性類比。當火焰尺寸較大時,相似尺寸火焰的傳遞函數表現出相似性,無量綱處理后基本重合;而當火焰較小時,由于火焰厚度相比火焰半徑來說不可忽略,需要額外的參數來完整描述FTF。此外,結果表明,特定的路易斯數和火焰溫度會導致小火焰傳遞函數在低頻時增益值超過1,稱為增益過沖。由圖5可知,在低頻速度擾動下,當噴嘴尺寸減小或火焰溫度降低時,傳遞函數峰值對應的無量綱頻率較低。基于此實驗結果完善了考慮火焰底部相鄰火焰相互作用和不穩定傳熱傳質的模型,相較于基于平面火焰的模型,此模型更準確。

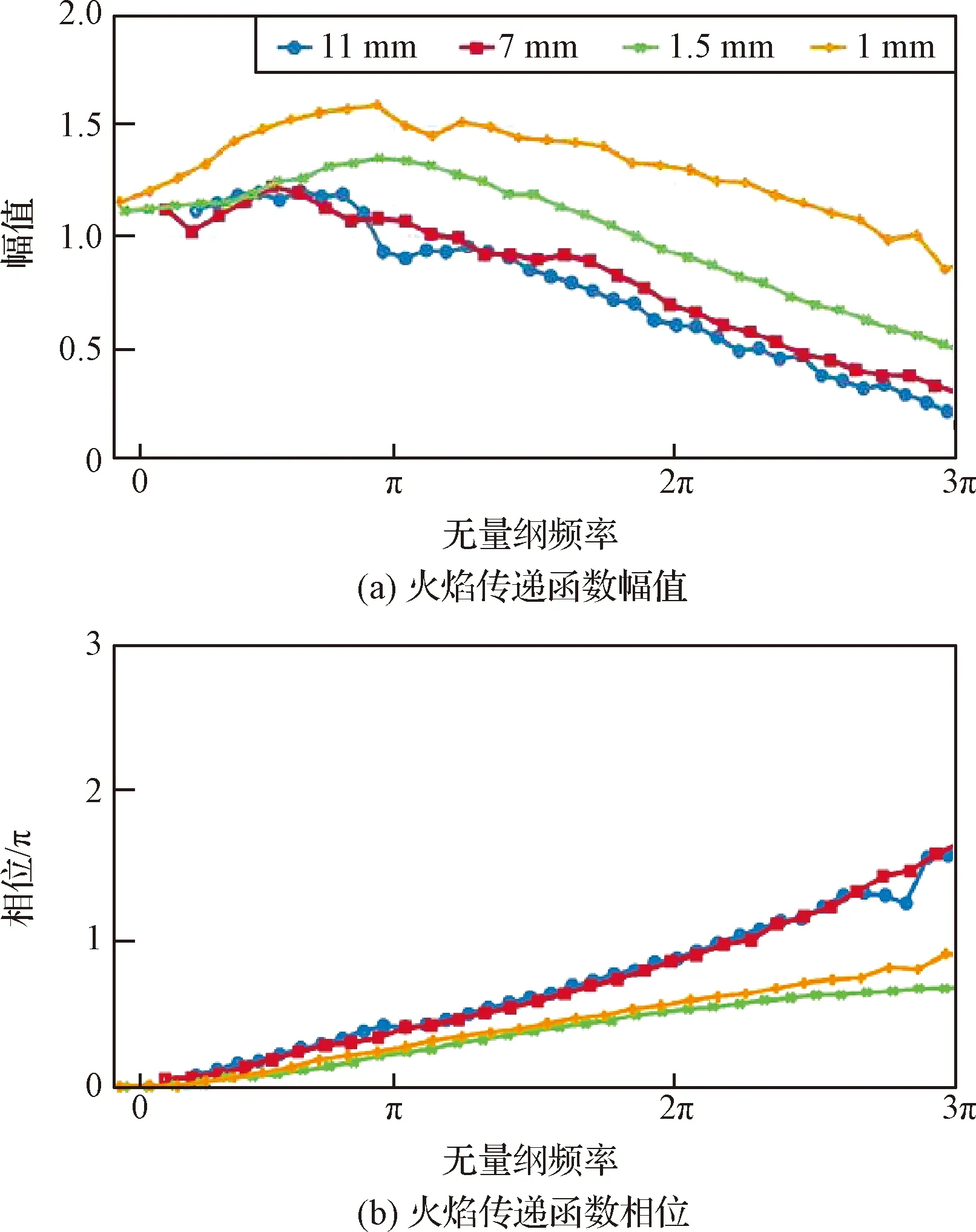
圖5 不同噴嘴半徑的火焰傳遞函數[46]Fig.5 Flame transfer function for different nozzle radius[46]

Kedia等[47]通過數值仿真方法研究了火焰根部的錨定情況對火焰曲率拉伸的影響。結果表明,火焰根部會錨定在流動速度和火焰位移速度相同的地點,該位置由熱損失和火焰拉伸對火焰位移速度的綜合影響決定。隨著反應物入口速度的增加,該位置的火焰位移速度呈非單調變化,變化主要表現為:回流區逐漸擴大,火焰向下游移動,燃燒器的熱損失減少,火焰加長,位移速度增加。而入口速度的進一步提高會導致吹熄,吹熄期間的火焰速度由增長的再循環區和冷卻燃燒器板之間的反饋決定。

Cuquel等[48]對火焰根部和燃燒器噴嘴之間的不穩定傳熱響應進行了理論研究,并稱之為火焰基振蕩,修正了錨點運動時的火焰傳遞函數,并將修正前后的結果進行了比較。結果表明,傳遞函數相位出現非線性行為,速度擾動導致相位滯后隨頻率增加,而火焰基振蕩導致相位滯后在高頻下飽和,兩者之間存在競爭。此外,擾動幅值的增加會導致火焰傳遞函數在較低頻率下的相位滯后,提前飽和。該分析證明了火焰根部振蕩在控制傳遞函數相位滯后飽和度方面的重要作用。

5 火焰傳遞函數對固有熱聲不穩定模態的影響

在熱聲不穩定的研究中,FTF/FDF的主要應用方式為代入到諸如線性歐拉方程、亥姆霍茲方程和低階聲學網絡模型等求解器的熱源項中來對流動擾動和熱釋放率擾動之間的相互作用進行說明,進而實現對熱聲不穩定性的預測。近些年來有學者將系統熱聲振蕩模態基于燃燒室聲學特征和燃燒特性進行了劃分[49]。研究表明,即使在無聲學反射的邊界條件下,依然存在熱聲振蕩現象,并將這種熱聲振蕩現象命名為固有熱聲不穩定性(ITA)。

在早期研究中已經發現了在熱聲系統中存在很多難以解釋的振蕩模態,Dowling等[50]通過構建薄環形LPP燃燒器熱聲系統振蕩的線性模型,結合簡單的火焰模型對燃燒器內的熱聲振蕩模態進行了預測,發現了許多無法解釋的與聲學特征值無關的熱聲振蕩模態。但是這些問題通常被歸結于火焰模型過于簡單和線性模型不夠完善,并未引起注意。在近些年的研究中發現,上述問題可以通過ITA模態進行解釋,即實驗中所測試到的熱聲振蕩模態存在著兩種主導因素[49]:一種是燃燒室聲學特征主導的模態,被稱為聲學主導模態;另一種是由火焰響應主導的模態,這類模態被稱為ITA主導模態。研究表明,在逐步去除燃燒室火焰響應和聲學特征(邊界聲學反射)時,熱聲模態會分別退化至兩種基本模態:純聲學模態(不存在火焰響應時的熱聲振蕩模態)和ITA模態(不存在邊界聲學反射的熱聲振蕩模態)。在多數情況下,燃燒室中的熱聲模態受到上述兩種模態共同影響,且由其中一種模態主導。

熱聲振蕩系統中的ITA模態是與火焰響應緊密相關的一種模態。對于這種ITA模態與火焰響應之間的關系,目前學界的基本認識為,在火焰處由于火焰耦合作用構成了一個內在的反饋環。如圖6所示,其基本的反饋過程為:火焰受到上游一點的速度擾動后產生熱釋放率波動,熱釋放率波動作為聲源會產生聲波,聲波向上游和下游傳播,其中向上游傳播的聲波會在燃燒室入口、鈍體等燃燒室上游結構邊緣處產生渦脫落并造成流動擾動,隨后流動擾動進一步向下游傳播引發熱釋放率擾動,構成反饋環[51]。從上述過程可以看出,ITA模態與火焰本身性質密切相關,且與燃燒室內的聲學特征無關,而與熱釋放率對于速度擾動的響應(FTF/FDF)有著相當緊密的聯系。

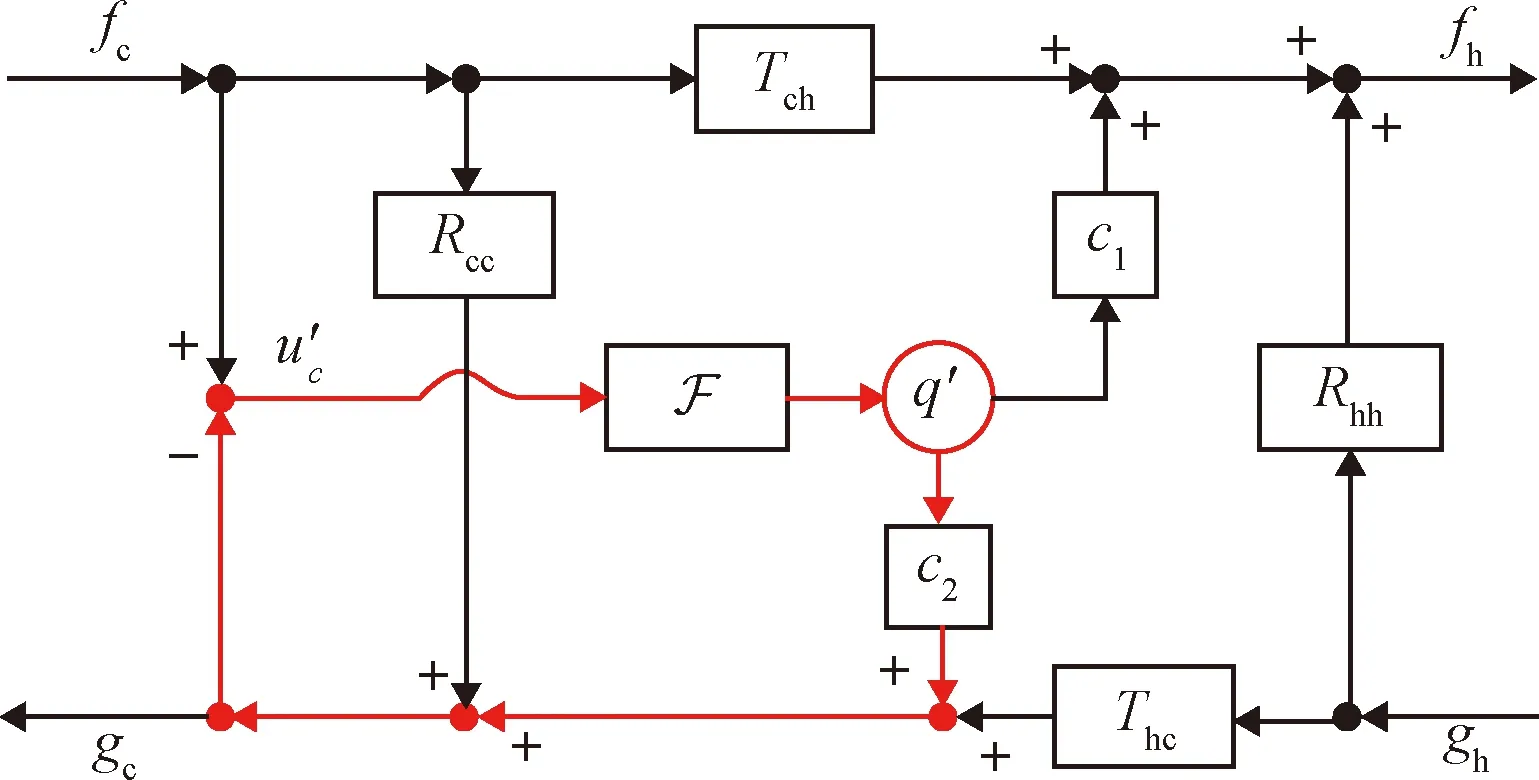
圖6 ITA模態反饋環[52]Fig.6 ITA mode feedback loop[52]

在上文中,深入探討了不同火焰對于不同方向、不同頻率及不同幅值的速度擾動的影響作用。在下文中,將對火焰響應(FTF/FDF)和燃燒室中ITA模態之間的關系及進行討論。討論主要分為兩個部分,第一部分為火焰傳遞函數和ITA模態之間相互作用的理論研究;第二部分主要討論基于實驗和仿真研究FTF/FDF與ITA模態之間的關系。

值得注意的是,下文主要是討論FTF/FDF和ITA模態之間的關系,不同學者對于ITA模態的求解方式不同,目前主流的為:散射矩陣極點、低階聲學網絡模型、開環傳遞函數、相量圖、穩定性邊界、亥姆霍茲方程和仿真求解等。以下討論不會著重關注ITA模態的求解方式。

5.1 理論研究

在近年來對ITA模態的研究中,Hoeijmakers等[53]和Emmert等[54]的工作具有開創意義,通過結合n-τ構建低階聲學網絡模型并對其進行簡化,得到散射矩陣,隨后通過散射矩陣對燃燒室的熱聲振蕩進行討論,發現了火焰內部存在ITA反饋環,進而提出ITA模態,其中n-τ模型如下所示:

F=ne-iωτ

(10)

式中:n為耦合強度;τ為相位延遲;ω=2πf+iσ,其中σ表示增長率,f表示頻率。此外也通過散射矩陣的極點來說明了ITA模態的振蕩頻率及穩定性邊界:振蕩頻率由n-τ模型中的相位延遲τ確定(又被稱為-π準則,即ITA模態頻率為1/τ);穩定性邊界由燃燒室參數和n-τ模型中的耦合強度n確定。結果表明,隨著邊界反射系數的逐漸減小至0,燃燒室中的一些振蕩模態逐步轉向ITA模態。此外,通過仿真和實驗方法驗證了上述結果[55]。這一研究工作將燃燒室中的熱聲振蕩模態進行了分類,并給出了完整的預測方法。

Hosseini等[56]和Sogaro等[57]通過將n-τ模型應用于一維Rijke管模型并通過低階聲學網絡模型對其ITA模態進行預測,詳細分析了燃燒室內各種參數如邊界反射系數,耦合強度n、相位延遲τ和火焰處面積擴張比對ITA模態和純聲學模態之間的影響作用。結果表明,部分ITA模態和純聲學模態之間存在著周期性相互轉換的關系。此外,通過偽光譜法分析發現,能量增大對純聲學模態和ITA模態之間的相互作用至關重要,而火焰是能量增大的主要來源。

Mensah等[58]、Buschmann等[59]、Silva等[60]、Orchini等[61]和Ghani等[62]在一維縱向和環形燃燒室中應用n-τ模型研究ITA模態時,發現隨著火焰傳遞函數中n和τ改變,系統中的熱聲振蕩模態分布出現明顯的奇異點,且這一現象廣泛存在。如圖7所示,在奇異點附近,ITA模態具有非常大的靈敏度并表現出強烈的模態轉向,此結果在三維軸向和環形燃燒室中進行了數值驗證。上述研究中使用的研究方法為低階聲學網絡模型或亥姆霍茲方程結合n-τ模型進行求解。上述結果說明燃燒室中的純聲學模態和ITA模態之間的相互作用受火焰響應影響極大,而對于真實的燃燒室系統的火焰響應,這種作用會更加復雜。

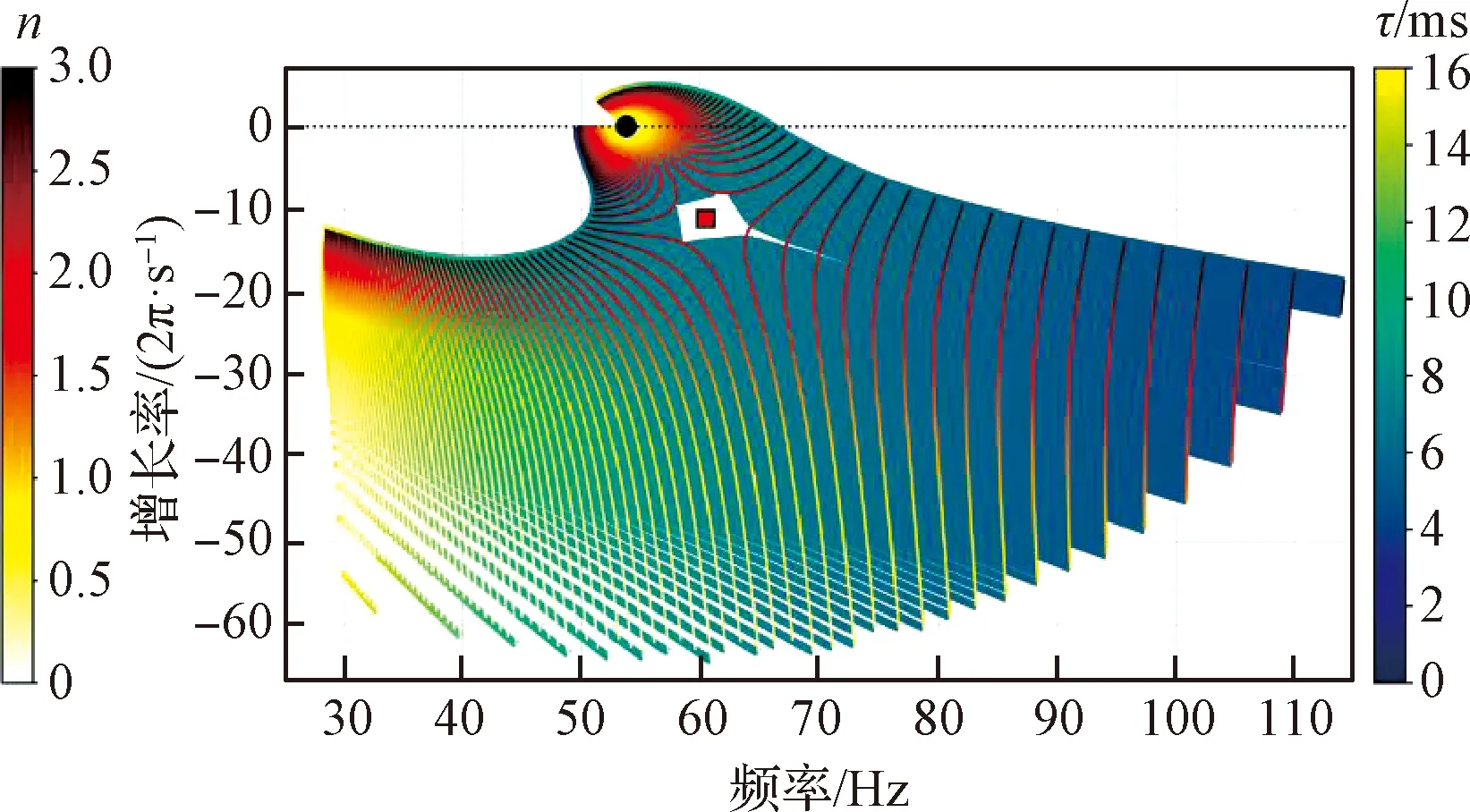
圖7 特征值跡線中奇異點的位置(n和τ表示n-τ模型參數)[61]Fig.7 The location of exceptional points in the eigenvalue trajectories (n and τ represent n-τ model parameters respectively)[61]

Buschmann等[57]通過結合n-τ模型和亥姆霍茲方程的方法研究了薄壁環形燃燒室中的ITA模態并進行了仿真驗證。結果表明,環形燃燒室中確實存在ITA模態,且ITA模態的分布也符合-π準則,此外模態分布具有成簇的特殊行為,即頻率相近的幾種模態,說明環形燃燒室中的ITA模態存在聚類現象。

本課題組也對一維Rijke管模型和環形燃燒室模型中的ITA模態進行了理論研究[63]。主要是通過應用n-τ模型,結合組內研究基礎[64-65],并參考了Li等[66]的研究方法,構建了考慮平均流、渦波和熵波的更完善低階聲學網絡模型并對ITA模態進行了研究。以往的研究忽略了平均流的影響作用[57],但是研究結果表明[63],平均流對ITA模態的增長率影響很大,而對ITA模態的頻率影響不大,馬赫數的增加使得所有ITA模式都更加不穩定,且對不同模態的穩定性影響不同。此外研究發現,當考慮平均流時,在環形燃燒室中發現了一種新的不符合-π準則的ITA模態,這一模態的存在很可能與環形燃燒室中的渦波和熵波有關。

5.2 實驗和仿真研究

相較于簡化的n-τ模型及基于其修正的火焰傳遞函數,基于仿真和實驗數據提取的FTF/FDF更加完善且具有代表性。本節的主要研究思路為通過仿真和實驗數據獲取FTF/FDF,隨后將其代入到低階聲學網絡模型或者亥姆霍茲方程中進行ITA模態的求解,將求解得到的ITA模態與仿真或實驗中觀測到的熱聲振蕩模態或ITA模態進行比對,從而進行分析。

早期對于ITA模態的仿真和實驗工作主要是驗證ITA模態的真實存在。Emmert等[54]和Bomberg等[67]通過系統識別的方法從BRS旋流燃燒器、ECP層流預混燃燒器、TD1湍流預混燃燒器實驗數據和大渦模擬仿真數據中提取火焰傳遞函數。將火焰傳遞函數結果代入到由色散矩陣極點獲得的開環傳遞函數中,并基于尼奎斯特判據對ITA模態的位置和穩定性進行預測,最后與實驗和仿真觀測結果進行對照。結果表明,理論預測結果和觀測結果一致,說明ITA模態真實存在,且熱聲系統中的振蕩可以由ITA模態引起。此外,Emmert等[54]還從聲功率平衡的角度分析了火焰固有反饋回路與熱聲系統不穩定潛力的關系。

Courtine等[51]通過直接數值模擬的方法研究了預混本生燈火焰燃燒系統的ITA模態。通過對多種工況的對比分析,如圖8所示,詳細探究了ITA模態下一個振蕩周期內的火焰面變化,基于火焰響應提出了ITA模態反饋環的理論解釋,即模態轉換和運動學過度恢復。值得注意的是,模態轉換發生在燃燒室入口拐角處,受上游速度擾動的影響,此處會產生渦,而火焰的錨點也在此處,渦和錨點的相互作用引發了模態轉換。在振蕩周期的初始階段,火焰錨點會被渦推開,火焰會被持續拉長,隨后發生運動學過度恢復。由于此時火焰遠離其平衡位置,且入口速度也是最小狀態,所以火焰會快速收縮,而火焰的強烈收縮導致了負的擴張和聲壓,這反過來又誘發了火焰上游的速度激增。而入口速度的增加會再次誘發燃燒室入口拐角處的模態轉換,并產生了一對新的渦,從而構成新的循環。可以看出,上述ITA模態的所有振蕩過程和火焰響應,即FTF/FDF有著至關重要的直接聯系,也正因此,對于火焰動力學的研究對ITA模態和熱聲振蕩模態的研究具有重大意義。

ITA模態的實際實驗測量需要消除聲學的邊界反射,Hoeijmakers等[68-69]提出了一種通過安裝喇叭來消除邊界聲學反射的方法,并在邊界存在大量聲學損失的條件下對層流預混本生燈火焰的熱聲振蕩進行了實驗研究。此外,他們通過實驗測量得到火焰傳遞函數,并將其代入低階聲學網絡模型中進行ITA模態的預測。結果表明,即使在邊界處存在大量聲學損失的情況下,熱聲系統也會表現出不穩定性,這一實驗結果證實了ITA模態的存在并為早期ITA模態的理論提供了實驗依據。

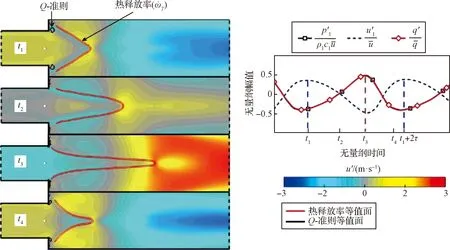
圖8 固有熱聲不穩定振蕩模態下的一個完整振蕩周期(其中黑圈表示渦)[51]Fig.8 One complete period of oscillation in the intrinsic thermoacoustic instability oscillation mode, where the black circle indicates the vortex[51]

Silva等[70-71]和Albayrak等[52]對層流預混本生燈火焰和BRS旋流燃燒器分別進行直接數值模擬和實驗研究。研究結果表明,對于上述的兩種燃燒室,ITA模態均真實存在,且不受燃燒室聲學特性的影響。值得注意的是,在對BRS旋流燃燒器進行的實驗研究中,低階聲學網絡結合系統識別得到的FTF預測的ITA模態結果與真實的實驗結果一致性很好。從實驗結果中還發現在這個特定的燃燒器中,ITA模態很普遍,并且不穩定的模態占比較多;ITA模態的頻率隨著體積流速和旋流器位置的變化而明顯改變,但對燃燒室長度的變化不敏感。上述實驗結果和規律對ITA模態和火焰響應直接的相互作用提供了堅實依據。

Murugesan等[72]和Vishwakarma等[73]對工業燃氣輪機上實際應用的大雷諾數(Re>13000)湍流部分預混旋流燃燒器中的ITA模態進行了實驗研究,其中燃料為體積占比40% C3H8和60% C4H10組合的液化石油氣,空氣由大型壓縮機提供。結果表明,低階聲學網絡預測的頻率與實驗觀察到的振蕩主頻率非常一致。此外,非穩態熱釋放熱率與燃料當量比波動之間的內在火焰聲學耦合作用對ITA模態有極大的影響,而這種耦合作用需要通過火焰描述函數進行詳細描述。

Ghani等[74]通過仿真方法研究了甲烷火焰中添加氫對ITA模態的影響作用。結果表明,氫燃料的加入增大了層流火焰速度,火焰整體長度明顯縮短。通過系統辨識的方法對FTF進行提取,隨著氫添加量的增多,火焰傳遞函數的幅值減小,相位增加。隨后將提取的FTF應用于-π準則和穩定性邊界來預測ITA模態,預測結果和燃燒室內真實壓力振蕩頻率較為一致,且更大的氫的添加量增大了ITA模態頻率,顯著增強了同一頻率下ITA模態的穩定性。上述結果說明可通過添加氫氣來縮短火焰高度,改變火焰響應特性,進而實現ITA模態的控制。這一結果與Tang等[75]對“馬克斯坦長度隨著氫分數的增加而增加,表明氫的加入穩定了火焰”的論述一致,說明穩定的火焰有利于ITA模態的穩定。Cheng等[76]通過仿真方法探究了通過改變層流預混火焰中火焰穩定器的溫度來改變火焰傳遞函數,從而影響燃燒器中的ITA模態。結果表明鈍體溫度通過改變火焰附著區域可以顯著影響火焰響應,進而影響系統的ITA模態。上述結果證實了火焰響應主導了ITA模態,并對熱聲系統的振蕩模態施加影響。

Xu等[77]基于預混旋流燃燒器研究了當量比和聲襯對系統熱聲不穩定性的影響作用。實驗和理論研究結果表明在更高的當量比下,ITA模態比聲學模態更容易出現不穩定;此外,添加具有偏流的聲襯可有效抑制腔內純聲學模態主導的燃燒振蕩,但對ITA模態無效,且偏流馬赫數的增加會激發和增強不穩定的ITA模態;當量比顯著影響火焰傳遞函數,進而改變ITA模態。此外,結果中體現的聲襯等常用的熱聲振蕩抑制裝置的加入對熱聲系統中ITA模態主導的振蕩模態影響作用較為復雜,這也為熱聲不穩定的控制提供了一些指導和參考。

6 趨勢與展望

基于上述分析,對火焰受來流擾動的動態響應發展趨勢的概述如下:

1) 已有的理論研究主要集中于單模態擾動影響火焰的簡單情形。然而,多模態擾動耦合振蕩影響火焰現象廣泛存在于火箭、航空發動機和燃氣輪機的燃燒室中,如橫縱向擾動耦合振蕩以及單縱向多頻率擾動耦合振蕩等,其對應的燃燒不穩定也時有發生。現有文獻中對于多模態擾動耦合作用下火焰動態響應特性的研究較少且沒有對得到的結果進行詳細的說明和進一步的機理解釋。這顯然限制了對多模態擾動作用下火焰動態響應規律的深入理解。因此,將多模態擾動耦合作用下的火焰模型進行適當化簡,使用解析推導方法量化在它們的作用下火焰的動態響應特性,并深入探究其響應性規律,這對于理解和預測對應的燃燒不穩定具有重要意義。

2) 對火焰曲率的研究多局限于層流預混火焰受當量比影響而使得火焰形態發生變化,然而熱聲系統中流動擾動和熱釋放率擾動之間的耦合作用使得火焰曲率發生變化的機理非常復雜。火焰熱釋放率還會受到諸如壁面溫度和重力場環境等多種因素的影響,各種因素的耦合作用的影響同樣值得重視。此外,目前解析方法只能對較為簡單的層流預混火焰進行解析求解,難以實現對上述多種因素影響下的各種火焰進行描述。這些問題均需要更完善的理論模型和實驗研究,因此,實驗技術和測量儀器性能的進一步提升對火焰動態響應的研究也有著至關重要的意義。

3) 為了實現對熱聲不穩定的控制,需要對熱聲系統振蕩機理的深刻認識。對固有熱聲不穩定和火焰響應之間相互作用的機理研究對上述問題的解決起著決定性作用。但就目前的研究現狀來說,理論研究的局限性一方面在于火焰響應模型過于簡化,忽略了火焰的空間分布,以及缺少如旋流火焰、噴霧火焰和多火焰耦合的響應模型;另一方面在于固有熱聲不穩定的求解方法如低階聲學網絡模型和線性歐拉方程等不夠完善,難以實現對較復雜燃燒室內熱聲振蕩模態的預測。此外,實驗方面的局限性在于難以完全對常見的燃燒設備實現邊界聲學反射的消除,實驗測量儀器的精度也難以滿足燃燒室中的測量需求,也就難以實現對固有熱聲不穩定模態的精確測量,無法從實驗的角度分析火焰響應和固有熱聲不穩定模態之間的相互作用。上述的問題也是目前的研究趨勢和進一步的研究方向。

7 結束語

本文聚焦火箭發動機、航空發動機和燃氣輪機的燃燒室內廣泛觀察到多模態耦合振蕩產生熱聲不穩定,研究了火焰對多模態流動擾動的非線性響應特性,具體著眼于橫縱向擾動耦合和縱向雙頻擾動耦合作用下的火焰動態響應;此外考慮了火焰曲率拉伸對火焰傳遞函數的影響作用;最后對近年來出現的一種在燃燒室內與火焰傳遞函數和火焰描述函數緊密相關的固有熱聲不穩定模態進行了討論,著重分析了火焰響應對固有熱聲不穩定模態的影響作用。