按點分析，得心應手

文／晏南飛

平行四邊形和特殊的平行四邊形的解答題在中考中是較為常見的，涉及的知識點較多，綜合性較強，解題難度較大。那么，如何解答才能不失分？這就需要我們學會分解題目，踩點分析，規范書寫。下面就以2022 年內蒙古呼和浩特市的一道中考題為例說明。

下面是八年級教科書中的一道題：如圖1，四邊形ABCD是正方形，點E是邊BC的中點，∠AEF=90°，且EF交正方形外角的平分線CF于點F。求證：AE=EF。（提示：取AB的中點G，連接EG）

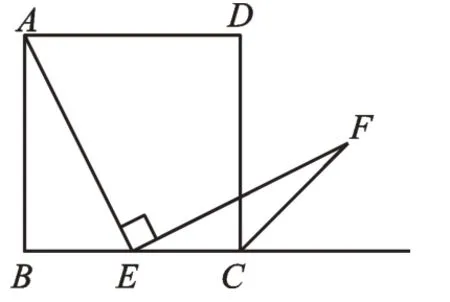
圖1

（1）請你思考題中“提示”，這樣添加輔助線的意圖是得到條件：___________。

（2）如圖2，若點E是BC邊上任意一點（不與B、C重合），其他條件不變。求證：AE=EF。

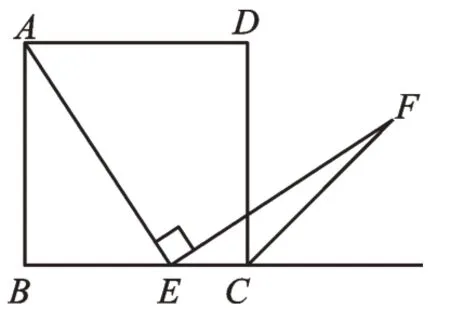
圖2

（3）在（2）的條件下，連接AC，過點E作EP⊥AC，垂足為P。設=K，當K為何值時，四邊形ECFP是平行四邊形，并給予證明。

解：（1）AG=CE。（2分）

（2）取AG=EC，連接EG，如圖3。（3分）

圖3

∵四邊形ABCD是正方形，

∴AB=BC，∠B=90°。

∵AG=EC，∴BG=BE。

∴△BGE是等腰直角三角形。

∴∠BGE=∠BEG=45°。

（3）當K=時，四邊形ECFP是平行四邊形。（7分）

取AG=EC，連接EG，如圖4。

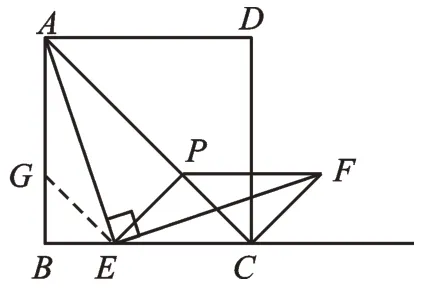
圖4

由（2）得△CEF≌△GAE，∴CF=EG。設BC=x，則BE=Kx，

∴GE=Kx，EC=（1-K）x。（8分）

∵EP⊥AC，

∴△PEC是等腰直角三角形。

∴∠PEC=45°。

∴∠PEC+∠ECF=180°，PE=（1-K）x。

∴PE∥CF。（9分）

【得分分析】（1）“提示：取AB的中點G，連接EG”是本題解決問題的關鍵。要證AE=EF，通常要證這兩條邊所在的三角形全等。而在現有圖形中沒有這樣的全等三角形，就需要構造三角形。條件中給出點E是邊BC的中點，可以得到。觀察圖形，再根據正方形性質，可以知道AB=BC，就明白為什么要“取AB的中點G，連接EG”。其直接目的是證明AG=CE，下一目標是證全等。

（2）此問弱化了條件，把特殊點“中點”換成一般點“邊上任意的一點”，解題基本思路與第（1）問一樣，正確作出輔助線就可以拿1分。為證明全等，找到對應的兩個角相等，就可以各得1 分，最終寫出結論得1 分。我們在證明全等的時候要注意格式的規范，要將全等條件按照全等三角形的判定定理（此解法用的是“ASA”）的順序書寫，在寫△GAE≌△CEF時要按照對應頂點的順序書寫。

（3）我們要注意此問的提問方式。“當K為何值時，四邊形ECFP是平行四邊形，并給予證明。”因此，我們在解答開始就要先說明“當K=時，四邊形ECFP是平行四邊形。”此說明可得1 分。設參數來表示邊長時，我們要注意表達清楚和完整，否則容易造成條件不明確而丟分。另外，就是考驗我們最基礎的運算能力了。我們在解答的最后階段依舊不能放松要求，只有仔細計算，才能確保獲得全部分數。