挖掘問(wèn)題本質(zhì) 巧用模型求解
文/康 敏

解決平行四邊形綜合類問(wèn)題,我們要學(xué)會(huì)結(jié)合圖形抓住已知條件中的關(guān)鍵信息,尋求已知條件的內(nèi)涵,結(jié)合所求的結(jié)論,從前向后分析,再?gòu)暮笙蚯澳嫱疲诰騿?wèn)題的本質(zhì),找準(zhǔn)解決問(wèn)題的關(guān)鍵點(diǎn),最終探究到適當(dāng)?shù)臄?shù)學(xué)模型來(lái)解決問(wèn)題。
例1(2022·江蘇泰州)如圖1,正方形ABCD的邊長(zhǎng)為2,E為與點(diǎn)D不重合的動(dòng)點(diǎn),以DE為邊作正方形DEFG。設(shè)DE=d1,點(diǎn)F、點(diǎn)G與點(diǎn)C的距離分別為d2、d3,則d1+d2+d3的最小值為( )。

圖1
【分析】如圖2,連接CF、CG,求d1+d2+d3的最小值,就是求DE+FC+GC的最小值。但是DE與另兩邊沒(méi)有公共點(diǎn),這就需要把“折線段”的和轉(zhuǎn)化為“直線段”的和,所以要轉(zhuǎn)化線段DE。由四邊形DEFG是正方形,可得DE=EF。結(jié)合圖形,還需要把CG也轉(zhuǎn)換,這里就是難點(diǎn)和關(guān)鍵點(diǎn)。由四邊形ABCD是正方形,得到∠ADC=∠EDG=90°,AD=CD,能推出∠ADE=∠CDG,這樣就聯(lián)想構(gòu)造三角形全等。連接AE,利用“SAS”證明出△ADE≌△CDG,得出AE=CG,把DE+FC+GC轉(zhuǎn)化為EF+FC+AE。所以,當(dāng)A、E、F、C四點(diǎn)共線時(shí),即得最小值。
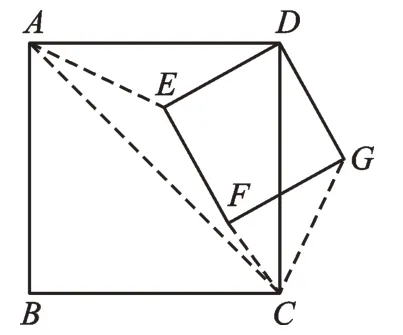
圖2
解:如圖2,連接CF、CG和AE。
∵四邊形ABCD是正方形,四邊形DEFG是正方形,
∴AD=CD,∠ADC=∠EDG=90°,DE=EF=DG。
∴∠ADE=∠CDG。
∴AE=CG。∴DE+CF+CG=EF+CF+AE。
當(dāng)A、E、F、C四點(diǎn)共線時(shí),能取到最小值,即AC的長(zhǎng)。
故選C。
【點(diǎn)評(píng)】本題主要考查正方形的性質(zhì)、全等三角形的證明、勾股定理的運(yùn)用、轉(zhuǎn)換思想等。正確構(gòu)造全等三角形求出邊相等是解決本題的難點(diǎn),此題的全等證明是“手拉手模型”。求順次相連的多條線段和最小,關(guān)鍵是把“折線段”的和轉(zhuǎn)化為“直線段”的和,簡(jiǎn)稱“化折為直”。當(dāng)這幾點(diǎn)共線時(shí),線段和最小,本質(zhì)上運(yùn)用了兩點(diǎn)之間線段最短,體現(xiàn)了由一般到特殊的數(shù)學(xué)思想。
例2(2022·江蘇連云港)如圖3,四邊形ABCD為平行四邊形,延長(zhǎng)AD到點(diǎn)E,使DE=AD,且BE⊥DC。
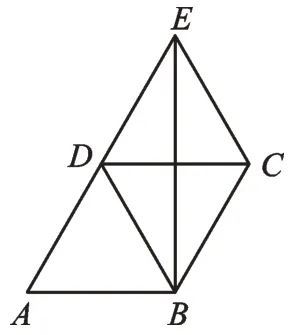
圖3
(1)求證:四邊形DBCE為菱形;
(2)若△DBC是邊長(zhǎng)為2 的等邊三角形,點(diǎn)P、M、N分別在線段BE、BC、CE上運(yùn)動(dòng),求PM+PN的最小值。
【分析】(1)如圖3,先根據(jù)平行四邊形的性質(zhì),得AD=BC和AD∥BC。已知DE=AD,得到BC和DE的數(shù)量關(guān)系和位置關(guān)系,從而證明四邊形DBCE為平行四邊形,再根據(jù)BE⊥DC,即可證得四邊形DBCE為菱形。
(2)如圖4,點(diǎn)P、M、N都是動(dòng)點(diǎn),所以PM+PN是變化的,是“折線段”的和。因此,求其最小值時(shí),要先變“折線段”為“直線段”,即利用轉(zhuǎn)換思想,找不變量。作點(diǎn)N關(guān)于BE的對(duì)稱點(diǎn)N',點(diǎn)N'在DE上,根據(jù)菱形對(duì)稱性得到PM+PN=PM+PN',PM+PN的最小值即為菱形的高。構(gòu)造直角三角形,利用三角函數(shù)即可求得高的值。
(1)證明:∵四邊形ABCD是平行四邊形,∴AD∥BC,AD=BC。
∵DE=AD,∴DE=BC。
∵點(diǎn)E在AD的延長(zhǎng)線上,∴DE∥BC。
∴四邊形DBCE為平行四邊形。
又∵BE⊥DC,∴四邊形DBCE為菱形。
(2)解:如圖4,由菱形對(duì)稱性得點(diǎn)N關(guān)于BE的對(duì)稱點(diǎn)N'在DE上,
∴PM+PN=PM+PN'。
當(dāng)P、M、N'共線時(shí),PM+PN=PM+PN'=MN'。
過(guò)點(diǎn)D作DH⊥BC,垂足為H。
∵DE∥BC,∴MN'的最小值即為平行線間的距離DH的長(zhǎng)。
∵△DBC是邊長(zhǎng)為2的等邊三角形,
∴在Rt△DBH中,∠DBC=60°,DB=2。
【點(diǎn)評(píng)】本題考查了平行四邊形的判定和性質(zhì)、菱形的判定和性質(zhì)、軸對(duì)稱的性質(zhì)、求動(dòng)點(diǎn)類的線段和的最值問(wèn)題,運(yùn)用了轉(zhuǎn)化的思想方法。解決本題的關(guān)鍵是“化折為直”。

