巧用數(shù)學思想 妙解圓類問題

文／仇玉海

數(shù)學思想方法是數(shù)學學科的靈魂和精髓，是解決數(shù)學問題的根本策略。在解決與圓有關的問題時，我們常用的數(shù)學思想方法有：分類思想、方程思想、轉(zhuǎn)化思想等。

一、分類思想

分類思想是研究解決數(shù)學問題的重要方法，它有利于培養(yǎng)同學們嚴謹周密的邏輯思維能力。解題時如果考慮不嚴密，理解不透徹，形成思維定式，就會產(chǎn)生誤解。

例1如圖1，將一塊三角板放置在圓O中，點A、B在圓上，邊AC經(jīng)過圓心O，∠C為直角，∠ABC=60°，P為圓上異于A、B的點，則∠APB的度數(shù)為（ ）。

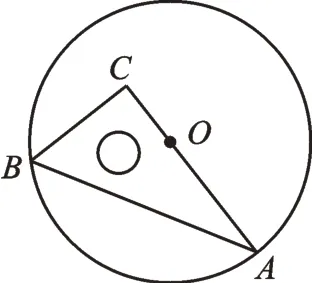
圖1

A.60° B.120°

C.30°或150° D.60°或120

解：連接OB，如圖2。

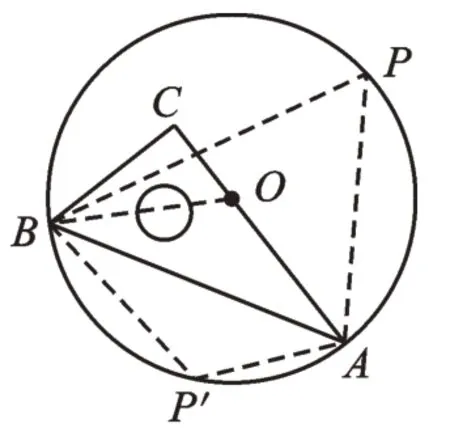
圖2

當點P在優(yōu)弧AB上時，如圖2，連接AP、BP。

∵OB=OA，∴∠OBA=∠OAB=30°。

∴∠AOB=120°。∴∠P=

當點P＇在劣弧AB上時，連接AP＇、BP＇，∠AP＇B=180°-60°=120°。

∴∠APB的值為60°或120°。故選D。

【點評】此題的點P有兩種可能，如果不注意點P所在的位置，就容易遺漏。本題旨在考查思考問題的邏輯性、周密性和全面性。

二、方程思想

方程思想是圓中重要的建模思想之一。抓住問題中的相等關系，我們能巧妙建立起已知量與未知量之間的關系，將相等關系轉(zhuǎn)化為方程（組）。

例2如圖3，AB是圓O的直徑，OD垂直于弦AC于點D，DO的延長線交⊙O于點E。若AC=4，DE=4，則BC的長是（ ）。

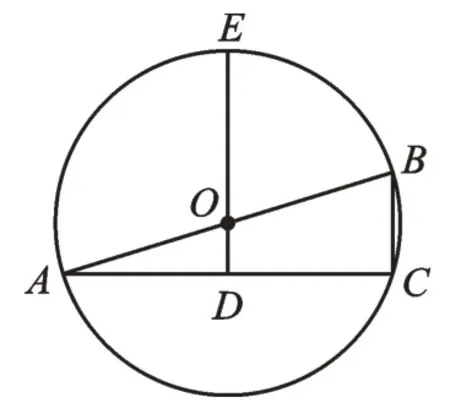
圖3

解：∵AB是圓O的直徑，

∴∠C=90°。

∵OD⊥AC，

∴點D是AC的中點。

∴OD是△ABC的中位線。

∴OD∥BC，且OD=

設OD=x，則BC=2x。

∵DE=4，∴OE=4-x。

∴AB=2OE=8-2x。

在Rt △ABC中，由勾股定理，得AB2=AC2+BC2。

∴（8-2x）2=+（2x）2，解得x=1。

∴BC=2x=2。

故選C。

【點評】本題從分析問題的數(shù)量關系入手，適當設定未知數(shù)，研究數(shù)學問題中已知量和未知量之間的數(shù)量關系，再根據(jù)勾股定理建立方程模型得解。方程思想的獨特優(yōu)勢就是使問題簡單化，方便我們解題。

三、轉(zhuǎn)化思想

轉(zhuǎn)化思想的本質(zhì)是把新問題盡可能轉(zhuǎn)化為能解決或較易解決的問題。轉(zhuǎn)化的基本功能是：化生疏為熟悉，化復雜為簡單，化抽象為直觀，化含糊為明朗。

例3如圖4，點M、G、D在半圓O上，四邊形OEDF、HMNO均為矩形，EF=b，NH=c，則b與c之間的大小關系是（ ）。

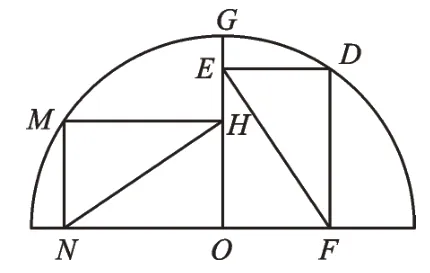
圖4

A.b＞cB.b=c

C.c＞bD.b與c的大小不能確定

解：連接OM、OD，如圖5。根據(jù)矩形的性質(zhì)即可作出判斷。

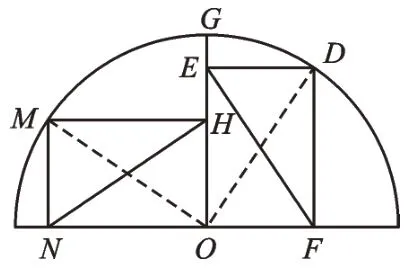
圖5

∵OEDF是矩形。

∴b=EF=OD。同理，c=OM。

∵OM=OD，∴b=c。

故選B。

【分析】本題利用了圓的常用輔助線作法，即連接半徑。根據(jù)矩形對角線相等的性質(zhì)，把兩條線段的關系轉(zhuǎn)化為兩條半徑的關系。轉(zhuǎn)化不僅是一種重要的解題思想，也是一種最基本的思維策略，將復雜問題通過變換轉(zhuǎn)化為簡單問題，將難解的問題通過變換轉(zhuǎn)化為容易求解的問題。