促進思維進階的中考數學專題復習教學模型的建構與實施

武麗虹 葛余常

摘? ? ? 要? ? ?中考數學專題復習是課堂教學的重要形式，但檢視當下初中數學專題復習教學，還存在概念零散化、應用隨意化、訓練淺表化、手段陳舊化等思維進階障礙。基于教學實踐，積極探索學生“自探—自悟”、教師“促探—促悟”雙線并進的思維進階教學活動模式，促進專題復習教學改進。

關 鍵 詞? ? ?思維進階? 專題復習? 中考數學

引用格式? ? ?武麗虹，葛余常.促進思維進階的中考數學專題復習教學模型的建構與實施[J].教學與管理，2023（13）：34-36.

數學專題復習是讓學生從整體上系統地對所學知識、數學思想方法進行聚合，以模塊或單元展開進行教學的一種課型[1]。中考數學專題復習是課堂教學中促進學生知識內化、能力活化、素養優化的重要抓手，但實施專題復習教學的實際情況尚不盡人意，不能完全促進學生落實知識、發展能力、提高素養。為此，本文積極探索促進思維進階的初中數學專題復習教學改進。

一、專題復習中思維進階障礙的表現

1.概念零散化，思維缺乏整體性

專題復習應系統規劃復習和訓練的內容，做到主次分明、重點突出、橫向聯系、縱向貫通，不應是基本知識的簡單重復。但一些教師還熱衷于知識的“灌輸”“平移”，沒有把學生所學的局部的、零散的知識縱橫聯系形成整體結構，沒有在更高層次上對學生所學的重點、難點知識進行內化，未能指向知識形成過程，這樣只能使學生對課本中的知識“原生態”地保留與簡單應用，難以打通學生已有知識技能、思維方法、經驗策略與問題解決之間的通道。

2.應用隨意化，思維缺乏敏捷性

復習離不開解題，但并不在于各種解法的羅列，更重要的是要揭示原理，能夠讓學生有帶得走的經驗。在專題復習中，不少教師不能將教材學習內容轉化為復習教學材料，缺乏教學互動。教師不能給學生思維駐足的時空，學生只能被動接受知識；不能給予學生任何實質性指導以幫助學生消除盲點、清除堵點、突破難點，使學生失去獨立思考和深入探究的機會；不能利用解題引導學生將所學知識內化遷移，學生失去學習興趣；不能利用學習評價去導向、激勵、改進學生的學習。

3.訓練淺表化，思維缺乏深刻性

在專題復習過程中重視知識的落實，加強學生的知識儲備是無可厚非的。但不少教師在專題復習中，受固有經驗程式的影響，不能強化活動和體驗，鮮少幫助學生把符號化的知識“打開”和將靜態的知識“激活”，所開展的還是“常規、常講、常練”的教學方式，滿足于“識記、理解、應用”的淺層學習，導致“常考常錯”現象屢屢發生。專題復習在關注知識和技能的同時，要指向能力發展過程，注重學生學習思維深度提高，促進學生在學習進階中學會同中求異、異中求同、由此及彼、舉一反三，從而提高學生的思維品質和學科素養。

4.方式陳舊化，思維缺乏創新性

培養學生信息素養是“互聯網+”時代賦予學科教學的一項新使命。用技術來推動學習方式的變革，是目前教育信息技術應用主流。但實際操作中不少教師思維固化在傳統的專題復習課堂上，成為大量陳述性知識和程序性知識的持有者和重復者，忽視學生原有的認知圖式，缺少對學生變通思維、發散思維、創新思維等思維能力的培養，導致學生在涉及高階思維的學習活動中表現并不盡人意。因此，應積極變革課堂教學形態，促進學生思維創新，努力幫助學生學會學習，從而提高學生綜合素養。

二、促進思維進階的教學模型建構

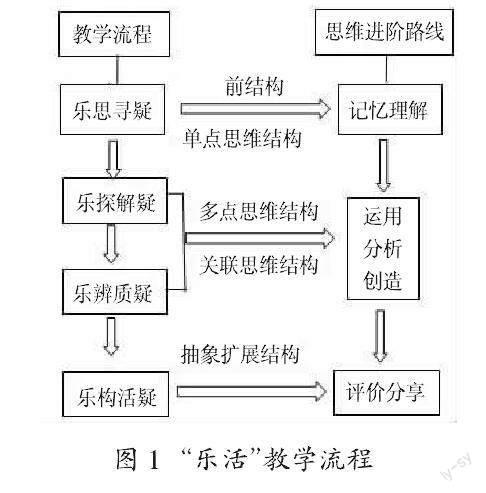
美國心理學家布魯姆（Broome）將認知領域的教育目標由低到高分為六個層次：三種低階思維（記憶、理解、運用）和三種高階思維（分析、評價、創造）。香港大學比格斯教授基于可觀察的學習結果的結構對學生思維進行分類，將學生思維結構分為低階思維（前結構、單點思維結構、多點思維結構）和高階思維（關聯結構、抽象擴展結構）。發展學生的高階思維需要教師在學生思維躍升的節點加以引導，基于深度教學與學科育人的本然統一，在根植課堂教學改進的常態教研中，積極探索促進低階思維向高階思維進階的初中數學“樂活”課堂教學模式，凸顯以“疑”為切口、以“探辨”為手段、以“活”為宗旨、以“技術”為輔助的“樂活”教學流程（如圖1），從而將立德樹人的根本任務落實到數學教學改進中，真正實現數學學科的育人價值。

三、中考數學專題復習教學模型的實施策略

針對目前教學過程中存在的淺層學習問題，教師應著力做學生思維進階的引導者。積極探索學生“自探—自悟”、教師“促探—促悟”雙線并進的思維進階教學活動模式，為促進數學素養整體提高的課程實施提供教學改進新范式。

1.樂思尋疑——思維進階切入點

高階思維是思維進階的目標導向。而思維進階雖然需要教師的協助引導，但更關鍵的是需要學習者本身的深度思考。因此，教學中應設計富有挑戰的問題，既讓不同層次的學生都能基于自身已有學習經驗解決問題，又能作為學生思維進階的“跳板”。通過引發學生充滿張力的思考，激發學生思維活力，助推學生思維從低階向高階爬坡，從而實現學生思維深層發展。

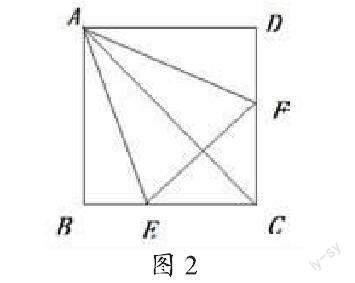
活動1：如圖2，將邊長為a的正方形紙片ABCD折疊，使邊AB、AD都落在對角線AC上，展開后得折痕AE、AF，連接EF。

（1）你能得到哪些特殊的角或三角形？

（2）你能用a的代數式表示△CEF的周長嗎？

專題復習首先要精心選擇源題，通過追根溯源著力引導學生自主思考，激活學生思維。活動1中的折疊操作能加強學生學習體驗，為學生打開直觀想象提供路徑，同時合理設計具有梯度的開放性問題，其目的是以任務驅動讓學生經歷操作、觀察、想象與探究等思維活動，促進正方形知識的深層理解和整體建構。教師通過對圖形有關結論的追問，打開學生思維心扉，加強正方形與三角形知識的關聯，進一步培養學生邏輯思維能力。

2.樂探解疑——思維進階立足點

問題是思維的核心。教師應當通過合適的問題、合理的方式為學習者搭建學習支架，啟發、引導、幫助學生實現思維深度對話。并在知識的新奇處、學習的困惑處、活動的體驗處、情感的共鳴處、經驗的積累處從旁協助，從而延展并外化學生的思維路徑，幫助學生經歷過程構建知識、化解難點發展能力、內化方法提升素養。

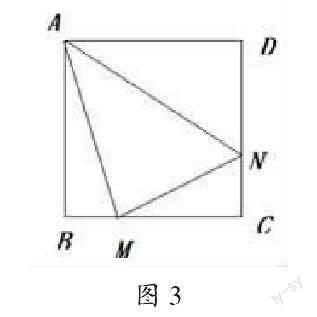
活動2：將圖2中∠EAF繞點A旋轉，使它的兩邊分別交BC、CD于點M、N，連接MN（如圖3）。

（1）此時△CMN的周長是否改變？為什么？

（2）點A到MN的距離是否改變？為什么？

（3）你還能發現什么結論？

活動2是活動1的延續，設計問題鏈引導學生積極思考由此及彼、由例到類，促進學生思維從單點結構向多點結構和關聯結構進階。通過開放性問題讓學生置身思維發散場，培養學生聯想、類比、遷移等思維能力，從而提升學生思維的深度、精度和敏銳度。學生在活動中自主探究分析問題、解決問題并提出問題。

活動3：在以上活動基礎上，過點M作MG⊥AM交CD于H，交AN的延長線于點G，設BM=m（如圖4）。

（1）求CH、CN；

（2）求S△AMN：S△MN；

（3）你還能提出什么問題？

活動3在活動2基礎上引發學生思維形成關聯結構。通過線段設參，加強圖形直觀、邏輯推理和數學運算，豐富學生知識內涵。為學有余力的學生提供進階路徑，發展學生有高階思維參與的理解性學習，培養學生結構化思考、批判性思維、創造性思維等優秀思維品質，讓學生在思維深處體驗更多精彩。

3.樂辨質疑——思維進階著力點

專題復習課堂改進應從“教師中心”向“學生中心”轉變。積極改造和重構知識發現和創生方式，為學生在認知發展的關鍵處提供可靠的腳踏點和支撐點，幫助學生在思維從“此階”向“彼階”不斷攀登過程中質疑辨理，促進學生思維方式從簡單的理解應用邁向分析、評價和創造，進而實現思維品質的進階，促進學生思維形成關聯結構和抽象拓展結構等高階思維結構。

活動4：在圖3中，連接BD分別交AM、AN于點P、Q（如圖5）。

（1）BP、PQ、QD三條線段之間有怎樣的關系？并說明理由。

（2）PQ與MN之間有怎樣數量關系？并說明理由。

（3）連接MQ，你又能發現什么結論？

學習需要階段性跳躍，通過精心安排能打破學科知識與知識邊界的活動，進行活動關聯與知識融通，啟發學生開放思維、質疑思考，習得數學的眼光、思維與表達[2]，促進學生知識、能力的遷移。經歷拾級而上的思維訓練，使學生借力打通初中幾何圖形各知識模塊的隔斷墻，溝通知識單元之間的內外聯系，從課堂之點輻射到課后之面，促使碎片化的知識系統化、整體化、結構化。

4.樂構活疑——思維進階制高點

發展學生的核心素養需要教學積極轉型，教師應通過疑探靈動的活動設計，以開放性、建構性的任務支架幫助學生建立對正方形知識的前理解和后建構，助推學生疏通堵點、破解難點、強化重點、解決疑點，真正實現為“思維進階”而教。

活動5：評價與分享：

（1）本節課我們研究了……

（2）我們經歷了哪些過程？用到哪些方法？

（3）通過本節課的學習，你有什么新的想法？

高階思維根植于學科核心素養，內化于學科學習活動，體現學科關鍵能力，蘊藏情感態度和價值觀念[3]。問題設計著力學生“已知”“未知”“習得”過程，感悟知識的邏輯性、整體性和關聯性。通過“樂構”，幫助學生重建知識、完善結構、促進遷移，助推學生學得更深入、更全面、更合理[4]。借助“活疑”，生發新觀點、引發新認識、獲得新評價，從而讓數學高階思維在體驗和分享中真正創生。

專題復習是學生能力發展的助推器。在學科育人視域下，教師要圍繞興趣激發和潛能開發進行專題復習教學創新，積極探索思維進階的路徑和評價。通過設置具有一定程度的開放性、發散性、思考性和思辨性的問題，充分挖掘數學學科思想、拓展學生的思維深度和廣度，讓學生在復習過程中樂學、活學，進而培養高階思維能力，提高復習效率。

參考文獻

[1] 李君，葛余常.基于混合式學習的初中數學專題復習教學改進策略[J].江蘇教育，2021（51）：62-66.

[2] 武麗虹.指向學科關鍵能力的數學活動教學改進[J].中國數學教育，2021（11）：12-16.

[3] 陳珍妮，吳仁芳.數學高階思維的基本蘊涵、教育價值及培養途徑[J].教學與管理，2022（06）：64-68.

[4] 武麗虹，李君.育人指向的“小結與思考”的教學改進：以“代數式”中“小結與思考”為例[J].中學數學雜志，2022（04）：24-27.

【責任編輯? 郭振玲】