新型混沌電路系統構建及其在故障檢測方向的應用*

覃祖和，秦為民

(1. 廣西機電職業技術學院,南寧市,530007; 2. 汽車仿真與控制國家重點實驗室,長春市,130022)

0 引言

1971年,Chua[1]在變量組合完備性原理的基礎上,通過分析電荷與磁通量之間的函數關系,成功預測了憶阻元件的存在,并在1976年將其分為流控型憶阻器和壓控型憶阻器。2009年,Di等[2-3]將記憶電阻的概念拓展到記憶電容和記憶電感中。因其獨有的儲能特點,含有記憶功能的電路元件被廣泛應用于混沌電路系統的設計中。2008年,Strukov等[4]在Chua電路中使用分段線性憶阻器代替Chua二極管,實現了憶阻混沌振蕩器。在含記憶元件的混沌電路設計方面,大多數學者所設計的復合憶阻電路主要參考一些經典電路,如Chua電路、Wien氏橋震蕩電路等[5-7],由于這些電路的具體實現過程較為復雜,簡單混沌電路的設計就顯得尤為重要:2013年,Bi-Rong[8]提出了使用壓控憶阻的最簡單的混沌電路;2016年,Mou等[9]提出了一個包含兩個電容和三個不同吸引子的混沌振蕩器;2019年,Wang等[10]設計了一種含流控記憶電容的混沌振蕩器。上述的簡單混沌系統的建立只包含一個存儲元件,沒有關于簡單混沌電路的文章提出一個兼容系統可以代表不同的混沌電路。

在拖拉機電路故障檢測領域,現有的拖拉機發動機故障檢測方式為故障特征的識別或整機下線進行電路檢測[11],兩種方式都不能及時地對電路中可能出現的故障進行預警,只能夠在故障發生時或是設備停止運行時對故障電路進行檢測,因此提出一種能夠在故障未發生時的故障預警系統顯得尤為重要。

本文提出了一種可兼容串并聯的小型含憶阻原件的混沌電路系統,并對一類并聯壓控型混沌電路進行了具體混沌分析。分析計算了新型電路系統的分岔方式,利用混沌系統對參數的敏感性,首次將混沌系統的時滯Hopf分岔應用于拖拉機發動機的電路故障檢測中,給出了具體的檢測流程圖和檢測方法,為履帶式拖拉機電路故障檢測提供了一種新的思路和方法。

1 含多個憶阻原件的小型混沌電路系統的建立

本文自主設計了一類含多個憶阻原件的小型混沌電路系統,如圖1所示。

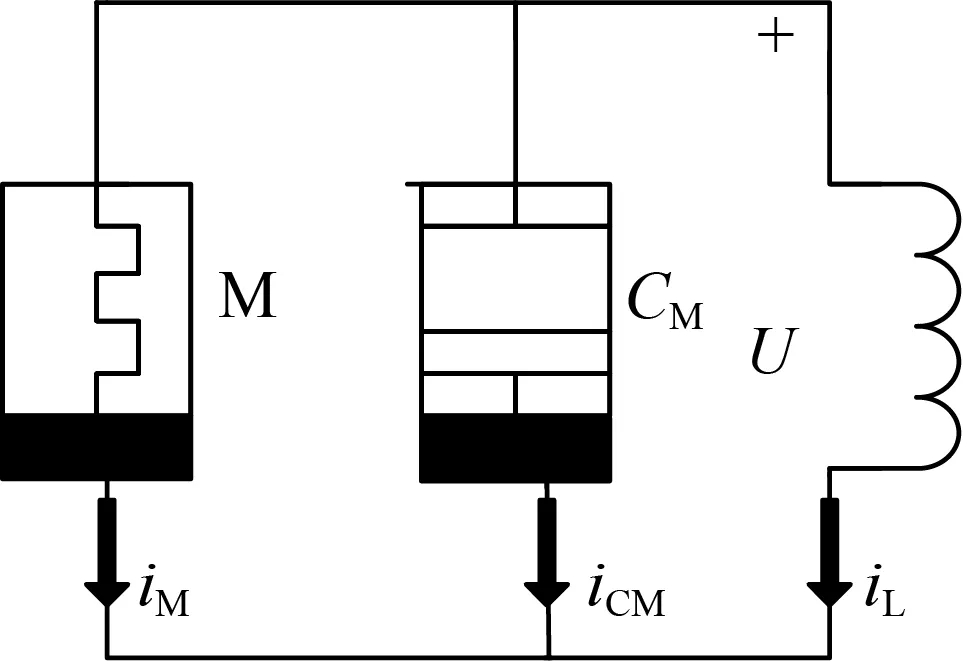
(a) 基于記憶電阻器和記憶電容的并聯電壓控制電路

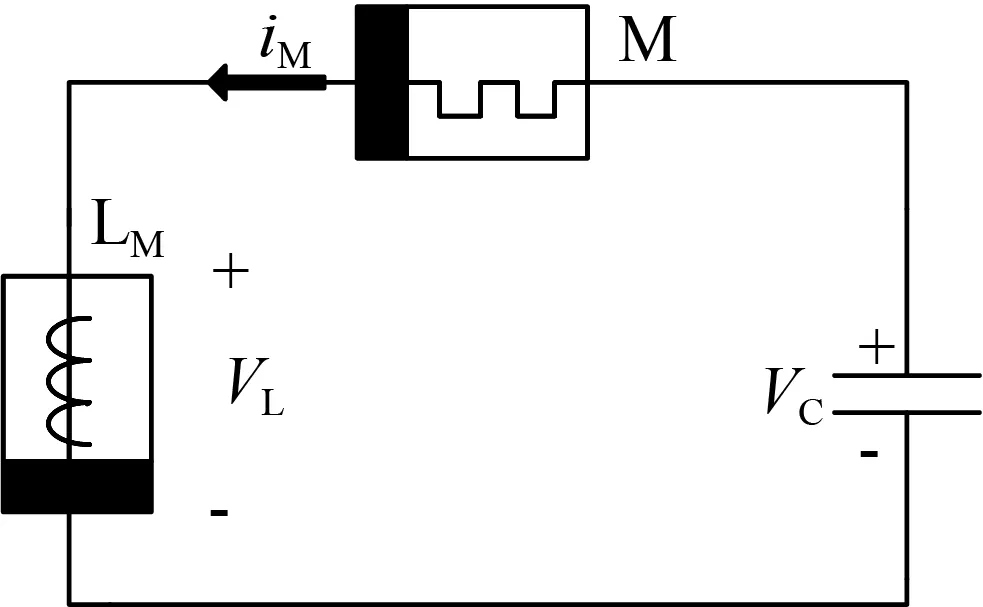
(b) 基于記憶電阻和記憶電感的串聯

綜合圖1分析可得到如下方程。

(1)

式中:k——系統參數;

z——圖1(a)和圖2(b)中通過記憶電容或記憶電感的電荷或磁通。

(a) w-z-x平面相圖

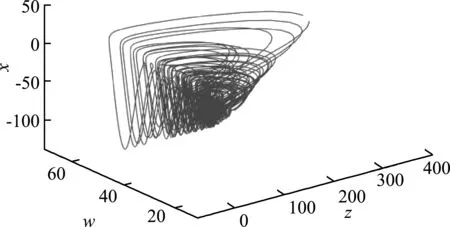
(b) x-y-z平面相圖

G(·),H(·),C(u)能夠通過式(2)、式(3)[12]表示。

A(t)=(m+nσ)B(t)=C(σ)B(t)

(2)

x=G(x,y,t)y

(3)

式中:x——記憶元件的輸出;

y——記憶元件的輸入;

G(·)、H(·)——記憶元件的多樣性。

在式(4)中,本文定義了一類流控型記憶元件和壓控型記憶元件。

式(2)能夠通過式(4)整理得到。

i(t)=(α+βσ1)φ(t)

u(t)=(γ+δσ2)q(t)

(4)

式中:α,β,γ,δ——憶阻元件的系數;

σ1,σ2——磁通和電荷在一定時間內的積分。

將式(2)、式(3)代入式(1)能夠得到如下系統。

(5)

(6)

在式(6)中,令a=0.001,b=0.005,c=0.5,e=4,β=1,d=2,r=0.01,α=1,u=43并通過仿真可以得到圖2,在特定的參數條件下,所構建的電路系統能夠產生混沌吸引子。

2 系統的混沌特性分析

2.1 系統平衡點穩定性分析

令式(6)左邊為0,并通過簡單計算不難得到系統的平衡點為M(0,0,0,u),在系統平衡點處計算能夠得到系統的雅克比矩陣。

其對應的特征方程為

|λE-J*|=λ4+m1λ3+m2λ2+m3λ=0

其中,m1=d-b(α+βu),m2=(r-bd)(α+βu),m3=rd(α+βu),根據勞斯判據[13],能夠得到式(6)的穩定性條件。

當a=0.001,b=0.005,c=0.5,e=4,β=1,d=2,r=0.01,α=1時,有

經過分析可以認為,系統在任意平衡點上(u>1)都難以滿足上述穩定條件,即系統(6)在任意平衡點上都處于不穩定狀態。

2.2 系統混沌特性分析

設系統參數a=0.001,b=0.005,c=0.5,e=4,β=1,d=2,α=1,u=43,通過Matlab仿真計算得到系統的四組混沌序列在參數r變化條件下的李雅普諾夫指數圖像(圖3(a))。本文所建立的電路混沌系統一般具有兩個大于0的李雅普諾夫指數,因此能夠判定本文所建立的混沌系統為超混沌系統。在圖3(b)中,通過仿真計算得到了在參數r變化的條件下,混沌序列z的分岔圖像,仿真結果表明:系統在參數r變化時,會發生分岔現象,并產生混沌。本文通過改變系統參數,分析了在參數a=0.001,b=0.005,c=0.5,e=4不變的條件下,系統的7種不同吸引子狀態,并通過計算得到了每種狀態對應不同混沌序列的李雅普諾夫指數,如表1所示。

表1 系統七種不同類型的吸引子Tab. 1 System of seven different types of attractors

(a) 李雅普諾夫指數圖像

(b) 分岔圖像

2.3 系統在時滯條件下的分岔情況分析

在平衡點為M處將系統線性化,并在y序列中加入時滯項能夠由式(6)得到式(7)。

(7)

式中:τ——新引入的時滯變量,τ>0。

式(7)在平衡點M處的雅克比矩陣及其對應特征方程如式(8)、式(9)所示。

(8)

λ4-αbλ3+rαλ2+(dλ3-αbdλ2+rαdλ)e-λτ=0

(9)

本文將規范型定理和Hopf分岔理論[14]相結合,基于文獻[15]的計算方法計算得到了當參數a=0.001,b=0.005,c=0.5,e=4,β=1,d=2,r=0.01,α=1,u=43時系統的時滯分岔點τ=τ0=0.785 4,并通過仿真計算認為:系統在時滯分岔點附近發生了超臨界Hopf分岔,且當時滯參量τ的值持續增加時,系統吸引子狀態會由穩定變為混沌(τ>1.57)。圖4通過Matlab仿真計算給出了不同時滯條件下的系統吸引子圖像。圖4(a)為系統在時滯分岔點時吸引子的狀態,此時系統在時滯分岔點處產生極限環;圖4(b)為τ=1時系統吸引子的狀態,此時系統仍處于穩定狀態,但極限環消失;圖4(c)為τ=1.57時系統吸引子的狀態,此時系統狀態由穩定變為混沌。通過圖4不難分析認為,隨著時滯參量τ的增加,系統穩定性發生了改變。

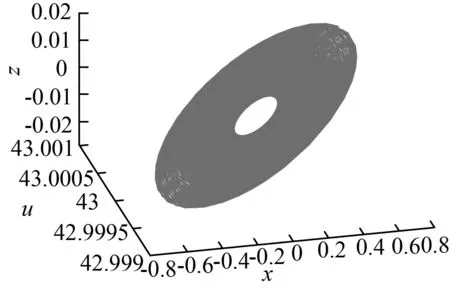
(a) τ=0.785 4

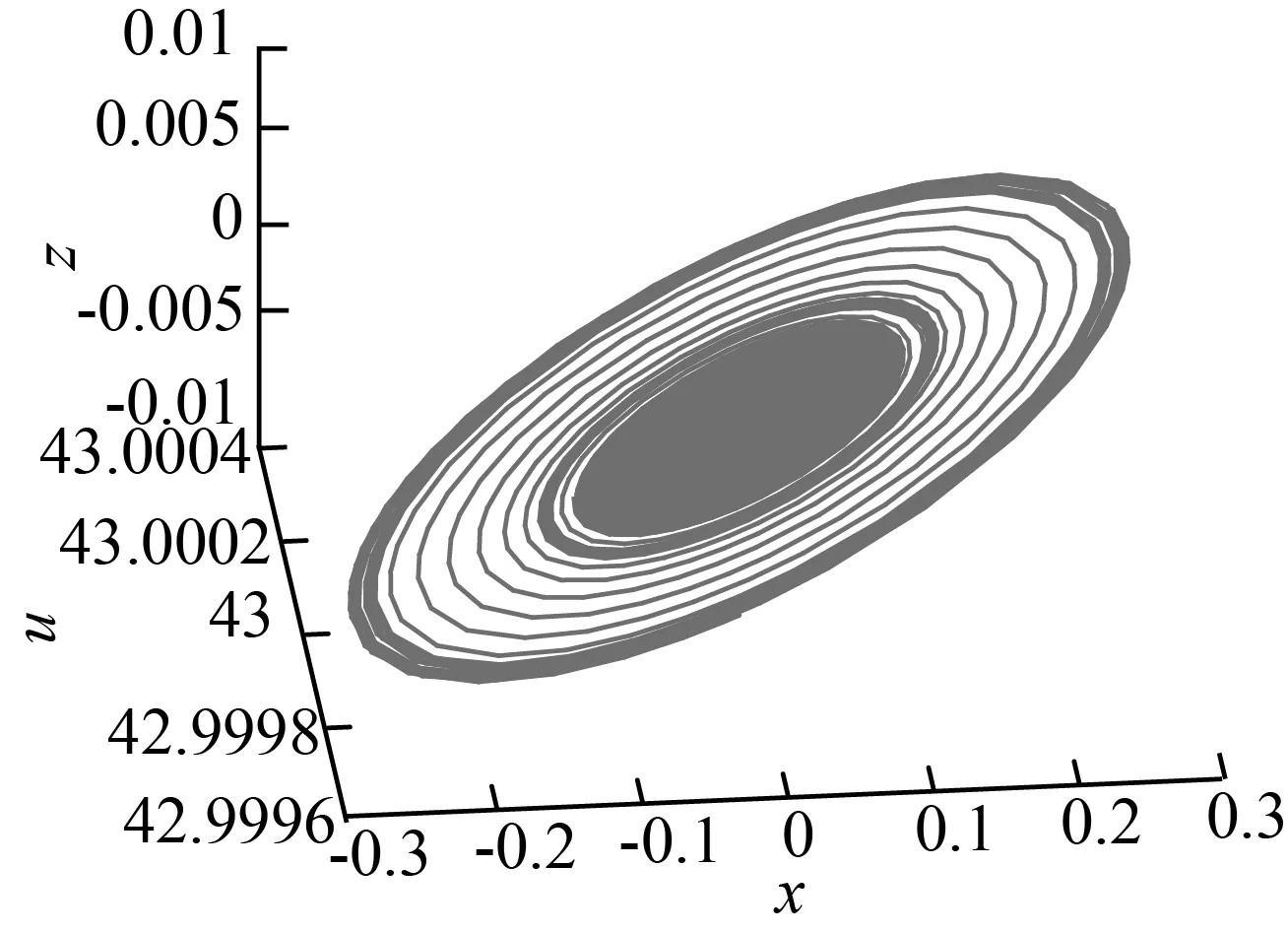
(b) τ=1

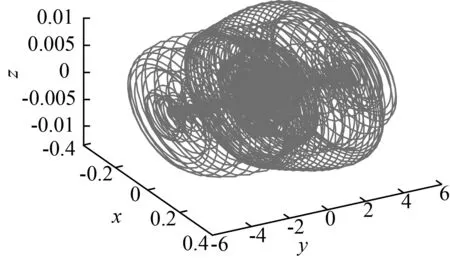
(c) τ=1.57

3 混沌電路系統在履帶式拖拉機電路故障檢測方向的應用

履帶式挖掘機拖拉機的電路故障主要來源于發動機內部控制單元的電路故障[16-17],因履帶式拖拉機發動機內部的故障種類較為復雜,無法從發動機的內部進行故障的檢測,因此只能根據外部電信號的變化來判斷是否有故障產生。本文利用時滯混沌電路系統對時滯參量變化的敏感性,根據電磁閥驅動電路中反饋信號的強弱,來對履帶式拖拉機發動機內部進行短路故障檢測,并能夠在所設定的范圍內做出有效的故障預警。

令故障檢測電路系統中的時滯參量τ=τ0(即系統處于Hopf分岔狀態并產生極限環),記錄系統任意時間序列在時滯參量變化條件下,其李雅普諾夫指數首次由負變正時,系統當前的時滯參數(分別記為τm,τn)。令電磁閥驅動電路中反饋信號做歸一化處理后的值,作為混沌電路系統中的時滯參數,并將τm、τn分別設定為其的上下限,檢測電路中時滯電路設計的部分可以采用電阻匹配的T型LCL濾波器來完成時滯[18],時滯參量的值用式(10)表示。

(10)

其中n表示時滯電路中T型LCL濾波器的個數,通過調節可變電感L和可變電容C的值來改變時滯參量的值。當反饋信號的值偏離了標準值但仍在可控范圍內時(τm<τ<τn),系統發出故障預警并根據預警等級提示檢修;當反饋信號的值越過τm、τn時,會使得電路系統由穩定狀態變至混沌狀態(即對應序列李雅普諾夫指數大于0),并根據反饋信號的值判斷履帶式拖拉機發動機內部是否存在故障,并發出相應的故障警報,混沌電路部分故障檢測流程圖如圖5所示。

圖5 混沌電路部分故障檢測流程圖

圖6展示了基于混沌電路的履帶式拖拉機電路故障檢測原理圖。以葉香美等介紹的挖掘機電子控制單元驅動電路為例,將其輸出信號先做歸一化處理后作為反饋信號輸入履帶式拖拉機故障檢測電路。

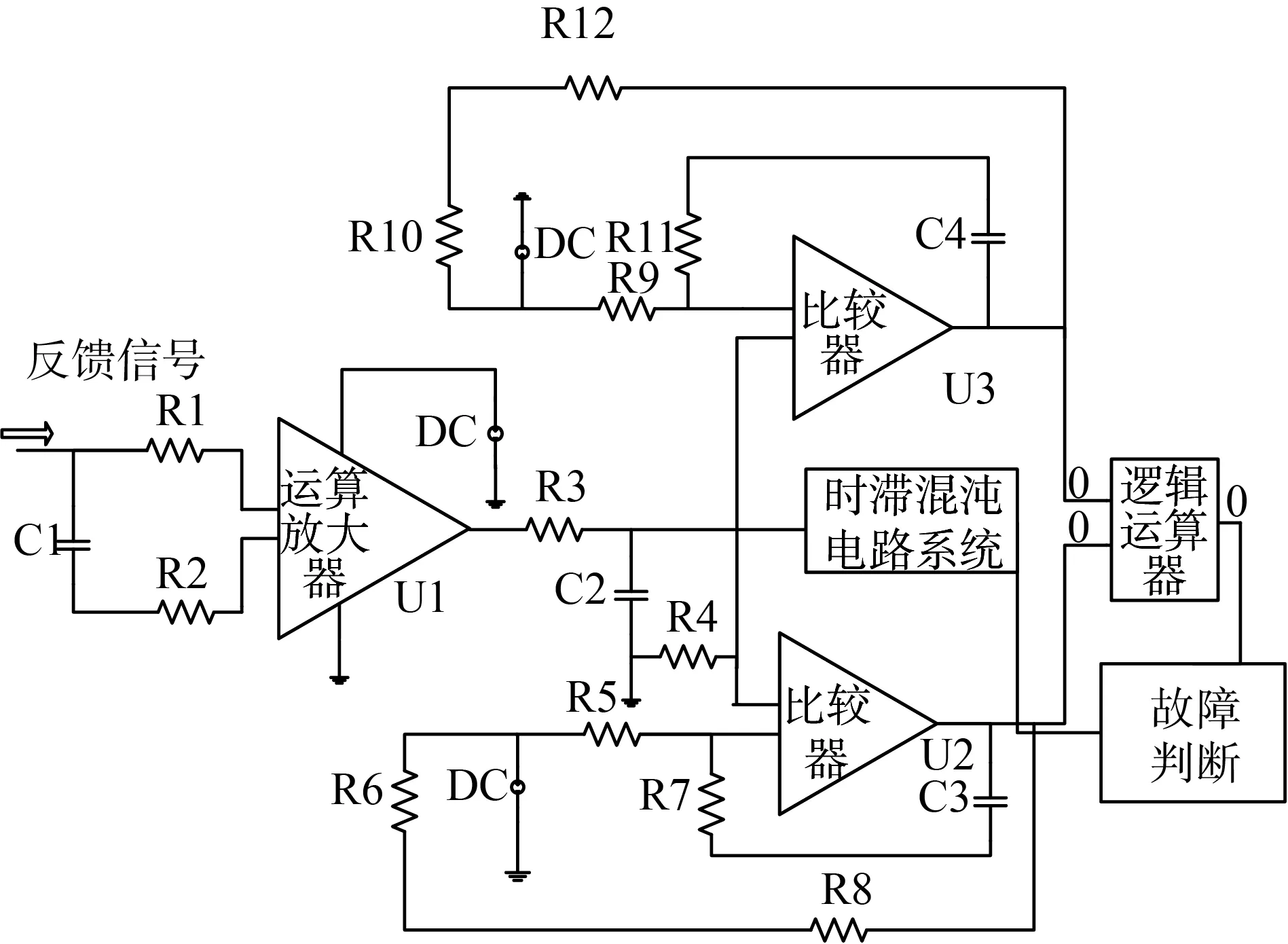
圖6 履帶式拖拉機電路故障檢測原理圖

R1,R2,C1和R3,R4,C2為兩組濾波電路,將由拖拉機電子控制單元驅動電路得到的反饋信號進過濾波后送入運算放大器U1,并將數值處理后的信號分別送入比較器U2、U3以及時滯混沌電路中,首先根據邏輯運算電路判斷反饋信號是否在所設定的范圍區間內(τm,τn),若反饋信號值超過所設定區間則觸發故障警報。若反饋信號值符合所設定范圍,則根據時滯混沌電路系統當前吸引子狀態(序列李雅普霍夫指數)判斷是否觸發相應預警,此處還可以根據序列李雅普諾夫指數的具體數值,通過設置對應的不同時滯參量,來實現對發動機電路系統不同級別的故障預警。

4 結論

1) 研究并建立了一類含多個憶阻元件的新型且易于實現的混沌電路系統,具體分析得到了新建立系統的非線性方程,計算得到了電路系統的混沌特性并通過仿真驗證了系統在不同時滯條件下的穩定性,通過仿真分析表明,系統在時滯分岔點附近發生了超臨界Hopf分岔,且當時滯參量τ的值持續增加時,系統吸引子狀態會由穩定變為混沌(τ>1.57)。

2) 將電路混沌系統的分岔現象應用于履帶式拖拉機發動機的電路故障檢測。基于混沌電路所建立的履帶式拖拉機電路故障檢測系統能夠在實現故障警報的基礎上,通過調整電路參數設置故障預警的范圍(τm,τn),同時基于混沌系統對時滯參數的敏感性設置預警等級,最后通過故障檢測流程圖和履帶式拖拉機電路故障檢測原理圖的可行性分析可以認為,混沌系統能夠應用于履帶式拖拉機發動機的電路故障檢測。