基于Hough變換的月表隕坑檢測算法改進及應用研究

周蘭鳳 李 玲 方 華* 章民融

1(上海應用技術大學計算機科學與信息工程學院 上海 201418) 2(上海市計算技術研究所有限公司 上海 200040)

0 引 言

目前有許多目標需要先進行迅速準確的類圓形檢測,因此,從一幅圖片中快速準確地檢測出類圓,是一個有必要的研究問題,但在圖片數據量日益增大的情況下,所有現有的圓形或橢圓形檢測方法在不同的方面均存在一些問題。

近些年來,人們致力于圓形、橢圓形等的識別,以便能快速從一幅圖片中快速、準確地檢測出類圓,從而進一步進行目標檢測。由于圖像的復雜性以及類圓形參數較多,至今沒有統一的方法來檢測和識別類圓形圖像。對于標準圓檢測,文獻[1]總結了在各種研究中圓檢測常用的幾種算法,如經典Hough算法、隨機Hough算法和廣義Hough算法,并提出將其應用到自動測試織物防水性能中。尚璐等[2]提出從橢圓的弧長著手,橢圓的一般方程及參數通過同一段弧長的邊緣點的位置信息和梯度信息確定,該算法的有效性和檢測時間均優于一般的檢測算法。韋宏強等[3]結合邊界跟蹤算法與Hough變換能夠快速準確地計算出橢圓參數,并形成橢圓邊界鏈碼,消除噪聲及非閉合的數據,達到較好的實驗效果。王艷芳[4]利用橢圓的閉合邊界的特點,給出了一種高效檢測橢圓的方法,提出橢圓邊界鏈碼的概念對橢圓進行邊緣檢測和跟蹤,并使用濾波消除噪聲及非閉合的數據使得邊緣檢測更加清晰,以形成橢圓邊界鏈碼,在鏈碼上尋找對偶點并進行Hough變換,從而精確檢測出橢圓。本文結合類圓形狀的具體特征,應用幾何概念對所要識別的圖像進行灰度轉換及二值化,依次獲取圖像的邊緣,舍棄較為分散的點,構成圖形邊緣,除此之外,使用Hough變換進行類圓參數的提取,得到該類圓形的中心。文獻[15]提出多圓檢測,通過區域生長沿水平和垂直方向搜索候選圓并用Helmholtz原則進行驗證。可以有效檢測重疊圓形輪廓。

Fourie[6]基于噪聲影響和大型復雜圖像,改善了在圓檢測中使用“和諧搜索”(HS),使算法能夠在較大的數據集中穩健地找到多個圓圈。綜上,本文對Hough圓變換做出一系列改進,并對類圓形的具體輪廓進行分析,來對該類圓形進行檢測并識別出邊緣。

1 Hough圓變換

取二維圖像空間中任意圓,圓半徑為R、橫縱坐標分別為x、y,轉換為三維參數空間中的一個點,該過程稱為Hough變換[7],即將二維圖像空間中的邊緣像素點對應為極坐標中的點,然后把三維參數空間中的坐標點元素對應的值依次累加,得到的累積最大值即圓心所在點[8]。

圓的一般方程如下:

(x-a)2+(y-b)2=R2

(1)

具體參數如圖1所示。

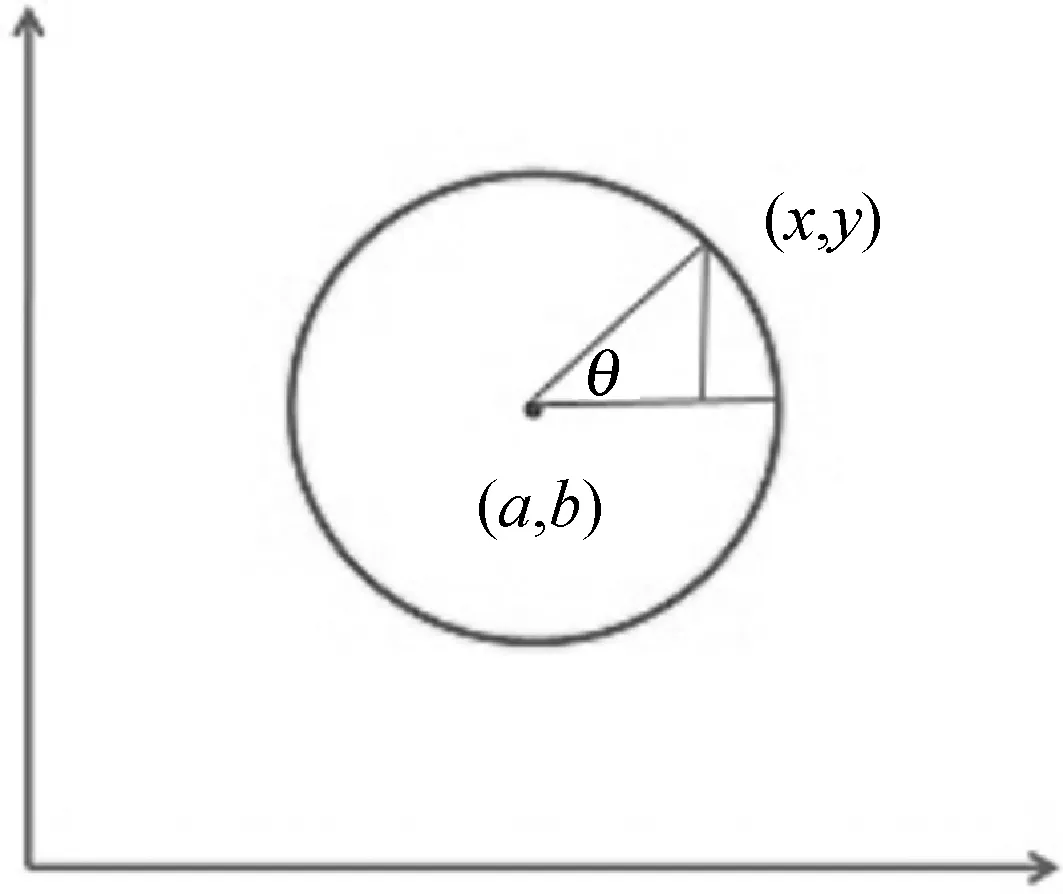
圖1 圓參數示意圖

由圖1可知,(a,b)為該圓圓心,R為該圓半徑。在直角坐標系中,將圓上的點(x,y)轉換到三維空間中,對應的公式如下:

x=a+Rcosθ

y=b+Rsinθ

(2)

在參數空間中任取一邊緣點(x0,y0),以半徑R0映射到參數空間。將這個邊緣點代入式(2),變換后可得:

(3)

式中:θ∈[0,2π)。由式(3)可得,對θ進行遍歷,圖像空間上的點(x0,y0)全部映射到參數空間即為一個圓。由此我們可以推出,在參數空間中的任意一個邊緣點對應到參數空間相連后均生成一個圓[9]。

對原始圖像使用Hough變換進行圓檢測時,具體的檢測步驟如下:

(1) 首先原始圖像進行分析預處理,對圖像做灰度化和二值化操作。

(2) 對目標圖像進行類圓形的邊緣檢測,發現可能的邊界。

(3) 在參數空間ρ-θ中建立一個累加數組,數組初值為0。

(4)
圖像中被檢測類圓形的參數ρ和θ由峰值檢測取得。

參數空間需等分成m行、n列,m為θ的等分數,n為ρ的等分數,并設置累加值矩陣。設置半徑最小刻度、角度最小刻度、半徑的最大值和最小值。遍歷所有的像素點,求出a和b的值。然后判斷(a,b)是否在矩陣(m,n)中,如果(a,b)在該范圍內,累加器加1,從而獲得Hough累積矩陣[10]。

在圓的檢測中需要設置閾值,使用最大累加值確定閾值。搜索超過閾值的點對應的參數即圓的參數。使用不同的閾值將獲得不同的檢測效果,如果閾值設置為0.75,那么大于最大累加值的75%的累積矩陣對應的圓都可以檢測出來[11]。具體圓形檢測原理如圖2所示。

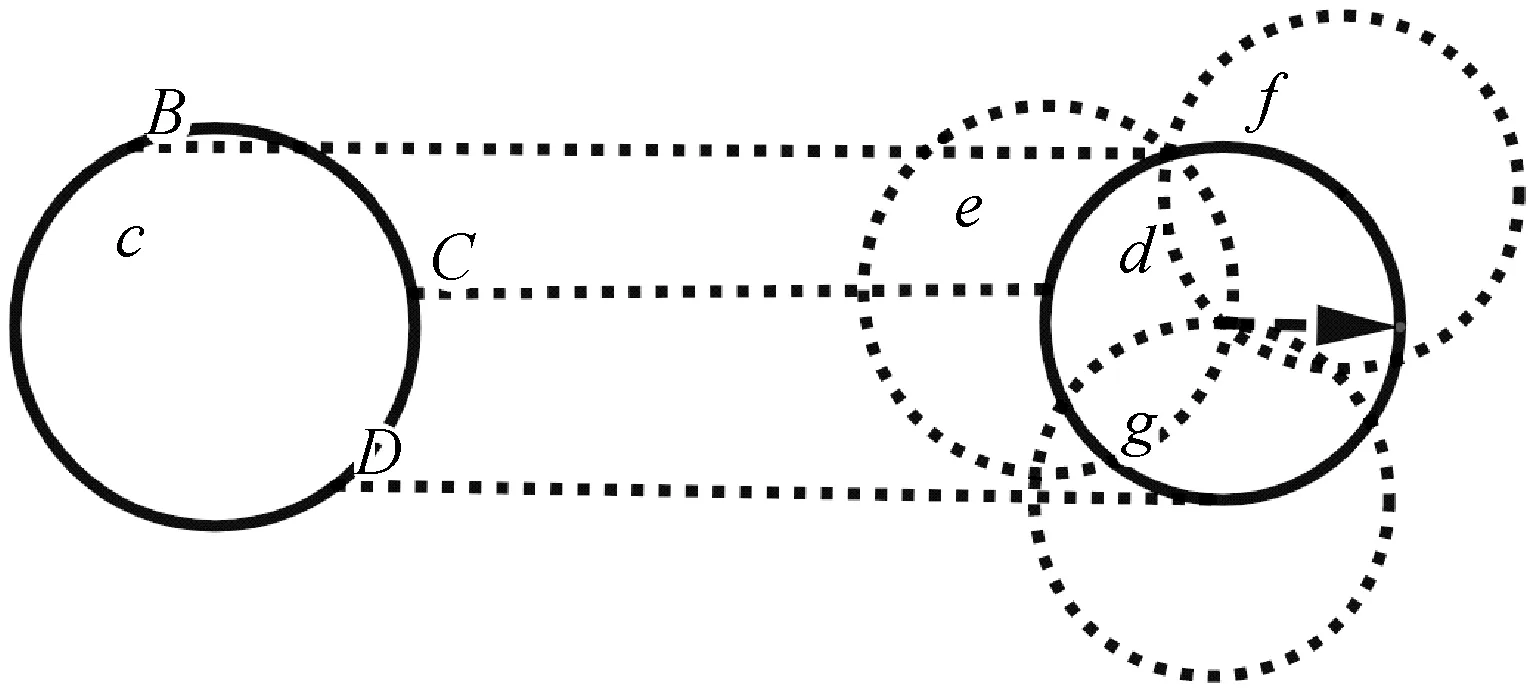
圖2 Hough變換原理

2 本文的類圓檢測改進算法

2.1 系統功能流程

具體算法功能流程如圖3所示。

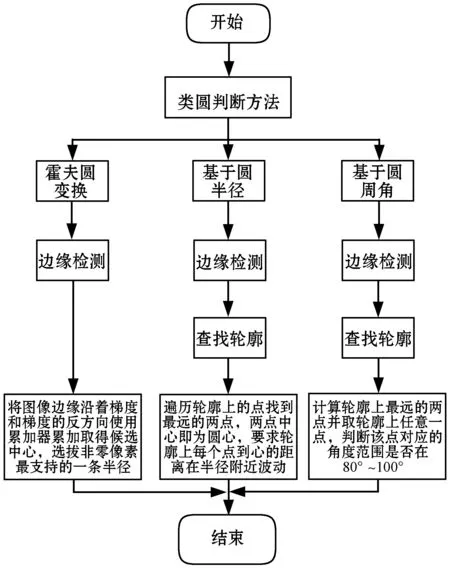
圖3 系統功能流程

2.2 基于圓周角的類圓檢測算法

類圓圓心的獲取方式如下:首先,需要對已經獲取的圖像邊界點進行過濾,以獲取一種連續邊界。假設類圓圓心為O點,在該圖像所在的平面建立一條水平掃描線,依次從該類圓形的邊緣向下掃描,在一維空間中,中點計數采用Hough變換的方法,計數最大值對應的中點即可看作類圓心O[12]。

本文首先通過邊緣檢測查找出該目標圖形的輪廓,依次遍歷輪廓上的每一個點,進行數值比對以獲得輪廓上最遠距離的兩個點,取圓上任意一點(除這兩點之外),最遠距離的兩點的連線視為該類圓形的直徑,判斷該直徑所對的角度范圍是否在80°～100°左右,若是,則對該邊緣進行描繪并給出中心點O。具體參數如圖4所示。

圖4 圓周角a

在該算法中,首先需要對原圖進行邊緣檢測,在保留原有圖像屬性的情況下,顯著減少圖像的數據規模,具體邊緣檢測步驟如下[13]:

(1) 使用高斯濾波去除噪聲達到平滑圖像的目的。

(2) 尋找該類圓形邊界的強度梯度,即根據不同像素值對圖像進行劃分。

(3) 用非最大抑制技術沿邊緣方向追蹤邊緣點來消除邊緣誤檢。

(4) 使用雙閾值的方法來決定可能的邊界,并繪出邊界。

在邊緣檢測成功之后查找圖片中所需要判斷點的輪廓,依次遍歷輪廓上的每一個點來得到輪廓上最遠的兩個點,如圖4所示的AB,在圓上任取一點(除這兩點之外),判斷AB邊所對應的角a是否在80°～100°之間,若該角度在該范圍內,則可以對該圖形進行標記,可用于進一步的識別。

下面給出該算法核心函數的具體實現:

(1) 獲取類圓直徑的平方,和直徑與圓周的輪廓的兩個交點。

1. # 讀其中一個輪廓序列,開始提取,讀其中一個序列中的元

# 素點

2. # 對輪廓上的每一個點進行遍歷,找出最遠的兩個點,作為

# 直徑,中心點為圓心,

3. # 輪廓上任一點,該三點構成圓周角進行判斷,若在90°左

# 右,則畫圓

4. def get_center_diam(data=np.ndarray):

5. max=0

# 直徑的平方

6. point_max=[]

# 輪廓上距離最遠點

7. points=data.tolist()

8. count=len(data.tolist()) # 一個輪廓序列的點個數

9. for i in range(count):

10. points[i][0][0]

11. # i是取第i個點,第一個0去除一層外括號,第二個0是取

# 第一個值

12. length=(points[i][0][0]-points[0][0][0])**2+(points[i][0][1]-points[0][0][1])**2

#判斷直徑

13. if length>max:

14. max=length

15. point_max=points[i][0]

16. return max,point_max,points[0][0]

17. # max為直徑的平方,point_max為距離最遠點,points[0][0]

# 為起始點

(2) 圓周角計算函數如下:

1. def get_angle(pointa=[],pointb=[],pointc=[]):

2. # 定義直徑所在的兩端點和圓上一點

3. a=pointa[0]

4. # 三點構成的三角形,計算所需要余弦角的各個線段長度

5. dx1=pointa[0]-pointc[0]

6. dy1=pointa[1]-pointc[1]

7. dx2=pointb[0]-pointc[0]

8. dy2=pointb[1]-pointc[1]

9. angle_line=(dx1*dx2+dy1*dy2)/cmath.sqrt((dx1*dx1+dy1*dy1)*(dx2*dx2+dy2*dy2)+1e-10)

10. return cmath.acos(angle_line)*180/3.141592653

11. # 采用反余弦公式計算出該角度數

(3) 獲取直徑和具體角度判斷如下:

1. def get_result(max=0,point_max=[],data=np.ndarray):

2. if point_max==[]:

3. return False

4. max=cmath.sqrt(max*1.0)

5. # 獲取直徑長度

6. points=data.tolist()

7. # 轉化為列表形式

8. count=len(data.tolist())

9. # 一個輪廓序列的點個數

10. for i in range(count):

11. # 遍歷輪廓序列,調用角度函數計算該圓周角,判斷圓周#角是否在80°～100°之間

12. if i>0:

13. t=abs(get_angle(points[0][0],point_max,points[i][0]))

14. if t>80 and t<100 and points[i]!=point_max:

15. return True

16. return False

2.3 基于圓半徑的類圓檢測算法

本文算法基于圓半徑的特點,從其中心到其周邊的任何線段都相等,提出若某一圖形上的任何一點到判定后的中點都在該半徑內波動,則該圖形可近似看成圓形。

在此算法中,首先需要通過邊緣檢測識別出該圖像輪廓,依次遍歷該輪廓上的點,由此,可以得到輪廓上距離最遠的兩個點,如圖5所示,AB的中點O假定為圓心,則該兩點間距離可假設為直徑。若在識別出的邊緣上每個點到這個中點的距離在這個半徑數值附近波動,即m和n的長度可近似相等,在此還需對該半徑數據做歸一化處理,以解決直徑大的直徑小的波動范圍不一致問題,由此可近似判定該圖形類圓。

圖5 橢圓參數及點O到曲線邊緣的距離

3 實驗結果分析

本文算法使用Python語言實現,采用Python 3.7、OpenCV 3.4.3.18。本文算法對于圖像的基礎處理步驟如下:代碼首先需要對原圖像進行邊緣檢測,二值化操作后確定該類圓形的邊緣。對于圖像邊緣的任意一個非零點都需要采用Sobel算子,對于參數指定的每一個像素都需要在累加器中疊加并做出標記。累加器圖像的反比分辨為1,Canny邊緣函數的高閾值設置為60,圓心檢測閾值設置為26。圓心檢測閾值需要根據圖像中的圓大小設置,當這幅圖片中的圓越小,那么此值就應該被設置得越小,避免噪聲的產生。在實驗結果上,該類圓的邊緣檢測在實驗中達到了很好的實驗效果。

本實驗在Windows 10系統,基于x64的處理器,具體處理器為Inter(R) Core(TM) i7-10510U CPU @ 1.80 GHz 2.30 GHz上實現,內存大小為12.0 GB。

與Hough圓變換相比,在某些情況下本實驗對于類圓形的檢測成功率較高,第一幅測試圖的具體參數為675×446(24-bit color),該測試圖僅用于測試該算法識別的精確度。第二幅測試圖的具體參數為309×163(24-bit color),該隕石坑測試圖來源于中國探月工程。第三幅數字高程圖(DEM)來源于月球探測軌道器(LRO)和Kaguya數字高程圖的隨機截圖。具體實驗結果如圖6-圖12所示。

圖6 原圖

圖7 Hough圓算法運行結果

圖8 改進算法運行結果

圖9 隕石坑測試

圖10 隕石坑測試結果

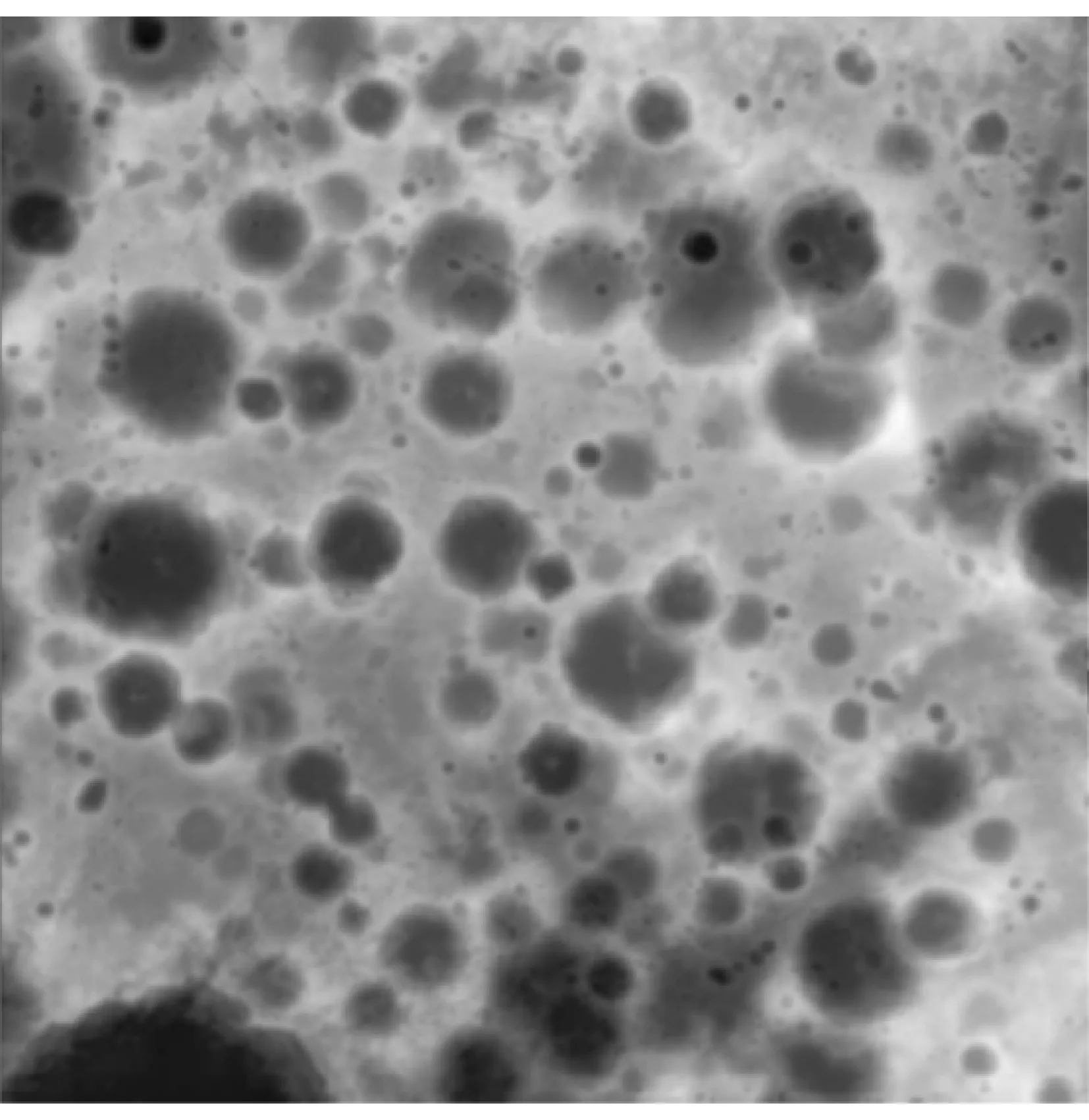
圖11 隕石坑DEM截圖

圖12 測試結果

可以發現該算法對于類似圓形的識別成功率較高,在邊緣清晰度較高的情況下可以準確描繪出圖像的邊緣。但在邊緣清晰度不高的情況下,可以直接對該圖像邊緣進行描繪,對于數字高程圖而言,邊緣檢測的閾值范圍設置為(30,70),閾值分割后得到的圖像的檢測效果較好,如圖12所示。在本實驗中,Canny邊緣檢測算法發揮了很好的作用,對邊緣描繪的準確度較高,但本實驗依舊存在一些不足,對于圓周角變化較大的圓形識別成功率較低且在實際應用中需要對閾值參數進行調節,才可以得到更好的實際應用效果。

類圓形的識別與檢測的算法在工業檢測線、生物醫學監測設備、自動化裝配線上,都有廣泛的應用。文獻[4]將基于直徑累積的Hough變換檢測圓算法應用到人頭輪廓統計和人數統計上。但是該算法在人數較多或人頭輪廓非圓形時,會出現漏檢等情況,且該算法對于直徑的判斷復雜度較高。文獻[15]中提出一種基于曲線擬合的圓形檢測算法,對公路上的交通信號燈進行識別。但該算法僅針對圓形曲線擬合情況來判斷該標志是否是圓心,對圓形的檢測成功率不高。

本文提出的針對圓形基本特點的類圓形檢測算法,對于類圓形檢測成功率能達到90%,在檢測目標數目較多時也能達到很好的識別效果且當圓形重疊時也可以很好地對該類圓形的邊緣進行描繪,具有很好的魯棒性,可應用于公交客流統計、自動識別棒材半徑、自動識別圓形汽車零件,可以滿足工業生產實時性的要求。

本文算法在隕石坑的識別上可以得到很好的應用。在月球車的路徑規劃方面,對于隕石坑的識別與檢測可以給路徑規劃提供較好的數據依據以規避障礙,因此本文算法的提出是有必要的。下一步的研究重點是將深度學習與本文算法結合,期望能在隕石坑的識別中得到很好的效果。

4 結 語

Hough變換在各種形狀檢測方面取得了很好的成果,但在對橢圓以及類圓形的檢測上,由于參數的增多,Hough變換檢測成功率急劇降低。但在很多實際應用中比如人流統計、對人頭輪廓進行檢測計數,以及在月球地形中關于隕石坑的識別上均需要對類圓形進行邊緣檢測。本文結合類圓形的特點,提出兩種檢測方案,應用Canny算法進行邊緣檢測,分別從圓周角和圓心距對該圖形進行判斷,并勾畫出該圖形的輪廓和中心,該實驗在某些時候可以取得較好的實驗效果,在類圓圓心的選取上與標準Hough變換相比,計算復雜度降低,因此具有更高的檢測精度且該算法對于圓形重疊也有很好的檢測效果。將該算法更精確地應用到月球隕石坑的檢測中,將是進一步研究的重點。