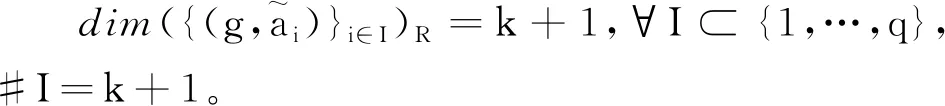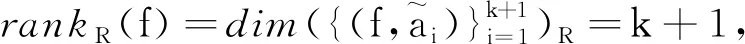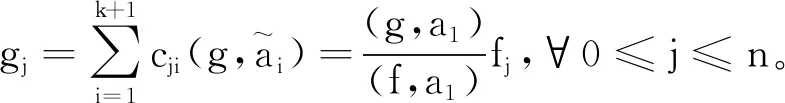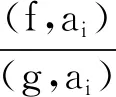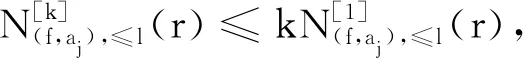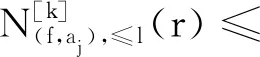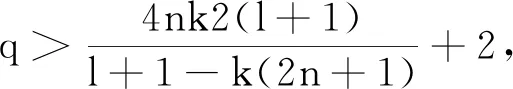亞純映射分擔移動目標的唯一性定理
曹廷彬,阮海洪
(1.南昌大學數學系,江西 南昌 330031;2.陸軍步兵學院,江西 南昌 330103)
最早研究亞純映射分擔移動超平面的唯一性問題要追溯到20年前的文[1-2],接著許多學者也研究這一方向,文章主要集中在文[3-19]。這些年來,關于亞純映射分擔超平面和移動超平面的唯一性問題受到了許多學者的關注。關于這方面最讓人感興趣的研究方向有2個:一個是超平面(移動超平面)的最佳個數是多少?2009年,Chen-Yan[4]得到目前最佳超平面個數q=2n+3。2005年Thai-Quang[5]證明了在亞純映射為線性非退化的條件下移動超平面的個數q=2n2+4n(n≥2)。而2007年,Chen-Li-Yan[6]在沒有要求亞純映射為線性非退化這一情形下,證明了移動超平面的個數q=4n2+2n(n≥2)。2012年,Lü[7]改進了Chen-Li-Yan[6]的結果得到q≥2n2+2n+3。隨后,Thoan-Quang-Duc[3]得到q>4n2+2即可。2013年,Quang-An[10]通過改進Thai-Quang[19]關于移動目標的第二基本定理,并考慮q<4n2+2及截斷重數1的情形,獲得較文[3]更好的結果;另一個是考慮重值,重值的考慮是研究亞純映射分擔超平面(移動超平面)唯一性問題的一個重要課題,也有一些比較好的成果,比如Tu-Wang文[8],Cao-Liu-Cao文[9]等。本文主要在[10]中的兩個關于移動目標的第二基本定理的基礎上考慮重值得到帶截斷重數的第二基本定理,再利用這兩個第二基本定理討論了亞純映射分擔移動目標的唯一性問題。
1 主要結果

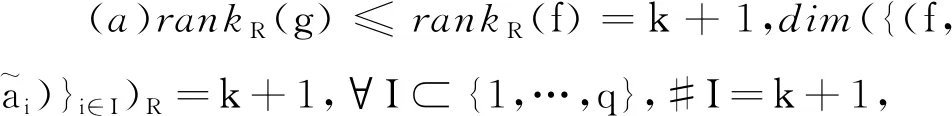
(b)dim{z∈Cm:(f,ai)(z)=(f,aj)(z)=0}≤m-2,1≤i (c){z∈Cm:0<ν(f,aj)(z)≤l}?{z∈Cm:0<ν(g,aj)(z)≤l},1≤j≤q。 (a)dim{z∈Cm:(f,ai)(z)=(f,aj)(z)=0}≤m-2,1≤i (b){z∈Cm:0<ν(f,aj)(z)≤l}?{z∈Cm:0<ν(g,aj)(z)≤l},1≤j≤q。 max{rankR(f),rankR(g)},有f=g。 1)令‖z‖=(|z1|2+…+|zn|2)1/2,z=(z1,…,zn)∈Cm,B(r):={z∈Cm:‖z‖ σ(z):=(ddc‖z‖2)m-1,η(z):=dclog‖z‖2∧(ddclog‖z‖2)m-1在Cm{0}上成立。 3)f:Cm→Pn(C)為一非常數亞純映射。(ω0,…,ωn}為Pn(C)上任意給定的齊次坐標,取Cm上全純函數f0,…,fn使得dimIf≤m-2,其中If:={z∈Cm:f0(z)=…=fn(z)=0},則稱 f=(f0:…:fn)為f的一個約化表示。 令a:Cm→Pn(C)為一亞純映射,且其約化表示a=(a0:…an),定義 4)對Cm上一個除子ν,k,D均為正整數或∞,定義ν的計數函數: 對Cm上的一個亞純函數φ,我們記 為簡便當D=∞時,我們可省略寫上標D。 若對1≤j0<… 則當r→∞,Ta(r)=o(Tf(r)),我們便稱a是(相對f)小映射。 2004年,Ru-Wang[20]引進一個M上非退化的概念,如下: 定義2.1若dim(A)M=n+1,且對任意A中的非空真子集A1,(A1)M∩(AA1)M∩A≠φ,其中(A)M稱為域M上A的線性生成空間,則稱上述A在M上非退化。 若對任意A中的子集A1,#A1=n+1,有dim(A)M=n+1,則稱上述A處于一般位置。 為證明我們的結果,我們還需要以下定理,這些定理在Nevanlinna理論中充當重要角色(見[10,21])。 定理2.1(關于移動目標的第一基本定理)f,a:Cm→Pn(C)為亞純映射且(f,a)≠0,則 Tf(r)+Ta(r)=mf,a(r)+N(f,a)(r) 注意到V(f)的定義與f的約化表示選取無關,且易知rankR(f)=n+1-dimRV(f)。 又由定理2.1和定理2.2可得 令r→∞,有q≤k(k+2)。與已知q≥2k2+2k+3矛盾,因此V(f)?V(g)。從而有 rankR(f)=n+1-dimRV(f)≤n+1-dimRV(g)=rankR(g) 又已知rankR(g)≤rankR(f),于是rankR(g)=rankR(f),從而V(f)=V(g)。 ‖qTf(r)≤ 注意到l>k(k+2)-1,則 再結合定理2.2及上述不等式可得 整理得 ‖qTf(r)≤ ‖qTf(r)≤ 證明結合定理2.3,證明思路與引理3.2類似。 其中ks=q。對任意1≤i≤q,令 且 Pi=(f,ai)(g,aσ(i))-(g,ai)(f,aσ(i)) (3.1) 又由引理3.1,有V(f)=V(g)。 對給定的i(1≤i≤q),由(3.1),以及條件(c),(d)可知對υ∈{i,σ(i)},集合{z∈Cm:0<ν(f,aυ)(z)≤l}(?{z∈Cm:0<ν(g,aυ)(z)≤l})的每個元z0都是Pi的零點,即 (3.2) 又?j∈{1,…,q}{i,σ(i)},則(f,aj)的任意零點z0是Pi的零點(除去一個余維≥2的解析集)。由上述討論,可得 (3.3) 另一方面,由Jensen公式,有 (3.4) 由不等式(3.3),(3.4),得 對上述不等式在i=1,…,q上求和,并由定理2.2和引理3.2,可得 整理得 o(T(r)) 定理1.2的證明假設f?g。記Tf(r)+Tg(r)=T(r)。由定理1.1的證明過程類似可得 整理得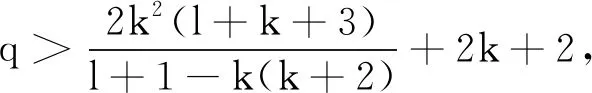
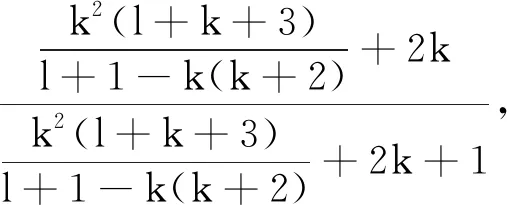
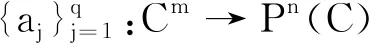
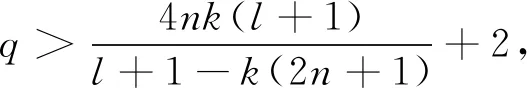

2 Nevanlinna理論中的基本概念和輔助結果








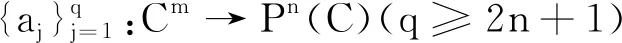
3 引理及定理證明
3.1 引理


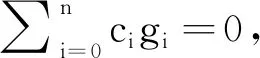


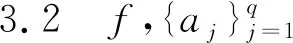
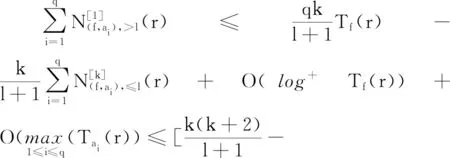

3.2 定理1.1、1.2證明