基于PSO/DE-ELM模型的云貴高原干旱預(yù)測

趙建華 王華 曹雙

摘要：

氣候變化導(dǎo)致西南地區(qū)面臨愈加嚴(yán)重的干旱問題，為準(zhǔn)確預(yù)測該區(qū)域干旱情勢，分別構(gòu)建了粒子群算法（PSO）和差分進(jìn)化算法（DE）優(yōu)化的極限學(xué)習(xí)機(jī)（ELM）模型，并將其應(yīng)用于云貴高原干旱預(yù)測，從預(yù)測精度和特征值模擬能力等方面比較了PSO-ELM模型和DE-ELM模型在云貴高原干旱預(yù)測中的適用性。結(jié)果表明：①PSO-ELM模型和DE-ELM模型均能夠有效預(yù)測云貴高原不同時(shí)間尺度下的干旱狀況，模擬值與實(shí)測值的相關(guān)系數(shù)均在0.75以上，均方根誤差均小于0.65；②兩種模型對最大值、最小值、不同百分位數(shù)等特征統(tǒng)計(jì)值、干旱歷時(shí)和干旱強(qiáng)度的擬合效果較好，能夠有效反映研究區(qū)干旱特征；③相較而言，DE-ELM模型的預(yù)測性能略優(yōu)于PSO-ELM模型，在云貴高原干旱預(yù)測中具有更強(qiáng)的適用性。

關(guān)鍵詞：

干旱預(yù)測； PSO； DE； ELM； SPEI； 云貴高原

中圖法分類號：P426.616

文獻(xiàn)標(biāo)志碼：A

DOI：10.15974/j.cnki.slsdkb.2023.03.002

文章編號：1006-0081（2023）03-0015-07

0 引 言

干旱災(zāi)害是全球范圍內(nèi)影響面最廣、災(zāi)害損失最大的氣象災(zāi)害之一［1-2］，對農(nóng)業(yè)生產(chǎn)、人類生活和社會(huì)經(jīng)濟(jì)發(fā)展均造成了嚴(yán)重的影響［3］。由于干旱影響機(jī)制復(fù)雜、發(fā)展相對緩慢，往往難以對干旱災(zāi)害進(jìn)行系統(tǒng)的評估和預(yù)測［4］，如何科學(xué)地預(yù)防和控制干旱災(zāi)害成為全球各個(gè)國家和地區(qū)面臨的重要挑戰(zhàn)。隨著計(jì)算機(jī)技術(shù)的發(fā)展，機(jī)器學(xué)習(xí)技術(shù)為準(zhǔn)確高效的干旱預(yù)測提供了技術(shù)支撐［5-6］。其中，極限學(xué)習(xí)機(jī)（Extreme Learning Machine，ELM）作為一種學(xué)習(xí)速度快、泛化能力強(qiáng)的單隱層前饋神經(jīng)網(wǎng)絡(luò)，在許多領(lǐng)域得到了廣泛的應(yīng)用［7-9］。但由于ELM自身算法存在缺陷，容易陷入局部最優(yōu)或產(chǎn)生過擬合現(xiàn)象，因此需采用優(yōu)化算法對ELM進(jìn)行優(yōu)化。粒子群算法（Particle Swarm Optimization，PSO）和差分進(jìn)化算法（Differential Evolution Algorithm，DE）作為典型的基于群體進(jìn)化機(jī)制的優(yōu)化算法，在機(jī)器學(xué)習(xí)模型優(yōu)化方面表現(xiàn)較為出色［10-11］，但仍鮮有研究將其應(yīng)用于干旱預(yù)測。本文以中國西南地區(qū)云貴高原為研究區(qū)，分別構(gòu)建了粒子群算法優(yōu)化的極限學(xué)習(xí)機(jī)模型（PSO-ELM）和差分進(jìn)化算法優(yōu)化的極限學(xué)習(xí)機(jī)模型（DE-ELM），并將其應(yīng)用于氣象干旱預(yù)測，揭示了不同智能算法優(yōu)化的極限學(xué)習(xí)機(jī)模型在云貴高原干旱預(yù)測中的適用性。研究成果可為云貴高原防旱減災(zāi)提供技術(shù)支撐。

1 研究區(qū)概況及數(shù)據(jù)來源

1.1 研究區(qū)概況

云貴高原地處中國西南部，位于北緯22°～30°、東經(jīng)100°～111°，包括云南省東部和貴州省全境（圖1）。云貴高原屬于亞熱帶濕潤區(qū)，為亞熱帶季風(fēng)氣候，水量充沛，多年平均降水量約為1 219.7 mm，但受海拔高度和大氣環(huán)流條件的影響，年際年內(nèi)氣候差異顯著，易發(fā)生旱澇。年內(nèi)降水多集中于5～10月，約占全年降水量的85%～95%；最大年降水量與最小年降水量的比值約為1.66。受氣候變化的影響，近半個(gè)世紀(jì)以來云貴高原的干旱頻次和強(qiáng)度均呈現(xiàn)增加趨勢［12-13］。2010年，中國西南五省區(qū)發(fā)生歷史罕見特大干旱，云貴兩省農(nóng)作物受災(zāi)面積達(dá)287萬hm2（4 300萬畝），2 000多萬人出現(xiàn)飲水困難，直接經(jīng)濟(jì)損失達(dá)200億元。連續(xù)嚴(yán)重的干旱威脅區(qū)域糧食和生態(tài)安全，并影響地區(qū)社會(huì)經(jīng)濟(jì)的可持續(xù)發(fā)展。

1.2 數(shù)據(jù)來源

本文采用的氣象資料為中國氣象數(shù)據(jù)網(wǎng)（http：∥data.cma.cn）提供的1971～2016年云貴高原區(qū)域內(nèi)25個(gè)氣象站點(diǎn)的月降水和氣溫?cái)?shù)據(jù)。氣候系統(tǒng)數(shù)據(jù)為中國氣象局國家氣候中心網(wǎng)站（http：∥cmdp.ncc-cma.net/cn/index.htm）提供的1970～2016年的130項(xiàng)氣候系統(tǒng)指數(shù)逐月資料，包括26項(xiàng)海溫指數(shù)、88項(xiàng)大氣環(huán)流指數(shù)以及16項(xiàng)其他指數(shù)。本文所采用的數(shù)據(jù)均通過了一致性與可靠性檢驗(yàn)。

2 研究方法

2.1 標(biāo)準(zhǔn)化降水蒸散指數(shù)

標(biāo)準(zhǔn)化降水蒸散指數(shù)（Standardized Precipitation Evapotranspiration Index，SPEI）［14］基于水量平衡原理，能夠同時(shí)考慮降水和氣溫的影響，并表征不同時(shí)間尺度的干旱狀況，被廣泛應(yīng)用于干旱評價(jià)與預(yù)測［6］。本文采用Thornthwaite方法計(jì)算潛在蒸散發(fā)量，并逐月計(jì)算降水與蒸散發(fā)的差值；采用3參數(shù)log-logistic概率分布對差值序列進(jìn)行正態(tài)化處理，計(jì)算得到3個(gè)月、6個(gè)月和12個(gè)月尺度的SPEI（SPEI-3、SPEI-6和SPEI-12），以此表征不同時(shí)間尺度下云貴高原干旱狀況，并將其作為干旱預(yù)測模型的輸出變量。SPEI的具體計(jì)算原理見參考文獻(xiàn)［14］。

2.2 極限學(xué)習(xí)機(jī)模型優(yōu)化

2.2.1 ELM

極限學(xué)習(xí)機(jī)［15］為典型的基于廣義逆矩陣?yán)碚摰膯坞[含層前饋神經(jīng)網(wǎng)絡(luò)，輸入層與隱含層的權(quán)值和隱含層的閾值可隨機(jī)生成，只需確定隱含層神經(jīng)元個(gè)數(shù)即可獲得唯一解。與傳統(tǒng)神經(jīng)網(wǎng)絡(luò)算法相比，具有學(xué)習(xí)速度快、泛化能力好的優(yōu)點(diǎn)［16］。

若存在N個(gè)樣本（xi，yi），其中xi=（xi1，xi2，…，xin）T∈Rn，yi=（yi1，yi2，…，yin）T∈Rm，ELM隨機(jī)生成輸入權(quán)值w和隱含層偏置b。對于有L個(gè)隱含層節(jié)點(diǎn)，激活函數(shù)為f（x）的ELM輸出式為

yt=∑Li=1βifi（wi，bi，xi）=h（xt）β（1）

式中：t=1，2，…，N；fi為激活函數(shù)；i為節(jié)點(diǎn)；β=（β1，β2，…，βL）T為ELM網(wǎng)絡(luò)中隱含層與輸出層之間的輸出權(quán)值矩陣；h（xt）表示輸出層的輸入數(shù)據(jù)在隱含層對應(yīng)的輸出；bi為第i層隱含節(jié)點(diǎn)的閾值；wi為第i個(gè)輸入層與隱含層的連接權(quán)值。Y=Hβ為ELM目標(biāo)期望的輸出矩陣，H為隱含層輸出矩陣。

2.2.2 PSO/DE-ELM

由于標(biāo)準(zhǔn)ELM的輸入權(quán)值和隱含層閾值是隨機(jī)給定的，參數(shù)的不確定性可能導(dǎo)致模型預(yù)測精度降低或產(chǎn)生過擬合現(xiàn)象［11］。為了提高模型的穩(wěn)定性和預(yù)測精度，本文分別利用粒子群算法（PSO）和差分進(jìn)化算法（DE）對ELM模型的輸入權(quán)值和隱含層閾值進(jìn)行優(yōu)化，將迭代得到的最優(yōu)輸入權(quán)值和隱含層閾值作為ELM模型的參數(shù)進(jìn)行預(yù)測。

粒子群算法（PSO）是一種通過模擬鳥群捕食行為設(shè)計(jì)的群智能全局搜索算法［10］，該方法將問題的解看做空間中的一個(gè)“粒子”的位置，每個(gè)粒子都有專屬的位置和速度，通過計(jì)算各粒子適應(yīng)度值的大小確定個(gè)體和全局極值，并以此更新粒子的位置和速度，在反復(fù)迭代過程中各粒子逐漸趨于全局最優(yōu)解［17］。差分進(jìn)化算法（DE）［18］是一種基于群體的啟發(fā)式全局尋優(yōu)算法。該方法隨機(jī)初始化種群，并隨機(jī)兩個(gè)個(gè)體相減求差進(jìn)行加權(quán)處理，隨機(jī)選取一個(gè)新的個(gè)體對其進(jìn)行交叉變異操作，生成新的個(gè)體；若新個(gè)體優(yōu)于變異前個(gè)體，則保留此個(gè)體，若新個(gè)體適應(yīng)度并未優(yōu)于變異前個(gè)體，則淘汰此變異個(gè)體。

PSO和DE優(yōu)化ELM的具體步驟：① 構(gòu)建ELM模型的樣本數(shù)據(jù)集，采用試錯(cuò)法確定最優(yōu)隱含層神經(jīng)元個(gè)數(shù)，隨機(jī)生成輸入權(quán)值和隱含層神經(jīng)元閾值；② 隨機(jī)設(shè)定種群規(guī)模，將隨機(jī)生成的輸入權(quán)值和隱含層閾值作為種群個(gè)體，利用ELM計(jì)算輸出值，以預(yù)測值與實(shí)測值的均方誤差作為適應(yīng)度函數(shù)，計(jì)算每個(gè)個(gè)體的適應(yīng)度數(shù)值；③ 基于適應(yīng)度計(jì)算結(jié)果更新種群，重復(fù)上述步驟，直至達(dá)到迭代結(jié)束條件。將最終得到的最優(yōu)網(wǎng)絡(luò)輸入權(quán)值和神經(jīng)元閾值代入ELM模型進(jìn)行學(xué)習(xí)和訓(xùn)練。PSO-ELM和DE-ELM的具體流程見圖2。

2.3 云貴高原干旱預(yù)測

將構(gòu)建的PSO-ELM和DE-ELM應(yīng)用于云貴高原干旱預(yù)測。模型輸入?yún)⒖嘉墨I(xiàn)［19］，選取影響云貴高原SPEI-3，SPEI-6和SPEI-12的關(guān)鍵致旱氣候系統(tǒng)指數(shù)，詳見表1。模型輸出為基于云貴高原25個(gè)氣象站點(diǎn)1971～2017年實(shí)測月降水、氣溫?cái)?shù)據(jù)計(jì)算得到的SPEI-3，SPEI-6和SPEI-12，用于表征研究區(qū)實(shí)際干旱狀況。模型的訓(xùn)練期為1972～2012年，共41a，測試期為2013～2017年，共5 a。PSO-ELM和DE-ELM模型的參數(shù)設(shè)置見表2，其中兩種模型在ELM模塊的參數(shù)設(shè)置一致。

2.4 模型性能評價(jià)

為定量評價(jià)模型的預(yù)測精度，本文選取均方根誤差RMSE和相關(guān)系數(shù)CORR為模型精度評價(jià)指標(biāo)，具體計(jì)算公式如下：

RMSE=∑ni=1（xi－yi）2n

（2）

CORR=∑ni=1（xi－x）（yi－y）∑ni=1（xi－x）2∑ni=1（yi－y）2

（3）

式中：xi為模型預(yù)測值，yi為SPEI計(jì)算值；x為預(yù)測平均值，y為SPEI計(jì)算實(shí)測值；n為數(shù)據(jù)個(gè)數(shù)，i=1，2，3，…，n。RMSE和CORR的值均在［0，1］之間，RMSE越接近0且CORR越接近1，則預(yù)測精度越高，反之則預(yù)測精度越低。

本文的干旱預(yù)測模型運(yùn)行次數(shù)為50次，選取50次中各指標(biāo)的平均值評價(jià)模型預(yù)測精度，提高性能評價(jià)的可靠性。

3 結(jié)果與討論

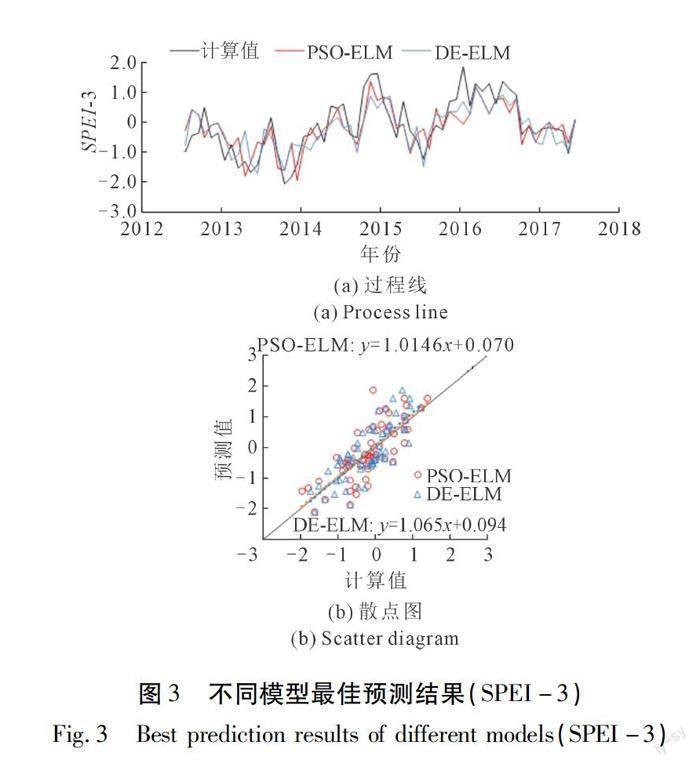
基于PSO-ELM和DE-EL模擬預(yù)測云貴高原干旱狀況，圖3～5為不同時(shí)間尺度不同模型最佳預(yù)測結(jié)果時(shí)間過程線和預(yù)測值與實(shí)際計(jì)算值散點(diǎn)關(guān)系圖，反映了不同模型預(yù)測結(jié)果與實(shí)際計(jì)算結(jié)果的擬合情況。散點(diǎn)圖中實(shí)線為1∶1參考線，虛線為線性擬合趨勢線，趨勢線斜率越接近1且越接近參考線，表明模擬結(jié)果越好。由圖3～5可知，兩種模型對3種時(shí)間尺度SPEI的預(yù)測效果均較好，能夠較為準(zhǔn)確地反映研究區(qū)SPEI的時(shí)間變化過程，預(yù)測值與計(jì)算值相關(guān)性較強(qiáng)，線性擬合斜率在0.85～1.10之間。

采用CORR和RMSE評估模型預(yù)測性能，評價(jià)結(jié)果如圖6所示。為進(jìn)一步評估不同模型在干旱預(yù)測中的適用性，參考相似條件下，文獻(xiàn)［20］基于遺傳算法優(yōu)化極限學(xué)習(xí)機(jī)（GA-ELM）的云貴高原干旱預(yù)測結(jié)果，將GA-ELM模擬得到的CORR和RMSE結(jié)果同樣繪制在圖6中。

通過對比不同模型的CORR和RMSE可知，PSO-ELM和DE-ELM模型在訓(xùn)練期和測試期的模擬精度均能夠滿足精度要求，未出現(xiàn)過擬合或欠擬合現(xiàn)象，表明所構(gòu)建的模型結(jié)構(gòu)合理，且具有較強(qiáng)的泛化能力。對于兩種優(yōu)化模型，訓(xùn)練期CORR均在0.85以上，RMSE均在0.5以下；測試期CORR均在0.75以上，RMSE均小于0.65。根據(jù)參考文獻(xiàn)［20］，相較于標(biāo)準(zhǔn)ELM，GA-ELM在云貴高原干旱預(yù)測中表現(xiàn)出更強(qiáng)的預(yù)測性能，因此本文將PSO-ELM和DE-ELM的計(jì)算結(jié)果與GA-ELM進(jìn)行對比，進(jìn)一步探究PSO和DE對ELM模型的優(yōu)化能力。由圖6可知，不同時(shí)間尺度下，PSO-ELM和DE-ELM在訓(xùn)練期和預(yù)測期的表現(xiàn)均優(yōu)于GA-ELM，測試期CORR分別較GA-ELM提升了5.2%～15.8%和9.6%～17.8%，RMSE分別減小了2.7%～16.7%和7.1%～17.9%，表明相較于GA-ELM，PSO-ELM和DE-ELM模型的預(yù)測性能得到了明顯提升。對比PSO-ELM和DE-ELM的預(yù)測結(jié)果，PSO-ELM在訓(xùn)練期和測試期的CORR在0.767～0.871之間，RMSE在0.423～0.604之間；DE-ELM的CORR在0.799～0.897之間，RMSE在0.411～0.577之間。總體而言，DE-ELM在云貴高原干旱預(yù)測中的表現(xiàn)更優(yōu)于PSO-ELM。

繪制不同時(shí)間尺度SPEI計(jì)算值和不同模型模擬值在測試期的箱型圖，如圖7所示。由圖7可知，對于SPEI-3，PSO-ELM和DE-ELM對最大值的模擬偏小，對最小值的模擬偏大，但對中位數(shù)、上四分位數(shù)（75%）和下四分位數(shù)（25%）的模擬效果相對較好，且DE-ELM的模擬效果相對優(yōu)于PSO-ELM；對于SPEI-6，PSO-ELM對各統(tǒng)計(jì)值的模擬效果均存在一定偏差，DE-ELM模擬結(jié)果的數(shù)據(jù)分布與計(jì)算值的相似程度更高；對于SPEI-12，DE-ELM對數(shù)據(jù)分布的模擬效果同樣優(yōu)于PSO-ELM。綜上，DE-ELM在云貴高原干旱預(yù)測中表現(xiàn)更優(yōu)。

為進(jìn)一步評價(jià)模型預(yù)測結(jié)果的可靠性，本文統(tǒng)計(jì)了不同模型預(yù)測結(jié)果對應(yīng)干旱事件的干旱歷時(shí)和干旱強(qiáng)度。參考基于SPEI的干旱評價(jià)方法，當(dāng)SPEI不大于-0.5時(shí)，認(rèn)為當(dāng)月發(fā)生干旱，發(fā)生干旱的月數(shù)求和為干旱總歷時(shí)，干旱月份SPEI之和的絕對值為干旱強(qiáng)度。計(jì)算測試期不同模型預(yù)測干旱總歷時(shí)和總強(qiáng)度的相對誤差，統(tǒng)計(jì)結(jié)果如圖8所示。

對于SPEI-3，SPEI-6和SPEI-12，測試期實(shí)測數(shù)據(jù)計(jì)算值統(tǒng)計(jì)得到的干旱總歷時(shí)分別為19，23，26個(gè)月；PSO-ELM模擬得到干旱總歷時(shí)分別為20，26，25個(gè)月，相對誤差分別為5.26%，13.04%，-3.85%；DE-ELM模擬得到干旱總歷時(shí)分別為19，24，28個(gè)月，相對誤差分別為0，4.35%，7.69%。對于干旱總強(qiáng)度，3種時(shí)間尺度下PSO-ELM模擬的相對誤差分別為-9.8%，4.5%，-3.21%，DE-ELM模擬的相對誤差分別為-8.43%，-5.55%，-5.21%，相對誤差均在±10%以內(nèi)。兩種模型在干旱歷時(shí)和干旱強(qiáng)度的模擬方面各有優(yōu)劣，但總體誤差均在可接受范圍內(nèi)，能夠有效揭示云貴高原干旱特性。

4 結(jié) 論

本文分別構(gòu)建了基于PSO-ELM和DE-ELM的云貴高原干旱預(yù)測模型，并從模型泛化能力、預(yù)測精度、干旱特征模擬等方面對模型進(jìn)行了綜合評估，驗(yàn)證了模型在云貴高原干旱預(yù)測中的適用性。研究結(jié)果表明：

（1） PSO-ELM和DE-ELM均能夠有效預(yù)測云貴高原干旱狀況；兩種模型對云貴高原不同時(shí)間尺度干旱預(yù)測結(jié)果CORR均大于0.75，RMSE均小于0.65，能夠相對準(zhǔn)確預(yù)測SPEI最大值、最小值、中位數(shù)等各項(xiàng)特征統(tǒng)計(jì)值，預(yù)測干旱總歷時(shí)和總強(qiáng)度相對誤差均在±15%以內(nèi)；

（2） 相較于PSO-ELM，DE-ELM模擬結(jié)果與計(jì)算值的CORR更高，RMSE更小，對SPEI各項(xiàng)特征統(tǒng)計(jì)值的預(yù)測效果更好，在云貴高原干旱預(yù)測中表現(xiàn)更優(yōu)。

參考文獻(xiàn)：

［1］ 王鵬濤.西北地區(qū)干旱災(zāi)害時(shí)空統(tǒng)計(jì)規(guī)律與風(fēng)險(xiǎn)管理研究［D］.西安：陜西師范大學(xué)，2018.

［2］ 朱妮娜.基于GLDAS和GRACE數(shù)據(jù)的塔里木河流域干旱綜合評估［D］.上海：華東師范大學(xué)，2020.

［3］ 符淙斌，溫剛.中國北方干旱化的幾個(gè)問題［J］.氣候與環(huán)境研究，2002（1）：22-29.

［4］ ZHANG Q，YAO Y，WANG Y，et al.Characteristics of drought in southern China under climatic warming，the risk，and countermeasures for prevention and control［J］.Theoretical and Applied Climatology，2019，136（3-4）：1157-1173.

［5］ 趙美言，胡濤，張玉虎，等.基于機(jī)器學(xué)習(xí)模型的海河北系干旱預(yù)測研究［J］.干旱區(qū)地理，2020，43（4）：880-888.

［6］ 米前川，高西寧，李玥，等.深度學(xué)習(xí)方法在干旱預(yù)測中的應(yīng)用［J］.應(yīng)用氣象學(xué)報(bào)，2022，33（1）：104-114.

［7］ 王婷婷，馮起，溫小虎，等.基于極限學(xué)習(xí)機(jī)的干旱區(qū)潛在蒸發(fā)量模擬［J］.中國沙漠，2017，37（6）：1219-1226.

［8］ 葉家豪，魏霞，黃德啟，等.基于灰色關(guān)聯(lián)分析的BSO-ELM-AdaBoost風(fēng)電功率短期預(yù)測［J］.太陽能學(xué)報(bào)，2022，43（3）：426-432.

［9］ 張宇，劉珊.蟻群算法優(yōu)化極限學(xué)習(xí)機(jī)的通信網(wǎng)絡(luò)流量建模分析［J］.甘肅科學(xué)學(xué)報(bào)，2021，33（6）：29-33.

［10］ 黃日勝，黃錫波.基于加速參數(shù)自調(diào)整粒子群算法的物流配送優(yōu)化模型［J］.計(jì)算機(jī)應(yīng)用與軟件，2015，32（10）：328-333.

［11］ 張仙，戴家佳，余奇迪.基于SARIMA-PSO-ELM組合模型的我國鐵路貨運(yùn)量預(yù)測［J］.數(shù)理統(tǒng)計(jì)與管理，2022，41（3）：394-401.

［12］ 張強(qiáng)，鄒旭愷，陳鮮艷，等.考慮多尺度和蒸散影響的新干旱指數(shù)研究——以云南為例［J］.高原氣象，2022，41（4）：909-920.

［13］ 徐海亮.六十年來全國與西南地區(qū)氣象干旱及氣候環(huán)境變化——以云南為例［J］.昆明學(xué)院學(xué)報(bào)，2020，42（2）：24-35.

［14］ VICENTE-SERRANO S M，BEGUERA S，LPEZ-MORENO J .A Multiscalar drought index sensitive to global warming：the standardized precipitation evapotranspiration index［J］.Journal of Climate，2010，23（7）：1696-1718.

［15］ HUANG G B，ZHU Q Y，SIEW C K.Extreme learning machine：Theory and applications［J］.Neurocomputing，2006，70（1/3）：489-501.

［16］ 黃遠(yuǎn)紅，黃清寶.DE-ELM在水煤氣組分濃度軟測量建模中的應(yīng)用［J］.自動(dòng)化儀表，2017，38（2）：77-81.

［17］ 宋劍.基于神經(jīng)網(wǎng)絡(luò)的智能電能表故障預(yù)測研究［D］.南京：河海大學(xué)，2021.

［18］ STORN R，PRICE K.Differential evolution：a simple and efficient adaptive scheme for global optimization over continuous spaces［J］.Clobal Optimization，1997，11（4）：341-359.

［19］ 劉振男.中長期干旱預(yù)測研究：以云貴高原為例［D］.南京：河海大學(xué)，2019.

［20］ 劉振男，杜堯，韓幸燁，等.基于遺傳算法優(yōu)化極限學(xué)習(xí)機(jī)模型的干旱預(yù)測——以云貴高原為例［J］.人民長江，2020，51（8）：13-18.

（編輯：江 文）

Drought prediction of Yunnan-Guizhou Plateau based on PSO/DE-ELM model

ZHAO Jianhua1， WANG Hua2， CAO Shuang2

（1.Suqian Branch of Jiangsu Province Hydrology and Water Resources Investigation Bureau，Suqian 223800，China； 2.Lower Changjiang River Bureau of Hydrological and Water Ｒesources Survey，Bureau of Hydrology，Changjiang Water Resources Commission，Nanjing 210011，China）Abstract：

Climate change has led to a gradual intensification of drought of southwest China.In order to accurately predict the drought regime in this region，the extreme Learning Machine （ELM） models optimized by Particle Swarm Optimization （PSO） and Differential Evolution （DE） were established respectively.In this paper，it used the optimized models（PSO-ELM model，DE-ELM model） to predict drought of Yunnan-Guizhou Plateau.The drought prediction applicability were compared in terms of prediction accuracyand eigenvalue prediction ability.The results showed that ① both PSO-ELM model and DE-ELM model could effectively predict drought conditions in the Yunnan-Guizhou Plateau at different time scales，and correlation coefficient between the simulated values and the measured values were above 0.75，and the root mean square errors were less than 0.65.②The two models fit the maximum，minimum，different percentile and drought duration and drought intensity well，which could effectively reflect the drought characteristics of the study area.③The prediction performance of DE-ELM model was slightly better than that of PSO-ELM model，which had stronger applicability in drought prediction of Yunnan-Guizhou Plateau.

Key words：

drought prediction； PSO； DE； ELM； SPEI； Yunnan-Guizhou Plateau

收稿日期：

2022-04-20

作者簡介：

趙建華，男，高級工程師，主要從事水文水資源分析與論證、防汛防旱等方面的工作。E-mail：zhaojjhh@126.com

通信作者：

曹 雙，男，高級工程師，碩士，主要從事河道治理、防洪研究、水文水資源分析與論證等方面的工作。E-mail：xycaos@qq.com