融合標簽文本的k-means聚類和矩陣分解算法

居曉媛, 汪明艷

(上海工程技術大學管理學院, 上海 201620)

1 引言(Introduction)

推薦算法是以大數據為依托,以用戶行為對象,分析用戶瀏覽的歷史記錄、習慣、偏好,有針對性地為用戶推薦符合其喜好的內容。常見的推薦算法包括協同過濾[1]、基于內容的推薦[2]及混合推薦算法等。協同過濾主要包括兩種:基于內存的協同過濾(Memory-based CF)和基于模型的協同過濾(Model-based CF)。基于模型的協同過濾通過建模的方式模擬用戶對項目的評分行為,其使用機器學習與數據挖掘技術,從訓練數據中確定模型并將模型用于預測未知商品評分。作為常見的基于模型的協同過濾方式,矩陣分解已成為降低數據維數、提取數據潛在特征和減少稀疏性的有效方法。根據矩陣分解可以解決數據稀疏的特點,所以矩陣分解被廣泛應用于推薦系統中。常用的矩陣分解技術包括奇異值分解(SVD)[3]、主成分分析(PCA)[4]、概率矩陣分解(PMF)[5]和非負矩陣分解(NMF)[6]。YAO等提出了一種基于聯合概率矩陣分解的群體推薦方法,能更好地模擬群體推薦問題,在面向群體的推薦問題中取得較好的效果[7]。楊辰等提出一種基于細粒度屬性偏好聚類的新型推薦模型,對項目-屬性關系和用戶-屬性偏好進行建模,基于用戶簇或項目簇采用協同過濾算法生成推薦列表[8]。YUAN等認為隱語義模型(Latent Factor Model)屬于SVD的一種變體,它降低了用戶項目評級矩陣的維數,表示評級矩陣中用戶和項目的潛在特征,其提出了一種混合方面級的隱語義模型(HALFM)優化了全局方面級潛在因子和本地方面級潛在因子,提高了模型預測效果[9]。李淑芝提出一種評論文本和評分矩陣交互(RTRM)的深度模型,取得了較好的推薦效果[10]。邢長征等在推薦模型中加入用戶和項目標簽信息,通過標簽使用次數反映用戶喜好和項目特征,結果表明模型能有效提高跨域推薦的準確性[11]。

盡管學者們從不同的角度改進了矩陣分解算法,在一定程度上提高了算法的準確率和召回率,也有學者關注到項目本身的屬性信息,但是忽略了將用戶的評論標簽與矩陣分解結合使用。本文將矩陣分解算法和k-means聚類算法相結合,首先基于用戶評論的標簽文本構建項目特征畫像和用戶興趣畫像,利用k-means算法將其聚類,找出最優聚類數,然后利用隱語義模型進行矩陣分解,將用戶-評分矩陣進行分解重構并做出推薦,最后在MovieLens數據集上進行實驗,驗證該算法的綜合表現。

2 算法設計(Algorithm design)

針對推薦系統中依賴用戶對項目評分信息的數據稀疏性問題,本文提出一種融合標簽文本的k-means聚類和矩陣分解的推薦算法。矩陣分解的痛點在于隱含特征值的確定,本文將k-means聚類算法引入矩陣分解,確定隱含特征值。主要的算法流程包括以下兩個模塊:一是k-means聚類模塊。在項目潛在特征提取方面,通過對電影標簽文本進行量化處理,采用TF-IDF(Term Frequency-inverse Document Frequency)統計方法構建電影特征畫像,利用k-means聚類方法獲取電影的簇,即項目的潛在特征;在用戶潛在興趣提取方面,將用戶對電影的點評標簽作為用戶興趣標簽,構建用戶的興趣畫像,利用k-means聚類方法獲取用戶的潛在興趣。二是矩陣分解模塊。根據找到的項目潛在特征或者用戶潛在興趣將用戶-評分矩陣進行分解,主要算法流程如圖1所示。

圖1 算法流程圖Fig.1 Algorithm flow chart

2.1 基于k-means的項目潛在特征提取

2.1.1 基于TF-IDF的項目標簽文本量化

TF-IDF是一種針對關鍵詞的統計分析方法,用于評估一個詞對一個文件集或者一個語料庫的重要程度。一個詞的重要程度跟它在文章中出現的次數成正比,跟它在語料庫出現的次數成反比。

首先構建項目特征畫像和用戶興趣畫像,為將項目的文本標簽轉化為計算機可以識別處理的數據結構,然后利用TF-IDF分析提取TOP-n個關鍵詞。TF-IDF計算公式如下:

(1)

(2)

(3)

其中,N表示總的文檔數,Ni表示包含關鍵詞的文檔數,fij表示關鍵詞在文檔中出現的次數,fdj表示文檔中的詞語總數。通過計算每個項目所有標簽詞的TF-IDF值,進行對比,取TF-IDF值中最大的n個關鍵詞作為目標文檔的特征向量,組成項目的特征畫像。

2.1.2 項目標簽內容的k-means聚類

根據項目特征畫像,將屬性特征相似的項目聚在同一簇內,k-means聚類首先選取任意樣本點作為聚類初始中心點,對于每個樣本點,通過計算歐式距離計算該樣本點到每個聚類初始中心點的距離,將其劃分至距離最近的簇中。計算樣本點到中心點的距離公式如下:

(4)

其中,d(mi,ci)表示樣本點mi到聚類中心ci的距離,n表示簇內項目個數。計算每個類別中數據點的平均值,并將得到的平均值作為新的聚類中心,再利用上述公式計算樣本點到新的聚類中心的距離,重新劃分項目簇;經過若干次迭代之后,如果聚類中心不再變化或者變化很小,則可確最終的聚類簇。

對于聚類效果的評估,選擇輪廓系數,其公式如下:

(5)

其中,ai表示樣本點i與同一簇中其他點的平均距離,即樣本點i與同一簇中其他點的相似度;bi表示樣本點i到其他簇中所有點的平均距離,即輪廓系數衡量的是內部距離最小化,外部距離最大化。

利用TF-IDF進行關鍵詞量化后,選擇TF-TDF值最大的30個關鍵詞,聚類區間選擇2—50,觀察聚類效果,如圖2所示,當聚類數為25—40時,聚類效果較好,為檢驗聚類數為25—40的模型評估效果,下面的實驗中將k值取25—40,觀察不同k值的效果。

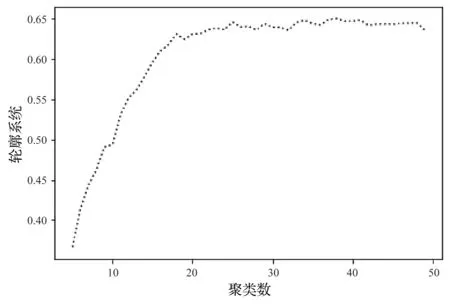
圖2 輪廓系數圖Fig.2 Diagram of contour coefficient

2.2 基于LFM項目潛在特征矩陣生成

2.2.1 矩陣分解

矩陣分解算法是將用戶-項目評分矩陣進行分解,為每一個用戶和項目生成一個隱向量,將用戶和項目定位到隱向量表示的空間上,如圖3所示。將(m×n)維的共現矩陣R分解為(m×k)維的用戶矩陣P和(k×n)維的項目矩陣Q相乘的形式,使得Rm×n=Pm×k×Qk×n。其中,m是用戶數量,n是項目數量,k是隱向量的維度。k的大小決定了隱向量表達能力的強弱。k的取值越小,隱向量包含的信息越少,模型的泛化程度越高;反之,k的取值越大,隱向量的表達能力越強,但泛化程度相應降低。因此,最終目標是求出用戶矩陣P和項目矩陣Q中的每一個值,然后對用戶-項目評分矩陣進行預測。

圖3 矩陣分解過程圖Fig.3 Diagram of matrix decomposition process

基于用戶矩陣P和項目矩陣Q,用戶u對項目i的預估評分如下:

(6)

其中,Puj是用戶u在用戶矩陣P中的對應行向量的第j維,Qji是項目i在項目矩陣Q中的對應列向量的第j維,k表示隱向量維度。

2.2.2 隨機梯度下降

(7)

損失函數的優化使用隨機梯度下降算法,梯度下降的遞推公式如下:

(8)

(9)

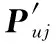
3 實驗設計(Experimental design)

3.1 實驗數據集描述

本文是以電影推薦為具體場景,構建基于電影潛在特征和用戶潛在興趣的推薦模型。本文采用推薦算法中常用的電影數據集MovieLens中的ml-latest-small數據集,包括用戶-電影評分數據集ratings.csv、電影信息數據集movies.csv及電影標簽數據集tags.csv。k-means聚類模塊使用到電影信息數據集movies,格式包括電影ID、標題、類型;電影標簽數據tags.csv包括用戶ID、電影ID、用戶給電影打的標簽、時間戳。矩陣分解模塊應用到用戶-電影評分數據集ratings。數據集描述如表1所示。

表 1 數據集描述Tab.1 Dataset description

3.2 評估指標

3.2.1 均方根誤差(RMSE)和絕對平均誤差(MAE)

RMSE是精確度的度量,用于比較特定數據集的不同模型的預測誤差,RMSE值越小,說明模型具有更好的精確度。

(10)

(11)

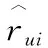
3.2.2 準確率(Precision)和召回率(Recall)

準確率(Precision)和召回率(Recall)的公式如下:

(12)

(13)

其中,TP(True Positive)表示將正類預測為正類;FP(False Positive)表示將負類預測為正類;FN(False Negative)表示將正類預測為負類。

3.3 參數分析

為了得到本文算法的最優參數,首先根據k-means的評估指標輪廓系數選定效果較好的k值為25—40,其余參數的確定進行控制變量實驗,測試重要參數對本文算法效果的影響。實驗隨機選取用戶-評分數據集的80%作為訓練集,剩余20%作為測試集,為防止每次運行結果不一致,設置隨機數種子random_state=1,具體實驗過程如下。

3.3.1 不同k值下模型表現

固定學習率是0.005,正則項系數是0.02,設定迭代次數為15—35次,比較不同k值(取值區間為25—40)的效果。圖4是ml-latest-small數據集迭代次數在[15,35]范圍內,k取不同值對模型效果的影響。由圖4(a)可以看出,不同的k值,迭代次數在[15,25]區間,RMSE值呈下降趨勢,模型效果變好;在[25,35]區間,RMSE值呈上升趨勢,模型效果下降;當k取值為30時,算法的推薦效果最佳。由圖4(b)可以看出,迭代次數在[15,25]區間,MAE值呈下降趨勢,模型效果變好;在[25,35]區間,MAE值呈上升趨勢;k取值為25時,在迭代15次、30次、35次時效果優于k取值為30,但總體而言,k取值為30效果更優,并且在迭代25次時,模型效果最優。因此,根據k-means聚類得出30個聚類時效果最優是成立的,并且此時的最優迭代次數為25次。

(a)不同k值下的RMSE

(b)不同k值下的MAE圖4 不同k值下的模型表現Fig.4 Model performance under different k values

3.3.2 不同正則項系數下模型表現

固定迭代次數為25次,k取值為30時,比較不同學習率及不同正則項系數對模型的影響。圖5是學習率取值在[0.002,0.04]區間,正則項系數的取值不同對模型效果的影響。由圖5(a)可以看出,正則項系數取0.02、學習率在0.005處時,模型效果最優,當學習率大于0.005時,RMSE值呈上升趨勢;正則項系數取0.04或0.06、學習率在0.01處時,模型效果達到最優;正則項系數取0.08或0.1、學習率在0.022處時,與其他正則項系數取值相比,模型效果最好。同樣,由圖5(b)可以看出,正則項系數取0.08或0.1時,模型效果較好。綜合考慮認為,正則項系數取0.1、學習率取0.022時,模型效果最優。

(a)不同正則項系數下的RMSE

(b)不同正則項系數下的MAE圖5 不同正則項系數下的模型表現Fig.5 Model performance under different regularization coefficient

4 實驗結果與分析(Experimental results and analysis)

4.1 比較方法

為了驗證本文提出算法的有效性,選取3種推薦算法模型與本文提出算法進行比較。①非負矩陣分解(NMF)基于傳統的矩陣分解模型,是一種有效的數據分解方法,將用戶-評分矩陣分解為2個非負的小矩陣[12]。②SVD++,在矩陣分解的基礎上考慮用戶瀏覽的歷史記錄,認為用戶瀏覽的歷史記錄對當前項目的評分有一定的影響,將項目間的關聯考慮到模型的評估中[13]。③基于內容的推薦(Baseline)是根據項目本身的標簽信息構建項目特征向量,根據項目間的相似性為用戶做推薦[14]。

在屬性信息層面,非負矩陣分解(NMF)和SVD++兩種方法均屬于矩陣分解,并且沒有考慮項目本身的屬性信息,可以在融合標簽文本的屬性信息層面對本文算法進行有效性驗證。在聚類方法層面,基于內容的推薦僅考慮了項目本身的標簽屬性信息而未引入聚類算法,可以對本文算法引入聚類信息進行有效性驗證。

4.2 比較結果

4.2.1 不同模型的RMSE和MAE對比

對比實驗選擇ml-latest-small數據集,根據控制變量得出的參數結果,選取潛在特征k=30,迭代次數為25,學習率為0.022,正則項系數為0.1。實驗結果如表2所示。非負矩陣分解NMF和SVD++都屬于矩陣分解,但是沒有考慮項目本身的屬性信息;而基與內容的推薦(Baseline)僅考慮項目本身的標簽信息,根據項目間的相似度推薦,本文模型KLFM采用聚類方法,更好地將屬性相似的項目聚類,從而形成項目特征畫像和用戶興趣畫像,能夠更好地為用戶做出推薦。由表2可知,本文模型KLFM的RMSE和MAE均表現較好。

表 2 算法性能對比Tab.2 Algorithm performance comparison

4.2.2 不同模型的準確率和召回率對比

本實驗采用準確率和召回率對各個推薦算法進行評估,具體結果如圖6所示。橫軸表示推薦數量,在ml-latest-small數據集上,本文模型KLFM在推薦數量為[5,25]區間上表現優秀,在推薦的準確率和召回率方面都有了較大幅度的提升,較次優算法分別提升了14.5%和20.7%,模型表現較優。

(b)召回率對比結果圖6 ml-latest-small數據集上性能對比結果Fig.6 Algorithm performance comparison on ml-latest-small

5 結論(Conclusion)

本文針對推薦系統中用戶對項目評分信息的數據稀疏性問題,提出一種融合標簽文本的k-means聚類和矩陣分解的推薦算法。該模型首先對項目信息構建項目特征畫像,利用k-means聚類找出項目的潛在特征數量;然后根據輪廓系數找出最優的k值,利用隱語義模型LFM進行矩陣分解,將用戶-評分矩陣進行分解重構;最后通過實驗分析不同參數對模型效果的影響,根據控制變量法找出最優的模型參數。將本文算法KLFM與其他推薦模型算法進行對照實驗,得出結論:本文模型的RMSE和MAE表現較好,在ml-latest-small數據集中準確率和召回率上較次優算法分別提升了14.5%和20.7%,有效地改善了推薦算法的效果,可以推廣到電商、新聞、社交媒體等其他推薦場景。但是,本文構建項目特征矩陣僅考慮了用戶評論標簽這一屬性,后續研究可以考慮項目的其他屬性,能夠更好地表征項目潛在特征。