湖南地區應力場定量結果及置信區間分析

田優平　沈平　萬永革　唐紅亮　康承旭　姚海東　佘旭明

摘要：基于湖南及其鄰區312個地震的529條P波初動極性數據和32個M_L≥2.8地震的震源機制解，采用格點嘗試法和網格搜索法分別反演得到了湖南地區構造應力場的定量結果和置信范圍。格點嘗試法計算得到的P軸方位和傾伏角分別為102°和10°，T軸方位和傾伏角分別為237°和76°；網格搜索法反演得到的P軸方位和傾伏角分別為100°（置信區間為79°～100°）和5°（置信區間為2°～5°），T軸方位和傾伏角分別為225°（置信區間為204°～225°）和81°（置信區間為81°～82°）。結果表明：湖南地區平均震源機制解表現為逆斷型；主壓應力軸優勢方位為NWW向，傾伏角近乎水平；主張應力軸優勢方位為NE—NEE向，傾伏角較大。對兩種方法得到的研究區應力場結果進行了可靠性分析并與前人結果進行了對比，證實本文結果的可信度較高。

關鍵詞：應力場；格點嘗試法；網格搜索法；置信區間；湖南地區

中圖分類號：P315.727文獻標識碼：A文章編號：1000-0666（2023）04-0483-08

doi：10.20015/j.cnki.ISSN1000-0666.2023.0052

0引言

構造應力場研究是地學研究的重要分支，不僅有助于我們認識地震孕育、發生及其與深淺部構造背景之間的關系，在研究煤油氣等礦產分布、地殼構造演化和地震危險性分析等方面也發揮著重要作用。鄧起東等（1979）根據地震、地質構造和地殼形變等資料，探究了我國構造應力場自晚第三紀以來的基本特征，討論了應力場與板塊運動間的關聯；鄢家全等（1979）通過淺源地震的斷層面解結果等資料討論了我國及鄰區構造應力場區域特征；許忠淮等（1983）在Aki（1966）綜合震源機制解方法的基礎上提出了格點嘗試法，基于P波初動資料推測了華北地區構造應力場的方向，并分析了運用多個小震數據的優勢，汪素云和許忠淮（1985）應用該方法計算了我國東部大陸應力場的方向；謝富仁等（2003）論述了全球構造應力場分布的主要特征；徐紀人等（2008）以大量中強地震的震源機制解為基礎研究了我國大陸地殼應力場與構造運動；萬永革等（2011）提出了綜合震源機制解方法，基于P波初動極性數據反演了中國臺灣地區三維應力場結果，隨后，此方法被廣泛推廣應用（盛書中等，2015；田優平等，2020）；萬永革（2012）首次提出了基于震源機制的網格搜索法求解構造應力場，結果表明該方法在一定程度上提高了應力場的反演精度；田優平等（2014）通過GPS資料討論了三河—平谷地震區的應力特征；吳嘯龍等（2020）利用震源機制解和GPS實測速度場反演得到了喜馬拉雅構造帶應力場結果。

以往對我國華南地塊（張培震等，2003）構造應力場的研究（鄧起東等，1979；鄢家全等，1979；丁旭初，張文濤，1988；徐紀人等，2008；陳益明，1992；謝富仁等，2003；郭良遷等，2012）表明，華南地塊主壓應力軸方位以NWW和NW向擠壓為主。湖南地區位于華南地塊，上述研究中有些雖包含了湖南地區構造應力場結果，但大多是從較大尺度上來勾畫其特征。也有少數學者定量給出了湖南地區應力場的方向：蔣維強等（1992）基于小震震源機制資料，對華南地區地殼應力場進行計算，結果顯示湖南地區主壓應力場方向為NNW向（方位角為334°），主張應力場方向為NEE向（方位角為242°）；汪素云和許忠淮（1985）研究表明，湖南地區P軸方位角為80°，傾角3°，T軸方位角為353°，傾角29°。由于湖南地區地震活動性較弱，因此，學者對該地區的關注度并不高，專門針對湖南地區應力場的研究較少，且由于資料有限，現有湖南構造應力場結果可靠性并不高。近年來，隨著數字化地震臺網的不斷加密，地震監測能力隨之增強，小震資料愈加豐富，使其在構造應力場研究中有著較好的應用前景，如田優平等（2020）利用綜合震源機制解方法反演得到了湖南地區0.2°×0.2°二維構造應力場結果，定性討論了區域應力場總體分布特點，并對湘東、湘西、湘南、湘北、湘中各區應力場特征進行了分析，該方法的優點是既不需要直接求解震源機制解，又能充分利用區域大量的小震數據來計算應力場，但該研究未給出湖南地區總體應力場的定量結果及置信區間。

為了進一步分析湖南地區應力場并給出定量結果和置信范圍，本文拾取2009—2019年湖南及其鄰區312個地震的529條清晰的P波初動數據，首先采用格點嘗試法定量計算湖南地區平均應力場結果，然后計算32個ML≥2.8地震的震源機制解，利用網格搜索法反演得到湖南地區構造應力場及置信區間，最后對比不同方法得到的應力場結果并分析可靠性，探討應力場與區域構造之間的關系，以揭示該區構造應力背景，為區域地震孕育、發生及未來地震趨勢判定提供基礎。

1資料來源

筆者從湖南地震臺網編目震相報告中獲取了2009—2019年湖南及其鄰區（108°～115°E，24°～31°N）42個地震臺站記錄到的632個地震的記錄資料（圖1）。本文使用的地震資料時間跨度在10年以上，這樣既可以充分利用該區域的地震資料，又能改善地震的覆蓋范圍，從而使計算結果相對穩定可靠。為了保證初至P波方向的準確性，舍棄記錄不清晰的數據并重新讀取地震波形資料（田優平，2015；田優平，趙愛華，2016），最終拾取了312個地震的529條清晰的P波初動極性數據。研究區地震震中及活動斷層分布如圖1所示。

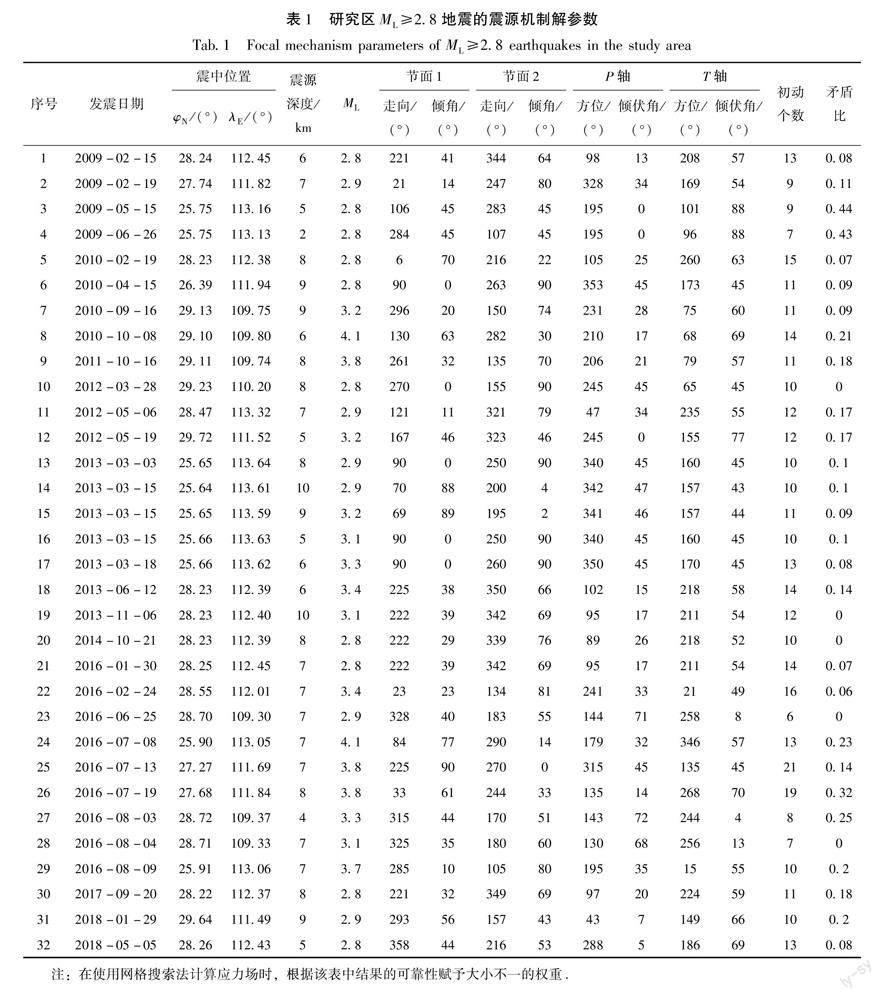
筆者使用基于P波初動數據求解單個地震震源機制解的方法計算了研究區M_L≥2.8地震的震源機制。為了保證震源機制結果的可靠性，本文盡量選取初動個數大于8個、初動較清晰且初動符號在震源球面上分布較為均勻、對震中包圍較好的地震（關鵬虎等，2022），計算得到了32個地震的震源機制解結果（表1）。

2研究方法

2.1格點嘗試法

當P波初動方向資料數量不足或混有錯誤符號，導致在震源球面上難以獲得足以限制兩個節面位置的數據覆蓋時，采用其它解析計算方法求節面解往往依賴于初值選擇，穩定性并不高。鑒于此，許忠淮等（1983）提出了基于P波初動的格點嘗試法，該方法主要根據多個地震在多個源、近臺站上的P波初動方向記錄，確定與平均節面解對應的P、B、T軸，其主要思路是：按照震源雙力偶點源模型，震源機制解可由震源處“震源坐標系”在地平坐標系中的3個獨立變化的角度A_z、i_h、R確定，其中，A_z、i_h分別為臺站方位角和射線離源角。使用格點嘗試法按照10°×10°×10°的步長對這3個角度所有可能的取值逐一進行嘗試，找出一組A_z、i_h、R對應的2個理論正交節面，可將觀測的P波初動方向分為正負相間的四象限，使得與此象限劃分矛盾的觀測數據最少，即矛盾比最低，然后根據觀測數據擬合最佳的一組A_z、i_h、R，即可得到最佳震源機制解。為避免最佳解的不確定性，根據矛盾符號比在最低值和“最低值+5％”之間所有可能的P、B、T軸，計算出平均震源機制解有關參數。

2.2網格搜索法

基于震源機制的網格搜索法是萬永革（2012，2015）、Wan等（2016）提出的以震源機制數據為基礎來反演應力場的一種算法，此方法基于應力張量在斷層面上的滑動方向與剪切應力方向相一致這個準則來求解應力場，并給出在某一置信度下反演參數的置信區間。若研究區有多個不同的震源機制解，則每個解都能給引發斷層運動的應力場應力張量一個約束，通過多個解的互相約束就能夠獲得該區域應力場的平均解。該方法有4大顯著優勢：一是通過全局網格搜索可反演出最優應力場的解，防止局部陷入極值；二是可對多個震源機制數據賦予各不相同的權重；三是與許忠淮等（1984，1985）滑動方向擬合法所采用的準則相比，該方法對地質上已存在薄弱面而發生的地震的計算準確性更高；四是為檢查解的穩定性，除了給出最優解外，還可利用F檢驗得到給定置信度下應力場反演結果的置信區間，可將主應力軸的可信度和反演結果的可靠性定量地展示出來，這在一定程度上提高了應力場的反演精度。

3結果及可靠性分析

3.1格點嘗試法反演結果

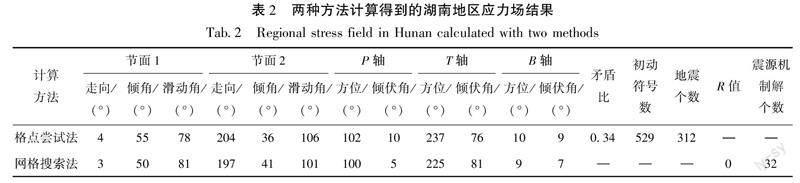
筆者利用湖南及其鄰區312個地震的529條P波初動極性數據，采用格點嘗試法計算得到了研究區平均應力場結果（表2、圖2）。從圖2可以看出，湖南地區平均震源機制解的2個節面走向、傾角、滑動角依次為4°、55°、78°和204°、36°、106°；P軸方位和傾伏角分別為102°和10°；T軸方位和傾伏角分別為237°和76°；初動符號矛盾比為0.34。

3.2網格搜索法反演結果

基于研究區32個M_L≥2.8地震的震源機制解，筆者應用網格搜索法反演了湖南地區構造應力場，并采用F檢驗得到了反演參數的估計空間。應力場計算結果及其三維立體圖見圖3。圖3a中黑色弧線代表所選節面的等面積投影，紅色大箭頭代表P軸的最優方向，藍色大箭頭代表T軸的最優方向，紅色小箭頭代表斷層理論滑動方向，藍色小箭頭代表斷層觀測滑動方向，紅色弧線為最優應力狀態下的最大剪應力節面，綠色弧線為得到的90%置信度下應力場的最大剪應力節面，黃色小箭頭為該節面的最大剪應力方向，P、B、T周圍的封閉曲線代表90%置信度下應力場P、B、T軸的范圍，R為應力比值；圖3b中紅色代表P軸，藍色代表T軸，U、D分別表示上、下。從表2可見，最優解2個節面的走向、傾角、滑動角依次為3°、50°、81°和197°、41°、101°；通過F檢驗給出了P、T、B軸90%置信度下的置信區間，P軸方位、傾伏角最優解分別為100°（置信區間為79°～100°）、5°（置信區間為2°～5°），T軸方位、傾伏角最優解分別為225°（置信區間為204°～225°）、81°（置信區間為81°～82°），B軸方位、傾伏角最優解分別為9°（置信區間為-12°～10°）、7°（置信區間為7°～8°）。表中應力比值R=（S₂-S₃）/（S₁-S₃），S₁、S₂、S₃分別表示最大、中間、最小主壓應力，表中R=0，表示為純擠壓型。

3.3可靠性分析

從表2可以看出，利用格點嘗試法和網格搜索法反演計算得到的湖南地區構造應力場結果比較接近，P、T軸方位、傾伏角等參數相差12°以內，說明兩種方法求解結果均可靠。對于網格搜索法，P、T、B軸方位、傾伏角的置信區間數值波動范圍較小，在22°以內，反演結果相對穩定。

為了進一步檢驗結果的可信度，可使用雙力偶震源機制最小空間旋轉角程序（Kagan，1991）定量計算格點嘗試法和網格搜索法求解結果的差異。在空間坐標下2個震源機制解總能夠通過旋轉特定的角度而達到一致，旋轉的角度越小說明2組解差異越小，旋轉的角度越大則2組解的差異越大。筆者根據萬永革（2008）最小空間旋轉角程序，計算格點嘗試法反演得到的應力場平均解與網格搜索法反演得到的應力場最優解二者的最小空間旋轉角為6.2°，可認為2組解差異很小，一致性好（鄭建常，陳運泰，2012），即兩種方法得到的結果可信度較高。

4討論

圖2和圖3中研究區應力場結果顯示：湖南地區P軸優勢方位為NWW向，大致垂直于區域內主要斷裂。P軸傾伏角接近水平，這與鄧起東等（1979）、鄢家全等（1979）、丁旭初和張文濤（1988）、徐紀人等（2008）、陳益明（1992）、謝富仁等（2003）、郭良遷等（2012）、田優平等（2020）的研究結果較為一致，但與蔣維強等（1992）、汪素云和許忠淮（1985）的結果有所差異，這可能是因為之前學者使用的湖南地區資料有限導致計算的結果與本文不同。湖南地區T軸優勢方位為NE-NEE向，T軸傾伏角較大。根據Zoback（1992）提出的震源機制類別劃分準則，湖南地區平均震源機制解為逆斷型，節面走向同區域主斷裂方向大致相同；湖南地區總體上受NWW向的擠壓應力作用，對該區斷裂具有一定的控制，這可能是該區地震多發生在由湘西自治州、婁邵地區和郴州所形成的NW向空間條帶的重要原因之一。

華南地塊主要受西面的印度板塊和歐亞板塊碰撞作用及東面的太平洋板塊和菲律賓海板塊聯合俯沖作用的控制（虞廷林，1994；蔣維強等，1992；曹海波，范桃園，2016），內部斷裂和活動構造發育，應力場格局復雜多樣。湖南地區處于大陸板塊內部，作為華南塊體的一部分，其區域應力場動力源可能與各板塊的相互運動有關。從本文應力場計算結果來看，湖南地區主要受菲律賓海板塊NWW向的擠壓為主，其次，才受控于太平洋板塊向西推擠的影響，西面的印度板塊和歐亞板塊相互碰撞主要引起青藏高原隆起，加之有云貴高原的阻攔，碰撞產生的影響對湖南地區而言已大幅減弱。綜上所述，各方面的綜合影響，造就了湖南地區現今構造應力場的基本特征。

5結論

本文采用格點嘗試法和網格搜索法反演了湖南地區構造應力場，計算得到P軸和T軸的優勢方向，進而推斷研究區實際構造應力場的大體方向，主要得出以下結論：

（1）采用格點嘗試法計算得到的P軸方位和傾伏角分別為102°和10°，T軸方位和傾伏角分別為237°和76°；采用網格搜索法反演得到的P軸方位和傾伏角分別為100°（置信區間為79°～100°）和5°（置信區間為2°～5°），T軸方位和傾伏角分別為225°（置信區間為204°～225°）和81°（置信區間為81°～82°）。這兩種方法計算所得解的最小空間旋轉角為6.2°，表明結果可信度較高。

（2）湖南地區平均震源機制解表現為逆斷型；主壓應力軸優勢方位為NWW向，傾伏角近乎水平；主張應力軸優勢方位為NE-NEE向，傾伏角較大。

（3）湖南總體上受NWW向的擠壓應力作用，對該區斷裂具有一定的控制，這可能是該區地震多發生在由湘西自治州、婁邵地區和郴州所形成的NW向空間條帶的重要原因之一。

參考文獻：

曹海波，范桃園.2016.長江經濟帶構造應力場特征及動力學環境分析［J］.地質力學學報，22（3）：610-619.

陳益明.1992.華南地區震源機制與應力場特征［J］.華南地震，12（2）：23-31.

鄧起東，張裕明，許桂林，等.1979.中國構造應力場特征及其與板塊運動的關系［J］.地震地質，1（1）：11-22.

丁旭初，張文濤.1988.中國大陸東部現今構造應力狀態［J］.地震學報，10（1）：25-38.

關鵬虎，李斌，李自紅，等.2022.多方法求解中小地震震源機制解的可靠性分析——以山西地震帶3次中小地震為例［J］.太原理工大學學報，53（2）：289-298.

郭良遷，周海濤，杜雪松，等.2012.中國大陸應變應力場研究［J］.華南地震，32（1）：1-10.

蔣維強，林紀曾，趙毅，等.1992.華南地區的小震震源機制與構造應力場［J］.中國地震，8（1）：36-42.

盛書中，萬永革，黃驥超，等.2015.應用綜合震源機制解法推斷鄂爾多斯塊體周緣現今地殼應力場的初步結果［J］.地球物理學報，58（2）：436-452.

田優平，唐紅亮，康承旭，等.2020.綜合震源機制解法反演湖南地區構造應力場的初步結果［J］.地球物理學報，63（11）：4080-4096.

田優平，余達遠，萬永革，等.2014.三河—平谷地震區地球物理特征研究［J］.地球物理學進展，29（4）：1563-1572.

田優平，趙愛華.2016.基于小波包和峰度赤池信息量準則的P波震相自動識別方法［J］.地震學報，38（1）：71-85S.

田優平.2015.近震P波震相自動識別方法研究［D］.北京：中國地震局地球物理研究所.

萬永革，吳逸民，盛書中，等.2011.P波極性數據所揭示的臺灣地區三維應力結構的初步結果［J］.地球物理學報，54（11）：2809-2818.

萬永革.2008.美國Landers地震和Hector Mine地震前震源機制與主震機制一致現象的研究［J］.中國地震，24（3）：216-225.

萬永革.2012.根據震源機制求解構造應力場的網格搜索法［J］.國際地震動態，（6）：19.

萬永革.2015.聯合采用定性和定量斷層資料的應力張量反演方法及在烏魯木齊地區的應用［J］.地球物理學報，58（9）：3144-3156.

汪素云，許忠淮.1985.中國東部大陸的地震構造應力場［J］.地震學報，7（1）：17-32.

吳嘯龍，向洋，湯伏全.2020.基于GPS應變與震源機制解應力反演喜馬拉雅構造帶現今地殼形變特征［J］.地球物理學報，63（8）：2924-2939.

謝富仁，崔效鋒，趙建濤.2003.全球應力場與構造分析［J］.地學前緣，10（S1）：22-30.

徐紀人，趙志新，石川有三.2008.中國大陸地殼應力場與構造運動區域特征研究［J］.地球物理學報，51（3）：770-781.

許忠淮，戈澍謨.1984.用滑動方向擬合法反演富蘊地震斷裂帶應力場［J］.地震學報，6（4）：395-404.

許忠淮，閻明，趙仲和.1983.由多個小地震推斷的華北地區構造應力場的方向［J］.地震學報，5（3）：268-279.

許忠淮.1985.用滑動方向擬合法反演唐山余震區的平均應力場［J］.地震學報，7（4）：349-362.

鄢家全，時振梁，汪素云，等.1979.中國及鄰區現代構造應力場的區域特征［J］.地震學報，1（1）：9-24.

虞廷林.1994.中國東部應力場與板塊運動［J］.地震學刊，（2）：13-17.

張培震，鄧起東，張國民，等.2003.中國大陸的強震活動與活動地塊［J］.中國科學：地球科學，33（S1）：12-20.

鄭建常，陳運泰.2012.基于Langston分解和Hilbert變換約束的區域偏量矩張量反演方法及其應用［J］.地震學報，34（2）：171-190.

Aki K.1966.Earthquake generating stress in Japan for the years 1961 to 1963 obtained by smoothing the first motion radiation patterns［J］.Bull Earthq Res Inst，44（2）：447-471.

Kagan Y Y.1991.3－D rotation of double－couple earthquake sources［J］.Geophys J Int，106（3）：709-716.

Wan Y G，Sheng S Z，Huang J C，et al.2016.The grid search algorithm of tectonic stress tensor based on focal mechanism data and its application in the boundary zone of China，Vietnam and Laos［J］.Journal of Earth Science，27（5）：777-785.

Zoback M L.1992.First－ and second－order patterns of stress in the lithosphere：the world stress map project［J］.J Geophys Res，97（B8）：11703-11728.

Quantitative Results and Confidence Interval Analysis

of the Stress Field in Hunan Region

TIAN Youping SHEN Ping WAN Yongge TANG Hongliang

KANG Chengxu YAO Haidong SHE Xuming YE Shishan

（1.Hunan Earthquake Disaster Risk Prevention Center，Hunan Earthquake Agency，Changsha 410004，Hunan，China）

（2.Institute of Disaster Prevention，Sanhe 065201，Hebei，China）

（3.Hebei Key Laboratory of Earthquake Dynamics，Sanhe 065201，Hebei，China）

（4.Guangdong Earthquake Agency，Guangzhou 510070，Guangdong，China）

Abstract

Based on 529 P－wave polarity data of 312 earthquakes and the focal mechanism of 32 earthquakes with magnitude over 2.8 in Hunan and its neighboring region，we obtain the quantitative results and confidence ranges of the tectonic stress field in Hunan region by using the grid trial method and the grid search method respectively.The mean stress field calculated by the grid trial method shows that the azimuth of P－axis is 102°，the dip angle of P－axis is 10°，and the azimuth and dip angle of T－axis are 237° and 76° respectively.The results from the grid search inversion show that the azimuth and dip angle of P－axis are 100° when confidence interval is 79°-100°，and 5° when confidence interval is 2°-5°，and the azimuth and dip angle of T－axis are 225° when confidence interval is 204°-225°，and 81° when confidence interval is 81°-82°.According to the results of two stress field algorithms，the average focal mechanism proves to be reverse fault in Hunan region.The dominant direction of the principal compressive stress is NWW，and its dip angle is almost horizontal.The dominant direction of the principal tensile stress is NE-NEE，and its dip angle is large.We analyze the reliability of the inversion results from two algorithms，and compare with the previous study，and prove that the results proposed in this paper is of high reliability.

Keywords：stress field；the grid－trial method；the grid－search method；confidence interval；Hunan region