濕氣管線攜液臨界流速預測的機器學習模型*

何鵬 梁裕如 艾昕宇 李森 胡耀強 張成斌

(1. 陜西延長石油(集團) 有限責任公司研究院 2. 克拉瑪依市富城天然氣有限責任公司)

0 引 言

延安氣田位于陜北黃土高原, 地形地貌復雜,管線起伏多且高程較大, 地面集輸采用氣液混輸方式。 在氣田生產中, 井口產液不連續且伴有沖擊流, 產液量波動較大, 在多起伏地形條件下極易造成地面管線低點積液, 嚴重時誘發段塞流, 導致井口回壓增大, 緊急切斷閥頻繁起跳、 管線腐蝕問題突出。 目前有關氣液兩相流攜液特性的研究主要集中在氣井井筒積液方面[1-3], 針對直井、 水平井等氣井穩定帶液開采, 國內外學者進行了相應的試驗及理論分析[4-6], 但對于地面輸氣管線的氣體攜液規律研究相對較少且多集中在力學平衡模型。 李國豪等[7]基于分層流最小剪切應力準則, 建立了濕氣管道積液臨界氣速的計算模型。 潘杰等[8]依據液滴總表面自由能與氣相總湍流動能相等確定了液滴最大粒徑, 建立了橢球形液滴的臨界氣速模型。邢鵬[9]采用CFD 軟件模擬多相流在起伏管道中的流動狀態, 確定了攜液臨界參數。 陳建磊等[10]分析了起伏濕氣管道攜液臨界流速的影響因素, 在G.B.WALLIS[11]液泛經驗公式基礎上, 建立了地面集輸管線攜液臨界氣速計算模型。 以上模型均未考慮地形起伏變化的影響, 并且模型中諸多力學和物性參數受現場工況變化影響較大, 因此計算誤差較大。 為了更好地服務于氣田現場, 筆者采用擴展雙流體分相模型, 基于最小壓力梯度法結合均勻設計和BP 神經網絡, 建立了地面起伏管線攜液臨界流速預測模型, 以期更好地指導濕氣管道的設計和安全運行。

1 攜液臨界流速計算方式確定

目前針對管線攜液臨界流速計算的方法主要集中在最小壓力梯度、 液滴、 液膜模型3 種。 基于液滴和液膜模型建立的力學模型計算參數較多(曳力系數、 氣液界面張力和摩擦因數、 氣-壁摩擦因數等) 且受流型轉換影響較大, 在預測起伏管線攜液臨界流速時適用性較差, 準確性較低。 氣液兩相在管道流動中產生的壓降主要包括剪切摩阻和重力損失, 伴隨管內流量變化, 管道壓力梯度存在最小值。 最小壓力梯度下氣相表觀流速即為攜液臨界流速。 最小壓力梯度法計算相對簡單且易于工程實踐, 因此選擇其作為攜液臨界流速的計算基礎。

筆者結合延安氣田Y439 井區輸氣管網現場工況, 對起伏管線攜液臨界模型進行研究。 該井區天然氣組分見表1。 對井區內管道的上下傾角進行統計發現, 其管線傾角主要分布在0.5°～45.0°。

表1 Y439 天然氣組分表%Table 1 Natural gas composition of the Y439 well district%

以管線長度1 km (上下坡相同), 管徑60 mm, 管段傾角20° (上下坡相同), 運行壓力5 MPa, 運行溫度20 ℃, 天然氣標準狀況下體積含水1.340 5 m3/104m3工況為例, 采用擴展雙流體分相模型對起伏管線(幾何模型見圖1) 水力、 熱力參數進行計算。 其控制方程主要包括質量守恒方程、 動量守恒方程以及能量守恒方程:

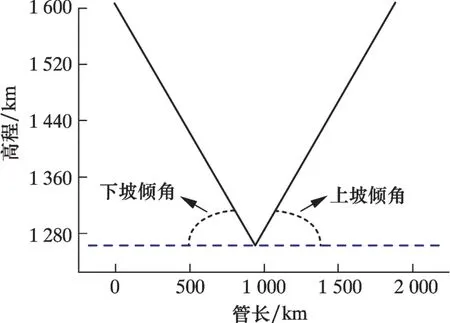
圖1 幾何模型Fig.1 Geometric model

式中:V為各相體積分數,%;G為各相質量源,kg/ (m3·s);ρ為密度, kg/m3;ν為各相流速,m/s;A為管內過流截面積, m2;ψg為氣液相間質量傳遞速率, kg/(m3·s) ;ψe為液滴夾帶速率,kg/(m3·s) ;ψd為液滴沉積速率, kg/(m3·s) ;下標g、 L、 D 分別表示氣相、 液滴、 液膜。

式中:λ為各相起伏度, m-1;α為管道與豎直方向夾角, (°);p為壓力, Pa;νr為相對速度,m/s;να為沿豎直方向夾角上的速度, m/s;S為各相界面的濕周, m2;g為重力加速度, m/s2; 式中下標i 表示氣液相界面。

式中:E為單位質量流體的內能, J/kg;h為高程,m;H為各相單位質量的焓, J/kg;Hs為質量源的焓, J/s;U為管壁傳熱量, J/s。

通過調整質量流量, 觀察不同流量條件下起伏管道壓降和持液率的變化, 見圖2。

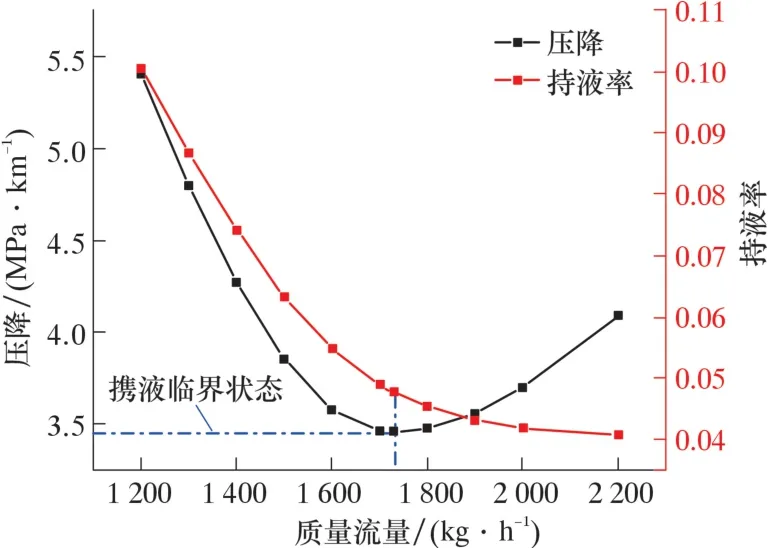
圖2 持液率和壓降隨氣量變化趨勢Fig.2 Liquid holdup and pressure drop vs. gas flow rate

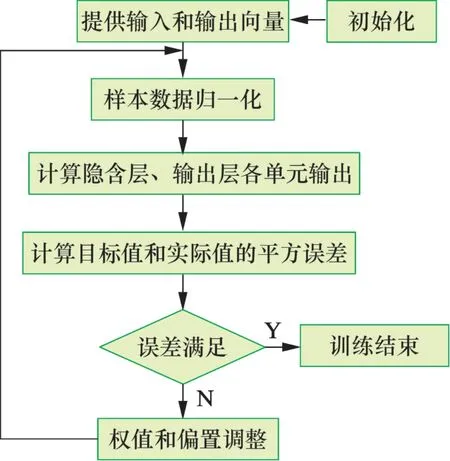
圖3 BP 網絡計算程序框圖Fig.3 Block diagram of the BP neural network computation program

由圖2 可見, 在一定的運行工況下, 隨著氣體流量增加, 上傾管段的平均持液率表現出快速下降后維持在0 附近, 而每千米壓降表現出先下降后上升的非單調變化趨勢。 取最小壓降點為攜液臨界狀態點, 即為攜液臨界流量, 折算至該工況下的表觀天然氣流速即為攜液臨界流速。 由此可知, 起伏管線攜液臨界流速為4.66 m/s。

2 BP 神經網絡預測模型建立

2.1 BP 神經網絡構建

基于最小壓力梯度法, 模擬計算不同工況下起伏管線的攜液臨界流速, 采用 BP 神經網絡對計算數據進行挖潛, 建立攜液臨界流速的預測模型。BP 神經網絡的關鍵參數主要包括網絡層數、 每層神經元數、 神經元的權值與偏置等。 其中, 權值與偏置由訓練得到。 由于3 層BP 神經網絡可以任意精度逼近任意函數, 所以選用單隱層BP 神經網絡對攜液臨界流速進行預測, 其網絡結構包括輸入層、 隱含層和輸出層。 輸入層變量選擇需遵循對輸出層變量影響大、 同時易于檢測或提取的變量, 因此選取管線運行壓力、 井口溫度、 含水體積分數、上下坡傾角及管徑作為輸入層變量, 同時選擇攜液臨界流速作為輸出層變量; 隱含層節點的作用是汲取訓練樣本的內在規律。 最佳隱含層節點數計算公式為:

式中:n為隱含層節點數;ni為輸入節點數;no為輸出節點數;a為1～10 之間的常數。

通過試算比較, 當隱含層節點數為5 時, 預測誤差較小, 因此采用6-5-1 的網絡結構。 BP 神經網絡訓練采用Levenberg-Marquardt 算法, 其訓練函數為trainlm。 對于中等規模的BP 神經網絡, Levenberg-Marquardt 算法具有最快收斂速度, 同時避免了計算Hessian 矩陣, 從而減少了訓練計算量。同時選取TANSIG 正切S 型函數、 PURELIN 線性函數作為輸入層到隱含層、 隱含層到輸出層之間的傳遞函數。 BP 網絡計算的主程序流程圖和結構圖如圖 3 和圖4 所示。數量有效樣本數據, 采用均勻試驗設計結合擴展雙流體分相模型對起伏管路進行水力、 熱力參數計算。 均勻設計參數如表2 所示。

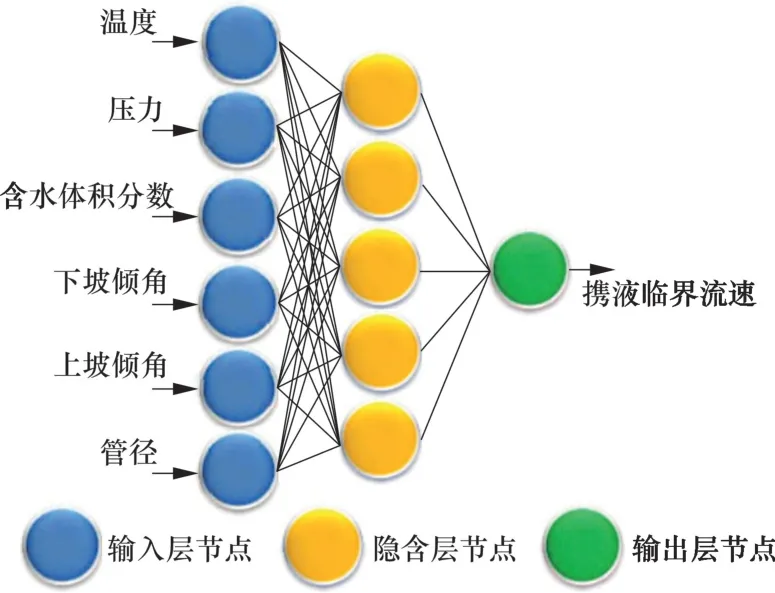
圖4 BP 網絡結構圖Fig.4 BP neural network structure

表2 均勻設計參數Table 2 Parameters of the uniform design for tests

2.2 BP 神經網絡訓練和預測

為了盡可能在輸入層變量取值范圍內獲取最大

基于Y439 井區現場集輸工況, 模擬采集了不同條件下的有效樣本數據80 組, 訓練采用的80 組樣本數據如圖5 所示。

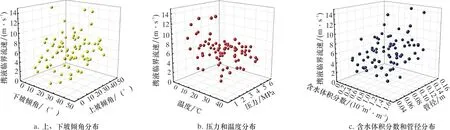
圖5 均勻樣本訓練數據圖Fig.5 Plots of uniform sample training data

同時額外計算采集11 組數據, 分別用來測試模型泛化能力和進行數據預測。 具體數據如表3 和表4 所示。

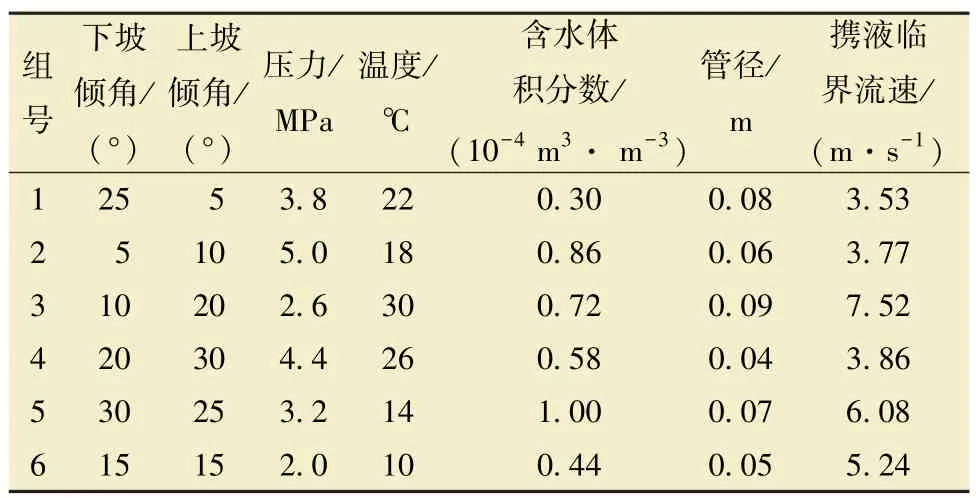
表3 模型泛化能力驗證數據Table 3 Data for the generalization performance validation of the model

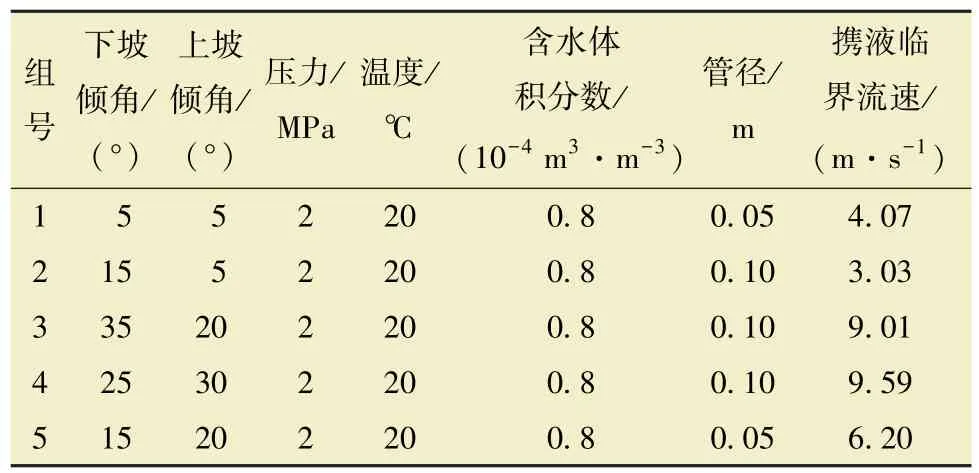
表4 模型預測對比數據Table 4 Data for the model prediction validation

設定BP 神經網絡的學習率為0.04, 訓練要求收斂精度為10-5; 同時為了提高模型的泛化能力防止過度學習, 采用表3 中計算數據對其泛化能力進行驗證(若連續20 次訓練誤差無法降低, 則結束訓練任務)。 模型訓練的誤差曲線和擬合程度見圖6 和圖7。

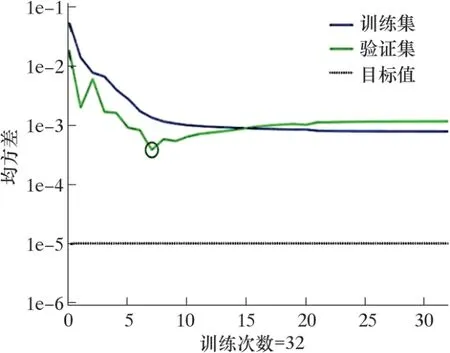
圖6 BP 神經網絡訓練誤差曲線Fig.6 Errors of the training of the BP neural network

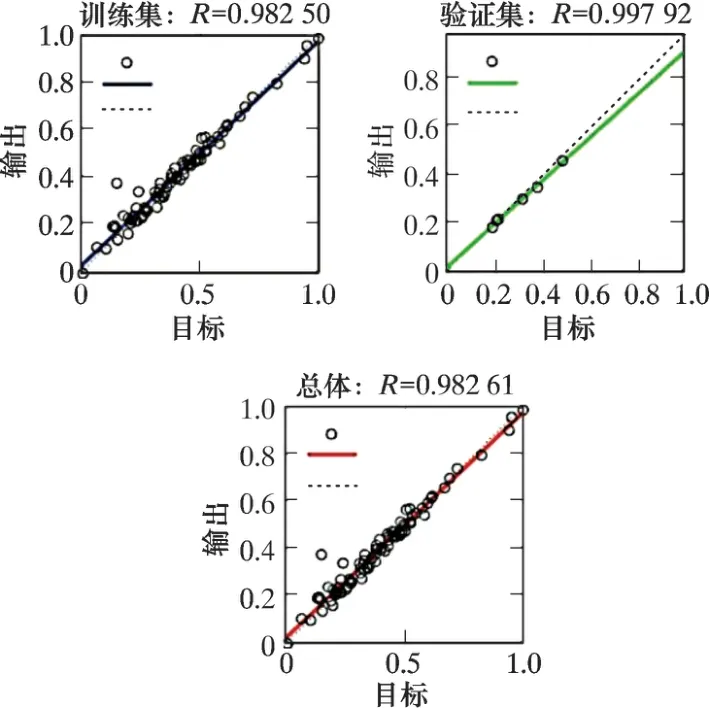
圖7 模型擬合結果Fig.7 Fitting results of the model

由圖6 可知, 在訓練至32 次時, 訓練誤差降至10-3以下, 同時訓練誤差不再降低, 因此訓練結束。 從圖7 可以看到, 模型總體擬合程度較高, 相似系數達到0.982 61, 表明預測模型中期望及預測值存在較高的相關性, 滿足預測要求。

采用表4 中數據, 利用訓練好的預測模型對起伏管路攜液臨界流速進行驗證, 預測結果如圖8 所示。 由圖8 可知, 其最大相對誤差為9.8%, 平均相對誤差為5%, 誤差在多相流管輸工程實踐允許的范圍內, 表明預測模型可以較為準確地預測天然氣攜液臨界流速。

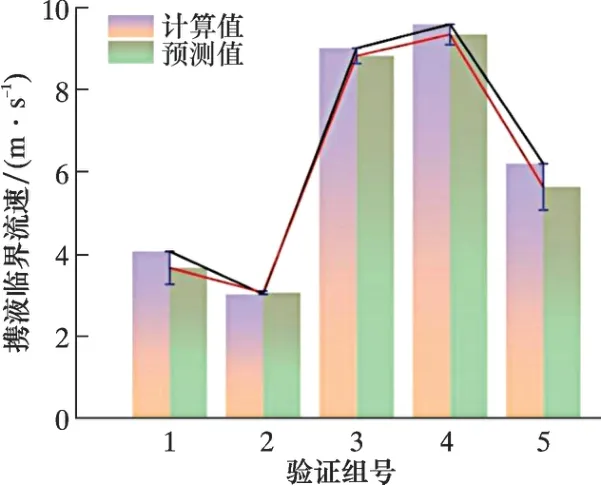
圖8 誤差對比結果Fig.8 Comparison of errors

2.3 模型實例驗證

選取延安氣田Y439 井區內存在積液問題的4條典型輸氣管線, 基于輸氣管網實際運行參數, 采用擴展雙流體分相模型進行模擬計算, 結果如圖9和表5 所示。

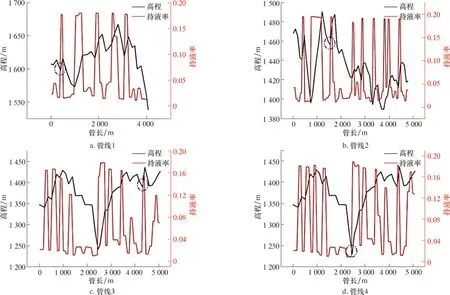
圖9 管線沿線持液率變化曲線Fig.9 Liquid holdup variation along the pipeline

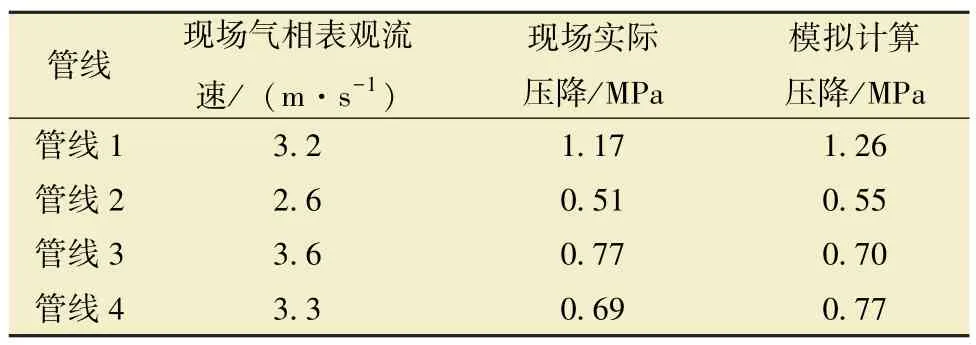
表5 壓降數據對比Table 5 Comparison of pressure drops

由圖9 (藍色圓圈位置為最大上坡傾角所在起伏段) 可知, 管線下坡段氣液分層流動, 沿線持液率基本維持在0 附近; 上坡段沿線持液率迅速提升, 特別是在大上坡傾角區域, 由于氣體攜液能力不足會形成明顯段塞, 造成井口回壓增大, 危及管道安全。 從表5 可以看出, 現場實際壓降與模擬計算壓降變化趨勢非常接近, 平均相對誤差在10%以內, 滿足現場工程要求。 計算結果表明, 上述管線確實存在明顯積液問題, 與實際情況一致。

利用建立的BP 攜液臨界流速預測模型分別計算管線1～4 的攜液臨界流速, 見表6。

表6 預測模型攜液臨界流速計算結果Table 6 Critical liquid-carrying velocity calculated by the model

在攜液臨界流速下, 采用擴展雙流體分相模型對管線1～4 的運行工況進行模擬, 結果如圖10 所示。

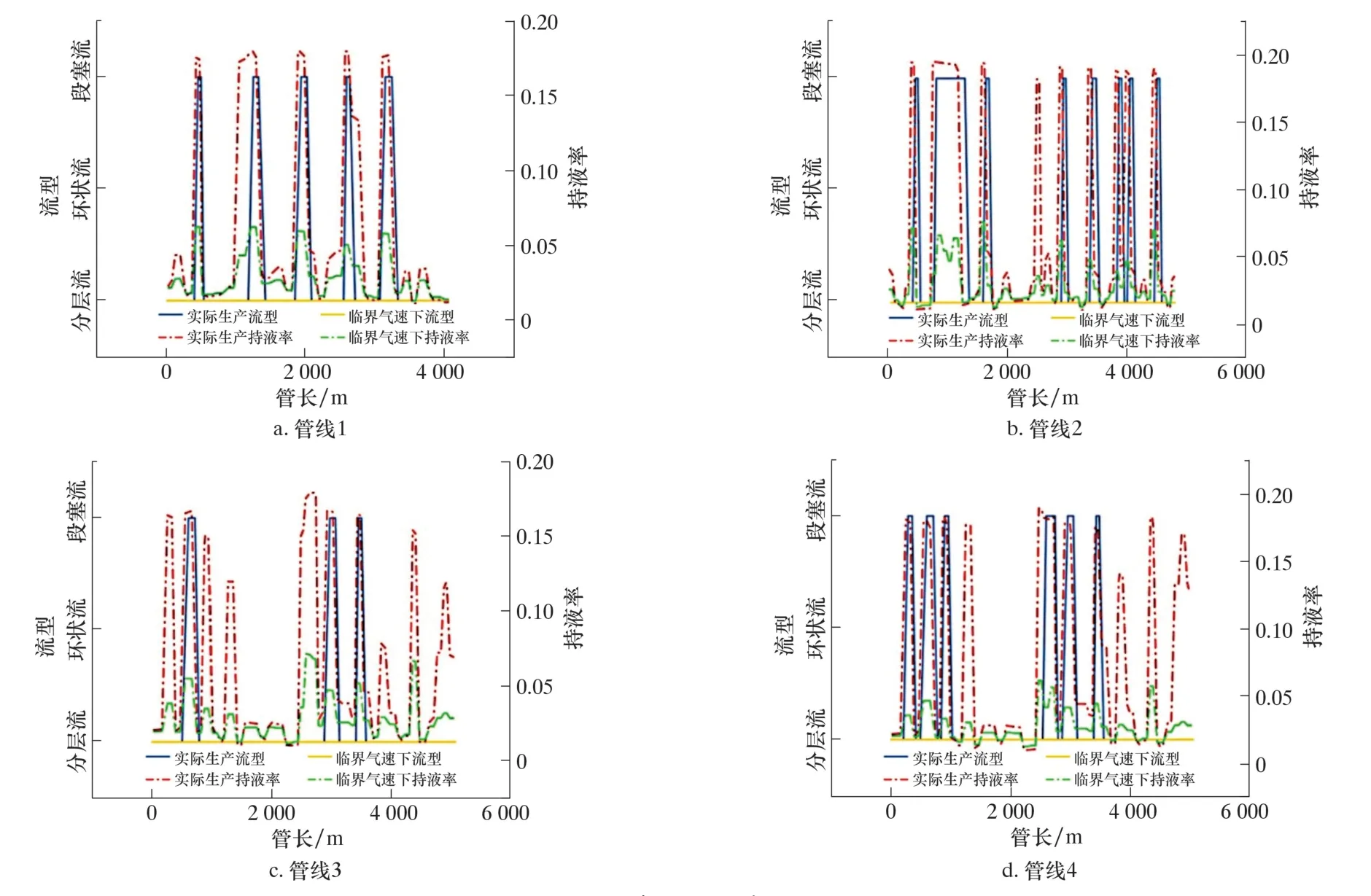
圖10 攜液臨界流速下管線沿線持液率、 流型變化曲線Fig.10 Variations of liquid holdup and flow regime along the pipeline at the critical liquid-carrying velocity

從圖10 可以發現: 管線沿線持液率均大幅下降, 在氣田實際生產中持液率較高的區域多為段塞流; 當氣體流速達到攜液臨界流速后, 沿線流型轉換為分層流, 此時液膜平鋪在上傾管段, 管線壓降顯著降低。 模擬結果表明, 該預測模型得到的攜液臨界流速具有合理性, 可以指導生產實踐。

3 因素回歸分析

利用建立的BP 攜液臨界流速預測模型對影響其攜液能力的各因素變化規律進行回歸分析。

3.1 井口溫度和運行壓力

選擇管徑80 mm, 上坡傾角15°, 下坡傾角15°, 含水為0.6 m3/(104m3) , 井口溫度2 ～38℃, 運行壓力1.5 ～5.5 MPa, 分析井口溫度和運行壓力變化對攜液臨界流速的影響, 結果如圖11和圖12 所示。

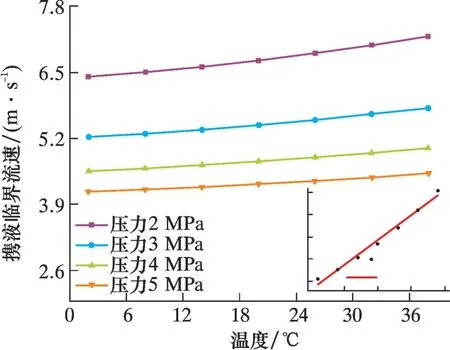
圖11 不同井口溫度下攜液臨界流速隨運行壓力變化曲線Fig.11 Critical liquid-carrying velocity vs. pipeline operation pressure at different wellhead temperatures

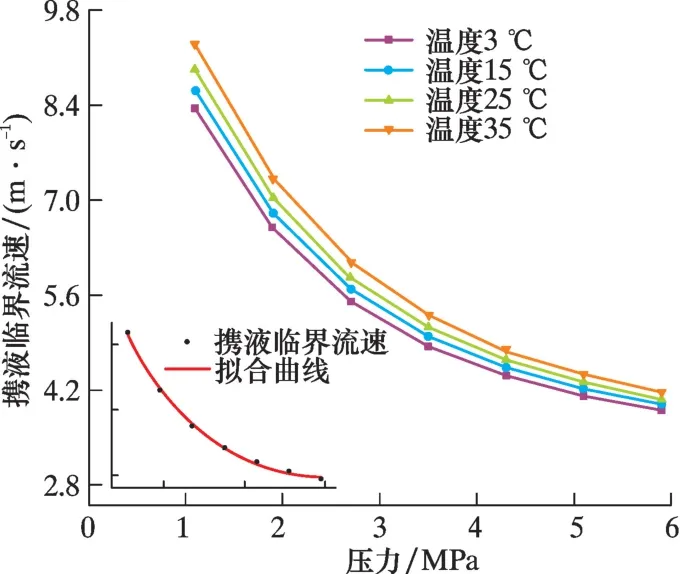
圖12 不同運行壓力下攜液臨界流速隨井口溫度變化曲線Fig.12 Critical liquid-carrying velocity vs. wellhead temperature at different operation pressure

井口溫度和運行壓力對攜液臨界流速的影響主要在于氣體的密度和動力黏度。 伴隨井口溫度升高, 氣體密度降低, 動力黏度增大, 氣液相間剪切應力略有減小; 攜液臨界流速相應增高, 但增幅有限, 其變化規律近似呈線性關系。 隨著運行壓力提高, 依據氣體PVT 狀態方程, 氣體密度增大, 動力黏度增大, 液膜受到的剪切應力相應增大, 氣體攜液能量增強, 穩定運移單位長度液膜所需的氣體流量降低, 即攜液臨界流速降低, 且降低速度逐漸變緩, 近似呈指數變化趨勢。

3.2 含水體積分數

選擇管徑80 mm, 運行壓力5 MPa, 井口溫度20 ℃, 下坡傾角15°, 上坡傾角10°～40°, 含水體積分數0.12～1.44 m3/(104m3) , 分析不同上坡傾角下含水體積分數變化對攜液臨界流速的影響, 結果如圖13 所示。

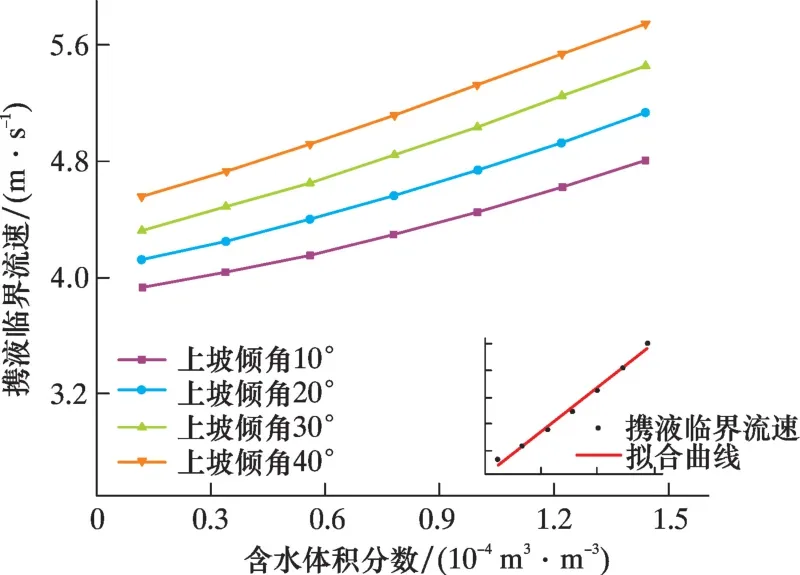
圖13 不同上坡傾角下攜液臨界流速隨含水體積分數變化曲線Fig.13 Critical liquid-carrying velocity vs. water content with different up-slope angles

由圖13 可知, 隨著氣體含水體積分數增加,液相表觀流速逐漸增高, 管內液膜厚度增加, 維持液膜沿上傾管線穩定運移且不發生反轉的氣量逐漸提高, 即攜液臨界流速增大, 且變化規律近似呈線性關系。 這也與Wallis 模型中液相影響項變化趨勢一致。

3.3 爬坡傾角

選擇管徑50～140 mm, 運行壓力5 MPa, 井口溫度20 ℃, 含水體積分數0.6 m3/(104m3) , 管線上下坡傾角1.5°～44.9°, 分析不同管徑下爬坡傾角變化對攜液臨界流速的影響, 結果如圖14 和圖15 所示。

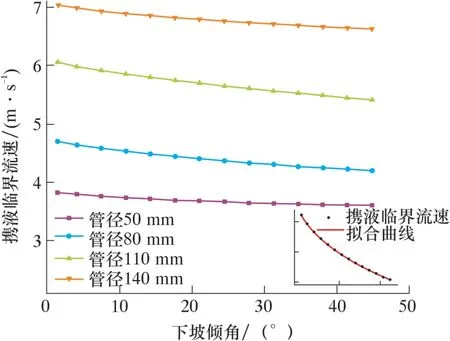
圖14 不同管徑下攜液臨界流速隨下坡傾角變化曲線Fig.14 Critical liquid-carrying velocity vs. down-slope angle with different pipe diameters

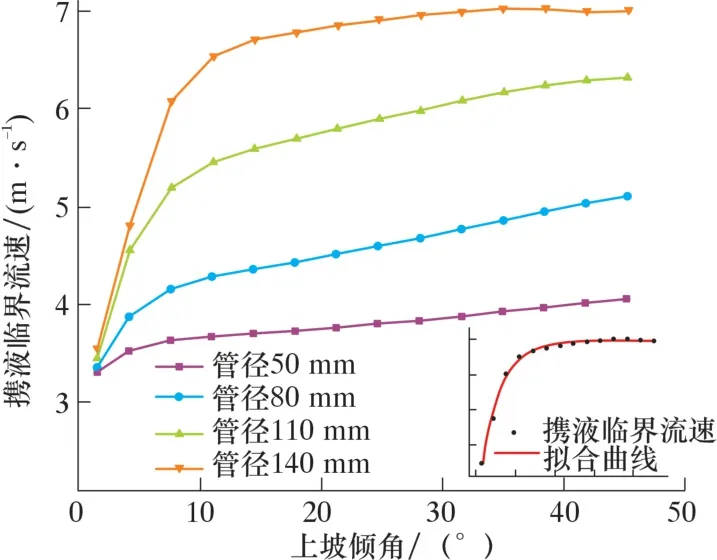
圖15 不同管徑下攜液臨界流速隨上坡傾角變化曲線Fig.15 Critical liquid-carrying velocity vs. up-slope angle with different pipe diameters

由圖14 可知, 隨著下坡傾角增大, 液膜在管道軸線方向重力分量作用下液相濕周增大, 液膜沿管內壁周向分布逐漸均勻, 單位長度液膜厚度減薄; 氣體攜液臨界流速降低, 但降低幅度有限, 變化趨勢近似呈現指數關系。 由圖15 可知, 隨著上坡傾角增大, 液膜在管道軸線方向的重力分量不斷增加, 氣體攜液所需的能量逐漸提高; 同時隨著上坡傾角增大, 液膜沿管道內壁周向分布均勻, 管道內壁周向底部液膜減薄, 液膜所受重力分量與液膜

分布情況同時發生改變, 造成攜液臨界攜流速先迅速提高后逐漸放緩, 近似呈現對數變化趨勢。

3.4 管徑

選擇運行壓力5 MPa, 井口溫度20 ℃, 含水體積分數0.6 m3/(104m3) , 管線下坡傾角15°,上坡傾角15°～30°, 管徑45～145 mm, 分析不同上坡傾角下管徑對攜液臨界流速的影響, 見圖16。由圖16 可知, 隨著管徑增大, 管道內氣液流通面積提高, 氣液相間剪切作用降低, 氣體對液膜的曳力減小; 攜液臨界流速逐漸增大, 其變化近似呈線性關系。

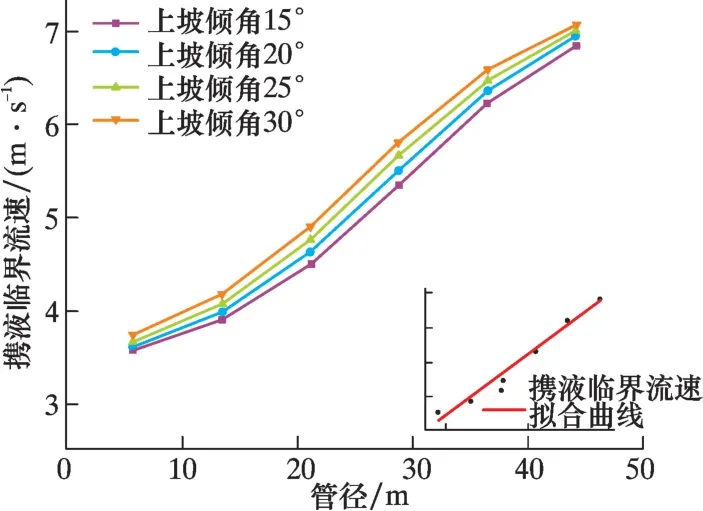
圖16 不同上坡傾角下攜液臨界流速隨管徑變化曲線Fig.16 Critical liquid-carrying velocity vs. pipe diameter with different up-slope angles

3.5 交互作用分析

為了進一步分析井口溫度、 運行壓力、 含水體積分數、 上下坡傾角、 管徑6 種因素的交互作用對氣體攜液臨界流速的影響規律, 基于BP 攜液臨界流速預測模型, 繪制了因素兩兩交互作用的二維等高線云圖, 如圖17 所示。

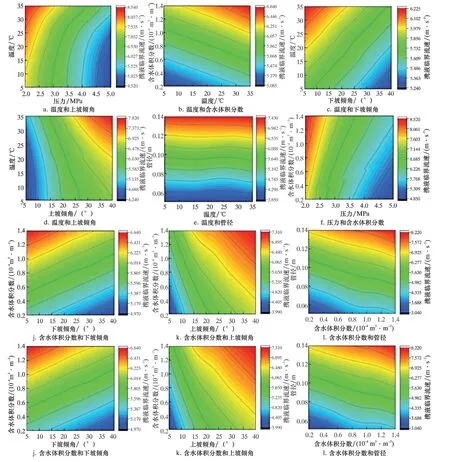
圖17 攜液影響因素交互作用云圖Fig.17 Contours of interaction among factors affecting liquid-carrying

由圖17a 和圖17c 可以看出, 井口溫度與運行壓力和下坡傾角存在相反作用影響, 當井口溫度降低且運行壓力和下坡傾角升高時, 攜液臨界流速到達最低, 單純降低井口溫度對降低攜液臨界流速效果有限; 由圖17b、 圖17d 可知, 井口溫度與含水體積分數和上坡傾角存在一定程度的協同作用影響, 但當上坡傾角較小時, 攜液臨界流速隨井口溫度變化不是很明顯; 由圖17e 可知, 相對井口溫度的變化, 管徑對攜液臨界流速的影響占據主導地位; 圖17f、 圖17h 和圖17i 表明, 運行壓力與含水體積分數、 上坡傾角和管徑呈現相反作用影響,當運行壓力提高且含水體積分數、 上坡傾角和管徑降低時, 攜液臨界流速達到最低, 但當運行壓力較低時, 含液體積分數對攜液臨界流速的影響幅度有限; 圖17g 表明下坡傾角相較運行壓力而言, 對攜液臨界流速的影響有限特別是在高壓狀態時; 從圖17j、 圖17k 和圖17i 可知, 含水體積分數與下坡傾角呈相反作用影響, 與上坡傾角和管徑具有協同作用影響; 圖17m 表明, 當下坡傾角最大而上坡傾角最小時攜液臨界流速達到最低, 但下坡傾角變化的影響幅度有限; 從圖17n 和圖17o 可以看到, 相較上下坡傾角的變化, 管徑對攜液臨界流速的影響占據主導地位。

3.6 攜液因素敏感性分析

為了探究各影響因素對攜液臨界流速的影響程度, 利用均勻設計的模擬計算結果, 采用灰色關聯進行分析。 建立原始數據子序列2, …,m;t= 1, 2, …,N。 其中,m代表序列中的元素, 表示影響因素數量(m=6);N代表每個序列的長度, 表示試驗組數(N=80); 原始數據母序列為代表各組試驗對應的攜液臨界流速。

將原始數據序列進行均值化變換, 計算式為:

利用均值化變換后的數據序列, 計算母序列{X0(t)}與子序列{Xw(t)}的相關系數Lw(t), 計算式為:

式中:Δw(t) 為母序列與子序列之間的絕對差值;Δmin和Δmax是所有絕對差值中的最大值和最小值,Δmin=0.000 22,Δmax=2.084 57;s為分辨系數, 取0.1。

將Lw(t) 數據序列進行算數平均, 計算式為:

式中:r0w為母序列與子序列之間的相關系數, 計算值如表7 所示。

表7 相關系數計算結果Table 7 Calculated correlation coefficients

從計算結果可以看出, 影響地面起伏管線臨界攜液流速的各因素重要性排序為: 管徑＞上坡傾角＞含水體積分數＞運行壓力＞下坡傾角＞井口溫度。

4 結 論

(1) 攜液臨界流速隨井口溫度、 含水體積分數以及管徑近似呈線性變化, 隨上坡傾角近似呈對數變化, 隨運行壓力和下坡傾角近似呈指數變化,且各因素間交互作用明顯。

(2) 利用灰色關聯分析了影響管線攜液臨界流速的主要因素, 并對其重要性進行排序, 結果表明, 管徑影響最大, 其次為上坡傾角、 含水體積分數和運行壓力, 其他因素的敏感性差距相對較小。

(3) 基于最小壓力梯度法, 采用擴展雙流體分相模型結合均勻設計和BP 神經網絡, 建立了一種起伏管線攜液臨界流速的預測模型, 同時采用延安氣田Y439 井區集輸現場數據對模型進行了驗證。 驗證結果表明, 在攜液臨界流速下, 管線沿線持液率大幅降低, 正常生產工況下積液嚴重區域的流型由段塞轉變為分層, 證明模型預測效果良好,同時對延安氣田多起伏地面管線具有較強適用性。