脫插機構的誤差靈敏度分析與優化設計

孫繼紅，武令偉，陳冰

(1.海軍裝備部武漢局駐鄭州地區軍事代表室，河南 鄭州 450015；2.中國船舶集團有限公司第七一三研究所，河南 鄭州 450015)

0 引言

精密機械系統在裝配組裝過程中，零件的加工誤差和裝配誤差不斷累積，勢必會影響精密機械系統的性能指標。如何系統量化分析零部件的加工誤差與裝配誤差對整個多體系統的精度影響，對整個系統的可靠性起著關鍵作用[1]。針對該問題，國內外學者進行了大量研究。呂程等[2]以裝配結合平面為研究對象，分析了多種公差耦合情況下零件間裝配結合面誤差建模和公差優化設計問題。楊強等[3]應用差分法分析了并聯機構位置誤差對主要設計變量的靈敏度的影響。趙強等[4]用矩陣微分法推導了位姿誤差和原始誤差之間的關系式，給出了按靈敏度的比例對原始誤差進行綜合優化的方法。唐水龍等[5]針對配合面尺寸公差與平面度公差構建虛擬配合面進行了誤差耦合分析。范晉偉等[6]提出了一種基于多體系統運動學理論的機床誤差靈敏度分析新方法，提出了矩陣微分法的靈敏度分析模型。

雷彈發射箱脫插機構是雷彈貯運發射箱的重要組成部分，完成發控專用電纜與箱、雷之間的連接與導通，用于雷彈和反潛武器系統之間信號傳輸，并在雷彈發射時，確保雷箱之間的電連接器可靠快速地自動分離，為雷彈正常出箱提供發射通道，是保證雷彈正常發射的重要組件。由于脫插機構既要保證發射箱與雷之間精準對接和發射時可靠快速的自動分離，又不干涉到正在出箱的雷彈，因此對脫插機構與雷彈之間的相對位置精度要求極高，對脫插機構各零部件的加工精度以及裝配精度提出了較高的要求。本文以某型雷彈貯運發射箱脫插機構為研究對象，建立脫插機構多體系統的誤差傳遞模型，并對影響其精度的因素進行靈敏度分析，進而確定關鍵誤差來源，為整個系統的誤差優化分析提供可靠的理論支撐。

1 多體系統幾何誤差傳遞模型

1.1 誤差描述

任何多體系統都由若干個零件裝配而成，組成多體系統的零部件在加工和裝配的過程中不可避免都存在一定的誤差。整個多體系統隨著一個個零件的裝配，零件本身的加工誤差和裝配過程中產生的裝配誤差，將會出現誤差不斷疊加和增大現象，進而對整個多體系統的工作性能產生較大影響，因此控制多體系統幾何誤差疊加對多體系統性能起著至關重要的作用。

為了便于分析多體系統的幾何誤差疊加，需要建立多體系統的幾何誤差傳遞模型，通常將零件的加工誤差和裝配誤差用向量[?α ?β ?γ ?x?y?z]表示，其中 ?x，?y，?z表示在右手直角坐標系Oxyz各方向上的線位移誤差，?α，?β，?γ表示角位移誤差[7]。

現將兩個相互配合的零件設為A 和B，分別在其相互配合的理想幾何表面中心建立右手坐標系，oxAyAzA和oxByBzB，相對于理想幾何表面的實際幾何表面建立坐標系分別為oxA′yA′zA′’和oxB′yB′zB′[8–9]。

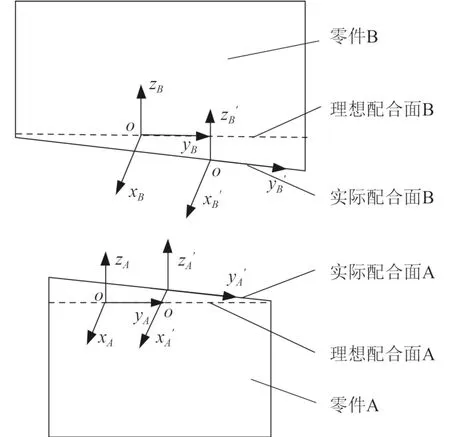
圖1 配合面誤差專遞模型Fig.1 Matching surface error transformation model

其中坐標系oxA′yA′zA′相對于oxAyAzA，存在3 個角位移誤差?α，?β，?γ和3 個線位移誤差 ?x，?y，?z。2 個坐標系的齊次變換矩陣為：

由于精密系統的各個誤差數值很小，令式（1）中cos?α ≈1，cos?β ≈1，cos?γ ≈1，sin?α ≈?α，sin?β ≈?β，sin?γ ≈?γ，同時忽略高階小量，則齊次變換矩陣可表示為：

坐標系oxAyAzA中的向量a=[ax ay az1]T在坐標系oxA′yA′zA′可表示為：

為了便于區分不同零件間的變換矩陣，令

同理可得，oxByBzB相對于oxB′yB′zB′齊次變換矩陣為TB，oxAyAzA相對于oxByBzB齊次變換矩陣為oxA′yA′zA′相對于oxB′yB′zB′齊次變換矩陣為根據坐標變換關系，并且忽略高階小量，可得理想面A相對于理想面B 的坐標變換矩陣為：

坐標系oxByBzB上的向量pb在坐標系oxAyAzA中可表示為：

1.2 脫插機構多體系統坐標系定義和變換

發射箱脫插機構的多體系統簡化結構如圖2 所示。脫插機構與雷彈對接時，只有脫插機構內部機構在運動，因此在進行誤差分析時，可將脫插機構基座與發射箱考慮為一個整體，并在脫插機構基座上建立以雷彈發射方向為x軸，以脫插機構對接方向為z軸建立基本坐標系o?xyz，將脫插機構下連桿座定義為剛體1；脫插機構平動桿視為剛體2；脫插機構上連桿座視為剛體3；電插頭視為剛體4，可以建立脫插機構對應的多體系統拓圖如圖3 所示。

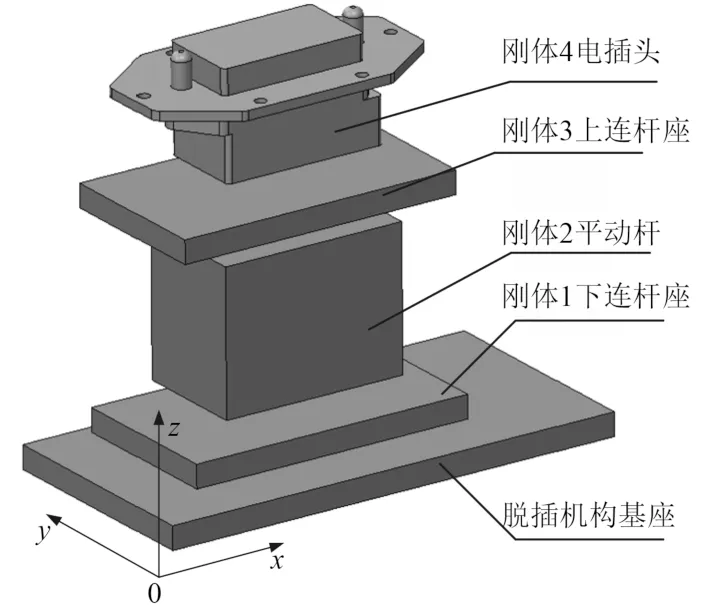
圖2 發射箱脫插機構結構簡化圖Fig.2 Simplified structure diagram of launch canister insert-draw

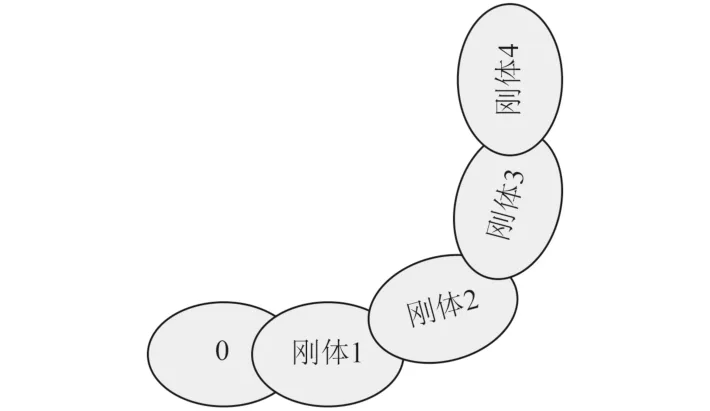
圖3 發射箱脫插機構拓撲圖Fig.3 Topological diagram of launch canister insert-draw

因此，剛體4中的任意一向量m4=[mx my mz1]T在基本坐標系o?xyz中可表示為：

假設整個脫插機構各個配合面之間不存在加工誤差和裝配誤差，則向量m4在基本坐標系o?xyz中可表示為：

向量m4的總體誤差矢量可以表示為：

1.3 脫插機構靈敏度分析模型

假設X為脫插機構裝配后的總體誤差矢量，?xX，?yX，?zX，?αX，?βX，?γX分別為函數X的6 個誤差分量，因此可得

其中，X為系統的空間誤差矢量，Uk為誤差矢量。

根據一階靈敏度函數的定義，假設函數F(x)可導，則F(x)的一階靈敏度可表示為：

由脫插機構誤差傳遞模型可知，X是Uk各個誤差變量的連續可微函數，因此可得脫插機構的誤差靈敏度分析模型為：

式中：Ek=?f/?Uk為對應變量的靈敏度系數，因此，可以計算求出每一個誤差分量對系統總裝誤差的靈敏度系數，即Ek=?f/?Uk為誤差靈敏度系數矩陣：

根據式（11）可以快速的計算各誤差的靈敏度系數。同時為了快速的找到關鍵誤差，對各個靈敏系數，進行了歸一化處理可得[10]：

式中：Ck代表誤差Uk各誤差分量的靈敏度系數，而全部靈敏度系數之和為1。

2 脫插機構總體誤差分析

2.1 誤差矢量計算

首先，測量脫插機構各關鍵零部件配合面的多個點尺寸，經計算擬合分析，再通過式（4）計算得出各配合面的相對誤差矢量如表1 所示。

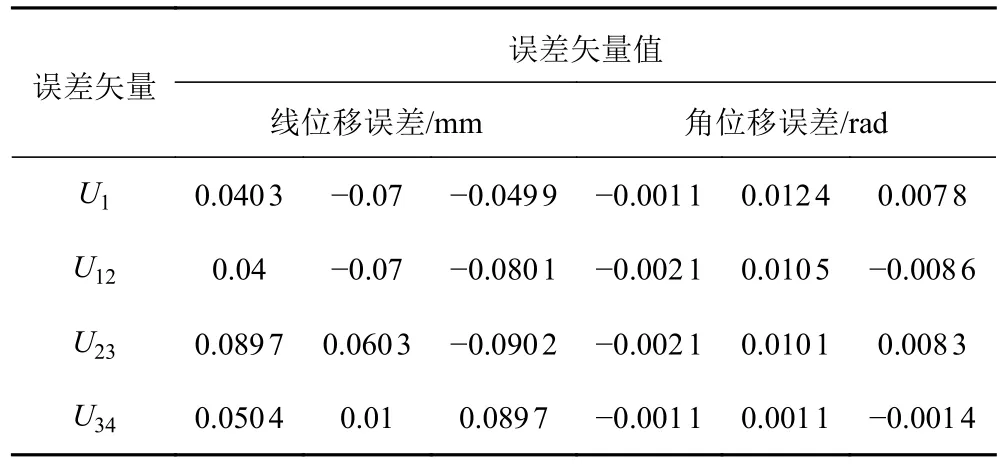
表1 各配合面的相對誤差矢量Tab.1 Relative error vector of each mating surface

將表1 中的數據代入式（8）和式（9），經計算可得脫插機構總體相對誤差矢量如表2 所示。

表2 脫插機構總體相對誤差矢量Tab.2 Overall relative error vector of insert-draw

表2 中脫插機構總體相對誤差矢量在3 個方向的線位移誤差分別為：1.920 8 mm，05041 mm 和?0.756 8 mm，3 個方向的角位移誤差分別為：?0.0065，0.0341 和0.0062。

通過對脫插機構多個對接失敗的案例進行統計分析發現，造成脫插機構對接失敗的主要因素為脫插機構的電插頭，在z軸方向和x軸方向上誤差過大。當誤差為正時，會使電插頭上升到最高位置尚不能完全插入雷彈電插座中；當誤差過小時會使電插頭還沒有旋轉至豎直對接位置時，電插頭的導向銷已和雷彈上電插座干涉，以致因插座的阻擋不能繼續執行對接操作，導致對接失敗。因此，為了減少計算量主要關注誤差分量在x軸、y軸和z軸方向上的靈敏度系數。根據式（15）求得脫插機構各誤差分量分別在x、y、z方向上靈敏度系數，并根據式（16）進行歸一化處理，并取靈敏度系數最大的3 項，可得表3。

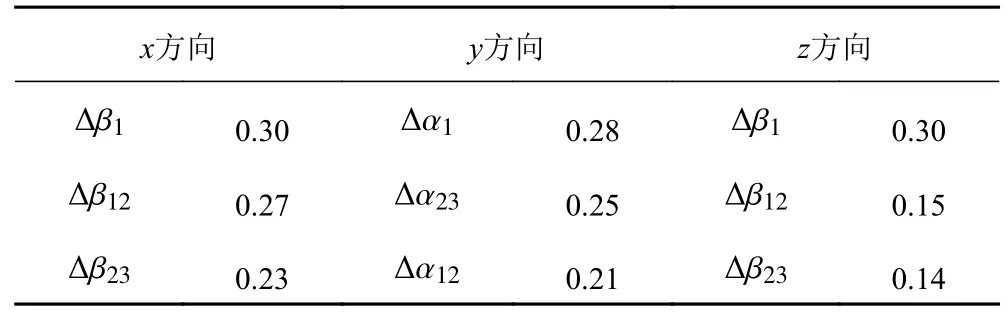
表3 各誤差分量在x，y，z 軸方向上的誤差靈敏度系數Tab.3 Error sensitivity coefficient of each error component in x,y and z axes

2.2 關鍵因素確定

考慮脫插機構對接失敗的主要原因可能來自于x軸方向和z軸方向的誤差，根據表3 中的各誤差靈敏度系數可知，影響脫插機構x軸方向和z軸方向的誤差的主要影響因素為?β1，?β12和?β23，即將脫插機構下連桿座和脫插機構基座之間沿y軸方向的轉動誤差；下連桿座和平動桿之間沿y軸方向的轉動誤差；平動桿和上連桿座之間沿y軸方向的轉動誤差。因此考慮針對上述3 項誤差提出改進方案，進而提高脫插機構的對接成功率。

3 措施制定及試驗驗證

3.1 措施制定

針對計算分析的結果，根據分析出的原因，通過提高脫插機構下連桿座和脫插機構基座之間、下連桿座和平動桿之間、平動桿和上連桿座之間配合面沿x軸方向的平面度要求（即降低沿y軸方向的轉動誤差）以及裝配間隙的均勻性，進而降低?β1，?β12和?β23的數值從而降低x軸方向和z軸方向的誤差，將? β1，?β12和?β23進行調整，如表4 所示。對脫差機構各配合面優化后，計算系統整體誤差矢量，同時測量實際誤差并與優化前的誤差矢量進行對比，如表5 所示。

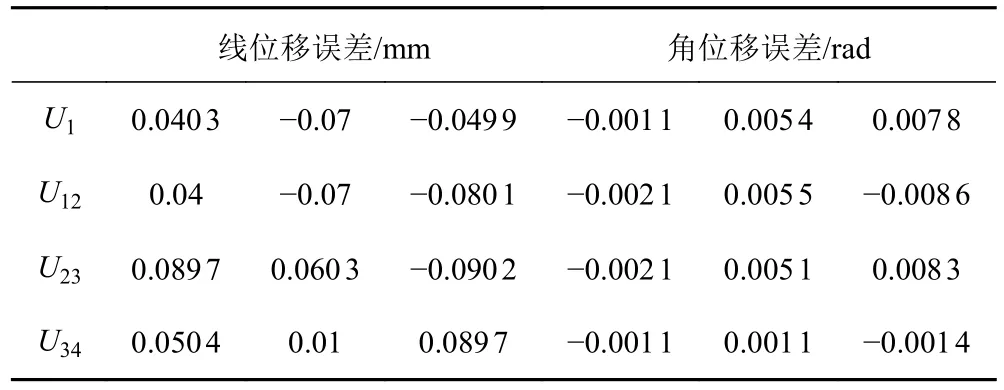
表4 優化后各配合面的相對誤差矢量Tab.4 The relative error vector of each mating surface after optimization

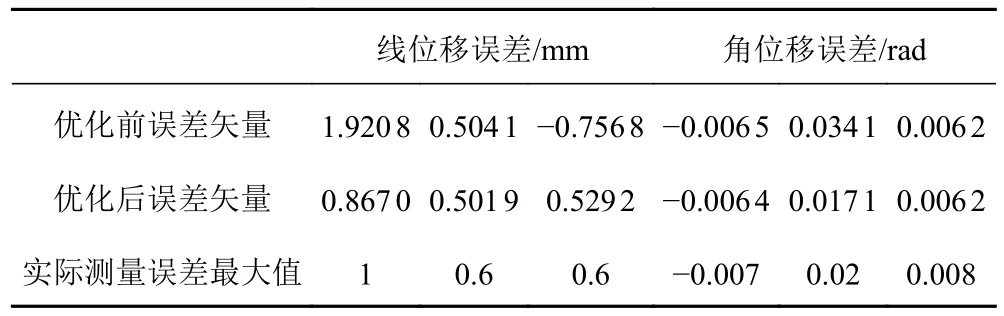
表5 優化前后脫插機構總體相對誤差矢量Tab.5 Optimize the overall relative error vector of the front and rear insert-draw

3.2 試驗驗證

在試驗現場，將優化設計并檢驗合格后的脫插機構安裝到發射箱中，將模擬雷彈推入發射箱中，用固彈機構鎖定。操作脫插機構，使平動桿帶動電插頭到待插狀態，測量電插頭前導向銷中心到雷上插座導向孔中心在z軸方向上的偏差為0.5 mm，沿x軸方向上的偏差為0.8 mm，沿y軸方向上的偏差為0.5 mm，如圖4 所示。

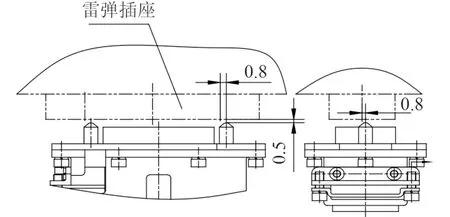
圖4 發射箱上電插頭和雷彈插座相對位置示意圖Fig.4 Schematic diagram of relative position of electric plug and torpedo-missile on launch canister

操作脫插機構使電插頭升起，成功插入雷體插座中。用萬用表對發射箱箱壁外側的插座和模擬雷上插座的導通情況進行檢測，所有芯線均導通正常。操作固彈機構解鎖模擬雷后，用手推動模擬雷向前運動，脫插機構電插頭和雷上插座成功分離，并被脫插機構內鎖定-解鎖機構鎖定。重復操作以上步驟100 次，其中，100 次插接功能都順利完成，在對接成功的100 次操作中隨機抽取幾根芯線檢測，也均導通正常。對接成功率為100%，對比優化前85%的成功率有了較大提高，進一步驗證了措施的有效性。

4 結語

針對發射箱脫插機構與雷彈對接成功率較低容易失敗的問題，本文通過建立發射箱脫插機構的誤差傳遞模型，對脫插機構進行靈敏度分析，確定影響脫插機構對接精度的關鍵誤差來源，為整個系統的誤差優化分析提供理論支撐，從而提出針對性的改進措施并加以實施。最后通過試驗驗證了誤差分析的有效性以及改進措施的正確性，最終解決了脫插機構對接成功率低的問題。