多壓力角雙接觸特殊齒輪精確三維建模研究

黎超 劉祥環 胡曉嵐 謝立湘 袁仲謀 陳勇智

摘要：基于多壓力角雙接觸特殊齒輪的設計理論及加工工藝，提出了一種多壓力角雙接觸特殊齒輪產品的三維建模方法。該方法利用數學工具軟件對齒面進行高精度計算，得到齒面坐標點，利用三維軟件對坐標點進行擬合，形成高精度三維齒面，通過對比理論計算結果與三維建模結果，使其精度滿足有限元分析要求，對于多壓力角雙接觸齒輪的強度計算、NVH仿真分析及產業化制造有極其重要的作用。

關鍵詞：多壓力角雙接觸特殊齒輪齒面方程；齒面點云計算；三維建模

齒輪傳動具備傳遞效率高、傳動平穩、結構緊湊、傳遞轉矩及速度范圍廣等優點，廣泛應用于汽車、工程機械、農業機械及軍工產品等領域，是目前應用最廣泛的一種機械傳動形式[1]。齒輪嚙合過程中，因為輪齒的剛度隨著嚙合線總長度的變化而變化，會存在周期性波動，產生不可避免的傳遞誤差，從而使得傳動系統存在無法避免的振動和噪聲，尤其在乘用車傳動領域，傳動系統的NVH問題已經成為業內的關注重點[2]。同時，斜齒輪在外載荷作用下產生彎扭組合變形，導致載荷沿接觸線分布不均勻，產生偏載現象[3-6]。雖然對齒面進行微觀修形能夠在一定程度上改善這種現象，但是齒面修形對齒輪的制造精度要求極高，直接影響齒輪產品的制造成本和生產效率。株洲齒輪有限責任公司已經將多壓力角雙接觸齒輪產品在電動汽車領域應用，并取得了較好的應用效果[7]，且目前從產品設計、刀具設計、制造工藝到產品檢測全流程技術難題都已攻克。要提高多壓力角雙接觸齒輪的設計、仿真分析、生產效率，實現批量應用，就需要推導出齒面的方程并以此來建立精確的三維模型，利用有限元分析技術來模擬齒輪嚙合過程，來指導產品的設計和制造工作。

多壓力角雙接觸齒面方程

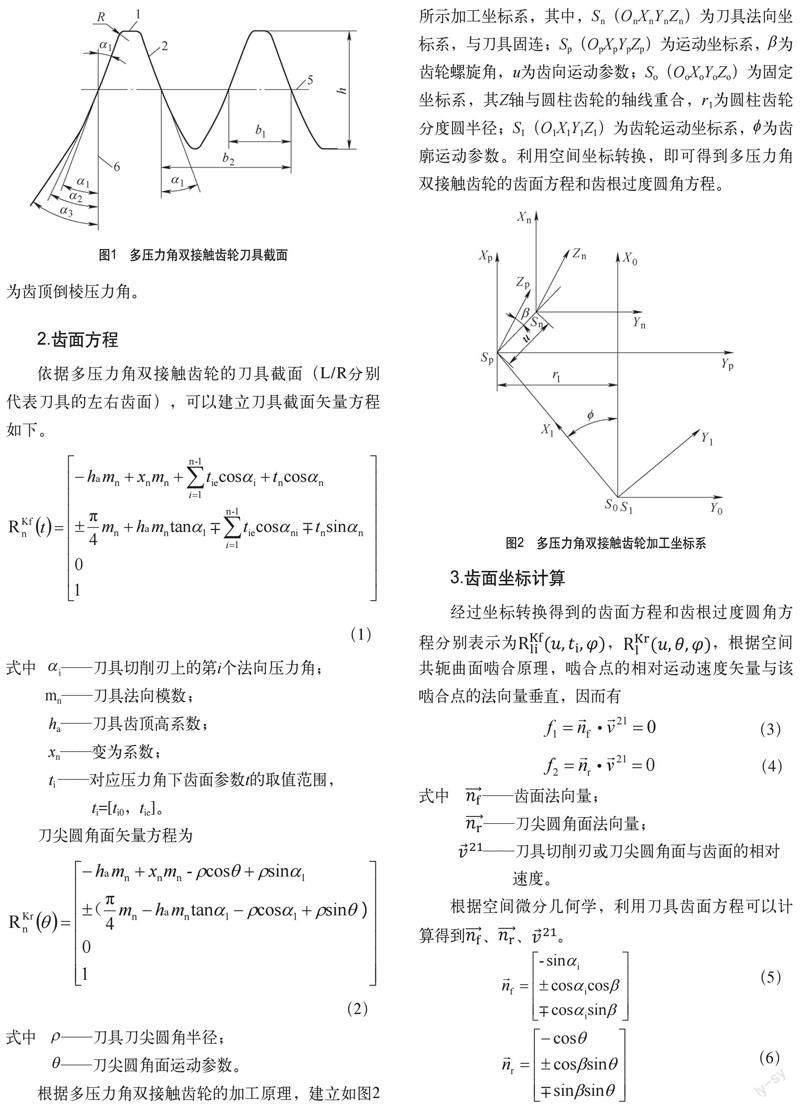
1.刀具截面形狀

多壓力角雙接觸齒輪對的刀具截面[8]形狀如圖1所示。該刀具截面可以根據需求，設計出更多的壓力角，其中α1為標準壓力角，α2為剪除干涉量壓力角，α3為齒頂倒棱壓力角。

2.齒面方程

依據多壓力角雙接觸齒輪的刀具截面（L/R分別代表刀具的左右齒面），可以建立刀具截面矢量方程如下。

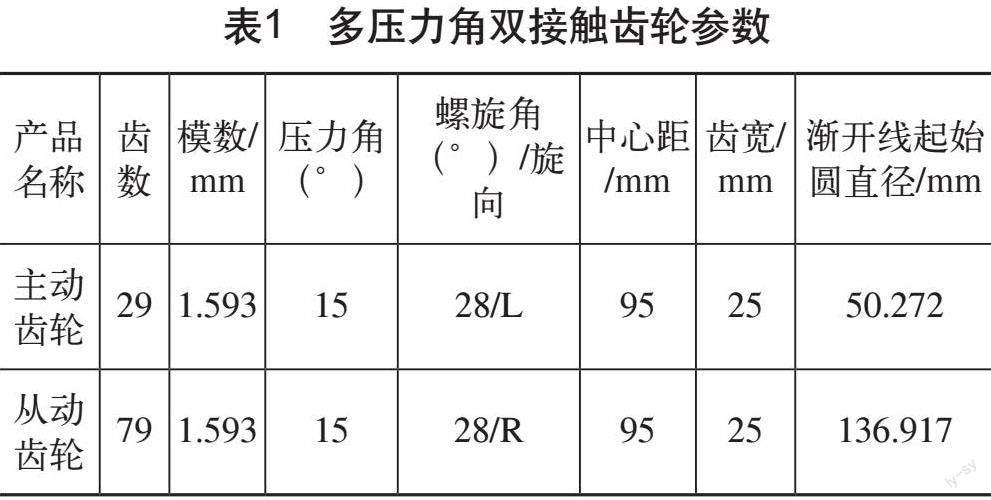
根據多壓力角雙接觸齒輪的加工原理，建立如圖2所示加工坐標系，其中，Sn（OnXnYnZn）為刀具法向坐標系，與刀具固連；Sp（OpXpYpZp）為運動坐標系，β為齒輪螺旋角，u為齒向運動參數；So（OoXoYoZo）為固定坐標系，其Z軸與圓柱齒輪的軸線重合，r1為圓柱齒輪分度圓半徑；S1（O1X1Y1Z1）為齒輪運動坐標系，φ為齒廓運動參數。利用空間坐標轉換，即可得到多壓力角雙接觸齒輪的齒面方程和齒根過度圓角方程。

3.齒面坐標計算

經過坐標轉換得到的齒面方程和齒根過度圓角方程分別表示為，，根據空間共軛曲面嚙合原理，嚙合點的相對運動速度矢量與該嚙合點的法向量垂直，因而有

編寫計算機求解程序文件，計算式（8）和式（9），并控制好齒面邊界條件，即可得到多壓力角雙接觸齒輪的齒面點云數據，從而利用三維軟件擬合齒輪的精確三維模型。

三維建模

根據表1中的齒輪設計基本參數和各壓力角的值，計算出運動參數ti、u、θ的邊界值，分別代入式（8）和式（9）中進行非線性方程求解，即可得到多壓力角雙接觸齒輪的齒面點云數據，將點云數據導入到CREO軟件中進行擬合，可得到如圖3所示的齒面曲線，利用軟件的曲面擬合和布爾運算，可得到多壓力角雙接觸齒輪的三維幾何模型如圖4所示。

根據自主開發的多壓力角雙接觸齒輪計算軟件計算出齒輪參數結果，對比模型齒面關鍵點的幾何尺寸，證實了該建模方法的準確性，模型精度達到有限元分析標準。

結語

1）據多壓力角雙接觸齒輪的設計及加工原理[9-11]，推導出該齒制齒輪副的齒面及齒根圓角面方程。

2）通過求解三元非線性方程組，計算出齒面點云數據，并利用三維設計軟件CREO進行點云數據擬合，從而建立精確的多壓力角雙接觸齒輪三維模型。

3）通過三維建模數據和理論計算數據對比，該模型精度已達到齒輪副有限元分析要求，下一步將對多壓力角雙接觸齒輪副進行有限元網格處理并進行有限元分析。

4）該齒制齒輪副有著高強度、低溫升、低沖擊噪聲等優點，已經小批量在乘用車和新能源汽車領域推廣。隨著理論研究的深入和設計方法的完善，大幅縮短了刀具設計和加工周期，該特殊齒制齒輪將會向其他領域全面推廣。

參考文獻：

[1] 王剛強. 修形斜齒輪嚙合剛度解析模型與系統振動特性研究[D].重慶：重慶大學，2018.

[2] NI G，ZHU C，SONG C，et al. Tooth contact analysis of crossed beveloid gear transmission with parabolic modification[J]. Mechanism & Machine Theory， 2017，113：40-52.

[3] HAN Q，ZHAO J，CHU F. Dynamic analysis of a geared rotor system considering a slant crack on the shaft[J]. Journal of Sound & Vibration， 2012，331（26）：5803-5823.

[4] Fuentes-Aznar A，Gonzalez-Perez I. Mathematical definition and computerized modeling of spherical involute and octoidal bevel gears generated by crown gear [J]. Mechanism & Machine Theory，2016，106：94-114.

[5] LIU H，ZHANG C， XIANG C L，et al. Tooth profile modification based on lateral- torsional-rocking coupled nonlinear dynamic model of gear system[J]. Mechanism & Machine Theory，2016，105：606-619.

[6] LIN T，HE Z. Analytical method for coupled transmission error of helical gear system with machining errors， assembly errors and tooth modifications[J]. Mechanical Systems & Signal Processing，，2017，91：167-182.

[7] 文貴華，等.一種多壓力角雙接觸齒輪設計與制造工藝研究[J].機械設計，2021，38（8）：104-109.

[8] 文貴華，等.一種雙接觸滾齒刀[P]. 湖南：CN202639547U，2013-01-02.

[9] 潘曉東，文貴華. 齒輪及齒輪組[P]. 湖南：CN103883707B，2016-05-11.

[10] 文貴華，等. 一種雙接觸齒輪旋動干涉量的計算方法[P]. 湖南：CN102691773B，2014-09-03.

[11] 明興祖，王紅陽，金磊，等.面齒輪高速銑削表面粗糙度建模與實驗分析[J].組合機床與自動化加工技術，2020，551（1）：6-9，13.