一種非線性因子的粘性二進制粒子群算法

摘? 要：為了解決粘性二進制粒子群算法在優化過程中易陷入局部最優、全局搜索能力弱、后期收斂性能差的弊端，提出了一種非線性因子的粘性二進制粒子群算法（NFSBPSO）。NFSBPSO算法采用非線性遞減策略優化粘性權重，平衡全局與局部探索能力；同時，利用混沌策略對種群進行初始化，在每個迭代過程中對最差和最優粒子進行優化，以提高種群質量，擴大種群的全局探索能力。將新算法與3個對比算法在基準函數上進行測試，實驗表明新的算法能較好地跳出局部最優，提高了算法的穩定性和收斂能力。

關鍵詞：非線性因子；混沌策略；粒子優化；粘性二進制粒子群算法

中圖分類號：TP301? 文獻標識碼：A? 文章編號：2096-4706（2023）03-0061-05

A Nonlinear Factor Sticky Binary Particle Swarm Optimization

CHENG Qianqian

（Taiyuan Normal University， Jinzhong? 030619， China）

Abstract： In order to solve the disadvantages of sticky binary particle swarm optimization， which is easy to fall into local optimum， weak global search ability and poor late convergence performance in the process of optimization， a nonlinear factor sticky binary particle swarm optimization （NFSBPSO） is proposed. NFSBPSO algorithm uses nonlinear decreasing strategy to optimize the sticky weight and balance the global and local exploration ability. At the same time， the chaos strategy is used to initialize the population， and the worst and best particles are optimized in each iteration process to improve the quality of the population and expand the global exploration ability of the population. The new algorithm is tested on the benchmark function with three comparison algorithms. The experimental results show that the new algorithm can jump out of the local optimum better and improve the stability and convergence ability of the algorithm.

Keywords： nonlinear factor; chaos strategy; particle optimization; sticky binary particle swarm optimization

0? 引? 言

Kennedy等人于1995年提出的粒子群算法（Particle Swarm Optimization， PSO）[1]作為群智能優化算法，因其具有參數少、運算簡單和收斂速度快等特點受到廣大學者的關注，此算法多用來處理連續函數的優化。針對離散域上存在的問題，Kennedy等人于1997年進一步提出了二進制粒子群算法（Binary Particle Swarm Optimization， BPSO）[2]。BPSO算法與PSO算法相比，盡管全局搜索能力較強，但是仍不能很好地收斂到全局最優位置，并且算法的隨機性隨著迭代次數的漸增而增大，局部搜索能力越來越弱[3，4]。2019年Nguyen等人所發表的粘性二進制粒子群算法（Stickiness Binary Particle Swarm Optimization， SBPSO）[5]，采用了粘性和翻轉的思想，使算法更適用于離散問題，尋優的效果更佳。與粒子群算法相似，這些離散粒子群優化算法也存在早熟收斂問題[6-8]，相關學者針對這一問題提出了改進策略。李真等人[9]提出將灰狼算法與粒子群算法相結合，增加了粒子的收斂速度；李浩君等人[10]提出慣性權重和種群多樣性協同調整的策略，增強了算法的動態搜索的能力和種群多樣性；孫一凡等人[11]提出了一種粒度散度指標，并將模擬退火機制與粘性二進制粒子群算法相結合，平衡了算法的探索和開發能力；王皓等人[12]提出了對粒子進行鄰域搜索和擾動，加快了收斂速度。邱飛岳等人[13]利用混沌策略和成長因子來均衡全局與局部搜索的能力。王越等人[14]提出對慣性權重采用一種非線性遞增的方法，將變異算子加入速度公式中，增強了粒子的種群多樣性和尋優范圍。

雖然上述研究通過不同的策略對粒子群算法進行了優化，但在處理離散問題時，算法的性能還需要進一步的提升。本文從算法易陷入局部最優，探索和開發能力不平衡的問題出發，利用Logistic混沌策略初始化種群，采用非線性的策略改變粘性權重，并且對進化過程中對最差和最優粒子進行優化，提出了一種非線性因子的粘性二進制粒子群算法（Nonlinear Factor Stickiness Binary Particle Swarm Optimization， NFSBPSO）。

1? 粘性二進制粒子群算法

1.1? 二進制粒子群算法

傳統的二進制粒子群算法（BPSO）與粒子群算法（PSO）所用的速度更新公式一樣，而BPSO算法將映射函數應用到位置公式上，也就是說將粒子的速度映射到[0，1]區間，如果映射值小于隨機數，則位置取0，反之取1。PSO算法應用在連續域的問題上，而BPSO算法應用于處理離散域的問題。式（1）為速度更新公式，式（2）為映射函數，式（3）為位置更新公式：

（1）

（2）

（3）

其中，j為維度，vij （t+1）為粒子i在t+1次迭代的速度，w為慣性權重，c1和c2分別為自我和社會學習因子，r1和r2為[0，1]中的隨機變量，xij （t）為第i個粒子的當前位置；pbestij為個體歷史最優解，gbestij為全局最優解；T（vij （t））為映射函數，表示速度映射的概率值。

為了使PSO算法可以解決離散問題，因此引入了映射函數，但在離散問題中直接使用PSO的速度和位置公式并不能直觀的描述離散空間的速度和位置，因此有學者提出了粘性二進制粒子群算法。

1.2? 粘性二進制粒子群算法

粘性二進制粒子群算法（SBPSO）可以更加精準地描述粒子的運動狀態，即粒子的翻轉代替為粒子運動，粒子的翻轉速率則為粒子的運動速率。粘性是指在離散域中，粒子運動維持當前比特位不變的概率值。該算法在解決離散問題中效果比BPSO算法有一定的提升。速度和位置更新公式如式（4）（5）所示。

（4）

（5）

其中，xij（t）的值為0或1，is為粘性權重，stkij（t）為第i個粒子的粘性，也就是說當粒子剛發生翻轉后，stkij（t）值為1，并使該粒子保持一段時間的平衡，但粘性值會隨著迭代次數的增加而不斷衰減，直至再次翻轉或者粘性為0。SBPSO算法采用式（6）動態參數控制策略來平衡算法的探索和開發能力，相關參數如式（7）～（9）所示：

（6）

（7）

（8）

（9）

（10）

其中，is+ip+ig=1，，is_u和is_l分別為粘性權重is的上限和下限，t為當前迭代次數，T為最大迭代次數；ustk為粒子的粘性值從1衰減到0所需的迭代次數，ustk_u和ustk_l分別為ustk的上限和下限。

通過實驗發現該算法在一定條件下容易陷入局部最優。當粒子處于全局最優的位置時，翻轉概率僅由動量和粘性衰減決定，通過大量的迭代使得粘性衰減來獲得翻轉概率，這不僅耽誤了算法尋優的進程，而且不利于實現算法探索與開發之間的平衡。該算法在大型和復雜的搜索空間上表現良好，但在小型的搜索空間上尋優效果并沒有顯著提升，因此，需要對參數進行非線性的更新機制。

2? 非線性因子粘性二進制粒子群算法

2.1? 非線性因子is

粘性權重is的大小影響著算法的探索和開發的能力。當is的值較大時，提高了粒子的翻轉概率，有利于探索；當is的值較小時，降低了粒子的翻轉概率，有利于開發，避免陷入局部最優。對于粘性權重is來說，線性遞減不能有效的解決所有的尋優問題，當問題較為復雜時，局部搜索能力逐漸降低，找不到所要求的最優解。

SBPSO算法采用的典型的線性遞減的策略來改變粘性權重的值。但因為其斜率保持不變，所以翻轉概率的改變速率持續性降低，在迭代初期還沒有很好地找到全局最優解便會進入局部搜索，從而使算法陷入局部最優解。因此，采用指數函數? 對粘性權重函數進行改進。

但是在? 公式中，曲線在最高點維持的時間較短且粘性權重的值在迭代結束后不能收斂到最小值，而當t/T為六次冪且系數為-20時，最高點和最低點維持的時間均衡，有利于平衡前后期探索和開發的能力。

因此，本文提出一個非線性的is因子（Nonlinear Factor， NF），如式（11）所示，以平衡算法的探索和開發能力。非線性is曲線圖如圖1所示。

（11）

由圖1可以看出，當最大迭代次數為200次時，is在前50次迭代過程中能保持在最大值附近，可以更好地進行全局搜索，在后50次迭代過程中能保持在最小值附近，以便于迭代前期全局搜索能力與迭代后期局部搜索能力的良好平衡。

2.2? 混沌初始化策略

粘性二進制粒子群算法的初始種群是通過隨機策略生成的，其種群分布較差，質量不高。為了提高種群的質量，NFSBPSO算法采用Logistic映射進行混沌初始化，如式（12）所示：

（12）

其中，μ表示混沌程度，μ的值越大，混沌程度越高；實驗得出，當μ=4時，系統的混沌狀態最佳。在映射過程中，若xt≥0.5，xt=1；若xt＜0.5，xt=0。

2.3? 粒子優化策略

SBPSO算法在迭代過程中所有粒子會向最優粒子位置運動，造成種群多樣性降低，影響了粒子從局部最優跳出。本文通過借鑒最優粒子擾動策略和最差粒子更新策略來改進NFSBPSO算法，提高算法后期的搜索能力。

2.3.1? 最差粒子更新策略

在粒子群算法中，一直秉承著“優勝劣汰”的生存法則，為了提高最差粒子的質量，在迭代過程中其進行更新操作。最差粒子更新策略就是改進種群中適應度最糟糕的粒子，目的是增加種群的多樣性，進而提高搜索能力。最差適應度粒子改進公式如式（13）（14）（15）所示：

（13）

（14）

（15）

其中，x_worst表示適應度最糟糕的粒子；式（14）中Eworst表示更新后的粒子，也就是在每次迭代完成后，隨機性地選取三個不同的粒子進行更新。式（15）表示，如果更新后粒子的適應度值小于最差粒子，則將最差粒子更新為Eworst；反之保留最差粒子。

2.3.2? 最優粒子擾動策略

在SBPSO算法中，種群的全局最優解會影響所有粒子朝著最優解的方向移動，從而導致后期發生聚集現象，所以本文根據種群的聚集程度，對全局最優解的位置進行擾動，從而擴大種群的全局搜索能力。

判斷種群聚集程度的公式如式（16）（17）所示：

（16）

（17）

其中，avg_x表示N個粒子的中心位置，avg_r表示種群中N個粒子到avg_x的平均距離。若avg_r值較大，表示粒子分布比較散，種群多樣性較強，則對全局最優解產生的干擾較小。若avg_r值較小的話，表示粒子分布比較緊密，導致種群已經陷入局部最優或者多樣性降低，則對全局最優解產生的干擾較大。

本文采用的擾動策略如式（18）（19）所示，對全局最優解產生的擾動大小由公式中的指數函數所決定，而上文說明了擾動大小與avg_r呈負相關，因此指數函數與avg_r呈負相關：

（18）

（19）

其中Nbest（t）代表被干擾后的粒子，如果Nbest（t）的適應度值低于被干擾之前的適應度值，則被干擾后的粒子為全局最優粒子；否則不進行更新。

2.4? NFSBPSO算法步驟

本文在粘性二進制粒子群算法的基礎上，采取混沌策略、非線性粘性權重以及粒子優化策略，提出了NFSBPSO算法，算法步驟如下：

Step1：采用Logistic混沌策略初始化種群；

Step2：參數初始化；

Step3：計算適應度值，并對種群個體進行歷史最優解及全局最優解的更新；

Step4：更新非線性因子is；

Step5：對適應度值最糟糕的粒子進行改進；

Step6：針對粒子的全局最優位置進行擾動，根據擾動后粒子的適應度判斷是否需要更換全局最優解；

Step7：更新粒子的速度和位置；

Step8：對算法的終止條件進行判斷，如果滿足條件就輸出最優解；如果不滿足，則返回步驟3。

3? 仿真實驗

3.1? 實驗環境

實驗采用MATLAB語言編程，Window 10操作系統，Intel（R） Core（TM） i5-6200U CPU 處理器，主頻為2.40 GHz。

3.2? 實驗設置

本文選取了六種基準函數來對算法進行了性能測試與評價，如表1所示。F1、F2、F3是單峰函數且只具有一個最優解，可用于判斷算法的收斂性能；F4、F5、F6是多峰函數且具有多個局部最優解，可以用來判斷算法跳出局部最優解的能力。對比算法為BPSO算法[2]，SBPSO算法[5]，動態自均衡二進制粒子群算法（Dynamic self-equilibrium binary particle swarm optimization， DSEBPSO）[15]。種群規模N=30，最大迭代次數T=200。根據先驗經驗，粘性值上限 ，下限 ；自適應因子上限 ，下限 。根據文獻[5]可知α=2時，尋優效果更佳。

實驗采用以下兩種標準來評價算法的性能：

（1）均值：4個算法運行30次后，獲得最優值的均值。

（2）方差：4個算法運行30次后，獲得最優值的方差。

3.3? 實驗結果分析

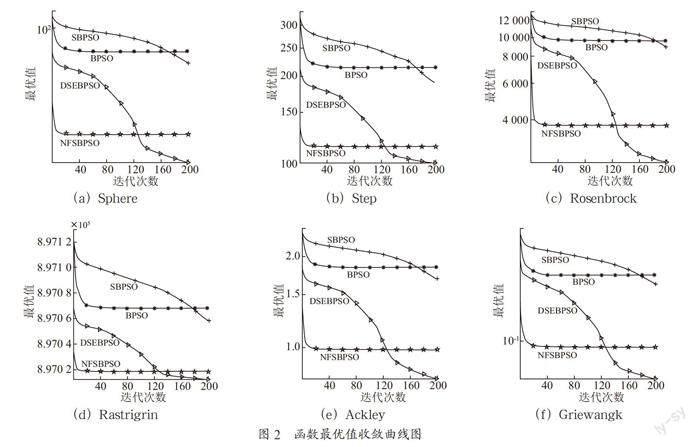
NFSBPSO算法和三個對比算法在六個基準函數上的收斂曲線如圖2所示。

由圖2可知，NFSBPSO算法在收斂速度、跳出局部最優解等方面都要比其他算法好。由于迭代時粘性權重的非線性調整，使得單峰函數在尋優過程中適應值變化迅速，尋優成功率與收斂精度也顯著增加。對于局部最優解較多的多峰函數問題，該算法使用粒子優化策略對適應度值較差的粒子加以改進，以提高其種群的多樣性，同時對全局最優粒子加以干擾，促進其跳出局部最優從而使得算法能夠做出較好的局部探索。

NFSBPSO算法和三個對比算法在六個基準函數上的實驗結果如表2所示。

單峰函數僅有一個局部最優解來檢測其收斂精度。從表2中可以看出，在單峰函數F1、F2、F3中，NFSBPSO算法的均值比其他算法好，表明該算法比BPSO、SBPSO以及DSEBPSO算法具有更高的收斂精度。多峰函數具有多個局部最優解來評價算法是否能夠跳出局部最優。從表2中可以看出，在多峰函數F4、F5、F6中，NFSBPSO算法的均值明顯好于其他算法，表明其具有更強的跳出局部最優解能力。整體來看，NFSBPSO算法的方差在單峰函數和多峰函數中，均優于其余算法，說明算法的穩定性也有了進一步的提升。

4? 結? 論

本文提出的NFSBPSO算法在參數上采用了非線性策略，使算法在收斂性能上得到了提升。為了均衡算法的探索和開發能力，在迭代過程中使用最差粒子改進策略和最優粒子擾動策略，提高了算法的尋優能力。但在運行過程中發現不斷地優化和改進使得算法的時間復雜度較高，需要在以后的工作中研究改進。

參考文獻：

[1] KENNEDY J，EBERHART R. Particle swarm optimization [C]//IEEE International Conference on Neural Networks，Perth：IEEE，1995：1942-1948．

[2] KENNEDY J，EBERHART R C. A discrete binary version of the particle swarm algorithm [C]//International conference on Systems.Orlando：IEEE，1997：4104-4108.

[3] 張鵬威.采用正弦映射與擴張算子的二進制粒子群優化算法 [J].小型微型計算機系統，2019，40（6）：1160-1164.

[4] 趙遠東，方正華.帶有權重函數學習因子的粒子群算法 [J].計算機應用，2013，33（8）：2265-2268.

[5] NGUYEN B H，XUE B，ANDREAE P，et al. A new binary particle swarm optimization approach：momentum and dynamic balance between exploration and exploitation [J].IEEE Transations on Cyberntics，2021，51（2）：589-603.

[6] 姜磊，劉建華，張冬陽，等.一種自適應變異二進制粒子群算法 [J].福建工程學院學報，2020，18（3）：273-279.

[7] PAN A Q ，WANG L，GUO W A. A diversity enhanced multiobjective particle swarm optimization [J].Information Sciences：An International Journal，2018，436-437：441+465.

[8] 徐浩天，季偉東，孫小晴，等.基于正態分布衰減慣性權重的粒子群優化算法 [J].深圳大學學報：理工版，2020，37（2）：208-213.

[9] 李真，王帆，王冉珺.一種結合灰狼算法的粒子群優化算法 [J].計算機測量與控制，2021，29（10）：217-222.

[10] 李浩君，張廣，王萬良.一種慣性權重與種群多樣性協同調整的二進制粒子群優化算法 [J].小型微型計算機系統，2018，39（3）：529-533.

[11] 孫一凡，張紀會.基于模擬退火機制的自適應粘性粒子群算法 [J].控制與決策，1-10[2022-09-03].https：//kns.cnki.net/kcms/detail/detail.aspx？dbcode=CAPJ&dbname=CAPJLAST&filename=KZYC20220512001&uniplatform=NZKPT&v=SFfl7Znyzm7G6kYM3mYnqTigMmGf3EFhaf0-oqT7JD8EXhm3pVm_PJiZON1c2qsz.

[12] 王皓，歐陽海濱，高立群.一種改進的全局粒子群優化算法 [J].控制與決策，2016，31（7）：1161-1168.

[13] 邱飛岳，王京京.自適應學習因子的混沌二進制粒子群優化算法 [J].浙江工業大學學報，2020，48（4）：411-417.

[14] 王越，邱飛岳，郭海東.一種帶變異算子的自適應慣性權重二進制粒子群優化算法 [J].小型微型計算機系統，2019，40（4）：733-737.

[15] 李浩君，吳嘉銘，戴海容.基于多維關聯本體的學習資源推薦方法 [J].浙江工業大學學報，2021，49（4）：374-383.

作者簡介：程倩倩（1997—），女，漢族，山西運城人，碩士研究生在讀，研究方向：教育軟件開發技術。

收稿日期：2022-09-21