基于Elman神經網絡的風速時間序列預測實例
李超 姜明洋

摘? 要:風速時間序列具有非線性和非平穩性的特點,傳統的預測方法難以建立風速間的函數關系,因此風速時間序列的預測結果精度不高。人工神經網絡所具有的強非線性擬合能力有效地解決了風速時間序列難以預測的痛點,文章選擇Elman神經網絡預測全國3個地區不同尺度的風速時間序列,初步探討了神經網絡風速預測的可行性。結果表明,Elman神經網絡經過訓練,具有時序非線性擬合的能力,但預測結果精度尚未提高。
關鍵詞:時間序列;風速預測;Elman神經網絡;預測精度
中圖分類號:TP18;TK81? 文獻標識碼:A? 文章編號:2096-4706(2023)03-0066-05
An Example of Wind Speed Time Series Prediction Based on Elman Neural Network
LI Chao, JIANG Mingyang
(Xinjiang Goldwind Sci & Tech Co., Ltd., Hohhot? 010010, China)
Abstract: The wind speed time series has the characteristics of nonlinear and non-stationary, and the traditional prediction method is difficult to establish the functional relationship between wind speeds, so the prediction accuracy of the wind speed time series is not high. The strong nonlinear fitting ability of the artificial neural network effectively solves the pain point of the difficult prediction of the wind speed time series. This paper selects the Elman neural network to predict the wind speed time series of different scales in three regions of the country, and preliminarily discusses the feasibility of the neural network wind speed prediction. The results show that Elman neural network has the ability of time series nonlinear fitting ability after training, but the accuracy of prediction results has not been improved.
Keywords: time series; wind speed prediction; Elman neural network; prediction accuracy
0? 引? 言
風力發電項目的總體容量在我國電力系統所占比例不斷提升[1]。由于風速具有隨機性、不穩定性以及季節性因素的影響大等特點,因此風力發電的實際功率也具有間歇性和波動性,由此給風力發電機組的輸出功率帶來較強的不確定性[2,3]。由于風電輸出功率的強波動特性,在風電聯網過程中節點電壓急劇波動,發電機組投入頻繁,進而嚴重影響電力系統的穩定運行[4]。準確、快速地預測風速模型以減少或避免風電場對電網的不良影響,提高風速和風電預測系統的預測精度,是風力發電系統安全穩定運行的必要前提和保證[5,6]。本文簡要分析了幾種預測模型的特點,根據風速時序特性,選擇神經網絡模型對全國三個地區不同的時間尺度進行了初步探索。
1? 預測模型介紹
1.1? 持久化方法
持久化方法公式如式(1)所示:
(1)
t為當前時刻,Δt為預測時間點距當前時刻t的步長,v為風速,其中基于一個共識:當前風速和近期未來風速之間存在高度相關性。即在這種方法中,當前t時風速可以認為是未來t+Δt時刻的風速。在處理非常短期的預測時,持久化方法可以顯示出良好的準確性。
1.2? 數值天氣預報方法
數值天氣預報方法數值天氣預報(NWP)建立模型需要大量信息,除數值天氣數據外,還涉及風電場的選址地形、周圍障礙物或數字地面模擬等。這種方式在氣象學中也得到了普遍應用,不需要大量的歷史時間序列數據就可以得到比較準確的結論,但由于NWP采用了高維復雜的數理方程,通常必須在巨型計算機上進行,基本無法做到時間序列的超短時間和短期預測。
1.3? 統計方法
統計方法需要使用歷史時間序列風數據,在觀察的數據量少的情況下會影響預測精度。不需要對風電場進行任何物理信息采集來建立預測模型,所需的計算資源和時間更少,主要關注風的持續特性來實現預測,但由于風所表現出的非平穩性導致統計方法的準確性不高,即統計模型不能準確地描述非線性數據統計模型。
1.4? 神經網絡方法
神經網絡方法人工神經網絡具有并行式數據處理、分布式存儲和容錯性強等特點,同時具備進行聯想存儲、非線性映射、分析與鑒別、優化設計、知識管理序列預測等的基本能力。神經網絡不需要對風電場進行物理數據采集,只需通過訓練找出準確的輸入數據(風速及數值氣象信息)與預測風速的相互作用,建立預測模型[7]。
2? 人工神經網絡
2.1? BP神經網絡
BP(Back Propagation, BP)神經網絡算法是一種非線性的數據挖掘方法。BP神經網絡由信號的正向傳播和誤差的反向傳播組成。首先是正向傳播,如果輸出層實際輸出與期望的輸出存在差,則進入誤差的反向傳播階段,不斷調整各層權值,在網絡的正反訓練學習過程中,使實際輸出接近期望輸出。
由于BP神經網絡較強的非線性擬合能力,特別是天氣預測中風速、溫度等因素的處理,以及學習規則簡單,便于計算機實現,因此目前大多利用BP學習算法進行神經網絡訓練。BP神經網絡的一般網絡結構如圖1所示[8,9]。
BP神經網絡計算主要分為兩個階段:
(1)正向過程。輸入信息從輸入層經隱藏層逐層計算各單元的輸出值:
a1=ω11x1+ω12x2+b1? ? ? ? ? ? ? ? ? ? ? ? ? ? (2)
a2=ω11x1+ω22x2+b2? ? ? ? ? ? ? ? ? ? ? ? ? ? (3)
z1=φ(a1)? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?(4)
z2=φ(a2)? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?(5)
y=ω1z1+ω2z2+b? ? ? ? ? ? ? ? ? ? ? ? ? ? ? (6)
其中,ω11…ω22為權值系數,b1,b2為偏置系數,φ(x)為激活函數。值得注意的是,激活函數通常采用非線性激活函數,而不是線性激活函數,在誤差反向傳播過程中,需對損失函數求偏導,調整各個權值,因此要求激活函數可導、連續。
(2)反向過程。反向處理誤差使得輸出層在每個層的輸入層方向上傳播以計算每個單元的誤差,并使用該誤差來校正輸入層的權重和閾值,使得校正后的網絡的最終輸出接近期望值。由于初始權重都是隨機分配的,所以如果首先計算預測結果,必然會產生預測誤差,定義預測值和實際值的函數是損失函數:
(7)
其中,Y為實際值,y為預測值,現在我們的任務就是希望通過數據集,不斷訓練學習到一個函數使得這個損失函數最小。也就是要求minE時的ω,b參數。
神經網絡根據輸入x1,x2,得到輸出y,可以列出下式:
(8)
(9)
欲使預測誤差最小即要求得E(x)最小,使用f(x)對各個參數求偏導為0,再進行迭代,例如:
(10)
2.2? Elman神經網絡
Elman神經網絡算法是目前應用較多的動態型神經網絡,在BP神經網絡隱層和輸出層之間增加了接收層結構的改進,用于隱層輸出信息的存儲作為隱式層的輸入信號再次輸入[10]。
如圖2所示,Elman神經網絡是由輸入層、隱式層、接受層、輸出層4層構成的動態反饋型神經網絡。這樣的網絡結構能夠提高對過去的數據的靈敏度[11,12]。與BP神經網絡相比,Elman神經網絡是經典的動態神經網絡,因此用于進行風速時間序列和電力負荷預測,能夠更準確地反映風速時間序列和電力負荷中的動態特性[13]。
3? 案例計算與結果分析
為了驗證Elman神經網絡的時間序列預測性能,本文選取豐鎮市、錫林郭勒盟與天津市三個地區,兩種時間尺度的風速數據進行預測實驗,并采用BP神經網絡預測結果作為對照組。
3.1? 數據歸一化
由于不同量綱和單位的輸入會影響到數據分析的結果,為了避免因維度的不同而導致數據的某些特征主導或消失,采用MATLAB的mapminmax歸一化方法將風速數據歸一化為[-1,1]區間,式(11)表示規范化的函數為:
(11)
其中,xnorm表示歸一化后的數據,x表示原始數據,xmin表示數據集中最小值,xmax表示的是數據集中最大值。
3.2? 預測模型構建
預測模型的建立需要前期數據處理完成后,建立神經網絡的模型,網絡的建立采用newff(BP神經網絡)、newelm(Elman神經網絡)命令,考慮到進行短期風速時間序列預測需要網絡快速收斂,隱層只取一層,整個Elman神經網絡由三層組成,這里輸入和輸出只有風速值,因此兩層神經元的個數都是1,隱層神經元數N由經驗公式和或組合方法確定。經驗公式為:
(12)
式中:N為隱含層神經元數,m為輸入層神經元數,為輸出層神經元數,q為任意常數。
3.3? 誤差分析模型
本文的隱層神經元傳遞函數為tansig、purelin,對Elman神經網絡進行了多次訓練,風速預測結果如圖3~圖6所示。為了更準確地評價本次預測誤差,本文引入誤差平方和SSE、平均絕對誤差MAE、均方誤差RMSE和平均百分比誤差MAPE。
(13)
(14)
(15)
(16)
3.4? 算例驗證
算例1:本算例選取內蒙古豐鎮市Merra2中尺度再分析數據,訓練集樣本點時間間隔為1 h,訓練樣本為2018年5月份小時平均風速數據,共計744個樣本點,本算例測試集為5月31日小時平均風速,共計24個預測點,預測結果如圖3、4與表1所示。
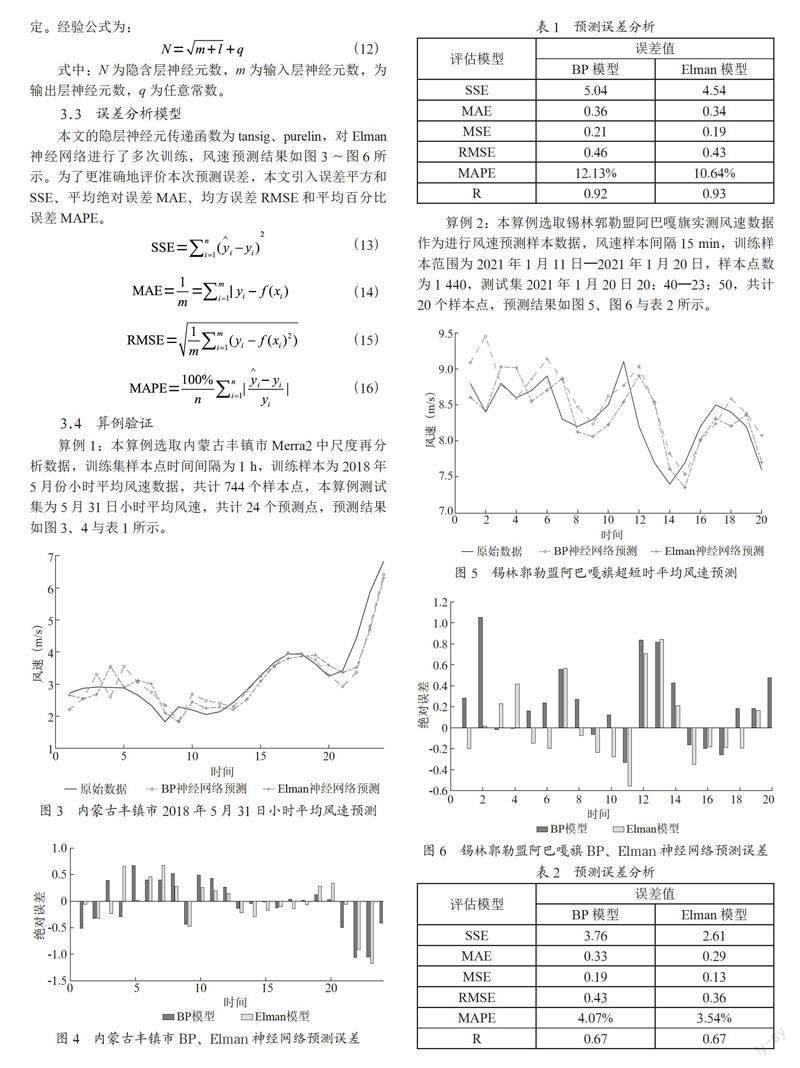
算例2:本算例選取錫林郭勒盟阿巴嘎旗實測風速數據作為進行風速預測樣本數據,風速樣本間隔15 min,訓練樣本范圍為2021年1月11日—2021年1月20日,樣本點數為1 440,測試集2021年1月20日20:40—23:50,共計20個樣本點,預測結果如圖5、圖6與表2所示。
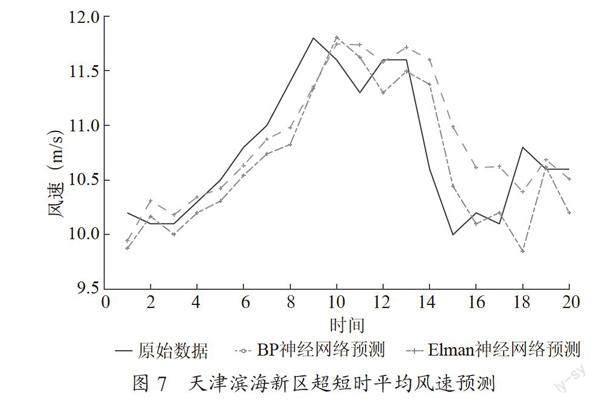
算例3:本算例選取天津市濱海新區測風塔實測風速數據作為進行預測樣本數據,風速樣本間隔15 min,訓練樣本范圍為2017年5月1日—2016年5月10日,樣本點數為1 440,測試集范圍為2016年5月10日20:40—23:50,共計20個樣本點,預測結果如圖7、圖8與表3所示。
4? 結? 論
針對風速與風功率時間序列預測方法很多,其中包括自回歸移動平均法、支持向量機、機器學習法等。其中機器學習方法中的人工神經網絡方法逐漸形成為熱門方法。已有大量研究表明,神經網絡方法更容易擬合非線性數據。
因Elman神經網絡與常規誤差反向傳播神經網絡模型相比在隱含層處多了狀態承接層,使神經網絡對歷史狀態的數據具有敏感性,相比BP神經網絡Elman神經網絡更適用于因此用它進行風速時間序列與電力負荷預測。本文選用Elman神經網絡模型對豐鎮市、錫林郭勒盟、天津市三個地區的中尺度在分析數據,實測數據進行風速數據的中期與超短期預測,并以BP神經網絡模型作為對照。預測結果說明了兩種神經網絡模型尤其是Elman神經網絡在風速時間序列預測的可行性。
Elman神經網絡與BP神經網絡預測結果精度明顯更有優,曲線擬合相關性也更高,兩種神經網絡對預測曲線極值點的捕捉存在著不足,預測精度也有待提高,Elman與BP神經網絡在風速時間序列預測方面表現欠佳主要有如下兩方面原因:
(1)輸入變量過于單一,有多重因素可以影響風速:風向、氣壓、溫度等,這些因素對風速的影響是綜合的,僅考慮單一變量輸入勢必會降低預測精度。
(2)BP、Elman等神經網絡在各個連接權值調整步驟中都使用了梯度下降法,此方式會產生訓練速度慢和易陷入局部極小點的缺陷,對神經網絡的培訓也較難實現全局最優化。
因此提高神經網絡的預測精度與普適性仍有研究前景。今后可以從增加輸入變量并研究各變量間相互影響以及輸入變量的預處理方面著手,以提高神經網絡模型在時間序列預測方面精度。
參考文獻:
[1] 張群,唐振浩,王恭,等.基于長短時記憶網絡的超短期風功率預測模型 [J].太陽能學報,2021,42(10):275-281.
[2] 曲宗希.風速組合預測策略中若干難點問題研究 [D].蘭州:蘭州大學,2019.
[3] MISHRA S P,DASH P K. Short term wind speed prediction using multiple kernel pseudo inverse neural network [J].International Journal of Automation and Computing,2018,15(1):66-83.
[4] 李歲寒.基于風電場歷史數據的短期風速及風功率預測研究 [D].蘭州:蘭州理工大學,2020.
[5] 劉海南,藺紅.考慮風電波動性的源荷優化調度策略 [J].水電能源科學,2021,39(9):210-214.
[6] 韓韞洲.風力發電功率預測的技術進展與展望 [J].電力設備管理,2021(9):130-132.
[7] 張泰豪,殷鋒,袁平.風速及風功率預測方法綜述 [J].現代計算機,2021(8):45-48.
[8] 袁曾任.人工神經元網絡及其應用 [M].北京:清華大學出版社,1999.
[9] 李海玲.基于BP神經網絡的風功率預測 [J].現代信息科技,2021,5(15):119-121+124.
[10] 張淑清,楊振寧,張立國,等.基于彈性網降維及花授粉算法優化BP神經網絡的短期電力負荷預測 [J].儀器儀表學報,2019,40(7):47-54.
[11] 林春燕,朱東華.基于Elman神經網絡的股票價格預測研究 [J].計算機應用,2006(2):476-477+484.
[12] ZHANG Y,WANG X P,TANG H M. An improved elman neural network with piecewise weighted gradient for time series prediction [J].Neurocomputing,2019,359(C):199-208.
[13] 李琛,郭文利,吳進,等.基于BP神經網絡的北京夏季日最大電力負荷預測方法 [J].氣候與環境研究,2019,24(1):135-142.
作者簡介:李超(1994—),男,漢族,內蒙古呼和浩特人,高級風資源工程師,學士學位,研究方向:新能源科學與工程。
收稿日期:2022-10-04

