基于卡爾曼濾波的UWB室內精確定位研究
張敏 楊瑞 管艷

摘要:高精度的定位系統對促進數字化時代的發展尤為重要。文章針對室內復雜環境的定位問題,建立基于線性卡爾曼濾波的定位模型,有望提高室內定位的精確度。文章首先根據UWB原理,利用三邊定位法計算靶點坐標。其次使用卡爾曼濾波算法對坐標數據進行平滑處理,以減小因干擾信號引起的數據誤差。最后模擬室內靜態實驗得到10組濾波前后的靶點坐標及其誤差值。結果表明,本研究的定位模型明顯提高了定位精度,對復雜環境下的定位具有一定的應用價值。
關鍵詞:室內定位:卡爾曼濾波:UWB;復雜環境
中圖分類號:TN92 文獻標志碼:A
0 引言
大數據時代背景下,萬事萬物都向著智能化方向發展。人們對定位技術的準確性和穩定性的要求也越來越高,因此研究高精度的定位系統顯得尤為重要。現有的國內外定位系統以衛星定位為主,這類系統雖然在導航的使用領域和室外定位的應用十分廣泛。但由于復雜區域的信號受阻,使得其在室內的定位精度并不理想,故無法滿足人們對復雜區域高精度定位的需求[1]。隨著技術的更新迭代,諸如紅外線、超聲波等定位技術相繼出現。但其在定位精度或是系統功耗方面仍有缺陷。
超寬帶( UWB)是一種短距離高速無線通信技術。其具有對信號衰落不敏感、安全性高、系統復雜度低及定位精度高等特點[2]。UWB技術可以與現有的無線通信系統做到頻率資源共享,進而提高頻譜利用率,實現高速率通信。然而UWB存在許多干擾問題,例如,與現有無線通信系統因頻譜重疊導致干擾、多徑干擾及UWB系統相互干擾,這已然成為制約UWB技術發展的重要因素。針對此類問題,本文提出一種基于卡爾曼濾波的UWB定位模型。該模型主要用于解決UWB中因各類干擾引起的定位誤差大和定位點漂移等問題,從而實現高精度定位。
1 定位原理及方法
1.1
UWB定位原理
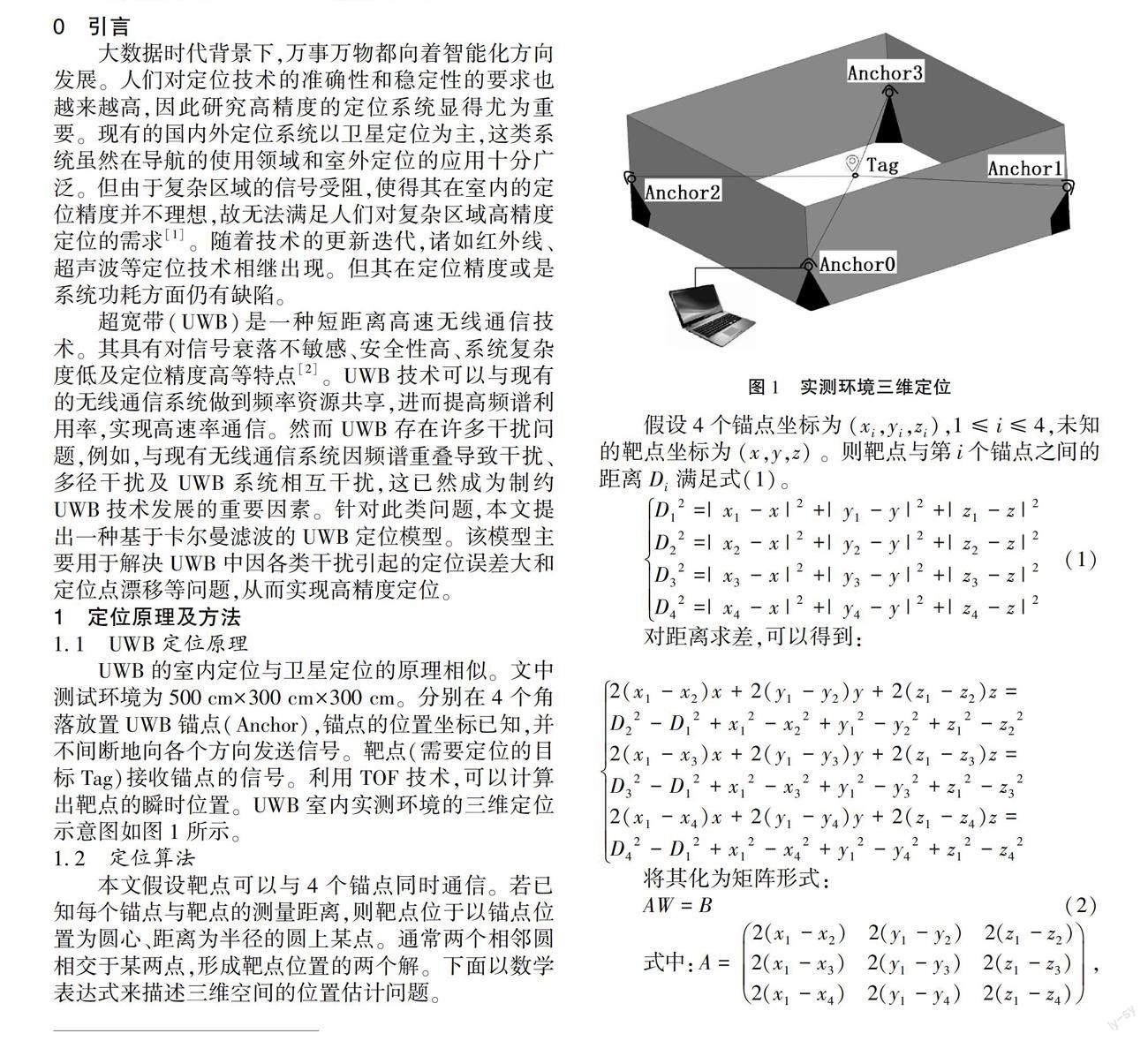
UWB的室內定位與衛星定位的原理相似。文中測試環境為500 cmX300 cmX300 cm。分別在4個角落放置UWB錨點(Anchor),錨點的位置坐標已知,并不間斷地向各個方向發送信號。靶點(需要定位的目標Tag)接收錨點的信號。利用TOF技術,可以計算出靶點的瞬時位置。UWB室內實測環境的三維定位示意圖如圖1所示。
1.2 定位算法
本文假設靶點可以與4個錨點同時通信。若已知每個錨點與靶點的測量距離,則靶點位于以錨點位置為圓心、距離為半徑的網上某點。通常兩個相鄰圓相交于某兩點,形成靶點位置的兩個解。下面以數學表達式來描述三維空間的位置估計問題。
綜上,根據最小二乘法可以計算出靶點的三維坐標。
W= (ArA) -'ArB
(3)
1.3 基于線性卡爾曼濾波的定位模型
卡爾曼濾波目前已經廣泛地應用于制導與控制、導航和通信等多個領域。其可理解為一種遞歸算法,即根據當前的測量值、前一時刻的預測值和誤差,遞歸當前時刻,再預測后一時刻的狀態估計法[3]。由于室內定位環境復雜,文中采用卡爾曼濾波法對解算后的位置坐標進行平滑處理,盡可能地消除因外界脈沖干擾帶來的測量誤差。
(1)計算出靶點的三維坐標。
已知測試環境中錨點位置(單位:cm)為Al(O.0.120)、A2 (500.0. 160)、A3(0,300. 160), A4( 500.300,120)。假設錨點和靶點之間的信號傳播在視距范圍內。靶點采集到10組相關數據,并提供了錨點與靶點的距離值( cm)。其中前5組數據無信號干擾,后5組數據有信號干擾。此處選取一組數據(330,313,290,279),根據定位算法得到相應的靶點坐標見式(4)。
2 結果與討論
本節旨在使用卡爾曼濾波對UWB定位后的坐標數據進行平滑處理,以減小數據誤差,從而提高定位精度。下面進行模擬環境下的靜態定位測試。
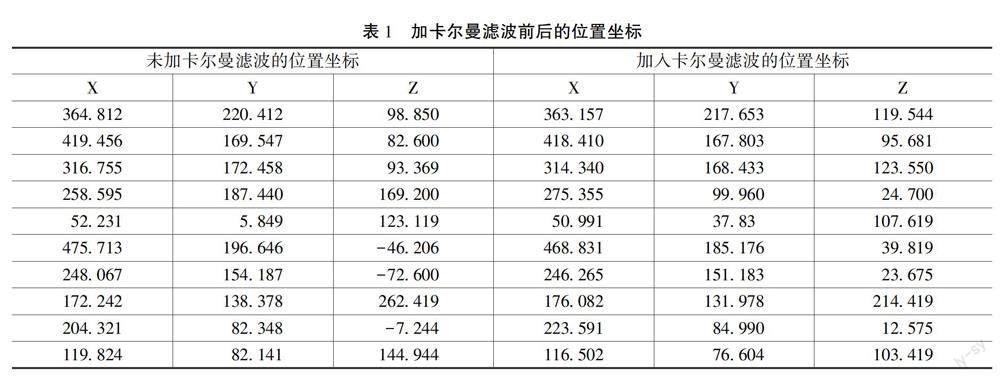
首先,基于靶點采集到的數據,通過定位算法得到靶點坐標。然后,利用Matlab中的Simulink模塊搭建Kalman位置模型。最終得到10組優化前后的靶點坐標如表1所示。
表1表明了加入卡爾曼濾波后的位置坐標更加合適,提高了定位精度。并且卡爾曼濾波算法相較于其他算法而言,執行速度更快。為了更直觀地觀察加入卡爾曼濾波的效果,如圖2所示給出了濾波前后10組數據的誤差值。
從圖2可以清晰地看出加入卡爾曼濾波進行平滑處理后的數據誤差明顯減小,且較為平穩。相比于未加入濾波前的位置數據而言,濾波后的數據更具有參考性。
3 結語
本文提出了一種基于卡爾曼濾波的UWB室內精確定位技術,旨在解決UWB定位技術的測量精度不夠高的問題。具體地依據UWB定位原理以及靶點采集到的數據得到靶點坐標,結合卡爾曼濾波法對坐標進行了平滑處理。并且通過分析模擬實驗的靜態定位誤差,證實了本文的定位模型一定程度地提高了定位精度。該方法能夠更加準確、可靠地定位。但室內環境較為復雜,該定位技術必要時需進行趨勢分析和補償,進一步提高該模型應用的魯棒性。
參考文獻
[1]劉永昌,龔元明.基于卡爾曼濾波的超寬帶定位技術應用[J].軟件工程,2021(7):24-27.
[2]陳煒翰,李世銀.基于超寬帶和微慣導組合的室內精確定位[J].電子元器件與信息技術,2020(1):24-26.
[3]楊玉林.基于卡爾曼濾波和粒子濾波的目標跟蹤性能對比[J].佳木斯大學學報(自然科學版),2021(3):72-75,78.
[4] CHEN C, WU X, BO Y, et al.SARSA in extendedKalman Filter for complex urban
environmentspositioning[J].International Journal of Systems Science,2021(18):1-16.
[5lSAINZ J J,REVESTIDO H E, LLATA J R,et al.LQG control for dynamic positioning of floating caissonsbased on the Kalman fiher[J].Sensors. 2021( 19): 1065.
(編輯傅金睿)

