基于滑模方法的不確定分數階廣義系統的魯棒無源控制?

張程程, 任啟峰??, 考永貴, 高存臣

(1. 中國海洋大學數學科學學院, 山東 青島 266100; 2. 哈爾濱工業大學(威海)理學院, 山東 威海 264209)

分數階微積分是對任意階導數和積分的探索,從數學上講,它是對經典微積分學的延伸[1]。分數階導數具有歷史記憶的特性,也越來越多地出現在控制科學和工程領域的應用之中。對分數階系統的穩定和控制問題進行深入研究是十分必要的,現已有大量相關成果[2-8]。例如,文獻[2]研究了針對分數階系統的二次型李雅普諾夫函數,文獻[3]將李雅普諾夫直接法推廣到非線性分數階系統,并給出了分數階系統的Mittag-Leffler穩定的定義及充分判據,文獻[4]研究了時滯分數階神經網絡的Mittag-Leffler同步問題,文獻[5-6]研究了分數階廣義系統的鎮定問題。

滑模控制是研究魯棒控制問題的一種有效方法[9-10]。近年來,滑模控制也被應用到分數階系統中,提出了各種分數階滑模控制策略和方法[11-15]。文獻[11-12]研究了針對分數階混沌系統的魯棒滑模控制器設計問題。文獻[13]將滑模控制用于線性多變量分數階系統的魯棒調節問題。文獻[14]設計了基于擾動觀測器的分數階系統的滑模控制器。文獻[15]研究了分數階系統的高階滑模觀測器問題。現有的分數階滑模控制經常采用整數階滑模控制的方法,即對滑模切換函數和李雅普諾夫函數求取一階導數,進而獲得等效控制并研究滑動模態的穩定性。然而,研究并發展分數階的滑模控制方法和分數階穩定性理論似乎會更有意義,例如構造分數階型的切換函數并求分數階導數。

無源性理論可以保持系統內部的穩定,這在控制理論中起著非常重要的作用。基于李雅普諾夫函數的穩定性理論也可以用無源性來解釋,可以說是對穩定性的一種更高層次的抽象。然而,以往關于無源性的討論主要集中在整數階系統的情況下[16-18]。據作者了解,分數階廣義系統的無源性分析尚未得到研究,本文首次嘗試對具有時變不確定參數的分數階廣義系統進行魯棒無源性分析。

針對一類含擾動的不確定分數階廣義系統,本文基于滑模方法討論了其具有無源性能的魯棒可容許性問題。本文工作的主要貢獻可概括為以下兩方面:

(1)對帶外部擾動的不確定分數階廣義系統設計分數階積分型切換函數,利用分數階穩定性理論對滑動模態進行穩定性分析并給出充分條件。

(2)首次給出不確定分數階廣義系統魯棒無源可容許性的充分性判據。

1 問題描述

考慮一類時變不確定分數階廣義系統

(1)

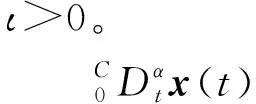
定義1[5]分數階廣義系統

(2)

被稱為是

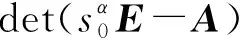
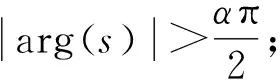
(Ⅳ)可容許的,如果系統同時是正則的、無脈沖的和漸近穩定的。

定義2分數階廣義系統(1)被稱為是魯棒無源的,當u(t)=0時,如果存在常數γ>0使得下式

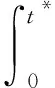
對任意t*>0和任意可容許的系統不確定性在零初始情況下都成立。

定義3分數階廣義系統被稱為是具有無源性能的魯棒可容許的,如果系統對任何可容許的不確定性同時滿足魯棒無源性和可容許性。

引理1[2]對于分數階系統

(3)

如果x(t)=0是系統的平凡解,則系統(3)被稱為是

(Ⅰ)穩定的,如果任意x(t)≠0使得xT(t)·f(x(t))≤0成立;

(Ⅱ)漸近穩定的,如果任意x(t)≠0使得xT(t)·f(x(t))<0成立。

引理2[19]Y和Z是具有合適維數的實矩陣,對任何滿足VTV≤I的矩陣V及常數ε>0,不等式

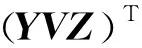
成立。

2 主要結果

本節針對分數階廣義系統設計了分數階積分型切換函數和分數階滑模控制方法,依次解決下面三個問題:

(1)如何設計分數階積分型切換函數并得到滑動模態方程?

(2)如何確保滑動模態具有魯棒無源性和可容許性,給出對應的充分條件,并確定控制反饋增益矩陣?

(3)如何設計滑模控制律使狀態軌跡可以到達預設的切換面?

2.1 分數階積分型切換函數

分數階積分型切換函數設計如下:

(4)

式中:G∈Rm×n需滿足GB1可逆;K∈Rm×n是控制反饋增益矩陣,將在后文給定。

根據分數階微積分的性質[1],Ex(t)可改寫為

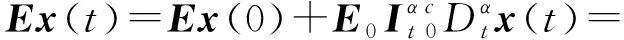
(5)

將式(5)代入式(4),積分型切換函數變形為

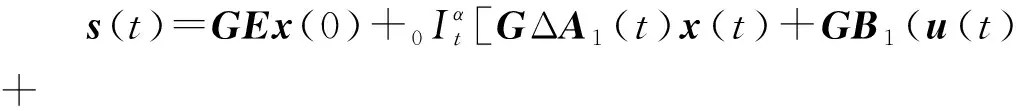
對s(t)求α階導數得

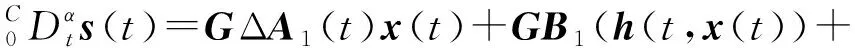
(6)

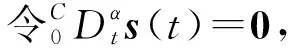
ueq(t)=-(GB1)-1G(ΔA1(t)x(t)+B2ω(t))-
h(t,x(t))+Kx(t)。

(7)

將式(7)代入式(1),滑動模態被表示為

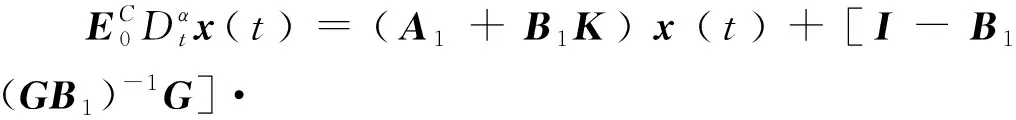
(8)

因此,滑動模態(8)和系統(1)中的輸出方程可寫作

(9)

2.2 具有無源性能的魯棒可容許性分析

本小節研究式(9)中滑動模態和輸出方程的魯棒無源性和可容許性問題,具體分為兩步:第一步,假設系統(9)中包含矩陣K在內的所有矩陣都是已知的,給出系統(9)在滿足無源性條件下的魯棒可容許充分判據。第二步,確定控制反饋增益矩陣K,使系統(9)實現具有無源性能的魯棒可容許性。

定理1給定常數γ>0,分數階系統(9)是具有無源性能的魯棒可容許的,如果存在矩陣P∈Rn×n和常數ε>0,使得

PTE=ETP≥0,

(10)

證明 首先考慮標稱情況,當系統(9)中的不確定項ΔA1(t)=0和ΔC1(t)=0時,系統(9)被寫作

(11)

構造李雅普諾夫函數

V(x(t))xT(t)PTEx(t)。

對V(x(t))求α階導數,可以得到

令

結合式(10)可知χ<0,因此

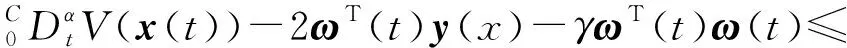
(12)

對上式不等號兩側作關于t的[0,t*](?t*>0)區間上的一階積分,由于V(x(t))>0,故

(13)

在零初始條件下成立。因此,對?t*>0,

在零初始情況下成立,故分數階系統(11)是魯棒無源的。

并且,當ω(t)=0時,根據式(12)和引理1,可知系統(11)同時是漸近穩定的,由定義1進而實現可容許性。

(14)

代替χ。根據引理2可知

(15)

注1無源性問題早已被研究過,但它們的結果是在整數階情況下建立的[16-18]。需要注意的是,為分數階廣義系統構建適當的無源性標準并不是一項簡單的任務。本文巧妙地利用區間參數和分數階微積分的性質,解決了參數間切換的復雜性。

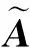
定理2給定常數γ>0,系統(9)是具有無源性能的魯棒可容許的,如果存在常數ε>0,矩陣H∈Rm×n和L∈Rn×n,使得

(16)

證明 結合Schur補定理,由式(16)可得

(17)

利用diag{L-T,I,I}對式(17)做合同變換,因合同變換不改變負定性質,再結合H=KL可得

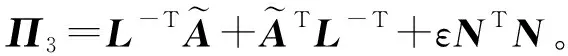
2.3 滑模控制律

本小節設計了滑模控制器,使系統(1)中的狀態軌跡在其作用下可以到達切換面。

定理3切換函數s(t)由式(4)給出,s(t)中的矩陣G滿足GB1可逆,矩陣K由定理2得到。設計滑模控制器如下:

u(t)=Kx(t)-(GB1)-1(‖GM1‖‖Nx(t)‖+
ι‖GB1‖‖x(t)‖+‖GB2‖‖ω(t)‖+ρ)·
sgn(s(t)),

(18)

式中ρ>0,系統(1)的狀態軌跡可以到達切換面s(t)=0。

證明 將u(t)代入到式(6)中得到

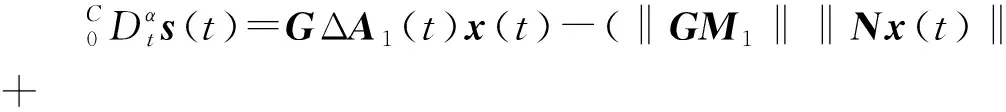
(19)

選取李雅普諾夫候選函數

對Ψ(t)求α階導數,從而得到

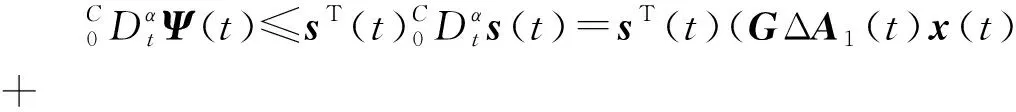
(20)

其中sT(t)sgn(s(t))≥‖s(t)‖。因此,狀態軌跡可以到達切換面。

3 數值算例

對不確定分數階廣義系統(1)賦予如下參數:

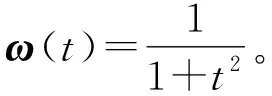
利用MATLAB軟件對定理2中的式(16)進行求解,可得ε=0.6,矩陣

H=[0.476 0 0.423 8 -0.571 2],

從而K=[-1.750 4 -2.607 1 -3.103 3]。取參數ρ=0.01,給定初始條件x0=[-10 6.8 9.5]。結合上述所有給出的條件,仿真結果如圖1～3所示,圖1代表的是狀態軌跡x(t),圖2描述的是切換函數s(t),圖3表示的是控制器u(t)。

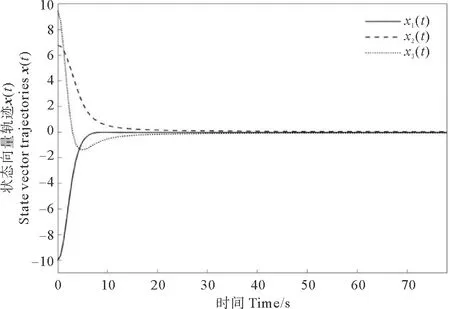
圖1 狀態向量軌跡x(t)Fig.1 State vector trajectories x(t)

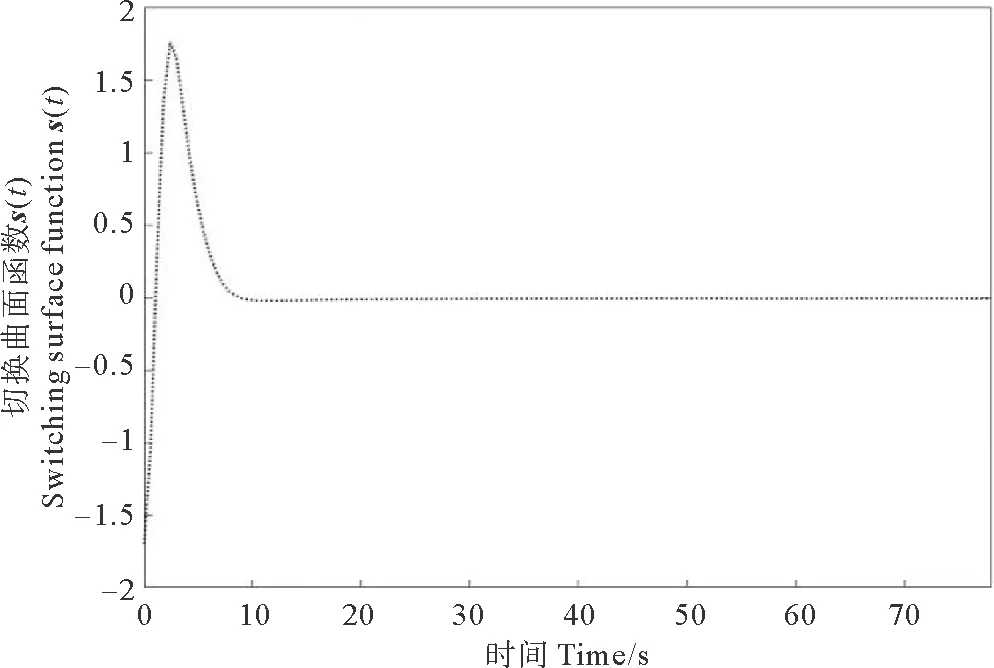
圖2 切換曲面函數s(t)Fig.2 Switching surface function s(t)

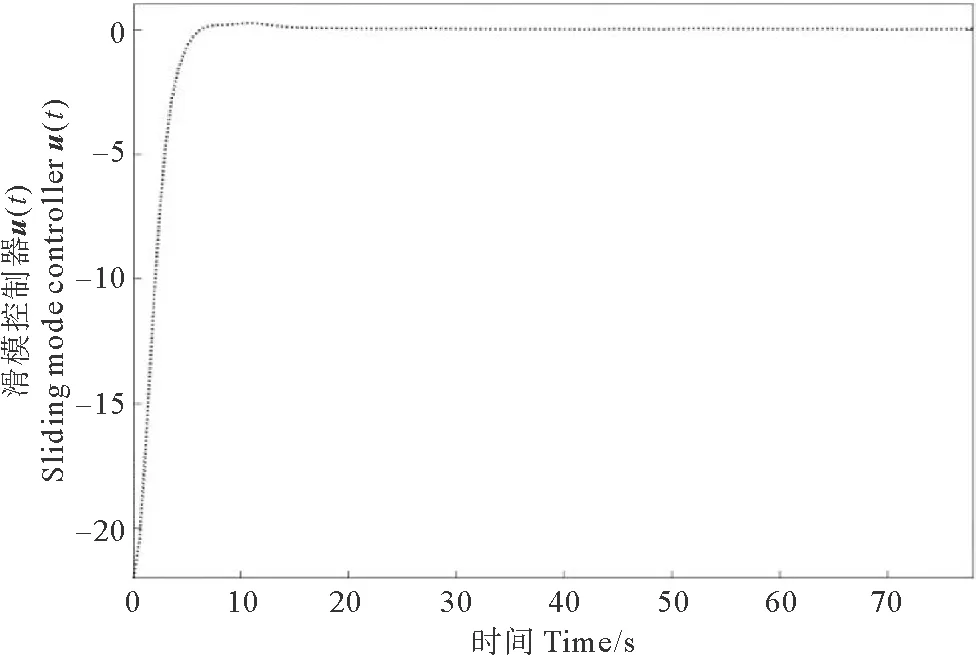
圖3 滑模控制器u(t)Fig.3 Sliding mode controller u(t)

4 結語

本文針對帶外部擾動的不確定分數階廣義系統設計了分數階積分型切換函數,計算了切換函數的分數階導數并使其為0,得到了等效控制,設計了滑模控制器使狀態軌跡到達切換面。利用區間參數和分數階微積分的性質,通過線性矩陣不等式首次給出了滑動模態具有無源性能的魯棒可容許性的充分性判據,并且解決了滑動模態的魯棒無源化問題。本文給出的魯棒無源分析方法也可嘗試推廣到分數階奇異攝動系統和分數階時滯系統。