基于證據理論的支擋型黃土高陡邊坡穩定性評價

李 哲 劉 彤 劉路路,2,3 韓 猛,4 官宸慧,5 張庭順

(1長安大學公路學院, 西安 710054)

(2東南大學交通學院, 南京 211189)

(3中國礦業大學深部巖土力學于地下工程國家重點實驗室, 徐州 221116)

(4大連理工大學土木工程學院, 大連 116024)

(5武漢大學土木工程學院, 武漢 430072)

隨著國家“一帶一路”和“交通強國”發展規劃的提出,我國高速公路、鐵路建設正向地勢復雜,地形多以山谷、高原和丘陵為主的西北黃土高原地區快速發展,而更為復雜的地質環境則為邊坡設計帶來了挑戰,并進一步對高陡邊坡穩定性的研究提出了更高的要求[1-3].現有的研究常集中于低邊坡坡面的穩定性,忽略了支擋結構的穩定性,而高陡邊坡的穩定性由邊坡坡體和支擋結構兩者共同決定[4-6],因此將二者有機結合并建立完善的評價體系是亟待解決的問題.

近年來,國內外不少學者對邊坡的安全評價問題進行了大量研究,提出了一些邊坡穩定性評價方法[7-9].人工神經網絡具有自組織、自學習的特點,能較好地處理邊坡的非線性映射,但推理過程不透明,部分影響因素采用人為賦值的方法計算.Acharyya等[10]建立了一個人工神經網格,對條狀地基的極限承載力進行了評價,并按其重要程度進行了分類;李蕾[11]利用GA-LM-BP人工神經網絡對某特定自然降水環境下的邊坡進行了穩定性分析.灰關聯法是信息較少時系統的有效方法,但在進行聚類分析時,主觀判斷對功效函數的確定影響很大.Hao等[12]提出了一個基于區域劃分的灰色體系模型,來研究人為因素對流域的作用;馮忠居等[13]基于灰色系統原理,提出用于混凝土動態彈性模量的動態響應模型.模糊綜合評價法采用隸屬函數評價邊坡穩定性,該方法具有系統性強、結果清晰的特點,但各指標權重的分配人為主觀因素多.Greco等[14]、Zeng等[15]建立了模糊評價模型,研究巖石跳動距離計算方法和典型滑坡前期預報;孫欣[16]用模糊綜合評判法和GIS技術評價邊坡穩定性,評價結果與數值模擬結果吻合.還有學者用可靠度分析邊坡的穩定性,如羅強等[17]采用可接受部分單元邊坡失穩的K/N(F)系統模型,對長區段路基邊坡系統安全性進行概率評價;朱聰聰[18]將可靠度理論引入到高邊坡工程的穩定性分析中,得到了高邊坡失穩的可靠性指數和發生失穩的概率.有時僅用一種方法并不能很好地評價邊坡穩定性,可將2種或多種方法相結合進行研究.如張學喜[19]提出了一種將BP神經網絡與各因子的非線性關系相結合的快速遺傳算法,用以評價邊坡穩定性;夏煒洋[20]基于灰色關聯度分析影響邊坡穩定性因素的關聯性,結合BP神經網絡對邊坡的發展趨勢進行了預測.

由于支擋型黃土高陡邊坡穩定性評價具有模糊性和不確定性,與上述方法相比,D-S證據理論的推理程序更為嚴密,且對信息的整合更為完備,并且評價精度較高,但目前在邊坡穩定性評估中引入證據推理方法的研究尚少.本文應用邊坡穩定性評價體系,建立評價模型,對包茂高速典型支擋型高陡邊坡進行安全評價,并得出邊坡變化過程中各參數隨時間變化的動態變化規律,從而為類似工程穩定性評價提供新思路.

1 D-S證據理論及基于證據理論的評價方法

1.1 基本函數

證據理論是由Dempster于1967年提出的一種不精確推理理論,也稱為D-S證據理論,在解決受多因素、多指標影響下的不確定性問題方面應用廣泛,尤其是其計算公式被廣泛地用于數據融合[21-24].Shafer[25]將在模式識別中判定的問題所有可能的答案都包含在一個非空有限集合Θ中.

定義1設Θ為辨識框架,R為冪集2Θ中一個集類,A為Θ的子集,若函數m:R→[0,1]滿足

(1)

函數m為辨識框架上的基本概率分配函數,對任意的命題A,m(A)稱為命題A的基本概率分配.

定義2設Θ為辨識框架,R為冪集2Θ中一個集類,A為Θ的子集,m為Θ上的mass函數,Bel:R→[0,1]滿足

(2)

Bel稱為辨識框架Θ上的置信函數,對任意的命題A,Bel(A)稱為命題A的可信度,表示給予命題A的全部的可信程度.

1.2 基于證據理論的不確定性多指標評價方法

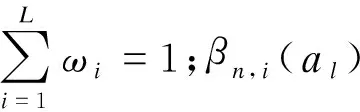
mn,i(al)=ωiβn,i(al)
i=1,2,…,L;l=1,2,…,S

(3)

(4)

式中,mn,i(al)(i=1,2,…,L)表示Ek(i)前i個指標支持假設E被評為Hn等級的置信度;mH,i(al)表示未分配給前i個指標的置信度.

(5)

(6)

2 安全評價模型

2.1 識別框架建立

根據巖土邊坡穩定性評價常采用的穩定級別,將穩定性分為4個等級(見表1)[27]:安全狀態、基本安全狀態、臨界狀態、破壞狀態.這4種評價結果完整地描述了某一邊坡安全狀態且相互排斥,即Θ={Ⅰ,Ⅱ,Ⅲ,Ⅳ}.

表1 支擋型黃土高陡邊坡穩定性等級評價標準

2.2 基本概率分配函數的確定

目前廣泛使用的是康兵義等[28]提出的基于區間的基本概率分配函數生成方法,下面簡單介紹區間的定義.

定義3設A=[a1,a2]和B=[b1,b2]為2個區間,則它們距離的二次方D2為

(7)

定義4設A=[a1,a2]和B=[b1,b2]為2個區間數,則區間A、B的相似度S(A,B)為

(8)

式中,α>0為支持系數;D(A,B)為區間數A和B之間的距離,可以調節相似性數值的離散度.

采用區間求解基本概率分配的具體步驟如下:

① 將確定的基本指標的區間劃分結果作為區間數模型.

② 將各指標的試驗數據、監測數據取值構成的區間作為識別區間.

③ 根據式(7)計算2個區間之間的距離.

④ 根據式(8)計算2個區間之間的相似度.

⑤ 對相似度進行歸一化處理,即可得到基本概率賦值.

2.3 D-S置信度公式

在得到基礎概率數值后,再計算權重的基礎概率賦值.指標基礎概率分布的計算過程如式(3)～(6)所示.根據Yang[26]的觀點,在邊坡安全評價時所選擇的基本指標中,既有定量指標如日降雨量、孔隙水壓力等,也有定性指標如邊坡形態、坡體裂隙等.定性指標是指需要將評價指標在各自辨識框架上的置信度轉到總的辨識框架上,轉移后置信度和不確定度的計算過程如下:

(9)

Hn:βn(al)=δmn,l(L)(al)

(10)

(11)

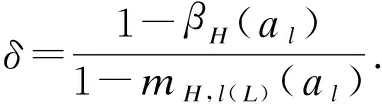
2.4 支擋型黃土邊坡指標選擇

支擋型黃土邊坡安全性評價指標分為邊坡坡體和支擋結構2個方面.邊坡坡體穩定性的影響因素眾多,內部因素主要包括土的性質、結構、地應力以及土體中水的作用等;外部條件主要包括氣象特征、地震、邊坡形態的改變等.因此,在進行邊坡坡體體系構建時,需要全面考慮影響坡體穩定的內外因素.對于自身不穩定的邊坡,采用支擋結構是目前比較常用的手段之一.本文支擋結構以抗滑樁為例,當邊坡失穩時,滑坡產生的滑坡推力作用在抗滑樁上,抗滑樁將滑坡推力傳遞到下部穩定的土層中,依靠土體自身的抗力抵抗滑坡推力.支擋型邊坡安全評價指標體系如表2所示.

表2 支擋型黃土高陡邊坡安全評價指標體系

3 工程實例分析

3.1 工程背景

包茂高速G65W陜西境黃陵至延安高速公路所處地區由于其地形屬黃土高山峻嶺,塬面坡度較陡,容易發生滑坡等災害,且多處黃土塬已經成為黃土嶺,兩側滑坡現象很嚴重,此處高陡邊坡綜合坡率在1∶1.07～1∶1.42之間,100 m以上的邊坡有6個.本文選取最大高度的萬花邊坡,采用提出的證據推理方法進行安全評價,標段為LJ-19,屬于舊滑坡,邊坡級數為15級,抗滑樁長度40 m,其余參數如表3所示.萬花邊坡及其地質剖面圖如圖1所示.

(a) 萬花邊坡

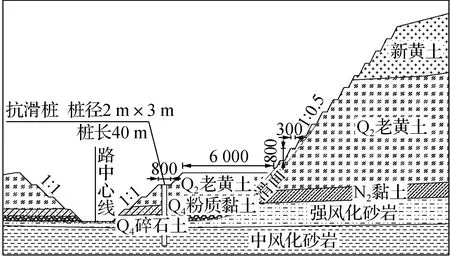
(b) 地質剖面圖(單位:cm)

表3 目標邊坡參數

本文通過室內試驗、現場試驗以及現場監測等方法獲得基本指標的取值,建立支擋型黃土高陡邊坡安全評價指標框架體系,結果如表4和表5所示.位移采用固定式測斜儀進行監測,利用自動采集系統進行數據采集,本文取最大位移作為區間劃分依據.

表4 目標邊坡土體物理力學參數表

表5 目標邊坡指標實測值

3.2 安全評價指標區間劃分

以降雨量為例,確定降雨量指標區間劃分過程.利用野外設置的降雨測量儀對降雨情況進行監測,利用在邊坡上設置的孔隙水壓力傳感器對邊坡土壤進行檢測.水平位移與累計降雨量關系如圖2所示,由圖可知,黃土斜坡土體內部位移隨降雨量的增加逐漸增大.土體位移與入滲深度的關系如圖3所示,0.4 m深度處土體的位移較大,并呈現出明顯的階段性特點,且試驗過程中該部分土體發生了明顯的滑移現象.因此,以0.4 m深度處土體位移的變化趨勢確定累計降雨量的區間限值.

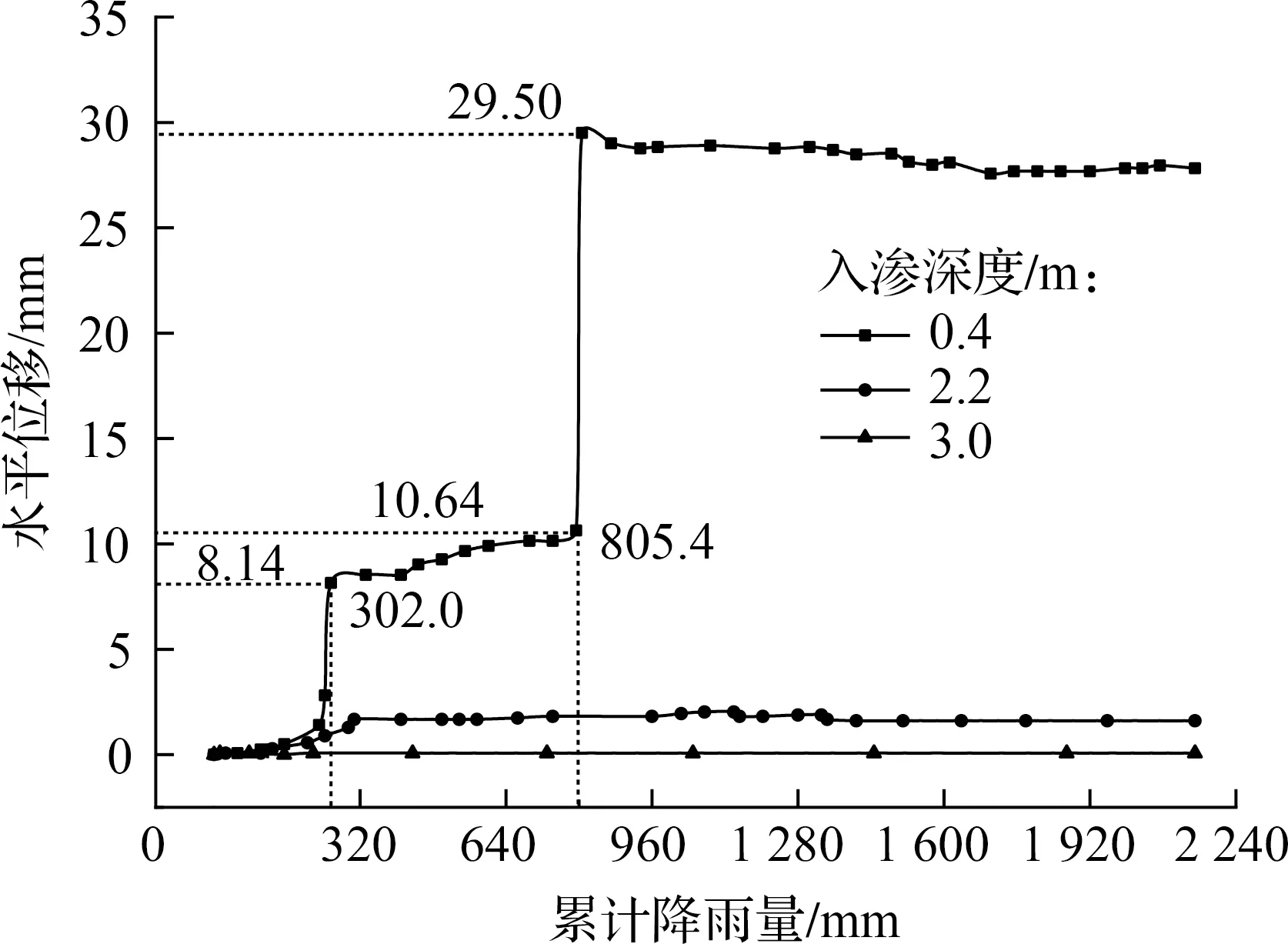
圖2 水平位移與累計降雨量關系曲線圖

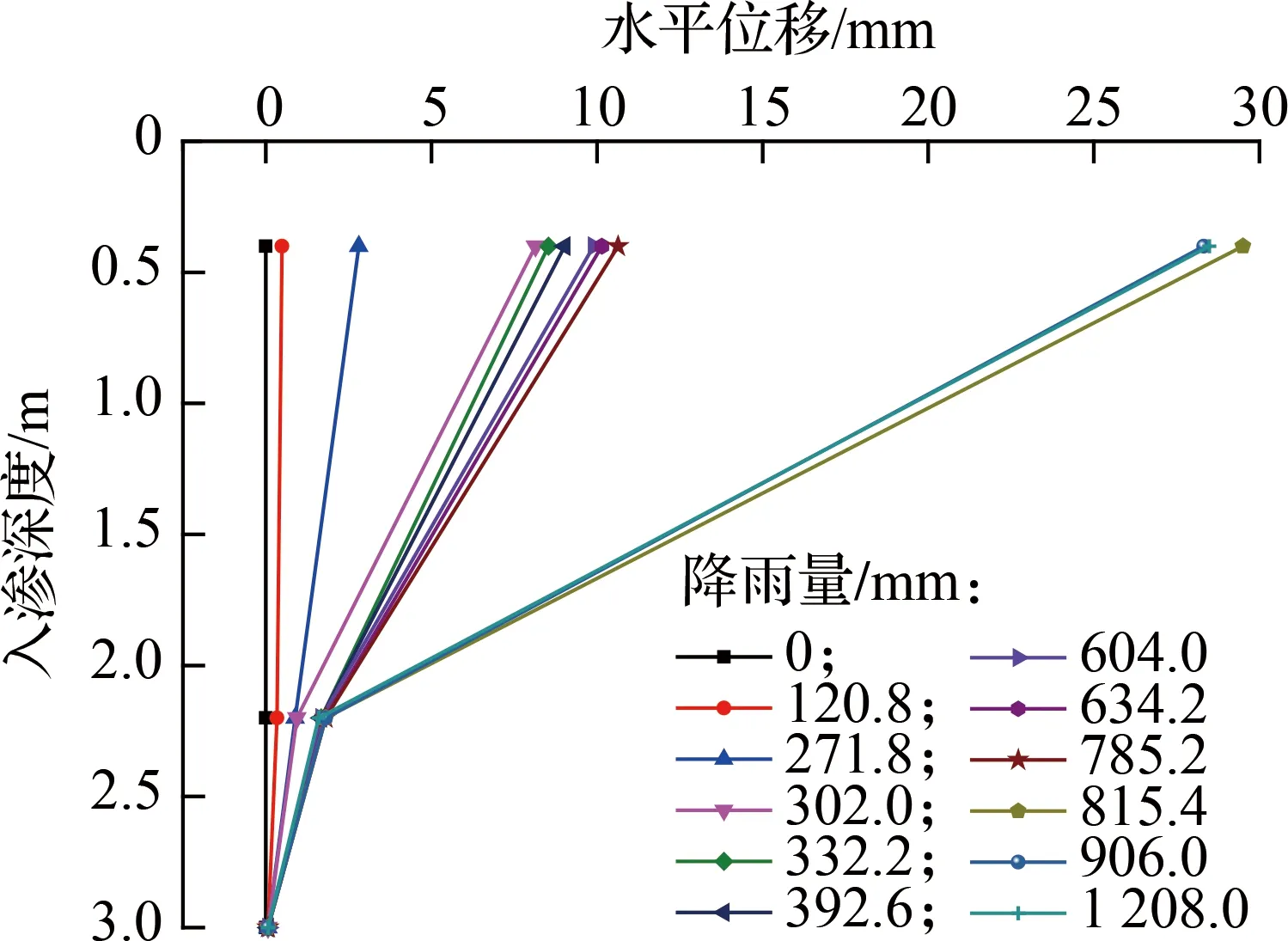
圖3 水平位移與入滲深度關系曲線

在30.2 mm/h的降雨強度作用下,0.4 m深度處土體發生滑移,土體位移隨降雨量的變化明顯分為4個階段:① 第1階段,累計降雨量從0增加至120.8 mm,土體位移基本保持不變.②第2階段,累計降雨量從120.8 mm增加至271.8 mm,土體累計水平位移從0.07 mm增加到1.4 mm,邊坡土體位移緩慢增加,但變化量不大.③ 第3階段,累計降雨量從271.8 mm增加至724.8 mm,當累計降雨量為302 mm時,土體位移由1.40 mm迅速增加至8.14 mm,且隨著降雨的持續繼續保持緩慢增長,此時該部分土體已經處于不穩定狀態.④ 第4階段,累計降雨量超過724.8 mm,當累計降雨量為815.4 mm時,邊坡土體位移由10.64 mm迅速增加至29.50 mm,且隨降雨的持續基本保持不變,此時該部分土體已經發生明顯的滑移現象.基于以上降雨作用下土體位移隨累計降雨量的增加呈現出明顯的階段性的特點,以累計降雨量為指標,將降雨對邊坡位移的影響分為4個階段,得到黃土邊坡安全評價等級的標準,如表6所示.

表6 邊坡安全評價基本指標區間劃分

基于數值模擬以及抗滑樁縮尺模型試驗的結果,對土體位移、抗滑樁內力及抗滑樁位移等基本評價指標進行區間劃分.土體物理力學特性指標基于室內反復直剪試驗和壓縮試驗的結果進行劃分,孔隙水壓力和日降雨量根據黃土斜坡人工降雨試驗進行劃分.具體劃分結果如表7所示.

表7 邊坡安全評價基本指標區間劃分

3.3 各指標基本概率分配

根據圖1,利用式(7)、(8)得出各指標各個等級的基本概率分配.由于指標過多,此處以日降雨量為例展示基本概率分配計算過程.①確定區間模型.根據表7,評價指標日降雨量區間數為[0,120]、[120,271]、[271,725]、[725,1500]mm.② 確定識別區間.通過現場監測得到萬花邊坡某一日的降雨量為29.6 mm,則日降雨量構成的識別區間為[-29.6,29.6]mm.③ 計算區間之間的距離.根據式(7)分別計算辨識框架下的4個區間模型與識別區間之間的距離,計算結果如表8所示.④ 計算區間之間的相似度.根據式(8)分別計算4個區間模型與識別區間之間的相似度,計算結果如表9所示.⑤ 將計算得到的相似度進行歸一化處理,得到各辨識框架下的基本概率分配,如表10所示.同理,可計算得到萬花邊坡其余基本評價指標在辨識框架下的基本概率賦值,計算結果如表11所示.

表8 四種狀態下2個區間之間的距離

表9 四種狀態下2個區間之間的相似度

表10 四種狀態下的基本概率賦值

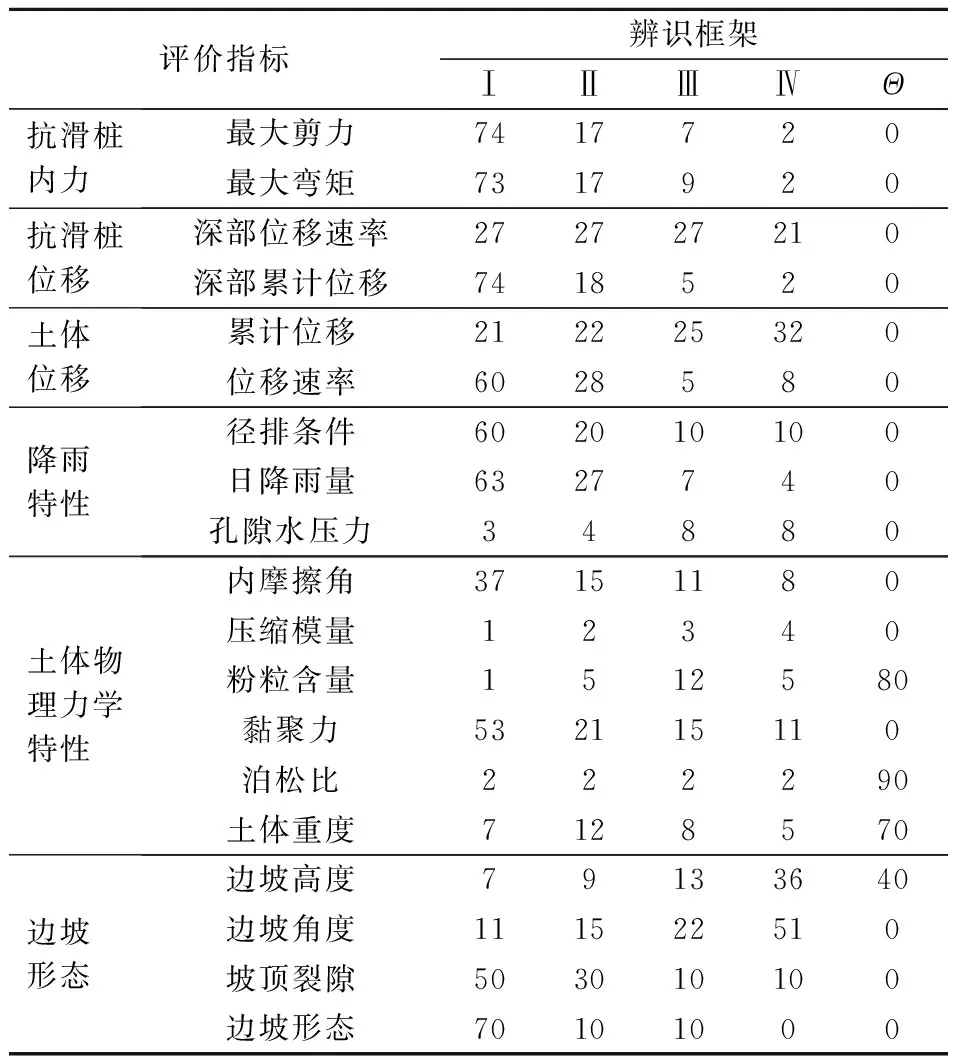
表11 考慮權重后各指標的基本概率賦值 %

3.4 計算各級指標置信度

采用式(10)計算下級指標作用下上級指標的可信度,計算結果如表12所示.

綜合上文基本概率賦值計算,根據相應證據推理的辨識框架,建立了支擋型黃土高陡邊坡的安全性評估可信度.從表12可以看出,目標邊坡的安全狀態和基本安全狀態的可靠性分別為73.25%和22.99%,因此可以假定該邊坡是安全的,與現場測試結果一致.

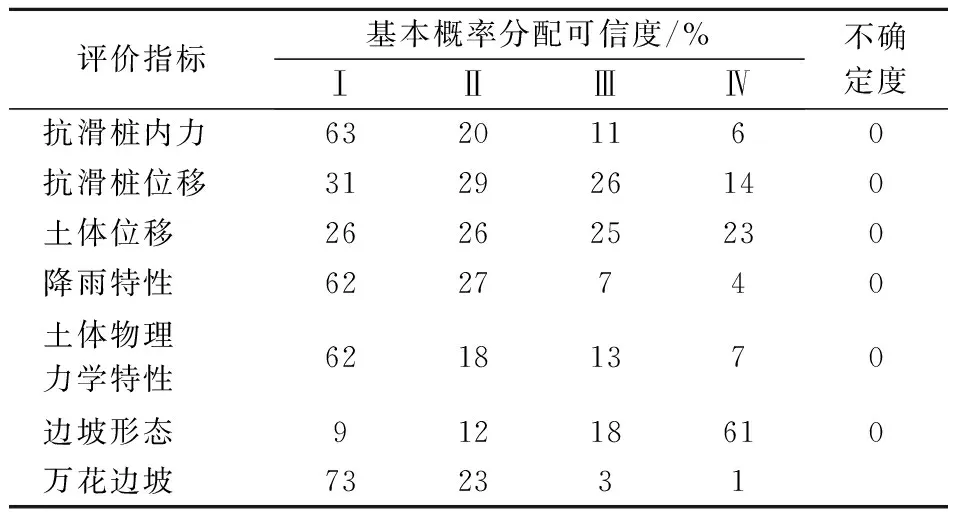
表12 萬花邊坡基本概率分配可信度

3.5 安全評價結果

各評價指標所占的權重是隨現場邊坡的實況而動態變化的,由此可對目標邊坡穩定性進行動態評估,0～800 d是連續監測的,為方便計算,每10 d取一組數據,利用Python編制計算程序,對其進行迭代運算.在4種穩定級別下,目標邊坡坡體及抗滑樁可靠性如圖4所示.從圖4(a)可看出,抗滑樁在基本安全狀態下的可靠度是逐步增加的,由此可以得出抗滑樁是安全的.從圖4(b)可看出,60 d時邊坡處于基本安全狀態的可信度超過了安全狀態的可信度,表明從此時起,邊坡的安全狀態已基本穩定,臨界的可信度逐步提高,520 d時坡體在臨界狀態下的可信度最高,表明土坡的安全狀況已達到一個危險的臨界狀態,并且正在逐漸地向破壞轉變.由圖4(c)知,目標邊坡的安全狀況與抗滑樁的可靠性是一致的,目前邊坡在安全狀態下的概率為73.31%,其安全狀況主要依賴于抗滑樁的安全狀況.

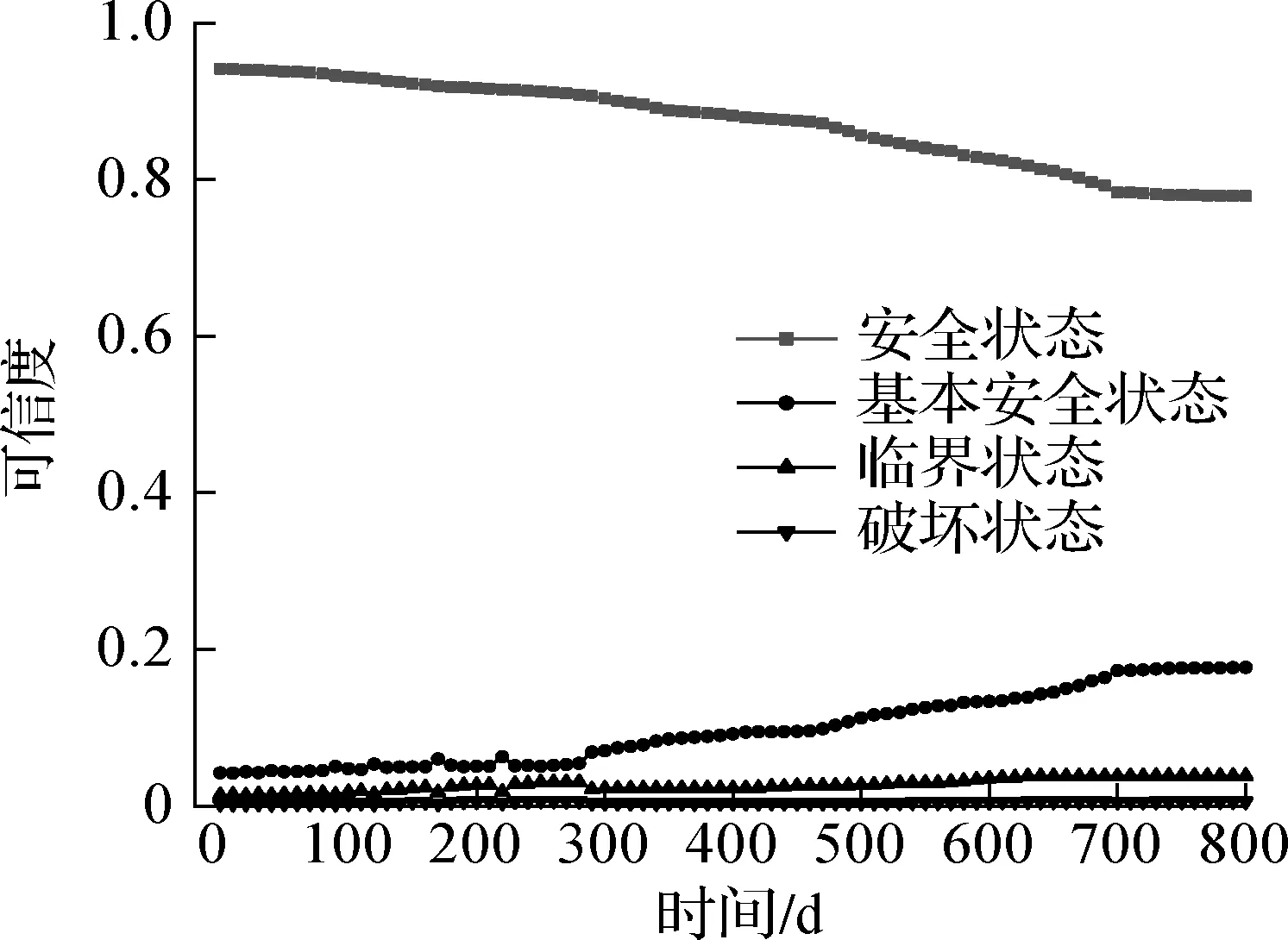
(a) 抗滑樁

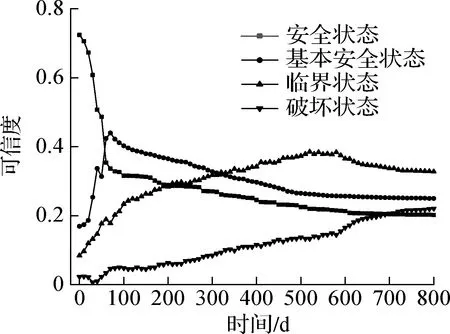
(b) 邊坡坡體

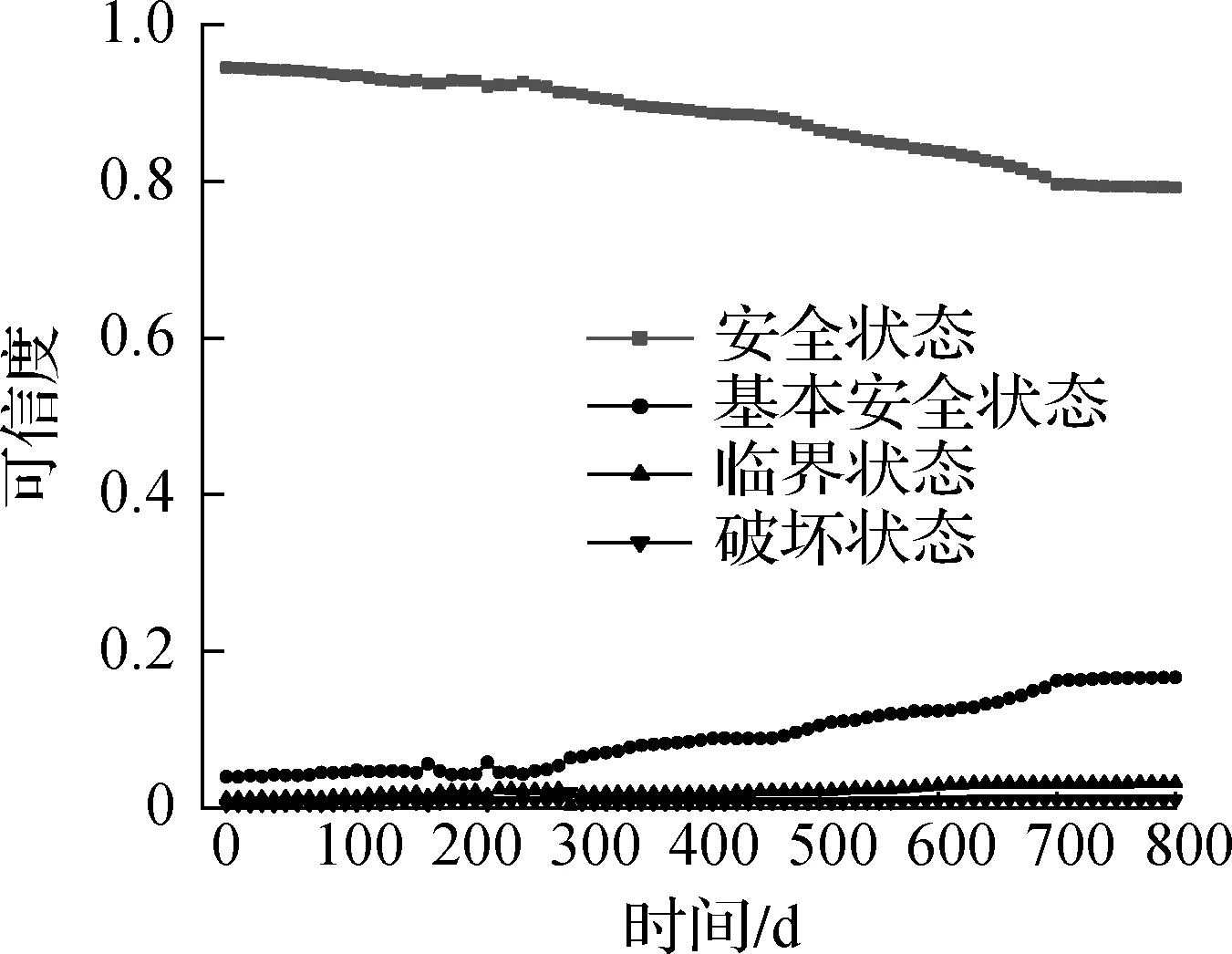
(c) 支擋型邊坡整體

邊坡動態指標如抗剪強度、降雨量、徑排條件、邊坡形態、邊坡坡度等在邊坡位移變化過程中的變化規律如圖5所示.由圖可知,邊坡的安全性變差主要是由于邊坡土體內部產生的剪應力達到了邊坡土體的抗剪強度;降雨對邊坡安全狀態的支持程度是隨降雨量而變化的,當有降雨產生時,基本指標降雨量對邊坡安全狀態的支持程度變小,當沒有降雨時,降雨量對邊坡安全狀態的支持程度較大;徑排條件、邊坡形態與邊坡坡度等指標對邊坡安全狀態的支持程度逐漸降低,并在降雨期間降低得更快.

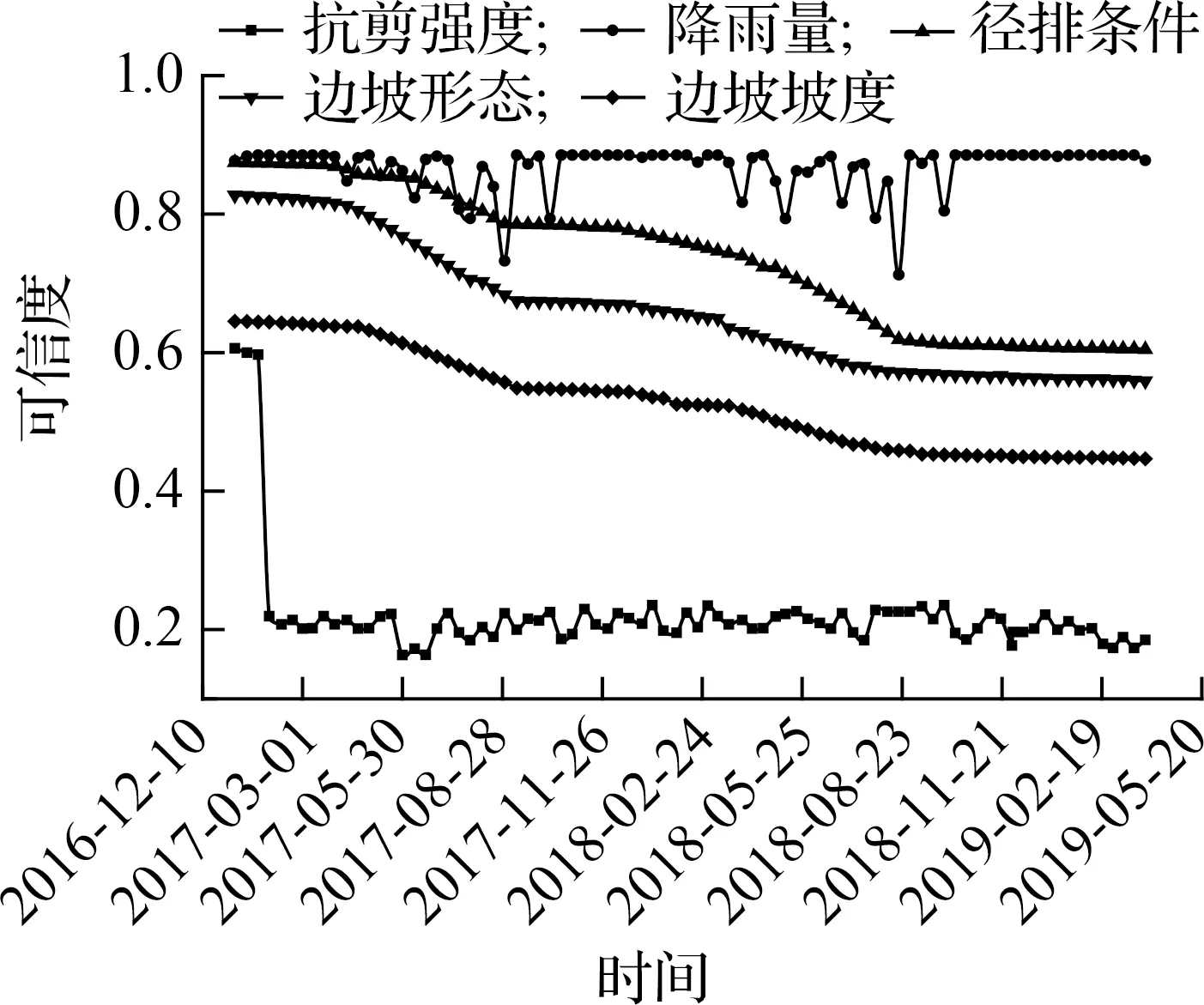
圖5 萬花邊坡動態指標變化規律

4 結論

1) D-S證據理論在邊坡穩定性評價的模糊性與不確定性中有優勢,可以很好地融合各個指標之間的不一致性,并對各個指標之間的一致性和沖突進行定量衡量,確保各指標能夠真實地反映高陡邊坡的特征,基于此提出一種支擋型黃土高陡邊坡穩定性評價方法.

2) 通過工程實例,對支擋型高陡黃土邊坡進行了安全性評估,證實基于證據理論評價的有效性和合理性.通用區間數法來構造基本概率分配的過程合理,且操作性強,計算得出的可信度高,評價結果精確.

3) 用證據理論對邊坡安全評價是可行的,且易于用程序實現,通過高陡邊坡水平位移推斷邊坡內部各指標,通過對坡體累積水平位移的現場監測數據推斷出抗滑樁的內力指標,從而推導出邊坡位移的動態參數.