寬速域翼尖渦及其與斜激波相互作用

馬印鍇，李祝飛，黃琪，楊基明

中國科學技術大學 近代力學系，合肥 230026

帶鴨翼的高馬赫數飛行器［1-3］憑借更大的升阻比、更好的操控性和更強的機動能力［4］，在寬速域飛行過程中展現出潛力。然而，鴨翼產生的翼尖渦往往威脅其下游部件的飛行安全［5-8］。特別是在高速飛行時，鴨翼產生的翼尖渦容易與激波發生相互作用，引起翼尖渦破碎和激波變形，進而可能導致翼/舵升力下降、阻力增大，甚至誘發進氣道不起動［9］等氣動問題。因此，探究翼尖渦的演化及其與激波的相互作用規律成為寬速域飛行中的重要課題之一。

低速不可壓縮來流中翼尖渦的研究幫助人們較早地意識到強翼尖渦對民航客機飛行安全的嚴重影響［10］。鑒于翼尖渦的強度與其切向速度和環量緊密相關［11］，認識這些參數的演化規律至關重要。1964年Batchelor［12］發現翼尖渦在不同流向站位處的切向速度剖面具有明顯的自相似性。隨后，Birch［13］、Beninati［14］和Ramaprian［15］等研究證實，翼尖渦的切向速度剖面符合Batchelor［12］提出的自相似關系式。進一步地，Grow［16］試驗研究發現，翼尖渦的環量和切向速度峰值都會隨著機翼展弦比和迎角的增大而增大。Mcalister和Takahashi［17］研究了來流雷諾數、機翼弦長等因素對翼尖渦環量分布和切向速度剖面的影響。Ramaprian和Zheng［18］發現翼尖渦的環量分布也存在自相似性，并給出了環量分布與翼尖渦半徑的關系式。最近，Skinner等［19］通過風洞試驗驗證了Ramaprian和Zheng［18］給出的環量自相似關系式。切向速度以及環量分布自相似規律的發現，極大地提升了人們對不可壓縮來流中翼尖渦的認知。

相對而言，超聲速/高超聲速來流中關于翼尖渦演化特性的研究非常有限。Smart等［20］在來流馬赫數Ma∞=2.49條件下，測量了翼尖渦內部的壓力分布和速度分布；Shevchenko等［21］在來流馬赫數Ma∞=6條件下，對比了翼尖渦內部不同流向位置處的壓力分布和溫度分布。然而，超聲速/高超聲速來流中的翼尖渦是否也具有自相似性，卻鮮見報道。

翼尖渦在激波作用下可能發生破碎，并導致飛行器性能驟降。已有的試驗和數值模擬研究［22-25］主要集中于來流馬赫數Ma∞=2～3，其結果表明，翼尖渦在激波作用下發生破碎時的主要特征包括激波面嚴重凸起變形、變形的激波下游存在亞聲速回流區、局部流動出現滯止［23-24］。針對正激波誘導翼尖渦破碎現象的理論研究相對較多［26-29］，例如，Delery等［30］于1984年較早地提出了一種預測渦破碎的理論判據；Mahesh［28］進一步擴展了該預測理論的適用范圍。然而，針對斜激波誘導翼尖渦破碎現象的理論研究卻很少。Hiejima［26］曾提出一種理論判據，但僅在Ma∞=2～3時進行了驗證。在寬速域飛行中，翼尖渦與斜激波相互作用將更加普遍，而現有的斜激波誘導翼尖渦破碎預測理論是否適用于寬速域，尚待進一步檢驗。

鑒于此，本文采用數值模擬方法，研究寬速域飛行過程中的翼尖渦演化特性及其與斜激波相互作用的規律，探討寬速域條件下斜激波誘導翼尖渦破碎的理論預測方法，以期為工程應用提供參考。

1 模型及數值模擬方法

1.1 鴨翼簡化構型

圖1為MR2.4試驗模型［31］。參考圖1所示LAPCAT Ⅱ高馬赫數飛行器MR2.4的鴨翼布局［31］，提煉鴨翼簡化構型用于產生翼尖渦。如圖2所示，該鴨翼構型呈直角梯形，展向截面為菱形，厚度為4 mm，根部弦長L=82 mm，寬度為75 mm，翼尖處的弦長為25 mm。以后緣根部頂點為坐標原點，定義流向為x方向，法向為y方向，展向為z方向。

圖1 MR2.4試驗模型［31］Fig.1 Test model of MR2.4［31］

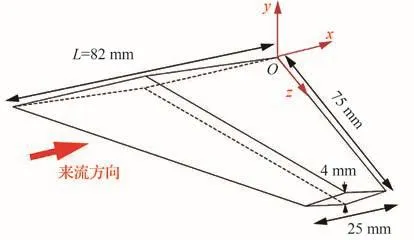
圖2 鴨翼簡化構型Fig.2 Simplified model of canard

為模擬寬速域飛行條件，本文參考Mehta等［3］的來流參數設置，以飛行高度30 km、來流馬赫數Ma∞=6為典型狀態點，通過保持來流動壓相等［32］，獲得了來流馬赫數Ma∞=0.2～6.0范圍的飛行條件，如表1所示。此外，考慮寬速域飛行器的迎角變化［3］，本文研究了迎角α= 6°，9°，12°對翼尖渦演化特性的影響。

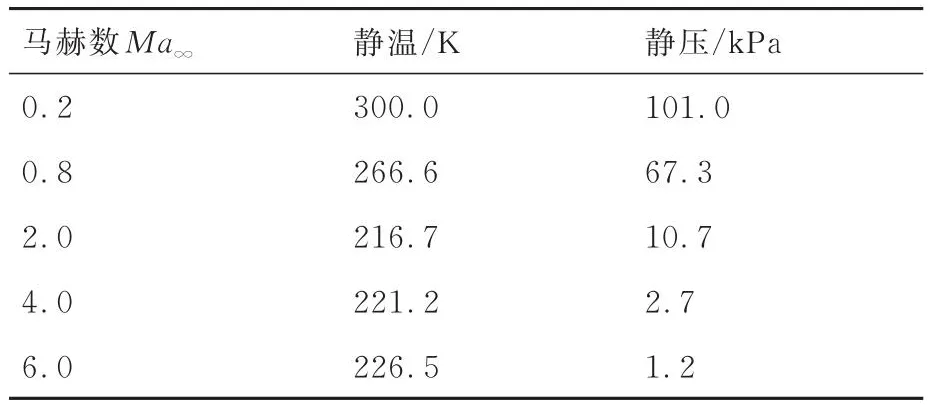
表1 模擬飛行條件Table 1 Simulated flight conditions

1.2 數值模擬方法

數值模擬采用雷諾平均的Navier-Stokes（RANS）方程求解器［33］，湍流模型采用k-ωSST（Shear Stress Transport）模型［34］，無黏通量采用Roe格式，對流項采用二階迎風格式，黏性項采用二階中心差分格式。空氣采用量熱完全氣體假設（比熱比γ=1.4），黏性系數采用Sutherland公式計算。

圖3為計算域及邊界條件，計算域采用六面體網格離散，來流參數設置與表1保持一致。鴨翼采用無滑移等溫固壁條件，壁溫為300 K，翼根處采用壓力遠場邊界條件以突出單個鴨翼的流場。下游出口采用壓力出口邊界，其余邊界均為壓力遠場條件。鑒于LAPCAT Ⅱ MR2.4飛行器［31］和SKYLON飛行器［3］的鴨翼與下游主翼之間的流向距離為3L～5L，將超聲速工況計算域（見圖3（a））的流向、法向和展向尺度分別設置為5.50L、1.46L和1.40L。如圖3（b）所示，為避免亞聲速擾動對翼尖渦造成影響，亞聲速工況計算域的流向、法向和展向尺度分別增大至35.5L、31.5L和31.4L。

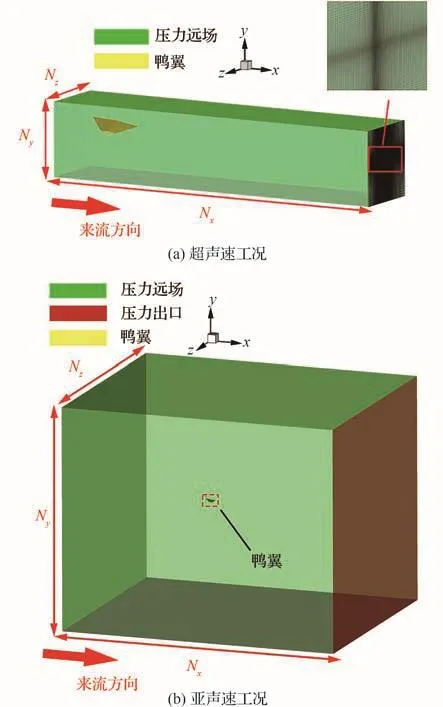
圖3 計算域和邊界條件設置Fig.3 Computational domain and boundary conditions setting

在超聲速/高超聲速來流條件下，翼尖渦與斜激波相互作用的示意圖如圖4所示，圖中β為激波角，具體參數見2.2節。在進行翼尖渦與斜激波相互作用的數值模擬時，在圖3（a）計算域的頂部邊界上，根據Rankine-Hugoniot關系式［32］分別給定入射斜激波上游和下游的氣流參數，則在圖4中的紅色虛線處將匹配出1道入射斜激波。若保持該入射斜激波的強度不變，通過設置邊界條件，沿流向移動該斜激波的入射位置，可使其與不同強度的翼尖渦發生相互作用。

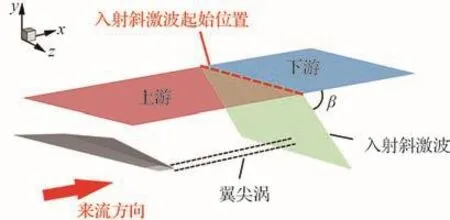
圖4 翼尖渦與斜激波相互作用示意圖Fig.4 Schematic of wingtip vortex/oblique shock wave interaction

表2為超聲速工況采用的3套網格。如表2所示，以超聲速工況為例，采用3套不同分辨率的網格考核了網格無關性，其中，Nx、Ny和Nz分別表示計算域流向、法向和展向的網格點數。為精細刻畫翼尖渦結構，針對鴨翼及其下游流場附近的網格進行了局部加密，壁面y+＜1，3套網格的總網格量分別約為1.8×107、3.5×107和5.2×107。

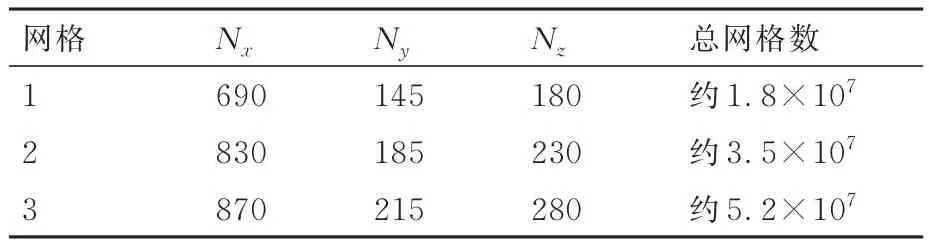
表2 超聲速工況采用的3套網格Table 2 Three sets of grids used in supersonic flow

如圖5所示，以來流馬赫數Ma∞=2鴨翼下游無量綱流向站位x/L=2為例，提取了不同網格得到的當地翼尖渦內部靜壓分布曲線，其中，Ps為翼尖渦內部靜壓，P∞為來流靜壓，y/L為法向無量綱坐標。通過對比可以發現，由網格2和網格3得到的壓力曲線基本重合。為提升計算效率，后續采用網格2對超聲速工況進行數值模擬和流場分析。此外，針對亞聲速工況，在網格2的基礎上分別沿流向、法向和展向擴大計算域尺度（如圖3（b）所示），其網格點分布如表3所示。

表3 亞聲速工況采用的網格分布Table 3 Grid used in subsonic flow

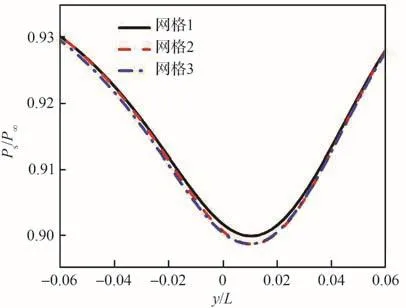
圖5 不同分辨率網格得到的壓力曲線對比Fig.5 Comparison of pressure curves obtained by grids of different resolutions

為驗證本文數值模擬方法對翼尖渦的刻畫能力，采用Beresh等［35］在來流馬赫數Ma∞=0.8、迎角α=10°條件下，通過試驗得到的模型尾緣下游4.18倍弦長處的翼尖渦切向速度剖面，對數值模擬方法進行了考核。如圖6所示，橫坐標z/L為展向無量綱坐標，縱坐標為無量綱切向速度。對比切向速度Uθ的試驗結果（圖6中U∞為來流速度）和數值模擬結果可以看出，兩者良好符合，表明本文采用的數值模擬方法能夠可靠地刻畫亞聲速流動中的翼尖渦。

圖6 亞聲速流動中的數值模擬結果與試驗結果對比Fig.6 Comparison between numerical and experimental data in subsonic flow

采用Smart等［20］在來流馬赫數Ma∞=2.49、迎角α=10.4°條件下，通過試驗測得的模型尾緣下游2.25倍弦長處的翼尖渦內部無量綱切向速度Mθ，考察了本文數值模擬方法對超聲速流動中翼尖渦的刻畫能力。圖7為超聲速流動中的數值模擬結果與試驗結果對比，由圖7可以發現，數值模擬結果與試驗結果良好符合。此外，筆者前期研究工作［36-37］也表明所采用的數值模擬方法對旋渦結構的刻畫是可靠的。

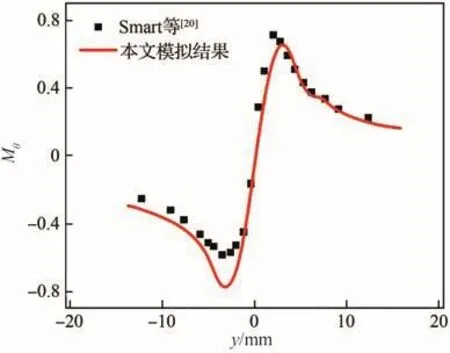
圖7 超聲速流動中的數值模擬結果與試驗結果對比Fig.7 Comparison between numerical and experimental data in supersonic flow

采用Smart和Kalkhoran［23］在來流馬赫數Ma∞=2.5條件下，利用29°斜劈進行的流向渦與斜激波相互作用試驗，檢驗了本文數值模擬方法對翼尖渦與斜激波相互作用現象的刻畫能力。圖8為激波凸起程度的試驗結果與數值結果對比。由圖8可知，采用流向密度梯度云圖（圖8（b））顯示的激波凸起位置僅比試驗結果（圖8（a））偏大約5%，表明本文數值模擬方法的可靠性良好。

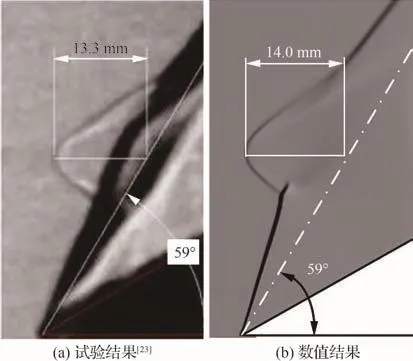
圖8 流向渦與斜激波相互作用的試驗結果與數值結果對比Fig.8 Comparison of experimental and present numerical results of interaction between streamwise vortex and oblique shock wave

2 結果與討論

2.1 寬速域翼尖渦演化特性

以來流馬赫數Ma∞=6典型狀態為例，圖9采用流向渦量等值面顯示了翼尖渦的三維結構，并以紅色箭頭標注了其旋轉方向。本節以翼尖渦的切向速度剖面和環量分布為關鍵參數，分析寬速域翼尖渦的演化特性。

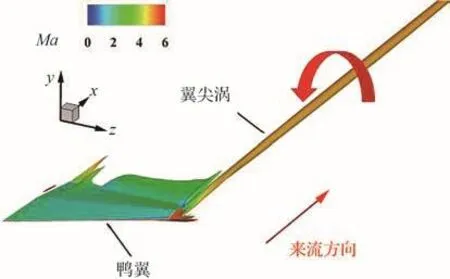
圖9 翼尖渦三維結構（流向渦量等值面）Fig.9 Three-dimensional structure of wingtip vortex（iso-surface of streamwise vorticity）

2.1.1 翼尖渦的切向速度分布

圖10為來流馬赫數Ma∞=0.2～6.0、迎角α=6°時，流向站位x/L=1～5處翼尖渦的切向速度剖面。鑒于同一來流馬赫數下不同流向站位的切向速度分布規律幾乎一致，圖10采用相同的圖例表示不同流向站位，下文均采用這種簡潔的標注方式。圖10中：Uθ（r）為翼尖渦內部徑向坐標r處的切向速度；Uθ，max為切向速度峰值；rc為翼尖渦的半徑，通常取Uθ，max所在的徑向坐標［35］。從圖10可以看出，在低速至高超聲速的寬速域范圍內，不同流向站位的翼尖渦切向速度剖面均呈現明顯的自相似性。作為對比，在圖10中還畫出了低速不可壓縮流動中翼尖渦切向速度剖面的Batchelor［12］自相似關系式，其表達式為

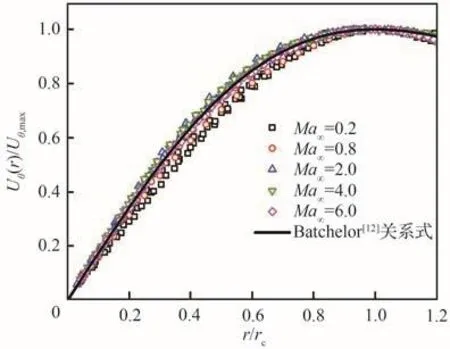
圖10 不同來流條件下的切向速度剖面Fig.10 Tangential velocity profiles at various flow conditions

式中：b=1.256 43為Lamb常數［38］。圖10中的數據均與式（1）良好符合，表明超聲速/高超聲速流動中的翼尖渦同樣遵循式（1）。

圖11以來流馬赫數Ma∞=6為例，在不同流向站位處（x/L=1～5）對比了迎角α對翼尖渦切向速度剖面的影響。可以看出，迎角變化對翼尖渦切向速度自相似性的影響可以忽略。

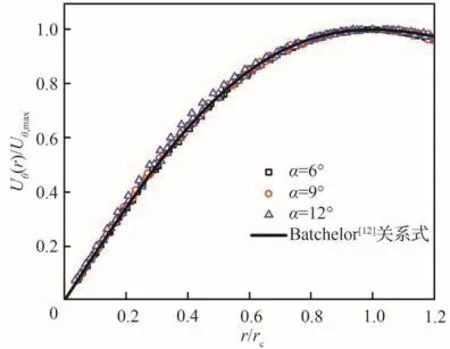
圖11 Ma∞=6.0不同迎角的切向速度剖面Fig.11 Tangential velocity profiles at Ma∞=6.0 with different angles of attack

2.1.2 翼尖渦的環量分布

當0＜r/rc＜1.2時，Skinner等［19］通過試驗發現低速不可壓縮流動中的翼尖渦在不同流向站位處的環量Γ也具有自相似性，并通過擬合得

式中：Γ為翼尖渦內部徑向坐標r處的環量；Γc為翼尖渦半徑rc處的環量。

事實上，根據式（1）的翼尖渦切向速度剖面，也能夠獲得環量分布。由式（1）獲得的環量分布曲線［12］與式（2）［19］的對比如圖12所示，可以看出，兩者的環量分布曲線幾乎重合。

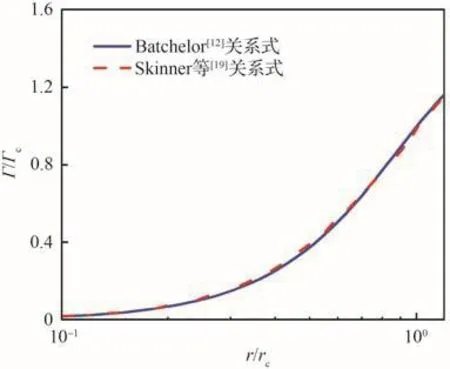
圖12 環量分布曲線對比Fig.12 Comparison of circulation profiles

為檢驗式（2）是否適用于超聲速/高超聲速流動中的翼尖渦，圖13給出了來流馬赫數Ma∞=0.2 ～6.0范圍、迎角α=6°時，流向站位x/L=1～5處翼尖渦的環量分布，并與式（2）的曲線進行了對比。可以看出，超聲速/高超聲速流動中翼尖渦的環量分布與式（2）均良好吻合。這表明式（2）可推廣至寬速域，極大地拓展了式（2）的適用范圍。

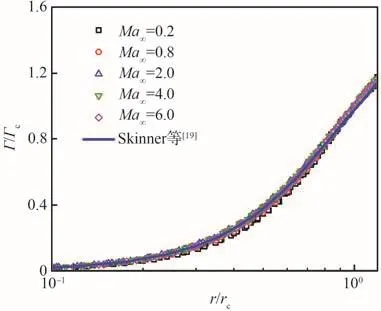
圖13 不同來流條件下的環量分布曲線Fig.13 Circulation profiles at various flow conditions

圖14以來流馬赫數Ma∞=6.0為例，考察了不同流向站位處（x/L=1～5）迎角α對于翼尖渦環量分布自相似性的影響。從圖14可以看出，不同迎角下的環量分布曲線幾乎重合，表明迎角α不會改變翼尖渦環量分布的自相似性。

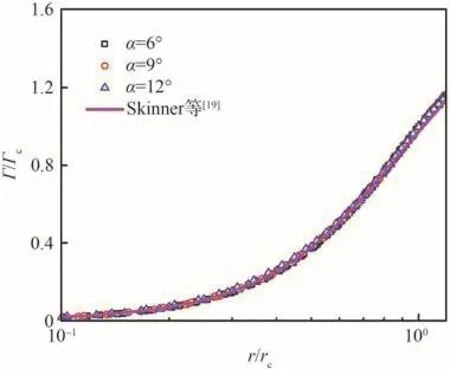
圖14 Ma∞= 6.0條件下不同迎角的環量分布曲線Fig.14 Circulation profiles at Ma∞=6.0 with different angles of attack

2.1.3 翼尖渦旋流數

為描述寬速域條件下翼尖渦沿流向的演化，采用文獻［28］定義的旋流數τ=Uθ，max/U∞衡量翼尖渦的強度。圖15為來流馬赫數Ma∞=0.2～6.0、迎角α=6°時，旋流數τ沿流向的變化曲線。可以看出，當來流馬赫數較低時（Ma∞= 0.2，0.8），τ沿流向的變化較小，表明翼尖渦的強度相對穩定；當來流為超聲速至高超聲速時（Ma∞=2.0～6.0），τ沿流向迅速減小。寬速域條件下旋流數τ沿流向的變化趨勢表明，當飛行器逐漸加速至高超聲速時，翼尖渦強度沿流向的減弱趨勢將更加明顯，其對下游部件的影響也將相應地減弱。

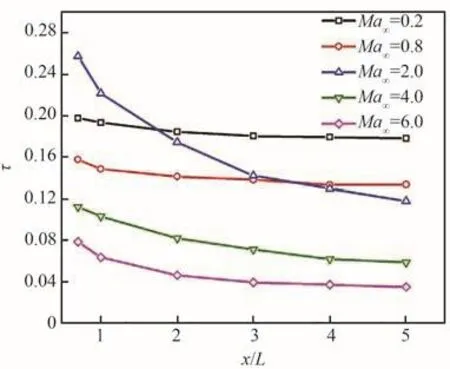
圖15 不同Ma∞下旋流數沿流向變化（α=6°）Fig.15 Variations of swirl number along streamwise direction at different Ma∞ （α=6°）

圖16以來流馬赫數Ma∞=6.0為例，對比了不同迎角α時旋流數τ沿流向的變化。可以看出，迎角α越大，翼尖渦越強。因此，在超聲速和高超聲速流動中，應重視大迎角情況下翼尖渦與激波的干擾問題。

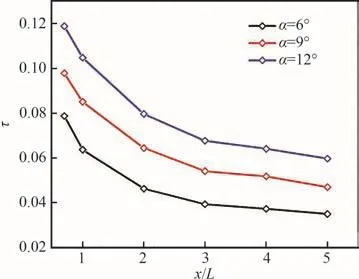
圖16 不同迎角下旋流數沿流向變化（Ma∞=6.0）Fig.16 Variations of swirl number along srteamwise direction at different angles of attack（Ma∞=6.0）

2.2 翼尖渦與斜激波相互作用

表4～表6對比了來流馬赫數Ma∞=2，4，6和迎角α=12°時，翼尖渦在典型流向站位處的參數。其中：P1，c/P1，∞表征翼尖渦的壓力虧損（P1，c為斜激波上游渦核處的靜壓，P1，∞為斜激波上游的來流靜壓）；U1，c/U1，∞表征翼尖渦的速度虧損（U1，c為斜激波上游渦核處的速度，U1，∞為斜激波上游的來流速度）。

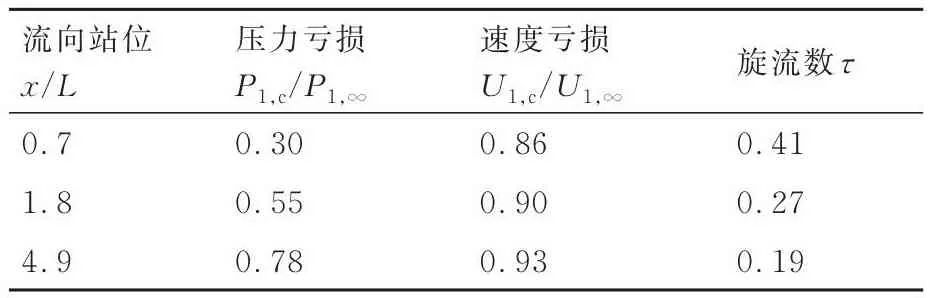
表4 Ma∞=2典型流向站位處翼尖渦的物理參數Table 4 Physical parameters of wingtip vortex at typical locations in Ma∞=2 flow

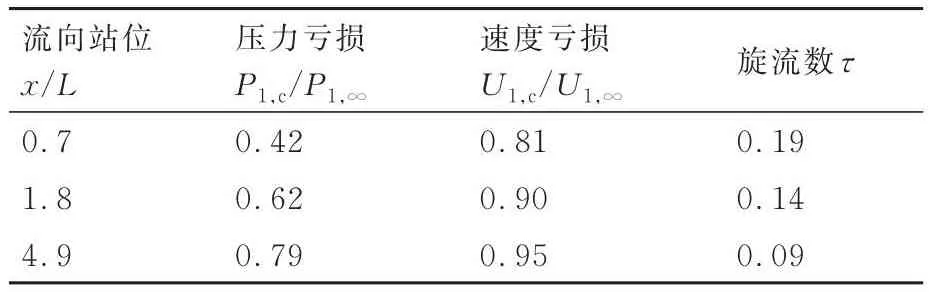
表5 Ma∞=4典型流向站位處翼尖渦的物理參數Table 5 Physical parameters of wingtip vortex at typical locations in Ma∞=4 flow

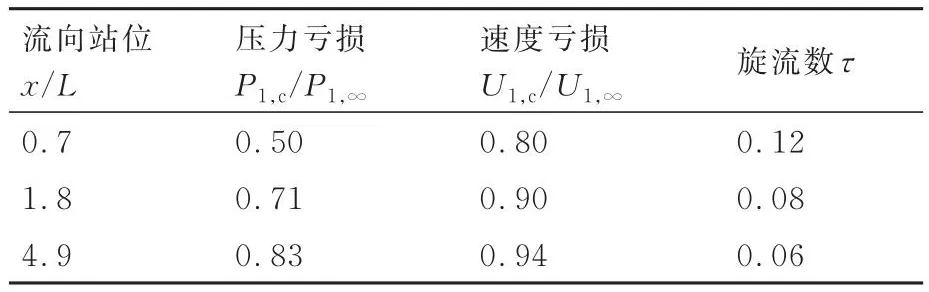
表6 Ma∞=6典型流向站位處翼尖渦的物理參數Table 6 Physical parameters of wingtip vortex at typical locations in Ma∞=6 flow

從表4～表6可知，隨著翼尖渦沿流向發展，其旋流數τ逐漸減弱，而P1，c/P1，∞和U1，c/U1，∞均逐漸增大，特別是P1，c/P1，∞的變化幅度更劇烈。這表明P1，c/P1，∞很可能會影響翼尖渦與斜激波的相互作用。鑒于在斜激波強度不變時，翼尖渦越強，越有可能發生渦破碎［23］。本節選取迎角α=12°工況，旨在暴露寬速域飛行過程中可能遇到的強翼尖渦情況。在來流馬赫數Ma∞=2，4，6和入射斜激波的激波角β分別為60°、63°和55°工況下，分析斜激波誘導的翼尖渦破碎流場和翼尖渦不破碎流場的典型特征。

2.2.1 翼尖渦破碎流場

以來流馬赫數Ma∞=2工況為例，圖17為激波角β=60°、流向站位x/L=0.7處，翼尖渦與斜激波相互作用時的典型三維結構，其中，激波采用壓力等值面顯示，以有效地將其與剪切層、滑移線等流動現象相區分［39］；翼尖渦采用流向渦量等值面顯示。從圖17（a）可以看出，激波面在翼尖渦核軸線附近的凸起程度最劇烈，呈現為局部錐形凸起。為展示凸起激波面下游翼尖渦的變化，按照圖17（a）中黑色箭頭所示的方向，圖17（b）進一步展示了下游三維流場結構。從圖17（b）可以看出，翼尖渦在凸起激波面下游基本消失，表明翼尖渦與斜激波相互作用后發生了破碎。

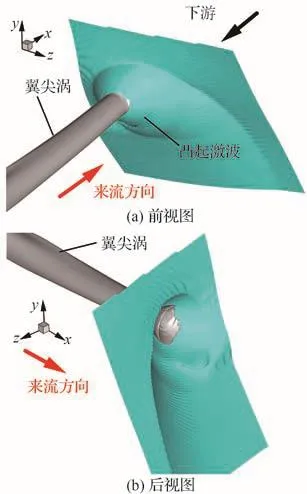
圖17 渦破碎典型三維流場Fig.17 Typical three-dimensional flowfield of vortex breakdown

圖18為來流馬赫數Ma∞= 2，4，6條件下，翼尖渦與斜激波相互作用流場中x/L=0.7站位處渦核軸線所在z截面的馬赫數云圖。可以看出，凸起激波的最前緣均出現在渦核軸線附近，且接近于1道正激波；凸起激波的下游均存在流動滯止點和大范圍的亞聲速區，并伴隨明顯的局部回流現象。這些特征，再次證實翼尖渦發生了破碎。

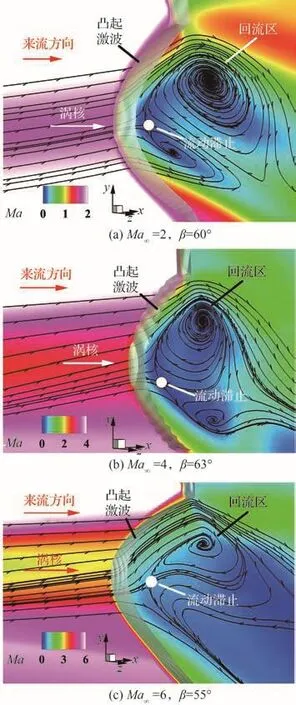
圖18 渦破碎流場中渦核軸線截面馬赫數云圖Fig.18 Streamlines superimposed on Mach number contours near vortex core of vortex breakdown

2.2.2 翼尖渦不破碎流場

以來流馬赫數Ma∞=2工況為例，圖19為激波角β=60°、流向站位為x/L=4.9處，翼尖渦與斜激波相互作用的典型三維流場。其中，激波面、翼尖渦分別采用壓力等值面、流向渦量等值面顯示。從圖19（a）可以看出，激波面在渦核軸線附近僅發生輕微凸起。圖19（b）進一步展示了激波面下游的三維流場結構，可以看出，在斜激波下游翼尖渦并未消失，而是隨波后氣流向下偏轉并繼續向下游發展。這表明翼尖渦與斜激波相互作用后，未發生破碎。

圖19 渦不破碎三維流場Fig.19 Three-dimensional flowfield of vortex nonbreakdown

圖20為來流馬赫數Ma∞=2，4，6條件下，翼尖渦與斜激波相互作用流場中x/L=4.9站位處渦核軸線所在z截面的馬赫數云圖。可以看出，激波面的凸起程度較小，波后雖然存在明顯的亞聲速區，但并未出現回流或流動滯止現象。這些特征再次證實翼尖渦沒有破碎。

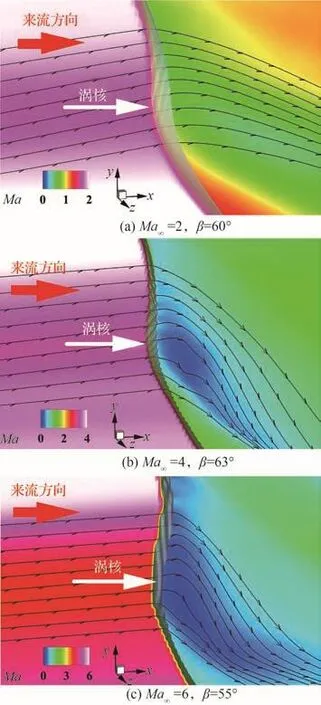
圖20 渦不破碎流場中渦核軸線馬赫數云圖Fig.20 Streamlines superimposed on Mach number contours near vortex core of vortex non-breakdown

2.3 斜激波誘導翼尖渦破碎預測理論

在來流馬赫數Ma∞=2～6范圍內，翼尖渦與斜激波相互作用后，均有可能發生破碎（見2.2節）。現有理論［26-29］能否準確預測寬速域中斜激波誘導的翼尖渦破碎現象，是值得探討的重要問題。

2.3.1 Mahesh預測理論

根據Mahesh［28］對翼尖渦與正激波相互作用問題的研究，翼尖渦發生破碎需滿足：

式中：P為靜壓；ρ為密度；U為速度；1和2分別表示激波上游和下游；∞和c分別表示自由來流和渦核。在不考慮翼尖渦內部速度虧損的前提下，Mahesh［28］認為翼尖渦渦核與激波相互作用后所經歷的最大壓差為P2，∞-P1，c，當該壓差大于其在激波前的動量通量ρ1，cU21，c時，渦核處的氣流將在激波后出現局部流動滯止，進而導致翼尖渦發生破碎。所以式（3）兩邊取等號時，即為翼尖渦發生破碎的臨界條件。

為便于對渦破碎進行理論預測，Mahesh［28］假設旋渦內部總溫均勻分布，根據上述臨界條件推導了翼尖渦恰好發生破碎時的臨界旋流數τcri與自由來流馬赫數Ma1，∞以及入射斜激波的激波角β之間的關系式為

需要注意的是，Mahesh［28］并未對式（4）能否準確預測斜激波誘導渦破碎現象進行檢驗。若事先已知自由來流馬赫數Ma1，∞和入射斜激波的激波角β，則可以得到臨界旋流數τcri。將翼尖渦的旋流數τ與臨界旋流數τcri進行比較，若τ＞τcri，翼尖渦將會發生破碎。

為考察Mahesh［28］理論預測的準確性，本文在來流馬赫數Ma∞=2，4，6條件下，對翼尖渦與斜激波相互作用現象進行了數值模擬，入射翼尖渦位置的變化范圍為x/L=0.7～4.9（見表4～表6）。其中，Ma∞=2時，斜激波激波角的變化范圍為β=37°～60°；Ma∞=4和6時，斜激波激波角的變化范圍為β=30°～63°。本文數值模擬翼尖渦是否破碎的結果與Mahesh［28］預測理論式（4）的對比如圖21所示。圖中黑色實線表示式（4），該實線上方的區域表示發生渦破碎；該實線下方的區域表示不發生渦破碎。可以看出，Mahesh［28］理論的預測結果傾向于翼尖渦更容易破碎，這與本文的數值模擬結果不完全符合，表明該理論存在局限性。

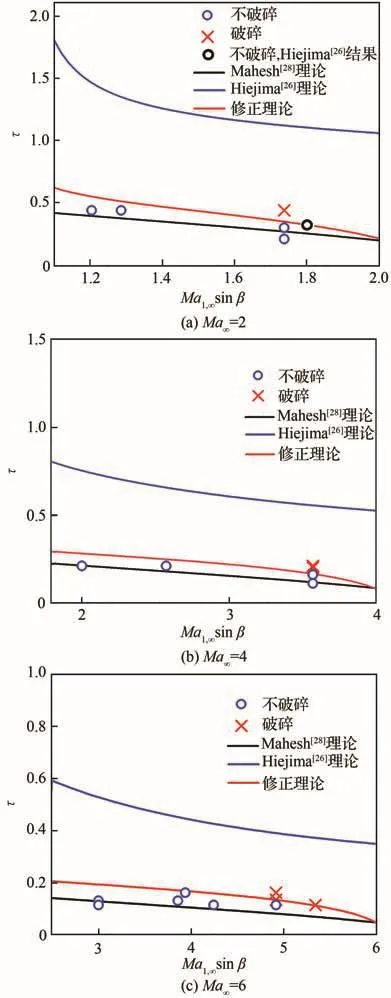
圖21 渦破碎理論預測Fig.21 Theoretical prediction of vortex breakdown

2.3.2 Hiejima預測理論

根據Hiejima［26］對斜激波誘導翼尖渦破碎問題的研究，翼尖渦發生渦破碎至少需要滿足式（5）或式（6）之一。

式中：Maθ=Uθ，max/s，s為當地聲速。假定翼尖渦與斜激波無相互作用，則來流和渦核處氣流跨過斜激波產生的壓差分別為P2，∞-P1，∞和P2，c-P1，c。根據式（5）可知，當兩者之間的差量ΔP大于斜激波下游氣流的動壓（U2，∞為斜激波下游氣流速度）時，翼尖渦將發生破碎。根據式（6）可知，若翼尖渦與斜激波相互作用前Maθ＞1，則翼尖渦會發生破碎。所以，翼尖渦發生破碎的臨界條件分別為

事先通過數值模擬容易得到無斜激波入射時當地翼尖渦的Maθ。在本文來流馬赫數Ma∞=2～6范圍內的翼尖渦（見表4～表6），其Maθ始終＜1，均不滿足式（6）。因此，本文主要關注式（5） 能否準確預測渦破碎。

為便于使用Hiejima［26］預測理論以及與Mahesh［28］理論（見2.3.1節）進行對比，本文參考Mahesh［28］的推導過程，將式（10）轉化為τcri與Ma1，∞、β之間的關系式。首先，采用P1，∞對式（10）兩邊做無量綱化，整理可得

然后，根據Mahesh［28］的假設，認為旋渦內部總溫均勻分布，得到P1，c/P1，∞與τcri的關系式為［28］

最后，在不考慮翼尖渦內部速度虧損的前提下，根據Rankine-Hugoniot關系式［32］，可得

再結合式（13），將式（12）轉化為

式（16）可表示為圖21中的藍色實線，該實線上方的區域表示翼尖渦發生破碎；該實線下方的區域表示翼尖渦不破碎。從圖21可以看出，Hiejima［26］理論式（16）的預測結果傾向于不發生渦破碎，這與本文的數值模擬結果不相符；同時，也表明在寬速域范圍，該理論難以準確預測斜激波誘導的翼尖渦是否會發生破碎。

2.3.3 修正的預測理論

由上述分析可知，Mahesh［28］理論和Hiejima［26］理論均難以在寬速域范圍準確預測斜激波誘導的翼尖渦破碎現象。結合2.2節的分析以及表4～表6可以看出，當來流馬赫數和入射斜激波強度保持不變時，翼尖渦渦核處的壓力虧損越劇烈，則翼尖渦越容易發生破碎。然而，Mahesh［28］理論和Hiejima［26］理論均未考慮壓力虧損的影響，因此，有必要對其進行修正。鑒于Hiejima［26］理論本身就是針對斜激波誘導翼尖渦破碎問題而提出的，因此在其基礎上恰當地引入壓力虧損的影響，進一步挖掘潛力，很有可能獲得更加準確的預測理論。

本文采用翼尖渦壓力虧損值P1，c/P1，∞修正Hiejima［26］理論式（5）的左端項，修正后的預測理論為

當式（17）成立時，翼尖渦將發生渦破碎；反之，則翼尖渦不破碎。換言之，式（17）取等號時，即為修正后翼尖渦發生破碎的臨界條件。式（17）兩邊取等號后，再同時除以P1，∞進行無量綱化，整理可得

為便于使用修正后的預測理論，采用與

2.3.2 節相同的推導思路，將式（18）轉化為

類似地，可將式（19）表示為圖21中的紅色實線，該實線上方為翼尖渦發生破碎的區域，下方為翼尖渦不破碎的區域。從圖21可以看出，在寬速域范圍，修正理論的預測結果與本文的數值模擬結果均良好吻合。可見，考慮翼尖渦壓力虧損的影響，并用于修正Hiejima［26］原有的預測理論，能夠大幅提升其對斜激波作用下翼尖渦是否破碎的預測能力。這一發現，對于掌握翼尖渦與斜激波相互作用的規律，具有重要價值。

3 結論

本文在寬速域范圍研究了翼尖渦的演化特性，分析了翼尖渦與斜激波相互作用的流場，并探討了斜激波誘導翼尖渦破碎的預測理論，主要得到以下結論：

1）在寬速域范圍（來流馬赫數Ma∞=0.2～6.0），翼尖渦不同流向站位的切向速度剖面和環量分布仍然遵循低速流動中的自相似規律，并且迎角對這種自相似性的影響可以忽略。

2）相比于亞聲速來流，在超聲速來流中翼尖渦強度沿流向減弱地更快；隨著迎角增大，翼尖渦增強，但其強度沿流向的減弱速度變化不明顯。

3）通過引入渦核處壓力虧損的影響，對現有斜激波誘導翼尖渦破碎理論進行修正，大幅提升了其在來流馬赫數2～6范圍內預測渦破碎的能力。

鑒于斜激波誘導翼尖渦破碎現象的復雜性，未來需在寬速域范圍，尤其是高馬赫數來流中，開展精細的試驗研究。