基于新型粒子群算法的結構動力學熱振模型修正

王震宇，王計真，楊婧藝，何鵬遠，潘成浩，周凌波，何成，何歡，*

1.南京航空航天大學 機械結構力學及控制國家重點實驗室，南京 210016

2.南京航空航天大學 振動工程研究所，南京 210016

3.中國飛機強度研究所 結構沖擊動力學航空科技重點實驗室，西安 710065

4.中國船舶科學研究中心 船舶振動噪聲重點實驗室，無錫 214082

5.南京航空航天大學 無人機研究院，南京 210016

高速飛行器需要在熱、聲和機械載荷等極端組合環境中長時巡航，無法正確考慮環境/載荷、結構響應和不斷變化的材料狀態之間的非線性耦合是當前預測系統響應和結構壽命的主要問題［1］。高溫環境對于結構振動特性的影響主要有2方面：一方面，由于材料參數隨溫度改變，結構本身的剛度也會隨著溫度的升高而降低；另一方面，結構在高溫下不可避免地會在內部產生一定的熱應力，因而附加的初始應力剛度矩陣會改變結構的整體剛度［2-3］。大型復雜結構通常由多組件連接構成。連接結構存在應力集中、幾何或邊界非線性、預緊力和摩擦等不確定因素，且在熱環境下連接狀態會隨著線脹現象、材料軟化及間隙狀態等變化而變化［4］。有限元模型為理解高溫環境下復雜多組件飛行器結構在各種載荷條件下的性能提供了一種方便的方法，減少動力學有限元模型的誤差是成功預示結構振動響應的關鍵。模型修正作為利用較為準確的實驗結果減少有限元模型計算誤差的有效技術，已經廣泛應用于航空、航天、建筑等領域。有限元模型修正方法依據修正對象的不同可分為直接修正方法和迭代修正方法［5-6］。隨著計算機技術的發展，迭代修正方法因其物理意義明確、便于結合大型工程軟件等優點逐漸成為主流方法。迭代修正方法的基本思路與結構優化理論相似，需要對復雜的非線性罰函數進行最小化處理［7］。

近幾十年來，許多智能算法的出現極大地提高了迭代修正的效率和精度。張安平等［8］提出一種基于混合人工魚群算法（HAFSA）的修正方法，并以GARTEURE飛機模型為例證明了該方法的可行性。He等［9］結合徑向基函數（RBF）代理模型和非支配排序遺傳算法（NSGA-Ⅱ）使用模型修正的方法實現了針對不同溫度分布系統的熱物性參數辨識。Tran-Ngoc等［10］基于正交對角化改進粒子群算法（IPSO）并應用到大型鐵路橋梁模型修正中，顯著降低了迭代計算成本。于開平和劉榮賀［11］提出一種多族群粒子群優化算法（MRPSO），降低了搜索陷入局部最優的概率，并將該算法成功引入模型飛行器的模型修正問題中。Yin和Zhu［12］介紹了貝葉斯神經網絡（BNN）架構在模型修正中的一般設計方法，并通過對人行天橋的有限元模型修正證明了該算法的有效性。

粒子群優化算法（PSO）是一種模擬鳥群覓食行為的元啟發式算法，在實際工程中得到越來越廣泛的應用［13］。針對粒子群算法早熟收斂和易陷入局部最優等缺點的改進工作可以分為3個方向：①引入或優化超參數。例如，Shi和Eberhart［14-15］依次引入慣性權重和收縮因子，并比較了這2種時變參數的性能。Chatterjee和Siarry［16］在粒子群算法中使用自適應非線性變化的慣性權重，使得該算法可以在初期迭代中粗調，快速接近最優解，并在后續迭代中逐漸精調，更精確地逼近最優解。②改進粒子種群的拓撲結構和搜索策略，Al-Bahrani和Patra［17］根據適應度值將粒子群分為活性組和惰性組，采用正交對角化來替代原有的粒子更新策略，極大地提高算法的精度和速度。Zhan和Zhang［18］通過田口方法構造出新的粒子進行引導，避免了2種歷史經驗之間的沖突。③與其他優化算法進行融合，優勢互補。Zhao等［19］將和聲搜索（HS）與PSO融合為一種新的優化算法，并通過馬爾可夫模型分析了其收斂性能。Zhang等［20］結合灰狼優化算法（GWO）和IPSO，得到一種混合算法。通過K-均值聚類優化實驗表明該算法具有較好的優化性能和較強的通用性。

萊維飛行（Lévy Flight）是服從萊維分布（Lévy Distribution）的隨機游走，其步長具有重尾分布的特點［21］。自然界中如黃蜂、馴鹿等許多生物的最佳覓食軌跡都滿足萊維飛行。萊維飛行已廣泛應用于布谷鳥算法（CS）等全局優化算法中［22］。在粒子群中，假設部分粒子有一定的概率失去先驗的最優位置信息，此時粒子的搜索策略類似于生物覓食的隨機游走行為。萊維飛行可以增強粒子群算法的全局搜索能力，Hakli和H?uz［21］融合萊維飛行提出LFPSO算法，并在多個基準函數上證明LFPSO算法比遺傳算法（GA）、差分進化算法（DE）、人工蟻群算法（ABC）以及其他粒子群變體算法搜索能力更強。在此基礎上，Jensi和Jiji［23］提出的PSOLF算法在21個基準函數上的測試表現均優于標準粒子群算法、LFPSO等其他改進粒子群算法，但PSOLF算法依然沒能避免傳統算法中局部和全局2種引導經驗之間的沖突［24］，在搜索具有多個局部最優峰值的高維復雜函數時，仍然不能得到理論最優解。

本文針對高溫環境復雜結構動力學問題輸入輸出關系復雜、多狀態性、不確定性等有別于傳統動力學問題的特點，提出一種基于田口試驗設計和萊維飛行的新型粒子群算法——萊維正交粒子群算法（LOPSO），并應用于高溫環境典型復雜多組件結構模型修正問題中。為了驗證LOPSO算法的搜索能力，本文以軸系軸承-軸承座彈簧阻尼參數修正問題為例，與性能優異的PSOLF算法進行對比，驗證LOPSO算法具的搜索能力。最后對比某典型結構在14、300、500 ℃溫度環境下仿真模擬與實驗測試的結果。在經所提出的算法修正后，結構的有限元模型精度得到了極大的提高。

1 新型改進粒子群算法

1.1 全局粒子群優化算法

全局粒子群優化算法（GPSO）用數學語言可以具體地描述為：在D維空間中，粒子群包含M個粒子。每個粒子表示優化問題的一個備選解，第k迭代步第i個粒子更新公式為

式中：vki=（vi1，vi2，···，viD），為粒子速度向量；xki=（xi1，xi2， ···，xiD），為第i個粒子的坐標位置；pki為粒子歷史最優解；gk為粒子群歷史最優解；°為Hadamard積；c1、c2為加速度因子，一般取值為2；r1、r2為D維的0～1之間的隨機數向量；w為慣性權重因子；K為壓縮因子；w、K一般設置為k的線性或非線性函數

式中：w的變化范圍為［0.4，0.9］，wmax=0.9和wmin=0.4；N為最大迭代總數。

將粒子群信息表示為矩陣形式可寫為

式中：Xk、Vk、Pk（k=0，1，···，N）為M×D的矩陣；M為種群規模。

式（1）的搜索策略的優點是能夠使粒子快速集中至極小值處，但其缺點也很明顯。由于該搜索策略的數據缺乏多樣性，所以算法一旦陷入極小值，則很難跳出局部最優，最終往往難以搜索到全局最優解。

1.2 粒子的萊維飛行搜索策略

假設粒子群中的部分粒子有一定的概率失去先驗的最優位置信息，且此時這些粒子按照萊維飛行進行隨機游走，更新公式為

式中：α為步長控制向量，與xki維度相同，其元素為0～1之間的隨機數；s為步長，服從萊維分布，萊維分布常用Mantegna算法模擬

式中：β為穩定性指數，常取1.5；μ、ν服從正態分布

其中

式中：Γ為標準伽馬函數。

文獻［21-23］分別將萊維飛行融入不同的搜索機制以改進粒子群算法，并在21個基準函數上測試，證明萊維飛行可以對搜索空間進行深度探索，避免了粒子位置多樣性的損失，增強了粒子群算法跳出局部最優的能力。然而對Rosenbrock、Rotated Schwefel等幾類高維、多峰、強非線性函數，單純引入萊維飛行機制仍然很難搜索到理論最優解。

1.3 萊維正交學習粒子群算法

本文提出一種新型的改進粒子群算法，該算法旨在利用萊維飛行的跳躍能力和田口設計的正交學習增強算法的全局搜索能力。首先介紹正交學習過程。

假設為粒子群算法中第i個粒子的3個歷史經驗坐標向量。田口設計以這3個1×D的向量作為水平，且以優化參數的個數D為因子數，則該D因子3水平田口設計正交表可表示為

式中：V為正交表中組合的總數；集合G中-1、0、1代表3個水平。為了清晰直觀地表示出各水平元素的組合，定義函數

應用函數?（x）和矩陣A將矩陣L轉化為3個只有0、1元素的矩陣

式中：A的元素均為1，大小為V×D。經過田口設計后的粒子位置向量組合為

若為最小值優化問題，則令（i=1，2，···，M）中適應度最小的坐標向量為xb。再根據田口設計試驗結果，運用極差分析法找出最優水平組合，其對應的坐標向量定義為xp。最后選擇xb、xp中適應度值最小的向量，記為xkOi。以上過程可以記為

式中：OED代表田口設計及正交學習過程。該過程利用歷史學習經驗構造了一個合理的最佳經驗用于指導粒子的更新。粒子僅使用一個經驗來引導更新，避免了GPSO算法中2種經驗之間的沖突，有利于算法更快地收斂到最優。

在萊維正交學習粒子群算法（LOPSO）中，飛行概率因子f∈（0，1］，當0.5＜f≤1時，將粒子當前位置xki、歷史最優解pki、全局最優解gk作為田口設計的3水平；當f≤ 0.5時，xki按式（4）隨機游走變為萊維飛行項Lxki，此時取Lxki、pki、gki為水平。

當k→+∞時，xki、pki、gk趨于接近，粒子不再更新，算法最終可以收斂。理想狀態下有限元模型與實際模型誤差函數Y最小值應為0，但這幾乎是不可能的。所以設置一個閾值，當適應度值小于閾值時則認為結果收斂。若閾值設置過小時，很長時間的迭代后適應度值仍無法收斂到閾值以內，此時可通過最大迭代步數N來控制算法停止，當迭代步數達到N時亦可停止算法。LOPSO算法的具體步驟如下。

步驟1設置種群規模M、搜索維度D、最大迭代步數N、慣性權重因子最大值wmax和最小值wmin。

步驟2隨機生成初始粒子群信息X0和V0。

步驟3令k=1；根據實驗數據和有限元模型確定目標函數Y=F（X），F-1為其逆函數；評價初始適應度值；并令P0=X0、g0=F-1（minF（X0））。

步驟4根據式（2）計算慣性權重因子ω、壓縮因子K；令i=1。

步驟5歷遍種群中每個粒子，隨機生成飛行概率因子f，根據其大小求XOk

步驟6更新粒子，計算公式為

式中：r為0～1間的隨機數；c為加速度因子，取值2；壓縮因子K、慣性權重因子w的值依照式（2）計算獲得。

步驟7根據式（15）、式（16）更新歷史經驗

步驟8計算所有適應度值，判斷是否收斂或達到最大迭代次數N，若未滿足條件返回步驟4。若滿足條件，則輸出終步的全局最優解，即尋優結果，算法終止。

該算法的特點在于在種群計算時采用一種全新的更新策略，以唯一的最佳經驗作為引導，避免了傳統粒子群算法2種引導經驗之間的沖突，并且飛行概率因子的設計既防止了局部收斂，又保證了算法的有效收斂。LOPSO方法流程如圖1所示。

圖1 LOPSO方法流程圖Fig.1 Flowchart of LOPSO method

2 軸承等效彈簧阻尼參數修正

2.1 仿真算例

通過修正傳動軸系軸承-軸承座等效建模的剛度和阻尼參數，簡單驗證上述算法的優越性。假設傳動軸系通過3對軸承-軸承座與船體固接；軸的一端有一質量盤，軸之間采用聯軸器相接。若僅需修正垂向等效參數，則該模型可在有限元軟件MSC.Patran中簡化為圖2所示的梁單元模型。軸系各處材料相同，密度為7.8×103kg/m3，彈性模量為210 GPa，泊松比取0.3。質量盤和聯軸器簡化為對應位置節點上的附加集中質量。不考慮軸的內阻尼并將軸承-軸承座等效為一端固支的彈簧阻尼單元，則剛度系數k1、k2、k3和黏性阻尼系數c1、c2、c3即為需要修正的參數。

圖2 軸系軸承數值算例Fig.2 Numerical example of shafting bearings

2.2 目標函數

考慮黏性阻尼，多自由度系統頻域運動方程形式為

式中：ω為激振頻率；M、K、C分別為總質量矩陣、總剛度矩陣、總阻尼矩陣；x為位移響應向量；f為激振力向量。對應的頻響函數矩陣為

式中：HD、HV、HA分別為位移、速度和加速度復頻響函數矩陣；為系統在第k自由度上施加單位激勵后第i自由度的加速度響應，可以寫成復數形式

式中：(ω)、(ω)分別為(ω)的實部和虛部。

頻響函數同時包含了剛度和阻尼信息，共振頻域的頻響值主要受阻尼大小的影響，而非共振區的頻響值則與剛度更為相關。因此可以采用單點激振、多點拾振的頻響函數法獲取軸系的動態響應特性。定義實驗測量和計算響應的平均Y向加速度輸出誤差

假設仿真實驗沿y負向加載單點單位激勵，測試頻段為10～2 000 Hz。則fj（ω）=1，可根據式（19）、式（20）定義目標函數Y（k1，k2，k3，c1，c2，c3）

為了模擬真實的實驗狀態并檢驗算法的抗噪聲干擾能力，對仿真實驗測得的加速度頻響添加5%的隨機白噪聲。等效剛度和阻尼的修正問題可以轉化為目標函數Y（k1，k2，k3，c1，c2，c3）的最小值問題，其中k1～k3為剛度系數，c1～c3為阻尼系數。

2.3 修正結果及對比

分別應用PSOLF和LOPSO算法解決上述最小值問題。為了定性地比較分析，控制各算法的總計算次數相等，最大迭代次數N取50，且將2種算法的超參數均設置為：c1=c2=c=2.0，ωmin=0.4，ωmax=0.9。表1展示了優化算法的參數設置及時間成本。圖3中給出了迭代收斂曲線。可以看出當總計算數相同時，PSOLF和LOPSO方法的時間成本大致相同。前20步迭代PSOLF算法搜索得更快，后30步迭代LOPSO算法的優勢逐漸體現。這是由于在迭代前期LOPSO算法中，萊維飛行項Lxki通過正交學習過程與歷史最優解pki、全局最優解gk進行綜合，所以粒子的更新較為謹慎。而PSOLF方法中粒子群得益于萊維飛行項快速向局部優解處聚攏。迭代后期3個引導經驗的相互沖突使得PSOLF算法始終在局部優解附近徘徊。而LOPSO方法最終搜索到目標函數最小值明顯優于前者的搜索結果。這表明LOPSO算法相比于PSOLF算法更不容易陷入局部優解，全局搜索能力更強。

表1 優化算法超參數設置Table 1 Optimization algorithm parameters

圖3 收斂曲線Fig.3 Convergence curves

表2中比較了軸承-軸承座等效剛度和阻尼修正結果。LOPSO方法的修正值更為接近真實值，各參數誤差均小于1%，而PSOLF方法修正后的參數最大誤差超過6%。這進一步說明了本文所提算法搜索精度更高，可以有效應用于工程問題中。

表2 軸承等效參數修正結果對比Table 2 Comparison of updated results of bearing equivalent parameter

3 典型結構熱振有限元模型修正

3.1 典型結構及有限元建模

圖4給出了結構的剖面圖和有限元模型。該結構分為12個部分，頭部后端、二艙、三艙、四艙、尾艙、整流罩、翼面、發動機采用殼單元QUAD4和TRIA3建模；頭部前端、舵面、舵面連接塊、內部支架、內部質量塊、整流罩連接部分以及滑塊采用體單元CTETRA4建模，局部質量差用CONM2進行配平；各艙段連接部位采用加厚殼單元共節點的處理方式進行等效建模。模型材料統一為航空用鋼30CrMnSiA，密度為7 750 kg/m3。

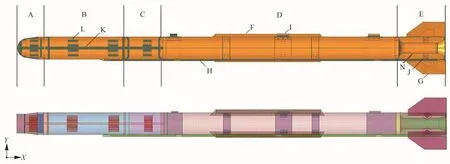
圖4 結構及有限元模型Fig.4 Structure and finite element model

最終有限元模型共計66 272個單元、80 533個節點，其總質量、質心位置和轉動慣量與實際模型的誤差均在3%以內，可忽略不計。如圖5，不同溫度對應的材料熱物性參數不同，因此考慮溫度效的結構動力學計算是一個復雜的非線性過程。

圖5 30CrMnSiA熱物性參數Fig.5 Thermophysical parameters of 30CrMnSiA

3.2 高溫模態實驗

開展地面高溫模態實驗，驗證有限元模型的預示能力。令整流罩中面所在平面為俯仰方向，垂直于該平面方向為偏航方向。

如圖6，結構通過2個彈性尼龍繩吊掛在固定橫梁上，達到近似“自由-自由”的狀態。尼龍繩采用絕熱石棉布包裹進行保護。加熱設備為環抱結構的石英燈陣，在外圍包裹石棉布絕熱保溫，并在激振點和測點處預留小孔。實驗采用單點隨機激勵的方式。激振器水平安裝，并通過耐高溫合金激振桿作用到激振點處。為了遠離高溫區域，力傳感器安裝在激振桿與激振器之間［25-26］。針對俯仰和偏航主模態在長度方向中線位置布置5個激光多普勒測振儀。測量扭轉模態時分別在頭部和尾部兩側各布置1個激光多普勒測振儀。測點和激振點在俯仰和偏航方向上的布置情況分別如圖7、圖8所示。各傳感器通過數據采集器保持同步。考慮對稱性，選取一個舵面進行測試。在舵面一側布置4個激光測振儀，另一側激勵。圖8中編號1、2、3、4的測點在圖示局部系下坐標分別為（25，25）、（141，26）、（253，125）、（19，133）；編號5處是激勵點，坐標為（12，16）。

圖6 高溫模態實驗Fig.6 Modal experiment in high temperature environment

圖7 測量結構俯仰模態時的測點Fig.7 Measurement points when measuring pitch modes

圖8 測量結構偏航模態時的測點Fig.8 Measurement points when measuring yaw modes

實驗測量了14、300、500 °C時的振動數據，其中14 °C為室溫環境。高溫實驗開始前先將實驗件預熱至50 °C，溫升速率為2.5 °C/s，達到預定溫度后保溫60 s。分區加熱器共分為7個控溫區，每個控溫區在結構環向布置4個熱電偶，共計28個溫度測點用于測量和控制溫度，保證整個結構的溫度誤差在足夠的精度范圍內。

模態實驗在0～500 Hz內共獲得8個主要模態，分別為：俯仰一彎、偏航一彎、俯仰二彎、偏航二彎、扭轉一階、舵面彎曲、舵面旋轉、舵面扭轉。采用模態置信準則（MAC）分析有限元計算模態與實驗測試模態的相關性，識別出具有較高MAC值的模態對。圖9給出了與實驗結果匹配的模態振型云圖，其中為了更清晰地顯示振型，扭轉振型圖將翼面及舵面隱藏，舵面振型圖將與其連接的結構主體部分隱藏。有限元模型和實驗測量的模態振型相關度見圖10。所有關鍵模態對的MAC值均高于0.7，說明有限元模型能夠正確地獲得與實驗模態匹配的振型。

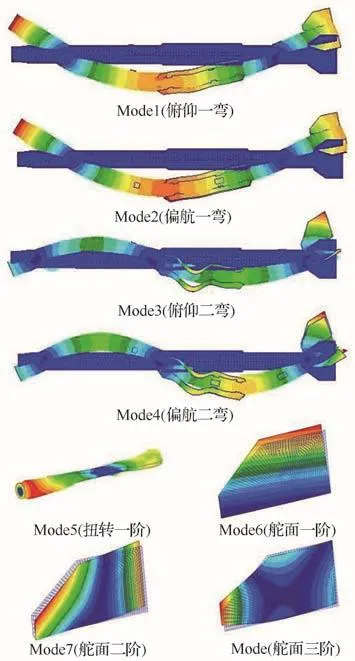
圖9 主要模態振型Fig.9 Main modal shapes

圖10 振型相關系數Fig.10 Correlative coefficient of mode

該結構各艙段、翼面、舵面和整流罩等部件間采用螺栓或螺釘連接，本文在建模過程中對于此類復雜連接結構直接采用共節點的方式進行簡化處理。所以模型總體剛度偏大，初始有限元模型的各階模態頻率都比實驗測量值高。誤差主要來源于此類連接結構處的參數不確定性。

3.3 模型修正

本文建立的有限元模型的質量特性和幾何特性均與實際結構的相應數據進行了核驗。因此，在后續的模型修正問題中，本文假定有限元模型的質量特性和幾何特性數據是可信的，無需進行修正。同時為了降低問題復雜度，本文假定材料的泊松比和熱膨脹系數是可信的，僅修正材料的彈性模量參數。針對14、300、500 ℃這3種溫度狀態下的實驗測量結果，本文暫不考慮高溫下多狀態的修正，分別對各溫度下的彈性模量參數進行修正。彈性模量的不確定性主要表現在結構的連接部位。表3列出了8個主要連接部位的材料的彈性模量參數符號，所有材料的彈性模量初始值均為196 GPa。

表3 不確定的材料參數Table 3 Uncertain material parameters

定義基于結構模態實驗的目標函數

式中：fEMAt、fFEMt分別為測量和計算的模態頻率；t為模態序數；m=8。

直接用有限元模型進行迭代計算需耗費大量的計算力，因此該項研究工作借助開源的Scikit-Learn機器學習框架，構建隨機森林代理模型［27］來近似修正參數和目標函數Y之間的映射關系，提高計算效率。為了降低構造代理模型的復雜度，通過靈敏度分析篩選修正變量。常見的靈敏度計算公式為

式中：xt+=（x1，x2，···，xt+Δxt，···，xn）；xt-=（x1，x2，···，xt-Δxt，···，xn）。該式為有限差分法，通過對變量作微小的攝動Δxt來計算近似導數。

靈敏度計算結果如圖11所示。通過靈敏度計算發現E1W、E2W主要影響舵面模態頻率，靈敏度值最大；由于飛翼的彎曲模態與結構整體的彎曲模態耦合，E1R、E2R也是影響結構彎曲模態頻率值的主要因素。此外E1F的靈敏度也相對較大，所以最終確定有限元模型的修正參數為E1R、E2R、E1W、E2W、E1F，共計5個。

圖11 參數靈敏度分析Fig.11 Parametric sensitivity

表4為結構在14、300、500 ℃下修正前后有限元模型與實驗模型的模態頻率比較，表中ef，b、ef，a分別為修正前、后模態頻率的相對誤差。

表4 實驗與有限元模態對比Table 4 Comparison between measured and FEM modal results for main modes

修正前有限元模型與實驗模型在頻率上差異顯著，室溫14 ℃時頻率誤差最大為35.19%，300 ℃環境下最大誤差為30.63%，高溫500 ℃環境下頻率誤差最大達到37.92%。初始有限元模型的精度和可靠性值得懷疑，通過本文提出的模型修正方法進行修正后誤差大幅降低，14 ℃時8階頻率的最大誤差僅為4.63%，300 ℃情況下最大誤差僅為6.79%，500 ℃時的最大誤差僅為5.16%，動力學有限元模型精度得到提高。修正后的參數變量如表5所示。各連接部位單元的彈性模量修正值均小于初始值。這是由于連接處的等效建模導致結構的剛度過大，僅選擇彈性模量作為修正參數，剛度的減小僅靠彈性模量的減小來實現，修正結果相當于局部結構的等效彈性模量。

表5 單元彈性模量修正情況Table 5 Comparison of parameters before and after modal updating

4 結論

1） 為求解復雜環境下結構動力學有限元模型修正等非線性優化問題，提出了萊維正交學習粒子群算法。該算法基于田口設計和正交學習選擇最優的組合解作為唯一的更新引導，避免了傳統算法中2種經驗之間的沖突；同時引入萊維飛行機制增強算法跳出局部最優的能力。該新型改進粒子群算法不僅避免陷入局部最優，而且可以快速收斂獲得更精確的解。

2） 軸承-軸承座等效彈簧阻尼參數修正結果表明，相比于其他先進的粒子群算法，所提出的算法搜索到的最優解最為接近真實值，精度更高。本文方法在仿真噪聲的干擾的情況下，修正后剛度誤差僅為0.5%，阻尼誤差僅為0.3%，可以有效應用于復雜的結構動力學工程問題中。

3） 將LOPSO方法成功應用于高速飛行器熱環境下的有限元模型修正。采用本文修正算法的動力學模型具有較大的預測精度，為理解工程結構在熱振耦合條件下的動力學特性提供了一種可靠的方法。