面向任務需求的模塊化無人機配置方法

肖和業，楊建峰，白俊強，*，張旭東，吳利榮

1.西北工業大學 無人系統技術研究院，西安 710072

2.中國人民解放軍 95889部隊，酒泉 735018

3.中國人民解放軍 96236部隊，北京 100085

無人機集群具有數量規模大、體系彈性抗打擊、運用場景豐富、任務用途可配置等特點，是左右未來戰場勝負的關鍵手段［1-2］。而無人機集群在多種運用場景下多樣化的任務用途需求，增加了無人機大規模制造的復雜度，使其無法有效地控制成本，制約了無人機大規模集群運用［3］。因此，面向多任務用途需求及成本約束下，如何實現無人機大規模的集群運用，就成為了一項亟需研究的課題。

無人機屬于工業產品之中的一類，其面向多任務用途的大規模制造及運用問題從本質上來看，是如何實現產品大規模定制化設計、制造及配置的問題。關于這一問題的研究在近十年來備受關注［4-6］，許多學者在解決該問題上也提出了很多有效的方法及理論［7-10］。例如，李浩等［8］提出了面向大規模個性化的產品服務系模塊化設計框架，通過物理與服務的內部模塊組合，實現客戶需求的大規模、個性化、低成本及快速配置。張英英等［9］提出一種主從關聯優化方法，以解決產品族配置與升級的再制造設計問題。杜綱等［10］建立了模塊化設計產品平臺配置協同優化的主從關聯優化雙層規劃模型。該模型能夠比較準確地描述現實生產中模塊化產品設計與平臺配置之間的關聯關系，實現了在產品設計生產中的成本控制。雖然以上研究中采用的方法、理論有所不同，但依然可以發現其共性特點，即通過模塊化產品設計和配置實現產品大規模定制化制造及運用的成本控制。依此類推，通過模塊化產品設計及配置方法能夠解決無人機集群多種任務用途需求與大規模運用成本相互制約問題。

模塊化產品設計方法已在無人機中得到運用，且各種概念模塊化無人機層出不窮［11-13］，并提出了一系列的設計理論及方法。而模塊化無人機配置方法作為無人機大規模個性化制造及運用中的關鍵環節，尚無成熟的理論及研究。因此，為了構建模塊化無人機設計［14-16］到產品配置的閉環理論方法體系，需要開展模塊化無人機配置方法研究，進而為無人機大規模制造及集群運用提供有效的理論基礎。

產品配置方法已有很多學者開展了相關研究，從原有實現單一產品性能方案與客戶需求匹配［17-18］、發展到解決多個產品族與客戶多樣化需求相匹配的問題［9-11］。不僅如此，為了提升產品配置的經濟性、時效性，配置方法中還將產品的利潤效益、成本、周期等因素作為約束引入到優化配置中，并通過加權算法［19］、粒子群算法［17，20］、遺傳算法［9-10，20］來實現產品配置及方案優化。

基于以上研究基礎，本文面向集群無人機多用途的作戰需求，在模塊化無人機配置方法中創建從用途到需求的映射層，以構建用途、需求、性能到備選元素屬性的多層映射網絡；針對無人機集群在激烈對抗中易發生損耗、使用次數有限的特點，在配置方法中將成本作為約束條件，結合各模塊備選元素成本調研數據，開展配置方案優化，以實現成本控制；基于無人機多種類部件復雜的關聯關系，在多層、復雜映射網絡中，采用改進粒子群方法在成本約束下搜尋由用途、需求、性能到元素屬性的最優映射路徑，獲得配置最優的方案，實現模塊化無人機配置對不同用途下多樣化需求的精確響應。以文獻公開算例為例，采用本文優化算法、遺傳算法進行方案配置并對其結果進行對比，驗證本文算法的正確性。由此，提出一種模塊化無人機配置方法，與模塊化無人機設計方法相匹配，以解決無人機大規模集群運用中多種任務用途需求與成本無法有效匹配的難題。

1 模塊化無人機配置核心思想

模塊化設計是實現產品大規模定制化模式的有效手段，核心思想是通過構建通用模塊與專用模塊的快速組合，實現客戶多樣化需求的大規模、定制化、低成本與快速提供。為了適應多樣化任務用途并便于大規模制造，無人機基于此思想已開展了模塊化設計的研究［11-12］，各種類型的模塊化無人機也孕育而生。在現有模塊化無人機系統中的模塊，可以分為通用模塊和專用模塊2大類。通用模塊是指模塊度總體較高的，與其他模塊聯系緊密，基本上不需要進行選擇，且不受使用方需求影響的模塊，該類模塊具備系統反復使用的基礎功能。專用模塊是指某一方面或幾方面關聯度較高，需要根據需求進行適當選擇，可以實現系統某一方面或幾方面功能的模塊，該類模塊使得系統能夠根據需求，衍生出多樣化的能力，是對通用模塊的拓展。

基于模塊化無人機模塊劃分方法［21］，無人機能夠將零件歸并、聚合形成多個可組合的模塊，并辨識出通用模塊和專用模塊。而如何對通用模塊與專用模塊進行匹配、組合以滿足多樣化任務需求，就成為了一項有待研究的課題，也是模塊化無人機從設計到面向任務能力生成的關鍵環節。為此，本文在模塊化設計基礎上進行無人機模塊配置研究，以通用模塊為無人機能力構成的基礎，通過挑選和配置能夠滿足任務需求的專用模塊，從而配置出滿足多樣化任務需求的無人機，如圖1所示。

圖1 模塊化無人機配置策略示意圖Fig.1 Basic idea of modular UAV configuration

2 方法介紹

2.1 總體架構及流程

與其他機電類產品不同，無人機包含電子、機械、動力、毀傷等多種功能部件，且組成復雜、零件數量多。在多種任務用途的要求下，無人機總體性能與部件屬性的關聯關系更為繁雜、多樣，這使得無人機的配置變為復雜的非線性尋優過程，提升了無人機配置問題的難度。不僅如此，集群無人機在大規模應用時，成本是整個應用的關鍵影響因數，需要在成本約束下開展無人機的配置研究。因此，在無人機部件與性能復雜映射關系下，最大程度滿足任務性能需求并實現對無人機成本的控制，就成為了無人機配置優化的難點。

針對無人機配置的難點，本文將基于“通用模塊+專用模塊”的配置思想，構建適合模塊化無人機的模塊配置方法。首先，對任務需求和模塊備選元素進行描述，建立需求集和模塊備選元素集，以無人機性能為“橋梁”，構建任務需求與模塊備選元素之間的關聯關系。然后，以專用模塊備選元素的成本為約束條件，建立需求滿意度評價模型，采用粒子群算法進行迭代計算，最終獲得最優的無人機專用模塊配置方案，模塊配置流程見圖2。

圖2 模塊化無人機配置流程圖Fig.2 Flow chart of modular UAV configuration

2.2 任務需求及專用模塊備選元素表征

2.2.1 任務需求的模型化表征

需求是客戶對產品外形特征、功能等諸多方面的期望標準，根據以往研究結果，需求類別大致分為描述型、解釋型、參數型、二元型、選項型等，由于任務需求問題具有一定的模糊性，同時又要進行一定的量化分析。因此，本文采用半結構化的描述性需求類型，通過建立需求集對無人機的任務需求進行描述。設無人機需求集為

式中：Dr表示第r類需求；R為需求的種類數量，無人機任務需求為其中一類需求，每一類需求中又包含多個具體的需求，即

其中：p為第r類需求的數量，dri為需求因子，表示第r類需求中的第i個需求，無人機的需求集描述見圖3。因此，需求集D可表示為

圖3 任務需求描述示意圖Fig.3 Schematic diagram of task requirements description

2.2.2 專用模塊備選元素表征

針對無人機總體性能指標需求，在氣動布局、總質量確定的情況下，通過總體性能設計模型［22］，可以獲得各部件的性能要求。基于無人機模塊劃分方法［21］，對各部件進行模塊劃分及聚類，明確模塊與部件的隸屬關系，結合現有貨架產品的情況，可以獲得滿足性能要求的部件備選元素集。由于不同的模塊包含不同的零部件，且零部件也有不同的備選元素，通過對備選元素的描述，使得零部件的特點更加清晰，進而明確模塊的特征屬性，達到表征模塊屬性的目的。本節對專用模塊備選元素進行描述，設專用模塊備選元素集為

式中：c為模塊數；Mi表示第i個模塊，其可表示為

其中：mik為第i個模塊中的第k個零部件，每個零部件又具備多個備選元素，即

其中：z為備選元素數量；bikq表示第i個模塊中的第k個功能部件的第q個備選元素。

模塊的構成屬性可以用模塊內功能部件的備選元素集進行表征，即為模塊構成屬性的數學形式，具體見圖4。以第i個模塊為例，其第k個零部件中包含zk個備選元素，用備選元素集進行描述可表示為

圖4 專用模塊備選元素與模塊構成屬性映射關系示意圖Fig.4 Mapping relationship between dedicated module alternative elements and module composition attributes

2.3 模塊配置模型構建

2.3.1 關聯關系評判標準

構造關聯性矩陣之前，首先需要明確關聯關系的評判標準，基于面向客戶需求配置方法的研究成果，本文將關聯度分為4個等級［20，23-24］，具體情況見表1。

表1 關聯關系評判標準Table 1 Evaluation criteria of correlation relationship

2.3.2 關聯性矩陣的構建規則

1）性能與需求綜合關聯性矩陣

設無人機任務類需求集為

式中：P為任務類需求的總數，各個需求對應的權重定義為

設無人機包含L個性能，其性能集可表示為

式中：Hl表示無人機的第l項性能，各項性能對應的權重定義為

則無人機性能-需求關聯性矩陣可表示為

式中：alm表示第l個無人機性能與第m個需求之間的關聯度，考慮需求的權重后，得到無人機性能-需求綜合關聯行矩陣，可以表示為

式中：λlP為表示第l個無人機性能與全部P個任務需求的綜合關聯度，其表達式為

2）備選元素與性能綜合關聯性矩陣

設專用模塊的備選元素集為

專用模塊備選元素-性能關聯性矩陣可表示為

式中：表示第i個模塊與無人機性能之間的關聯性子矩陣，第i個模塊內包含備選元素的數量為Ni，則M(i)M-H可表示為

綜合考慮無人機性能權重后，構造專用模塊備選元素-性能綜合關聯性矩陣，其可表示為

式中：δij，l表示第i個模塊的第j個備選元素與L個無人機性能的綜合關聯度，其表達式為

其中：i=1，2，…，n；j=1，2，…，Ni。

3）備選元素與需求關聯性矩陣

以無人機性能為“橋梁”，建立專用模塊備選元素和任務需求之間的關聯關系，即根據矩陣M*H-D和M*M-H可以得到備選元素-需求綜合關聯性矩陣，其可表示為

式中：ξij表示第i個模塊中的第j個備選元素與多用途任務需求集的關聯度，表示該備選元素對全部需求的滿足程度，其表達式為

4）權重系數獲取方法

為確保客觀反映各指標間的權重關系，本文引入了專家評分機制，通過邀請無人機設計領域專家，確保結果的準確性。

為此，制定了《無人機模塊配置相關權重評議表》，邀請m個專家進行n組權重預估。

式中：rq為第q個專家的權重預估組

其中：rqn為第q個專家對第n項權重系數的評估值。

為降低專家評分的主觀因素影響，采用基于專家信度［21］的方法，考慮評分專家的職稱、從事專業和從業年限等要素，設置信度評分標準（見表2），確定每個影響因素的權重，綜合得到m個專家的評分質量信度值ui(i=1，2，…，m)。

表2 專家評分質量標準Table 2 Quality standards for expert evaluation

然后，計算專家信度系數：

式中：U=[u1，u2，…，um]，fi值越大表示專家的權威性越大，其所占權重越大。因此，專家的評價權重可表示為

則q個專家的權重集為

結合專家權重，得到最終的指標權重集為

2.3.3 需求滿意度評價模型構建

1）備選元素選擇向量

采用二進制數表示專用模塊備選元素是否被選中，即“1”表示該備選元素被選中參與無人機專用模塊配置，“0”表示未被選中。據此建立專用模塊備選元素選擇向量

式中：εij=1表示專用模塊備選元素mij被選中參與模塊配置，εij=0表示未被選中；v表示專用模塊備選元素總數。

2）需求滿意度評價模型

根據無人機專用模塊備選元素-需求關聯性矩陣以及選擇向量，構造需求滿意度評價模型Y=εM*M-D，具體表達式為

采用模塊成本作為模型的約束條件，設專用模塊的成本向量為

式中：zij表示第i個模塊的第j個備選元素的成本，則第t種配置方案對應的成本可表示為

2.4 基于粒子群算法的優化模型求解

面向無人機多種性能需求進行模塊化無人機的配置，根本上是一個組合優化問題，同時要滿足規定成本的要求，此時優化配置問題可描述為

式中：S為模塊化無人機的產品性能與任務需求的適應度，是需求滿意度的倒數即1/Y， 其值越小，代表性能與任務需求越貼合；N為功能模塊數量；Ni為第i個模塊內備選元素數量；εik為模塊內元素配置決策量；ξik為備選元素與無人機性能需求的相關度；Zt為無人機配置方案成本；Zp為無人機可承受成本的上限。

由于無人機功能多、組成復雜，其性能關聯矩陣較其他產品更為復雜，形成了多層的關系網絡，從此復雜的關系網絡中搜尋出最優的配置路徑，需要采用高效的優化搜尋方法。不僅如此，由于無人機運用還有成本控制的要求，應在優化配置中還要確保方案滿足成本的約束。而粒子群算法搜索速度快、效率高，適合于約束滿足問題的特點［17，25-26］，使得粒子群算法較其他優化方法能夠更好地求解本文復雜映射網絡下最優關系搜尋的問題。同時，模塊化無人機劃分方法［21］中也采用了粒子群算法進行模塊劃分方案的尋優，為了與模塊化無人機模塊劃分方法保持一致，形成模塊化設計到配置的閉環體系，模塊化無人機配置方法中優化方法選用粒子群算法更為合適。綜上所述，本文配置模型采用粒子群方法來實現方案的優化配置。

由于模塊化無人機配置是從各模塊備選元素進行優化組合的過程，每個模塊中每個部件的備選元素不能為空。因此，粒子群初始向量設定時，按每個模塊各部件備選元素不能為空的約束進行隨機生成；在迭代更新過程中，粒子每個模塊各部件備選元素不能為空，如為空則需要對空的模塊進行備用元素適應性填充。同時，為了實現在無人機性能與需求復雜關聯關系中的高效搜尋，在標準粒子群算法中引入了時變加速因子和時變權重系數［25］，以提高粒子群搜索前期的速度和范圍，具體公式為

式中：時變加速因子c1、c2變為

其中：c1max、c1min、c2max、c2min分別為加速因子的最大值和最小值；ti為實時迭代次數；T為最大迭代次數。

同時對變慣性權重w進行調整，具體為

式中：ωHmax、ωHmin分別為慣性權重的最大值和最小值，T、ti與式（37）中相同。采用改進后的粒子群算法能夠避免陷入局部最優解，并且當收斂到最優解時，對解進行微調，達到提高全局最優解精度的目的，整個優化配置的具體步驟如下：

步驟1初始化參數。隨機生成多個選擇向量ε(i)，i=1，2，…，Nq，Nq為粒子群數量，以此作為粒子群的初始位置，代入式 （29）、式（32）計算粒子群適應度模型，從向量ε中通過排序得到局部最優和全局最優的初始值對應的位置pij(t)和gij(t)，并通過式（30）和式（31）計算相應的成本Zt。

步驟2通過式（34）和式（35）更新向量ε，代入式 （29）、式（32）計算粒子群對需求的適應度，通過排序得到局部最優和全局最優的初始值對應的位置pij(t)和gij(t)，計算相應的成本Zt。

步驟3如果成本滿足約束條件，進一步通過式（34）、式（35）更新向量ε，重復步驟2；如果成本不滿足約束條件，重置向量ε，重復步驟2。

步驟4通過以上迭代、形成最優配置方案。獲得滿意度全局最大的粒子位置向量ε。

整個算法的偽代碼如偽代碼1所示。

在向量ε挑選出選擇向量中“1”對應的備選元素，即為專用模塊的配置方案，結合通用模塊配置方案，得到模塊化無人機配置方案。

偽代碼 1 粒子群算法偽代碼輸入：MM-H； %類模塊與產品性能相關度矩陣；MH-D； %客戶需求與產品性能的相關度矩陣；WH； %MM-H權值矩陣；WD；%MH-D權值矩陣；Z；%各功能類模塊價格向量輸出：最佳選擇gbest和最佳適應度S；1.C=MM-H·WH+MH-D·WD； %綜合權值；2.粒子群初始化；3.For 迭代次數4.For 粒子個數5.新適應度與個體歷史最佳適應度做比較；6.個體歷史最佳與種群歷史最佳適應度做比較；7.End 8.If 模塊內未選擇任何元素9.隨機選擇；10.End 11.記錄最小適應度S及對應的最佳選擇gbest；12.End

2.5 算法驗證

為了驗證本文算法，以文獻［20］的綜合適應度矩陣為輸入，以適應度為目標函數，價格約束設為Zt＜130萬元，采用本文算法對文獻［20］的產品進行方案配置，粒子群算法中取粒子數N=20，迭代次數T=50，加速因子c1max=c2max=2.5，c1min=c2min=0.5，慣性權重ωHmax=0.9，ωHmin=0.4。同時基于遺傳算法［27］，在基因編碼、交叉和變異環節根據無人機模塊備選元素的選擇特點調整每段基因的編碼及變化策略，在交叉環節設置隨機數量的交叉點位對遺傳算法進行改進。進而采用此遺傳算法對例子進行了分析，整個種群大小設置為20，交叉概率設置為0.3，變異概率設置為0.1。遺傳算法、改進粒子群算法經過數次迭代，種群適應度收斂如圖5所示。通過優化得到目標函數適應度的最小值為0.027 2，即最大滿意度為36.81。需求滿意度最大的配置方案為：空心車軸、彈性車輪、三相異步電機、轉臂式一系懸掛，該結果與文獻［20］中的優化配置方案一致。

圖5 最小適應度隨迭代次數變化曲線Fig.5 Variation of maximum fitness with number of iterations

為了全面考核本文算法的有效性，采用種群內最小適應度以及整個種群的平均適應值隨迭代次數的變化作為參考，對本文算法、遺傳算法、文獻中的遺傳算法進行比較，如圖5和圖6所示。同時，將上面3種算法的適應度、迭代次數與局部收斂次數進行比較，結果見表3。盡管遺傳算法效果也明顯優于原文獻中的遺傳算法，且平均適應度在前幾步收斂還略快于改進粒子群算法，但改進粒子群算法的最大適應度收斂速度明顯優于其他2種算法。另外，考慮到2種算法在群體規模，初始化等方面的差異，以算法初次達到最優解時適應度函數的計算次數為衡量指標，可以更精準地比較算法的實際計算效率，其結果見表3最后一列。改進粒子群算法的適應度函數實際調用次數為235，遺傳算法的調用次數為810。從算法結構看，遺傳算法每次迭代對適應度函數的調用次數為初始種群數量的3倍，而改進粒子群算法的模型調用過程僅為完整更新一次粒子的當前適應度，因而節省了計算資源。因此，通過以上計算結果的分析、對比，不僅驗證了本文提出配置方法的正確性，還表明本文提出配置方法具有收斂速度快的優勢。

表3 3種優化方法結果比較Table 3 Comparison of results of three optimization methods

圖6 平均適應度隨迭代次數變化曲線Fig.6 Variation of average fitness with number of iterations

3 無人機配置實例

本節針對單兵無人機應用的典型任務場景，以文獻［21］中的一次性使用無人機作為研究對象，采用其模塊劃分結果作為輸入，開展模塊化無人機配置的實例研究。

3.1 任務場景描述

我方與某國爆發局部沖突的背景下，我方特種部隊前出敵方實際控制區域進行滲透作戰，行至某河谷地區發現敵情，經過偵查發現敵方規模為連級單位，活動范圍約為4 km2，配備步槍，重機槍、單兵防空火箭彈等武器，構筑有臨時營地，其附近配備有若干防空火力和崗哨，可能存在隱蔽的火力點。經過綜合判斷，其可能為敵方前沿指揮所，通過研究制定了無人機、地面人員空地協同作戰任務。集群無人機前出進行偵察，獲取敵詳細分布及火力配置，并作為誘餌誘使敵方暴露隱蔽火力點，通過多波次的偵察與攻擊，清除有威脅的火力點，為地面部隊開辟安全通道，實現地面部隊對其指揮所進行殲滅。其中，無人機的任務主要分為以下2個階段。

階段1單兵便攜式無人機執行情報搜集任務。基于偵察任務需求，對攜帶的無人機模塊進行適應性配置，構建具備偵察能力的無人機，隱蔽接近任務區域進行地形偵察，搜集人員數量、分布位置、火力配置等信息，并向后方進行實時回傳態勢。同時，對可疑區域進行循環偵察，并進行試探性攻擊，誘使敵方暴露隱蔽火力點，由周圍無人機完成隱蔽火力點偵察，完成任務后進行回收，其間無人機被擊落后，由地面人員根據偵察任務進展情況視情進行補充。

階段2單兵便攜式無人機執行定點清除任務。基于搜集的任務區域詳細情報，生成精準攻擊任務需求，配置戰斗模塊、發射與回收模塊的發射方式，組成具備精確制導和攻擊能力的無人機，根據已搜集的情報對任務區域多個具有威脅的火力點同時進行定點清除。任務場景示意見圖7。

圖7 任務場景示意圖Fig.7 View of UAV task scenario

3.2 無人機配置模型構建

3.2.1 任務需求獲取

依據任務場景中對無人機的使用需求，建立需求集，具體見表4。

表4 無人機任務需求Table 4 Mission requirements of UAV

根據表4可得到一次性使用無人機的需求集：

3.2.2 無人機性能分析

根據任務需求，對一次性使用無人機的性能要求進行分析，建立性能集，具體情況見表5。

表5 無人機性能要求Table 5 Performance requirements of UAV

則一次性使用無人機的性能集可表示為

3.2.3 專用模塊備選元素表征

基于文獻［21］中的一次性使用無人機的模塊劃分結果，通過“通用模塊+專用模塊”的策略對模塊進行配置。由于結構模塊具備集成度高、輕量化、成本低等特點，將其劃為通用模塊之一；飛控模塊的控制原理及工程運用方式較為成熟，且在組成上大同小異，可以作為通用模塊之一。其余模塊可作為專用模塊參與配置。

基于市場調研、詢價、預估，給出了備選元素對應的成本，具體情況見表6。

表6 一次性使用無人機專用模塊備選元素Table 6 Alternative elements of special-use modules for disposable UAVs

3.2.4 無人機需求與備選元素關聯性分析

任務場景中階段1、階段2的任務需求存在差異，階段1任務的主要目的是搜集情報，對任務區域的人員分布、火力配置、地形環境等情況進行偵察，對無人機的偵察能力要求較高；階段2任務則是定點清除任務，對有威脅的火力點進行攻擊，要求無人機具備攻擊能力。為了完成以上任務，可采用偵察型與攻擊型無人機構成的異構無人機集群，也可以采用察/打一體的同構無人機集群，為了研究本文算法對2種集群運用下的無人機配置效果，構建其任務能力需求圖，如圖8所示。

圖8 不同階段任務需求差異Fig.8 Differences in task requirements at different stages

1）建立無人機性能-需求關聯性矩陣

依據一次性使用無人機的性能與任務需求的關聯關系，得到一次性使用無人機性能-需求關聯性矩陣為

邀請10名無人機設計領域專家進行評分。經計算，然后取兩位有效數字，分別確定任務需求的權重wD和無人機性能的權重wH為

2）無人機專用模塊備選元素-性能關聯性矩陣

根據一次性使用無人機的專用模塊備選元素與無人機性能的內在關聯，針對2個階段的任務需求，結合無人機性能模型［22］，分析得到專用模塊備選元素與無人機性能之間的關聯關系。

3）偵察型無人機備選元素與性能關聯矩陣

根據階段1任務需求，需要配置出具備偵察能力較強且可以回收的無人機。因此，該型無人機沒有戰斗模塊，偵察型無人機專用模塊備選元素-性能關聯性矩陣為

式中：

偵察型無人機專用模塊備選元素的成本矩陣為

4） 攻擊型無人機備選元素與性能關聯矩陣

基于階段1獲得的情報，階段2的攻擊型無人機主要執行攻擊任務，搭配經濟型的制導設備和戰斗模塊，對有威脅的火力點進行定點清除，因此，該型無人機無需回收，其專用模塊備選元素-性能關聯性矩陣為

攻擊型無人機專用模塊備選元素的成本矩陣為

5）察/打一體型無人機備選元素與性能關聯矩陣

采用察/打一體型無人機執行階段1的偵察任務同時完成階段2的打擊任務，需要配置性能合適的偵察模塊以及戰斗模塊，整個無人機無需回收。因此，其專用模塊備選元素-性能關聯性矩陣、成本元素矩陣，與攻擊型無人機的專用模塊備選元素-性能關聯性矩陣、成本元素矩陣相同。

3.3 配置結果及討論

3.3.1 約束條件設定

本文將無人機的成本作為配置的約束條件，設定實現此次任務的無人機的成本為10萬元左右，其中，需要配置的專用模塊約為7萬元。因此，將模塊配置的成本約束設置為7萬元，具體情況見表7。

表7 無人機成本情況Table 7 Costs of parts of UAV

3.3.2 不同需求下無人機配置結果

1）偵察型無人機配置結果

采用粒子群算法對滿意度模型進行仿真計算。首先，進行初始值設置，粒子群規模N=30，最大迭代次數T=100，加速因子c1max=c2max=2.5，c1min=c2min=0.5，慣性權重ωHmax=0.9，ωHmin=0.4，進行方案尋優。為了驗證本文算法，同時采用遺傳算法進行了方案配置，遺傳算法交叉概率設置為0.55，變異概率設置為0.1，2種算法種群適應度隨迭代次數的收斂曲線如圖9所示，此時適應度為0.002 52，遺傳算法與粒子群算法得到配置方案結果相同。從圖9可知遺傳算法的迭代次數45次要多于粒子群算法29次，由此驗證了本文提出配置方法的正確性及其收斂速度快的優勢。

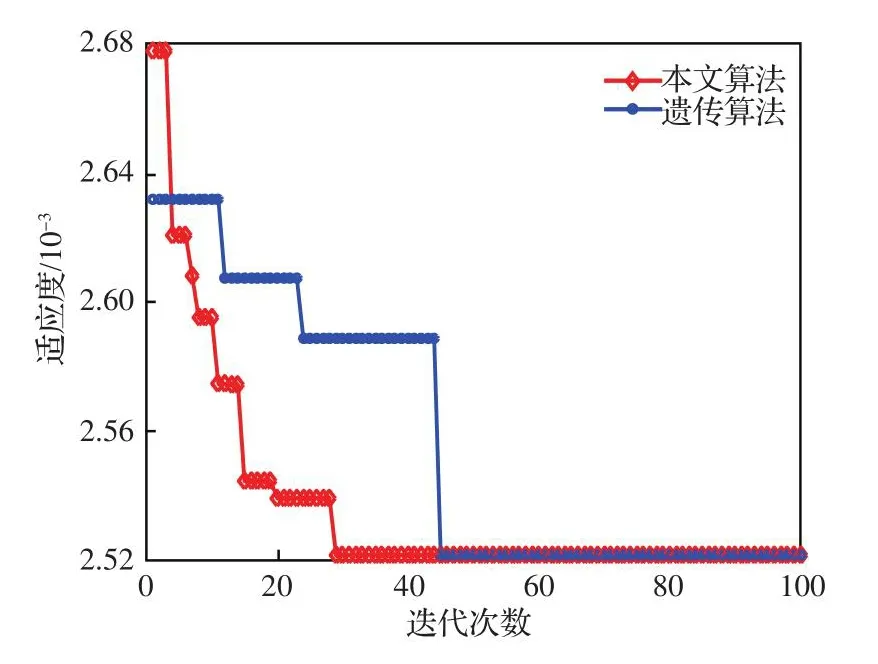
圖9 偵察型無人機優化收斂曲線Fig.9 Optimal convergence curves of surveillance UAV

最優滿意度值對應的選擇向量為

通過最優選擇向量挑選出對應的專用模塊備選元素，組成偵察型無人機的專用模塊配置方案，其成本總和為65 740元，滿足成本約束條件，具體情況見表8。

表8 偵察型無人機專用模塊配置方案Table 8 Configuration plan of special-use modules for surveillance UAV

2）攻擊型無人機配置結果

粒子群初始參數設置與偵察型無人機一致，在25步左右，配置優化過程達到最優解，最優滿意度值對應的選擇向量為

依據選擇向量挑選出對應的備選元素，組成攻擊型無人機的配置方案。其中，動力模塊選擇LY X3120電機、HY電子調速器、鋁合金槳夾、碳纖維槳葉；通信與電源模塊選擇6S鋰電池、集成式電源管理板、3 km數據鏈、數據鏈共型天線、單光導引頭；控制執行模塊選擇碳纖維平尾、垂尾、GDW DS1906B舵機；發射與回收模塊為燃氣組件；戰斗模塊選擇電子引信、0.5 kg戰斗部，結合表6可以計算的到配置方案對應的成本為47 540元，滿足約束條件。

3）察/打一體型無人機配置結果

粒子群初始參數設置與偵察型無人機一致，在30步左右，配置優化達到最優解， 最優滿意度值對應的選擇向量為

依據選擇向量挑選出對應的備選元素，可得察/打一體型無人機的配置方案。其中，動力模塊選擇LY X3120電機、HY電子調速器、鋁合金槳夾、碳纖維槳葉；通信與電源模塊選擇6S鋰電池、集成式電源管理板、5 km數據鏈、數據鏈柱狀天線、雙光導引頭；控制執行模塊選擇碳纖維平尾、垂尾、GDW DS1906B舵機；發射模塊為燃氣組件；戰斗模塊選擇機械引信、0.5 kg戰斗部，結合表6可計算得到無人機對應的成本為69 790元，滿足約束條件。

3.3.3 配置結果分析及對比討論

依據案例任務中偵察、攻擊、察/打一體3種需求，本文算法在成本約束下對各模塊中的備選元素進行了選取，實現了3種任務需求下模塊化無人機模塊的高效配置。由于模塊化無人機尚無采用成熟配置方法進行模塊配置的相關案例，本文通過模塊化無人機的配置方案與公開文獻［28-29］中現有單兵用無人機的參數配置進行對比驗證。通過對比可知：偵察型無人機的參數配置與美國“龍眼”無人機的性能、配置相近；攻擊型無人機的參數配置與美國“彈簧刀”性能、配置接近；察/打一體型無人機性能與以色列“hero-30”無人機性能、配置相近，而以上無人機已在案例所述場景中得到了成功的運用。通過以上對比表明：模塊化無人機配置方案能夠實現對不同任務需求的匹配。不僅如此，模塊化無人機的成本還能夠滿足成本約束。由此可知，本文提出的模塊化無人機配置方法能夠實現無人機性能、成本與多種任務用途需求的協同匹配。同時，也驗證了本文提出算法的合理性。

從無人機模塊配置過程中可以發現模塊化無人機各模塊的元素性能與成本直接相關。因此，模塊化無人機配置方案就直接決定了其成本價格。為了進一步揭示本文的模塊化無人機配置方法對其單機成本、集群應用成本的影響，本文將從模塊化無人機單體成本占比、面向任務運用成本2個層次開展討論分析。

1）成本占比分析

面向不同任務需求形成的模塊化無人機配置方案中，結構模塊成本為5 000元，飛控模塊成本為25 000元，動力模塊4個部件價格為305元、265元、50元、120元，通信與電源模塊中鋰電池、電源管理模塊、數據鏈、共形天線、導引頭價格分別為5 000元、1 500元、20 000元、900元、25 000元，控制執行模塊價格為1 400元，發射與回收模塊為1 200元。飛控模塊、通信與電源模塊在整機成本中占比較高，其中飛控、數據鏈、導引頭這3個部件成本之和占單機成本的70%以上。尤其在偵察型無人機中，由于偵察任務對圖像獲取及數據傳輸能力的需求更高，數據鏈、導引頭部件成本占整機成本的比例達50%以上，具體如圖10所示。雖然察/打一體無人機通過本文算法在要求價格范圍內獲得滿足需求的配置方案，但偵察、攻擊需求解耦配置后，偵察型無人機能夠通過配置重復回收模塊實現多次使用以控制成本，打擊型一次性使用無人機可以選配滿足要求的低端部件以控制成本。由此可知，通過需求的動態調整，結合模塊化無人機配置方法，能夠實現對模塊化無人機單機成本的控制。

圖10 偵察型無人機成本占比圖Fig.10 Cost proportion of surveillance UAV

2）無人機任務運用成本

對于案例中的運用場景，可以通過察/打一體無人機一次性完成2個階段的任務，也可通過偵察型無人機完成第1階段任務，攻擊型無人機完成第2階段任務并回收偵察型無人機，這2種無人機的任務運用模式會帶來成本上的差異。基于現有的模塊化配置方案，針對區域內不同攻擊目標個數，可以獲得模塊化無人機任務運用的成本曲線，如圖11所示。在攻擊目標個數＜2個時，采用察/打一體無人機成本比偵察型與攻擊型組合的無人機成本低。當攻擊目標個數＞2個時，采用偵察型與攻擊型組合的無人機成本比察/打一體無人機成本低，并且隨著目標個數增加即無人機使用數量的增加，偵察型與攻擊型組合的無人機成本優勢越為明顯。因此，基于模塊化無人機配置方法，不僅能在成本約束下構建無人機配置方案，還能結合無人機任務運用模式對成本進行調控，進而為無人機大規模集群運用提供成本控制的途徑。

圖11 目標數量與任務成本曲線Fig.11 Task cost varied with target number

4 結論

面向無人機任務需求，本文基于“通用模塊+專用模塊”的模塊化無人機設計思想。以無人機性能為“橋梁”，建立了任務需求和模塊備選元素之間的關聯關系，構造了需求滿意度評價模型，并結合改進粒子群優化方法實現了無人機配置方案的高效獲取。針對已有案例，采用本文算法及遺傳算法開展配置優化分析，得到了相同的優化方案結果，驗證了本文優化算法的有效性，進而提出了一種面向任務需求的模塊化無人機配置方法。以具體任務場景的無人機使用需求為牽引，結合模塊化無人機模塊劃分方法研究成果，采用本文提出的模塊配置方法在預定成本約束下構建了偵察、攻擊、察/打一體等3型無人機的模塊配置方案，并與文獻中單兵無人機的參數配置對比，驗證了配置方案的合理性。各配置方案成本的計算結果表明：本文提出的模塊化無人機配置方法能夠實現無人機性能、成本與多種任務用途需求的協同匹配，進而解決了無人機多種任務需求與其性能、成本無法精準匹配的難題。不僅如此，通過不同任務需求下模塊化無人機配置方案單體成本占比、面向任務運用成本的對比分析可知：本文提出的模塊化無人機配置方法與任務需求相結合使用，能對無人機單機及集群運用成本具有一定的控制作用。