基于視圖互信息加權的多視圖集成聚類算法

勞景歡，黃 棟*，王昌棟，賴劍煌

（1.華南農業大學 數學與信息學院，廣州 510642；2.中山大學 計算機學院，廣州 510006）

0 引言

聚類分析（clustering analysis）是一類重要的無監督學習技術，其目標在于將一組給定數據點劃分為若干小類，每一個小類稱為一個簇（cluster），以期簇內數據點盡可能相似，不同簇的數據點盡可能不同［1］。傳統聚類算法大多關注單視圖數據，即數據集僅有一個數據源（或僅有一個特征集）；而在現實應用場景中，數據來源往往多樣化，同一個數據集也可能有多個數據源的特征集，由此構成多視圖數據（multi-view data）。傳統聚類算法［2-4］的單視圖學習模式往往難以有效應對多視圖聚類問題，如何充分利用多視圖場景下不同數據視圖之間的互補與一致信息提升多視圖聚類性能，是近年來聚類分析領域的一個熱點研究方向［5-17］。

近幾年，國內外研究人員提出了許多行之有效的多視圖聚類算法［5-12］。Tang 等［12］提出了一種基于跨視圖相似圖融合的多視圖聚類算法，通過跨視圖擴散，學習得到一個統一的圖相似性矩陣，并在該統一相似性矩陣上進行譜聚類，生成聚類結果。Khan 等［11］提出了一種基于流形優化的多視圖聚類算法，通過構造一個聯合的拉普拉斯矩陣，以包含所有單視圖去噪處理后的簇信息，再使用k均值（k-means）聚類和Stiefel 流形方法優化聯合聚類目標，減少聯合視圖和單個視圖之間的聚類信息分歧。Zhang 等［18］提出了一種新的單步共識多視圖子空間聚類算法，構建統一學習框架以同時學習得到相似性矩陣、共識表示和最終聚類標簽矩陣。

這些多視圖聚類算法在聚類性能上取得了較大改進［11-12，18］，但這些算法往往無差別對待所有視圖，未充分考慮視圖間的重要性差異，對于低質量視圖也給予同等對待，可能導致低可靠度信息或噪聲信息在計算過程中持續傳播，對最終聚類結果產生負面影響，因此，多視圖加權機制近年來越來越得到重視，許多具有視圖加權能力的多視圖聚類算法［19-23］也相繼提出。Wang 等［20］提出了一種基于圖的多視圖聚類算法，通過多視圖權值、單視圖相似性和統一相似性三者之間的相互迭代更新，得到優化后的權值和統一圖矩陣，再對統一圖矩陣進行秩約束并得到最終的簇劃分。Chen等［21］提出了一種基于多視圖加權融合和離散化矩陣分解的多視圖譜聚類算法，通過對不同視圖加權學習得到統一相似性矩陣，對相似性矩陣進行特征分解得到一組特征向量，進而從特征向量中學習一個連續的聚類標簽，將其離散化以建立最終聚類。Huang 等［22］提出了一種同時執行核空間多視圖聚類任務和學習相似性關系的多視圖聚類模型，可在構建準確的相似圖、自動分配最優權重的同時得到最終聚類指示矩陣。這些算法對多視圖聚類的加權機制進行了多角度的探索，但這些算法大多依賴于特定目標函數的迭代優化，且往往涉及一個或多個超參數的預設或精調，其目標函數的適用性及超參數設置的合理性均對實際應用有較大影響。如何自動、高效地得到多視圖可靠度及其權值，構建魯棒聚類結果，仍是目前多視圖聚類研究的一個挑戰性問題。

針對前述問題，本文提出一種基于視圖互信息加權的多視圖集成聚類（Multi-view Ensemble Clustering based on View-wise Mutual Information Weighting，MEC-VMIW）算法。該算法可分為視圖互加權階段和多視圖集成聚類階段兩個階段。在視圖互加權階段，首先對數據集進行多次隨機降采樣，在單次降采樣的數據集中對每個視圖構建一個聚類結果，利用多視圖的降采樣聚類集合評價每個視圖內的聚類結果，再取它們的平均得分，得到各個視圖的一個評價分數；然后，將此降采樣、構建降采樣聚類、視圖評價過程重復T次，可得各視圖的T個評價分數，以它的最終平均得分作為視圖權值。在多視圖集成聚類階段，借助集成聚類的思想［24-30］，在各個視圖中構建多個基聚類（base clusterings），再將多個基聚類結果建模至二部圖（bipartite graph）模型，進而作高效二部圖分割以得到最終聚類結果。

1 本文算法

1.1 視圖互信息加權機制

本文提出視圖互信息加權機制，在無監督情況下可用來評價多視圖數據中不同視圖的可靠度并對它賦予相應權值。為降低運算規模，同時提升多次運行時的多樣性，首先對原始數據集進行隨機降采樣，采樣比例γ∈(0，1]；在具體實現中，令γ=0.5，即每次降采樣時保留一半數據點。進一步地，在降采樣所得的數據點中，計算它們的歐氏距離，并以高斯核函數將它們映射至相似度，再取它們的K近鄰（K-Nearest Neighbors，KNN），構建一個稀疏的K近鄰相似性矩陣，其中，高斯核函數的帶寬參數（bandwidth parameter）設置為K近鄰圖距離的平均值。在得到相似性矩陣的基礎上，通過譜聚類（Spectral Clustering，SC）算法［2］分別得到每個視圖的一個聚類結果。

然后，借助歸一化互信息（Normalized Mutual Information，NMI）［31］對每個視圖的聚類結果與其他視圖的聚類結果進行相互評分。對于任意的兩個基聚類πi和πj，計算公式如下：

通過多個視圖的降采樣聚類結果以NMI 進行相互評分，可以對不同視圖之間的聚類結果一致性或認可度進行評價，并將獲得其他視圖認可（得分）更高的聚類（及其對應視圖）視作具有更高可靠度，由此確認視圖間權重。針對單次視圖互評可能存在的偶然性，本文將前述過程重復T次，得到平均互評得分。

在單次視圖互評的基礎上重復運行T次，可得每個視圖的平均評價分數，將它作為視圖權重。令Wv表示為第v個視圖的T次互評平均得分（即權重），計算如下：

由此，通過視圖互信息加權機制，可以得到各個視圖間的權重W={W1，W2，…，WV}，其 中Wv表示第v個視圖 的權重。

1.2 視圖基聚類生成策略

集成聚類的目標在于融合多個基聚類結果的信息以得到一個更優、更魯棒聚類結果［27］。常規集成聚類往往以k均值聚類算法生成基聚類集合，雖然k均值聚類算法具有計算簡單、效率高等優點，但聚類結果對質心選取的依賴程度高且難以有效應對非線性可分數據集。譜聚類與k均值聚類算法相比，可生成任意簇形狀的聚類結果，有效應對非線性可分數據集，因此本文采用譜聚類算法生成多視圖基聚類。

為了得到更優聚類結果，本文將對多視圖數據的多個基聚類進行集成，構造簇與數據點之間的二部圖結構，然后以高效圖分割算法得到最終的聚類結果。該二部圖中，包含數據集的所有樣本點。若使用降采樣的方式得到具有部分樣本的基聚類，將不能構造具有正確權值的二部圖。為此，與視圖互加權階段使用降采樣數據集不同，基聚類生成過程使用的是完整數據集。為充分挖掘各視圖信息，本文為每個視圖生成M個基聚類，由此為多視圖數據集得到總計M×V個基聚類。在每個視圖中，本文基于歐氏距離與高斯核函數映射構造數據點的相似性矩陣，進而構建其K近鄰相似性圖，然后利用譜聚類算法對其進行劃分。對于所有的基聚類，如果它們的簇數均相同，可能得到的基聚類集合較為單調。對于每一個基聚類，如果簇數偏離真實的簇數過大，則可能得到準確性較差的基聚類。為了使所構建的基聚類集合具有多樣性，對每個基聚類的簇個數在隨機選取，其中y表示該數據集的真實類別個數。對于V個視圖，在每個視圖中生成M個基聚類，將第v個視圖所生成的基聚類集合記作：

其中視圖v的第i個基聚類表示為，令nv，i表示簇個數，則有：

值得注意的是，在1.1 節中基于視圖互信息加權機制已經得到各個視圖的權重W={W1，W2，…，WV}，進一步將之與各個視圖的基聚類集合相結合，即得到基聚類權重，即在視圖v的基聚類集合Πv內的基聚類對應獲得視圖v的權重Wv。

1.3 二部圖建模與多視圖集成聚類

在構建多視圖基聚類集合Π的基礎上，將對多個基聚類的信息進行融合，構建最終的多視圖聚類結果。本文采用二部圖結構對多基聚類的集成過程進行建模。在基聚類集合中，每個基聚類包含若干個簇，將全體基聚類所包含的簇集合表示為：

其中NC表示簇的總數。顯然，全體基聚類的簇個數等于各個基聚類簇個數之和，即NC=

具體地，以簇集C和數據點集X為節點集，將集成聚類問題構造為加權二部圖模型。所建立的加權二部圖結構如圖1 所示。當兩個節點同為簇節點或者同為數據點節點時，兩節點之間沒有邊的連接；當且僅當一個節點為數據點節點、另一個節點為簇節點且該簇中包含了這個數據點時，兩個節點之間才有邊的連接，兩者之間連接邊的權值由該簇隸屬的基聚類權值所決定。

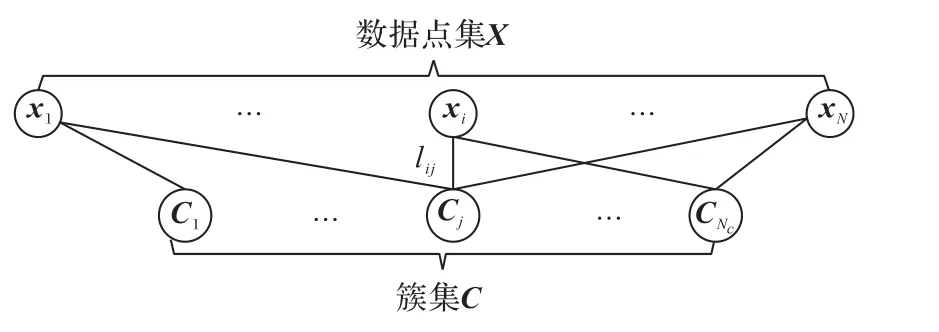
圖1 加權二部圖G示意圖Fig.1 Schematic diagram of bipartite graph G

該二部圖結構表示如下：

其中：X和C表示二部圖G的兩部分節點集合，L為圖G的邊集合。對于任意的兩個節點xi和Cj，邊的權值定義如下：

其中：xi是數據點節點，Cj是簇節點。xi隸屬于Cj且xi所在的基聚類隸屬于視圖v的基聚類集合Πv，則xi與Cj之間的權值由視圖v的權值所決定。基于二部圖的結構特點，可使用遷移分割（transfer cut）算法［32］將該二部圖結構高效劃分為若干互不相交的節點子集，將每一個節點子集中的數據點視作一個簇，得到最終的多視圖集成聚類結果。

2 實驗與結果分析

本章在6 個多視圖數據集上進行實驗，并將本文提出的基于視圖互信息加權的多視圖集成聚類（MEC-VMIW）算法與譜聚類算法及4 個多視圖聚類算法對比分析。

2.1 數據集與對比算法

本節實驗將在6 個多視圖數據集上展開，分別是3Sources、Notting-Hill、Reuters、Mfeat、Caltech-7、Caltech-20，具體信息如表1 所示。

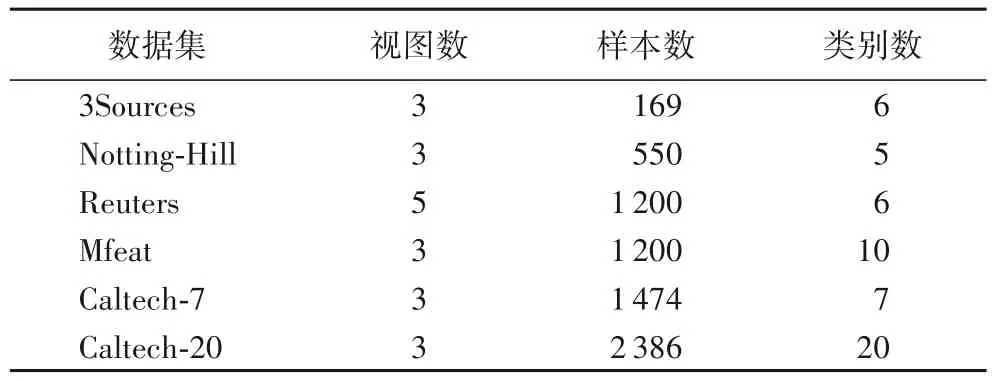
表1 實驗數據集Tab.1 Experimental datasets

將MEC-VMIW 算法與5 個單視圖和多視圖聚類算法進行對比，對比算法分別是：SC 算法［2］、RMSC（Robust Multi-view Spectral Clustering）［33］、AWP（multi-view clustering via Adaptively Weighted Procrustes）［9］、MCGC（Multi-view Consensus Graph Clustering）［34］和CoMSC（Multiview Subspace Clustering via Co-training robust data representation）［17］。

在這些對比算法中，SC 算法是單視圖聚類算法，SC-Avg表示SC 算法在所有視圖取到的平均得分，SC-Best 表示SC 算法在所有視圖中取到的最高得分；RMSC、AWP、MCGC 和CoMSC 是多視圖聚類算法。

2.2 參數設置與評價指標

為了實驗的公平性，在所有對比實驗中，首先將數據集進行歸一化處理。在各個數據集的實驗中，每個算法均重復運行20 次，取其平均得分及標準差作為評價標準。

在MEC-VMIW 算法中，構建K近鄰相似性矩陣所采用的近鄰個數設置為K=10，視圖互加權過程中降采樣次數設置為T=10，基聚類生成過程中每個視圖的基聚類個數設置為M=10。值得一提的是，本文算法對不同參數設置具有很好的魯棒性，可在所有數據集中使用相同參數配置。在各個對比算法中，本文采用對應論文中的參數設置。

在評價指標上，本文采用歸一化互信息（NMI）［31］和調整后蘭德指數（Adjusted Rand Index，ARI）［27］這兩個常用指標評價聚類性能，其中：NMI 的取值范圍為［0，1］，ARI 的取值范圍為［-1，1］，NMI 與ARI 的得分越高，表示所得聚類結果與真實類標越契合，即聚類性能越好。

2.3 與其他算法的對比實驗

本節將在6 個多視圖數據集上對MEC-VMIW 算法與5個對比聚類算法進行對比分析。各個聚類算法在數據集上的NMI 與ARI 分數分別如表2、3 所示。

表2 本文算法與其他聚類算法的NMI得分 單位：%Tab.2 NMI scores of the proposed algorithm and other clustering algorithms unit：%

如表2 所示，本文算法在4 個數據集上取得了最高NMI得分，并且MEC-VMIW 算法的平均NMI 得分為60.80%，顯著高于其他對比算法。除本文算法之外，AWP 算法取得了第二高分的平均NMI 得分，僅為54.16%。

如表3 所示，本文算法在ARI 得分方面也表現出類似優勢，平均ARI 得分為53.61%，顯著高于取得次高的平均ARI得分45.20%。AWP 算法雖然在Caltech-7 和Caltech-20 等兩個數據集上ARI 得分小幅高于本文算法，但它在3Sources、Notting-Hill、Reuters 等數據集上的ARI 得分均顯著低于本文算法，特別是在Reuters 數據集上AWP 算法的ARI 得分僅為2.42%。相較于其他對比算法，本文所提出的多視圖集成聚類算法也表現出更為魯棒的聚類性能。

表3 本文算法與其他聚類算法的ARI得分 單位：%Tab.3 ARI scores of the proposed algorithm and other clustering algorithms unit：%

2.4 參數分析

本節將在6 個多視圖數據集中對MEC-VMIW 算法的參數K、M的敏感性進行分析，驗證MEC-VMIW 算法在不同參數配置下的聚類魯棒性。

在構建K近鄰相似性矩陣過程中，參數K表示近鄰個數。為驗證近鄰個數K對MEC-VMIW 算法的聚類性能影響，本文令K的取值在｛5，10，15，20｝變化，得到在不同的K值下MEC-VMIW 算法的NMI 與ARI 得分，如圖2、3 所示。由實驗結果可以看到，MEC-VMIW 算法在不同的近鄰數K下表現出相當穩定的聚類性能，在同一個數據集中，得到的結果的NMI 和ARI 的表現的波動趨勢較為一致。MEC-VMIW 算法在3Sources、Mfeat 和Caltech-20 等數據集中，隨著K的增大，得到的NMI 值呈單調遞增/遞降趨勢，但均在K=10 之后逐漸收 斂。在Notting-Hill、Reuters 和Caltech-7 等數據集中，K∈[10，15]時得到的分數最高。由于在K=10、15、20 的得分較為穩定，不妨將K設置在［10，20］區間，可對不同數據均為較好的魯棒性。在本文實驗中，對所有數據集均采用K=10的統一設置（從結果來看，取K=10 和取K=15 的性能差不多，甚至K=10 更好；結合運算時間成本，由于K越大需要的計算時間越多，所以選擇K=10 更為合理）。

圖2 不同K值下MEC-VMIW算法的NMI得分Fig.2 NMI scores of MEC-VMIW algorithm at different K values

圖3 近鄰個數K的不同取值下MEC-VMIW算法的ARI得分Fig.3 ARI scores of MEC-VMIW algorithm at different K values

在基聚類生成過程中，M表示每個視圖基聚類個數。為驗證單個視圖基聚類個數M對MEC-VMIW 算法的聚類性能影響，本文也令M的取值在｛5，10，15，20｝變化，得到在不同的M值下MEC-VMIW算法的NMI與ARI得分，如圖4、5所示。

圖4 每個視圖基聚類個數M的不同取值下MEC-VMIW算法的NMI得分Fig.4 NMI scores of MEC-VMIW algorithm at different M values

圖5 每個視圖基聚類個數M的不同取值下MEC-VMIW算法的ARI得分Fig.5 ARI scores of MEC-VMIW algorithm at different M values

需要注意的是，在具有V個視圖的多視圖數據中，單視圖基聚類個數為M則意味著多個視圖的總基聚類個數為M×V。如圖4、5所示，本文算法在不同M取值下表現出較穩定的聚類性能，其中M∈[10，15]是它在不同數據集下的建議取值。在本文實驗中，本文對所有數據集均采用M=10的統一設置。

3 結語

本文提出了一種基于視圖互信息加權的多視圖集成聚類（MEC-VMIW）算法，主要過程可分為視圖互信息加權和多視圖集成聚類這兩個主要階段。在視圖互信息加權階段，所提算法首先對數據集進行多次隨機降采樣，在每次降采樣數據集中構建各視圖聚類結果，并以其聚類結果互評價策略得到各視圖評分，進而將此降采樣、構建降采樣聚類、視圖評價過程重復若干次以得到最終平均得分，并將之作為視圖權值。在多視圖集成聚類階段，本文借助于集成聚類的思想，在各個視圖中構建基聚類集合，進而將其建模至二部圖結構，再以高效二部圖分割算法得到最終多視圖聚類結果。在多個數據集上的實驗結果驗證了本文所提出多視圖集成聚類算法的有效性與魯棒性。在未來研究工作中，可繼續探索本文方法在缺乏多視圖數據、大規模多視圖數據上的進一步擴展。