低頻振動環境下壓電能量轉換裝置響應特性

梁夢凡,李福松,金功偉

(西安機電信息技術研究所,陜西 西安 710065)

0 引言

傳統意義上,微機電系統(MEMS)和無線傳感網絡(WSN)節點供電主要依賴于化學電源[1]。化學電源可穩定、高效地對電能進行直接存儲或釋放。然而,在特殊工作環境下,化學電源存在體積大、工作周期有限和需定期人為更換等缺點。考慮到MEMS和WSN器件低能耗的特點,微能量收集裝置應運而生[2]。相比于傳統的電池供電,能量收集器具有特殊環境匹配性高、長壽命和小體積等優點,被廣泛應用于健康檢測[3]、傳感[4]、醫療器械[5]和環境檢測[6]等領域。能量收集器利用電磁效應、靜電效應或壓電效應等將外部激勵(風能、機械能和電磁能等)轉化為電能輸出,常見的有摩擦納米發電機(TENG)[7],電磁發電機(EMG)[8]和壓電納米發電機(PENG)[9]等。振動能是生活中常見的機械能量之一,可由飛機機翼、發動機引擎和運輸裝作業等過程產生,因此,研究振動能量收集器對解決特殊環境下低功耗器件能源保障問題具有重要意義。其中,壓電式能量收集器(PEH)由于結構簡單、抗電磁干擾和小尺寸等優點逐漸成為研究熱點之一[10-12]。

雖然前人對PEH裝置做了大量研究工作,提出了許多具有新穎結構的壓電收集器,但多數研究局限于單因素優化策略。壓電發電的功率密度較高,發展趨于MEMS化,對于懸臂梁結構的PEH器件轉換電路多為標準整流電路,因此該結構設計過程存在的不足有：1) 收集器體積較大,一階振動頻率較高,難以應用于低頻環境;2) 收集器振動結構使壓電材料的工作模式單一,不能有效收集多振動模式下的能量等。因此,針對典型應用場景如周圍震動環境實時檢測、觸摸設備能量回收和智能穿戴自供能等,外界環境的振動隨機性和非線性對能量收集器的材料參數、外接負載大小、結構剛度和裝置尺寸提出更加苛刻的設計要求,只有不斷優化壓電能量收集裝置的結構才能最大程度提高其輸出性能和可靠性。針對低頻振動環境下微功耗電子器件結構與性能關系不明確問題,通過有限元方法探究壓電微能量收集裝置多參數對其輸出響應特性的影響,為設計新型能量收集裝置和電能源轉換技術提供一定的指導作用。

1 PEH工作原理

1.1 壓電方程

傳統PEH裝置原理主要運用以壓電材料作為核心結構的壓電方程,在一定邊界條件下,通過電位移矢量(D)、應力張量(T)、電場強度(E)和應變張量(S)四種物理量將力-電關系以數學形式表現出來。其中,邊界條件可分為電學和機械兩類,根據約束條件的不同,方程類型和適用場合也不同。機械約束條件分為自由和夾持兩種,對應的方程在電學中分別為開路和短路,在特定條件下,機械-電學方程可以實現相互轉換,兩種機械條件和兩種電學條件情況結合而組成四種不同情況,分別對應①～④類。只有在滿足對應的約束條件下壓電方程才成立,同時也只反映在對應約束條件下所對應的各物理量關系,具體參數如表1所示。

表1 壓電方程參數對應情況Tab.1 Parameter description of piezoelectric equation

此外,壓電材料在工作過程中通過振動產生的縱向、橫向應力作用于壓電片上從而有效輸出電能,該工作模式下壓電材料受外力,壓電片邊界被束縛不能發生自由形變,符合機械夾持條件,而再無電場力作用但電位移矢量不為零時,電勢能由機械能轉換而來,此時滿足電學短路的約束條件,因此本文選擇第②類條件。

對于PZT壓電材料而言,d31耦合模式下產生的形變大于d33耦合模式,因此PEH采用d31機電轉換模式,旨在通過最低的成本,最大程度地提升該裝置的綜合輸出性能。

1.2 機電耦合模型

圖1(a)所示為PEH裝置結構示意圖,由支撐材料、壓電材料、振動質量塊和固定支座組成,通過系統振動可帶動壓電材料沿y方向往復運動,壓電材料的極化強度矢量P平行于y軸。圖1(b)所示為懸臂梁壓電振子等效結構圖,兩層壓電材料負極與負極相連,正極與正極相連,壓電層的極化方向相反。該結構體系下,質量塊M受自身重力作用,同時存在機械結構剛度系數Ks、阻尼系數Cs和壓電材料引起的外界激勵Fp。因此,系統的機械方程可表示為

(1)

圖1 壓電能量轉換裝置模型Fig.1 Piezoelectric energy harvester model

文獻[13]研究表明,PEH裝置可等效為電流源與負載并聯,因此,根據基爾霍夫定律可知

(2)

聯合式(1)和式(2)可得到負載為等效電阻時系統的機電耦合方程,求解該方程組即可得壓電能量收集器機械參數與輸出性能關系,并探究體系結構(質量組成、壓電材料比重和結構剛度等)對壓電發電機響應特性的影響。

2 PEH響應特性

2.1 PEH有限元仿真

壓電材料作為PEH裝置最核心部件,其性能直接影響系統的輸出電性能,常見的壓電材料性能參數見表2[14]。

從表2數據可知,鋯鈦酸鉛(PZT)材料具有較大的壓電系數和較高的機電耦合系數,作為一種較理想的壓電材料,被廣泛應用于壓電裝置,因此本文選擇PZT為壓電材料。為了在有限元模型中得到良好的受力效果,本文的支撐材料和質量塊均選擇結構鋼[15]。通過Comsol 5.2軟件構建的圖1(a)結構有限元模型參數見表3。

表2 常見壓電材料參數[14]Tab.2 Parameter description of piezoelectric materials

表3 有限元模型參數Tab.3 Parameter description of finite element model

圖2 壓電能量轉換器有限元模型Fig.2 Finite element model of PEH

為了簡化計算,本文采用頻域響應求解器分析二維結構模型,利用表3參數進行建模得到的初始結構(對照模型)PEH裝置幾何形狀如圖2所示。設置初始負載R為10 kΩ,正弦激勵加速度為1g,面外尺寸設置為14 mm[16],支撐材料和壓電材料阻尼類型簡化為各向同性,損耗因子均設置為0.001,通過定義接地端口和終端實現圖1(b)所示的等效電路,頻域參數化掃描范圍設置為71～91 Hz,模擬步長為1 Hz,容差最大迭代次數設置為25,容差因子和殘差因子分別設置為1和1 000。

圖3為PEH裝置響應特性。由圖3(a)和3(b)可知,該裝置的有效響應頻帶為75～88 Hz,且隨著外界激勵頻率的增加,PEH裝置的輸出電壓和功率均呈現出先增加后減少的趨勢。當外界激勵頻率為81 Hz時,PEH的輸出電壓和負載功率均達到最大值,分別為3.58 V和 0.64 mW,此時激勵頻率與系統固有頻率一致。在系統固有頻率附近,輸出電壓和功率都呈現出類似對稱的變化過程。為了分析PEH最佳工作狀態時的響應特性,圖3(c)為81 Hz時PEH輸出電壓和功率隨負載電阻的變化。仿真結果表明,隨著負載電阻從102～105Ω變化時,輸出電壓呈現出先迅速增加后緩慢趨于3.86 V穩定電壓的增長趨勢;同時,PEH的輸出功率隨外接負載先增大,達到最大值(R= 3 162 Ω,P= 0.96 mW)后減小。PEH輸出功率可表示為

(3)

式(3)中,ω為諧振頻率,a為加速度。

圖3 PEH響應特性Fig.3 Response characteristics of PEH

根據式(3)可知,當外接負載與內阻電路相等時,即R=π/(2Cpω)=3 162 Ω,此時PEH達到最佳工作狀態。因此,在設計PEH裝置時,需根據內部等效電阻情況添加合適的負載電路,若所配負載過小,兩端電壓和功率都很小,若負載電阻遠大于等效電阻,電路中電流過小會導致裝置功率低。圖3(d)為輸出電壓和功率隨加速度激勵的變化情況,由圖可知,加速度由0.25g增加到4g時,對應的輸出電壓(功率)分別由0.89 V(0.04 mW)增加到14.3 V(10.26 mW)。值得注意的是,在諧振頻率下(81 Hz),輸出電壓隨加速度呈線性相關,而功率與加速度呈二次函數關系。

圖4為PEH裝置在不同頻率下工作的效果圖,可以看出在共振頻率處端口處壓電材料表面的電勢最大,因此可在負載兩端產生最大的輸出電壓,與上述分析結果一致。

圖4 PEH裝置工作效果圖Fig.4 A working renderings of PEH

2.2 PEH特性分析

2.2.1傳感質量塊對PEH響應特性的影響

保持其他輸出參數與建模條件不變的情況下,通過改變傳感質量塊的大小(質量),分析重量對PEH輸出響應特性的影響,模擬結果如圖5所示。圖5(a)為在外接電阻為10 kΩ,加速度大小為1g時,不同尺寸末端質量塊的頻率響應關系,隨著質量塊邊長(a∶b)由1∶1增加到1∶4時,有效響應頻帶由118～142 Hz降低為40～52 Hz,PEH體系的固有頻率逐漸降低,輸出電壓逐漸增大從開始的131 Hz(1.88 V)過渡到最終的46 Hz (10.07 V),同時曲線形狀也更為陡立。因此,通過改變外部質量塊的重量,不僅可以降低PEH固有頻率和能量轉換效率,還可以調整裝置對振動頻率的敏感特性。在PEH系統中,外接負載阻抗匹配可有效增加能量輸出,圖5(b)為電壓和功率(內插圖)隨外部負載響應關系,不難看出,不同質量比時,輸出電壓隨電阻的變化相一致,呈現出先迅速增加后變緩慢并趨于平衡的趨勢,當負載電阻為10 kΩ時,不同質量比對應于不同的穩定電壓,質量比為1∶4時產生的電壓(11.32 V)比1∶1時(2.44 V)提高了3.6倍。同時,隨著負載電阻由102Ω增加到105Ω,不同質量比下,每個PEH存在對應最佳負載值,并在此達到輸出功率最優。圖5(c)為不同質量比下加速度響應規律,由圖可知,輸出電壓和輸出功率與加速度(合外力)分別呈現出線性和二次函數關系,隨著外部激勵的增加,輸出電壓和功率均增加,該曲線也能從側面反映電壓和輸出功率關系。

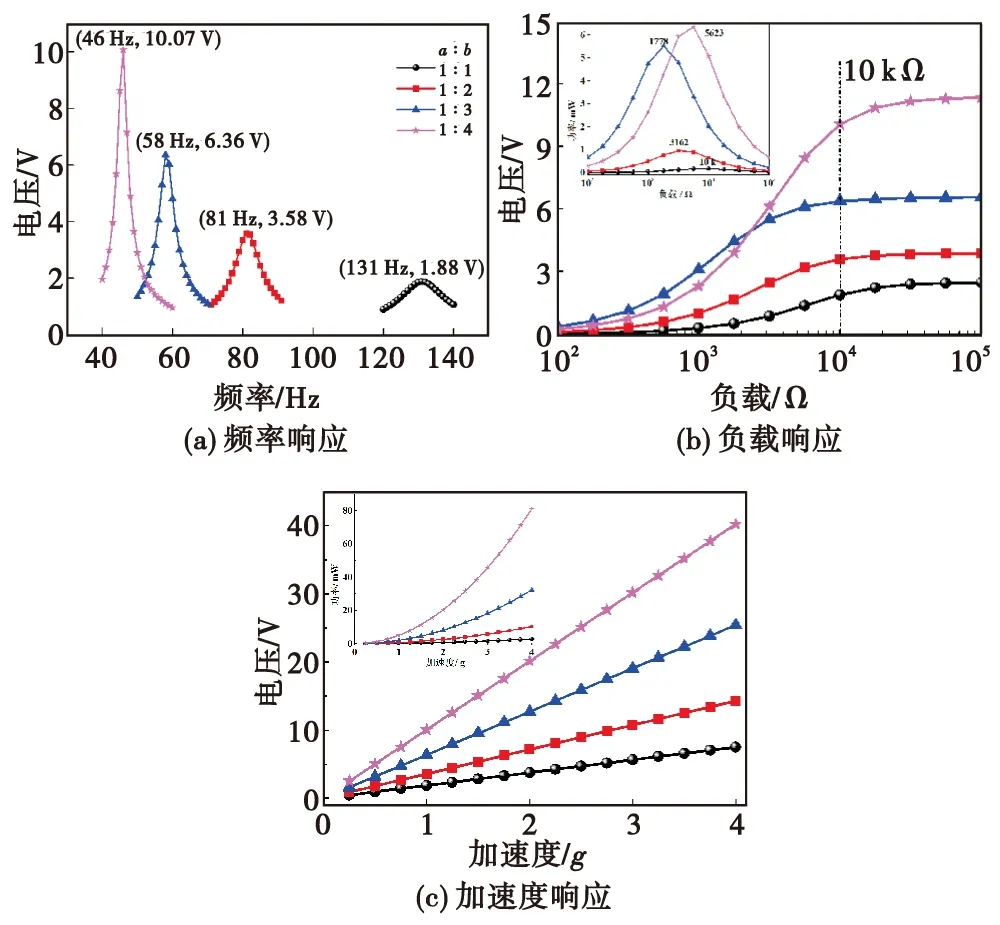
圖5 質量分布對PEH的影響Fig.5 Effect of mass distribution on PEH

2.2.2質心分布對PEH響應特性的影響

為了探究傳感質量塊質心分布對PEH響應特性的影響,在保證傳感質量塊體積不變的情況,改變其形狀(質量塊長寬比分別設置為1∶4、2∶2和4∶1),分析質心分布對PEH裝置響應特性的影響。圖6(a)所示為輸入加速度激勵為1g,外接電阻為10 kΩ時,可看出質量塊長寬比從1∶4增加到4∶1時,整個體系的固有頻率逐漸降低,從87 Hz下降到78 Hz,降低了10.34%,此時,輸出電壓不斷增高,從3.50 V增高到3.62 V,增高了3.43 %。圖6(b)所示為輸出電壓和輸出功率隨外接負載的變化,可以看出不同質心分布下,輸出功率隨負載變化曲線具有相同的變化趨勢,長寬比從1∶4與2∶2時具有相同的系統等效負載,即5 623 Ω時體系輸出性能最優;當長寬比為4∶1時,輸出功率在3 162 Ω時達到最大0.92 mW。觀察輸出電壓變化曲線可知,除了陡變區域(103～104Ω)有細微差別外,保證相同體時,不同質心分布對電壓的影響并不明顯,此規律也可體現在圖6(c)中。當外界激勵從0.25g增加到4g時,三種形狀的傳感質量塊的輸出電性能對加速度響應規律相同。由上可知,當系統質量恒定而改變其質心分布時,可以使整個系統的共振頻率發生改變,同時質心分布對體系輸出電壓不敏感,因此在特定工作情況下,可在保證整體質量不變而改變傳感質量塊形狀以滿足應用要求。

圖6 質心分布對PEH的影響Fig.6 Effect of distribution of the center of mass on PEH

2.2.3壓電材料厚度對PEH響應特性的影響

PEH裝置的能量最優化設計中,除了關注系統本身結構的設計外,還需要注重核心壓電部件對整體性能的影響,當選定所需壓電材料后,其薄膜厚度會明顯影響PEH輸出電性能。圖7所示為不同厚度壓電材料對PEH裝置輸出響應特性的影響。由圖7(a)可知,當電壓厚度由0.03 mm增加到0.09 mm時,輸出電壓的振幅逐漸較小,其變化趨勢與輸出功率相似,是系統的剛度增大所致,導致壓電單元的應變降低。PEH諧振頻率由41.06 Hz右移至125.44 Hz,同時,負載電壓峰值由4.62 V降至3.26 V,輸出功率峰值由1.09 mW降至0.47 mW。由圖7(b)可知,隨著壓電材料厚度增加,PEH裝置的最大輸出功率呈現減小趨勢,由1.35 mW降低至0.52 mW,同時,阻抗匹配度也隨之變化,負載的改變可導致能量耗散程度變化。圖7(c)所示為PEH在不同厚度時的加速度相關性,與上述分析結果一致,輸出電壓和輸出功率隨外加激勵分別呈現線性和二次函數關系,且隨著厚度增加,體系加速度響應的敏感性逐漸降低。因此,在保證壓電材料承重強度下,適當地選擇較薄壓電層,可在低頻諧振頻率下獲得更高的峰值電壓和更好的傳感靈敏度。

圖7 壓電材料厚度對PEH的影響Fig.7 Effect of thickness of piezoelectric material on PEH

2.2.4壓電材料分布對PEH響應特性的影響

不同工況會對懸臂梁式PEH的力學強度提出不同的要求,壓電材料作為壓電發電機最核心部件,分析其在振動臂上的分布對裝置輸出響應尤為重要。本文在確保支撐材料厚度一定,且支撐材料長度與壓電材料長度比為1∶1時,探究壓電材料的分布位置對PEH裝置的影響。根據圖8(a)可知,壓電材料由靠近固定端(左側)到振動收集端(右側)時,體系的諧振頻率由83 Hz右移至124 Hz。值得注意的是,壓電材料在右側時體系的峰值電壓(5.78 V)明顯高于其在左側(5.00 V)和中間(3.86 V)。由圖4可知,靠近振動能量收集側的懸臂梁形變最嚴重,因此,可推測當壓電材料趨于右側分布時會使體系的能量轉化效率明顯提升。由圖8(b)可知,隨著壓電材料向振動收集側分布,最大功率由0.96 mV增加到2.23 mV,增加了133%。此外,壓電材料的分布并不改變體系的阻抗匹配,且隨著負載由102～105Ω變化時,在3 162 Ω前,輸出電壓隨外界負載的變化趨勢基本相同,且變化大小無明顯差別,當負載超過體系等效電阻時,靠近振動能量收集端的體系輸出電壓隨負載變得明顯。圖8(c)所示為外加激勵對PEH裝置輸出功率的影響,與上面分析的一致,當壓電材料靠近振動收集端時,體系對加速度的響應特性更加明顯。因此,在不改變懸臂梁長度的前提下,適當增加振動收集端的壓電材料分布,能顯著提高PEH裝置的能量轉換效率和傳感靈敏度,同時,在相同振動模式下,體系最大功率處負載不隨壓電材料分布變化而變化,更有利于振動系統對外界能量的收集。

圖8 壓電材料分布對PEH的影響Fig.8 Effect of distribution of the piezoelectric material on PEH

3 驗證

為驗證有限元仿真對PEH結構影響特性分析的有效性和正確性,本文將理論分析結果與實驗室成果進行比較。文獻[16]設計的懸臂梁式PEH結構如圖9所示。

圖9所示的PEH裝置由傳感質量塊、雙壓電晶片、鋁支架和固定基座組成,其中雙晶壓電材料尺寸為20 mm×14 mm×0.16 mm,與表3所取的參數一致,為了減少二維模型對模擬結果的差異,本文設置面外尺寸為0.16 mm,與該裝置保持一致。鋁支架固定在一個模擬環境振動的電磁激振器上,雖然實際PEH結構(圖9(a))和圖9(b)中給出的(彈簧,質量,阻尼器)模型看起來不同,但在諧振頻率附近,該機電耦合模型可準確地描述PEH的振動行為。

圖9 PEH裝置示意圖[16]Fig.9 Piezoelectric generator[16]

圖10為本文有限元仿真結果與文獻[16]實驗室測試結果的比較,不難看出,文獻[16]測試得到的體系諧振頻率為66 Hz,最大輸出功率為0.57 mW,小于本文計算的結果,同時,文獻[16]得到的輸出功率在13.9 kΩ時達到最大0.58 mW,同樣小于本文的計算值。雖然較實驗測試數據有所偏差,但本文計算得到的響應特性變化趨勢與文獻[16]的結論相吻合。由于文獻[16]所取傳感質量塊的質量為0.76 g,而本文并未對質量定值,而是將其作為單位變量進行分析,因此本文設置的等效質量塊質量小于文獻[16],這也證實了質量分布對PEH的影響規律。為了減少模擬參數誤差對整體性的影響,本文的支撐架為結構鋼,而非文獻[16]所述的鋁。同時,由于本文所建立的模型為二維等效結構,無法得出與實驗完全一致的結果。綜上考慮,本文的計算結果可以較為有效地反映PEH結構參數對其能量轉換性能的影響特性,可為微結構能量轉換裝置的研究提供一定的設計指導和借鑒作用。

圖10 響應對比Fig.10 Comparison of response results

4 結論

本文通過有限元方法,探究了不同設計參數下振動頻率、外界負載和外部加速度激勵對壓電能量收集裝置輸出電性能的影響。仿真結果表明,傳感質量塊質量的增加伴隨著負載電壓和負載功率的增加,但保持質量塊體積一定時,改變其形狀可達到通過控制質心分布來調控PEH裝置的輸出響應;同時,隨著壓電材料厚度增加,系統的剛度增大導致壓電單元的應變降低,使得PEH裝置的最大輸出電壓和功率降低;壓電材料趨于振動收集側分布時會使體系的能量轉化效率明顯提升。在負載阻抗方面,改變PEH裝置的結構分布都會對系統最佳負載值有影響,然而,只改變壓電材料分布時,最佳負載值無明顯變化。對外部激勵方面,輸出電壓和輸出功率與加速度(外力)分別呈現出線性和二次函數關系,且隨著外部激勵的增加,輸出電壓和功率均增加,因此,可通過改變外力情況調控PEH的加速度響應范圍和靈敏性,由于本文模型具有較大的橫縱比,對縱向振動響應更為敏感。然而單方向振動模式并不能滿足實際振動環境的隨機性要求,因此,在單因素到多因素優化策略的同時,也需要從單維度到多維度設計,達到拓寬PEH裝置工作頻帶和提高其輸出穩定性的目的。