基于事件觸發(fā)機制的多飛行器有限時間協(xié)同制導方法

紀 毅，李俊賢，2，王 偉，閆華杰，2，范軍芳，2

(1. 北京信息科技大學自動化學院，北京 100192；2. 高動態(tài)導航技術北京市重點實驗室，北京 100192；3. 北京理工大學宇航學院，北京 100081；4. 無人機自主控制技術北京市重點實驗室，北京 100081)

0 引 言

具有“打擊面大、瞬時毀傷強、冗余高”等優(yōu)勢的多飛行器協(xié)同制導方法可有效應對實戰(zhàn)中單一飛行器“突防難、毀傷小、容錯低”的缺陷,是當前的研究熱點。一些傳統(tǒng)的研究通過分別對各個飛行器設計時間約束制導律的方法,達到“目標齊射”的效果。文獻[1]針對導彈自身速度時變條件下的攔截問題,基于偏置比例導引和平均速度法設計了飛行時間約束制導律。文獻[2]基于終端滑模理論,設計了一種無奇點的飛行時間約束制導律。文獻[3]針對導彈在大范圍機動運動中可能出現(xiàn)的視場丟失問題,將導引頭視場角為附加反饋項,實現(xiàn)了對攻擊時間及導引頭視場角的同時約束。然而,以上飛行時間約束制導律均需在飛行過程中實時精準地估計剩余飛行時間,亦需要據(jù)此設計期望終端命中時刻。在實際應用中,期望終端命中時刻須在發(fā)射前裝訂于各飛行器之中,故只能通過計算機仿真得出近似最優(yōu)值。此外,由于在時間約束制導機制下各個飛行器間不存在信息交流,各自不同的外部干擾對其時間約束性能帶來嚴峻挑戰(zhàn)。

時間約束制導機制的固有缺陷可通過研發(fā)具有實時通訊功能的多飛行器系統(tǒng)解決。當前的研究主要基于圖論與一致性原理,設計集中式或分布式多飛行器協(xié)同制導方法[4]。該方法主要可分為兩類:一種是引入?yún)f(xié)調(diào)變量并設計控制量,使得各飛行器的剩余時間達到一致[5];另一種是通過建立飛行器間的通信拓撲關系,結(jié)合多智能體一致性理論來解決多飛行器間狀態(tài)不一致的問題[6-7]。文獻[8]基于擴張觀測器和有限時間收斂控制理論,設計了一種適用于通信拓撲切換情況下的多飛行器一致性協(xié)同攔截方法。文獻[9]基于多智能體一致性算法和積分滑模理論,設計了一種三維時間角度約束制導律。文獻[10]研究了有向拓撲下的多導彈協(xié)同制導問題,提出了一種無需徑向速度測量的有限時間協(xié)同制導律。文獻[11]針對多高超聲速滑翔飛行器協(xié)同制導的問題,提出了一種兩階段一致性制導方法,在實現(xiàn)快速協(xié)同軌跡規(guī)劃的同時控制飛行時間和終端角度。然而,在上述一致性協(xié)同制導過程中,各飛行器需實時進行通信交流。在各自運動狀態(tài)不發(fā)生較大變動時,近似一致的信息將加重信道負荷,可能導致承載有效制導指令與運動狀態(tài)的信息傳遞受阻,進而影響一致性協(xié)同效果。

作為減少控制頻次和通信負載的有效途徑,事件觸發(fā)控制機制受到了廣泛的關注[12-13]。文獻[14-15]針對有向拓撲下的多智能體輸出共識問題,提出了基于事件觸發(fā)的控制協(xié)議,避免了智能體間持續(xù)不斷地低效信息交換。文獻[16]基于事件觸發(fā)函數(shù)和牽引控制設計了分布式控制器,適用于具有合作-競爭關系的異構(gòu)多智能體的一致性問題。文獻[17]考慮二階多智能體系統(tǒng)中各成員速度信息不可測和控制輸入有界的情況,通過引入輔助函數(shù)設計了一種基于事件觸發(fā)的一致性協(xié)議。文獻[18]針對具有事件觸發(fā)通信的不確定非線性系統(tǒng)的分布式一致性控制問題,提出了一種完全分布式自適應控制方案,并解決了執(zhí)行機構(gòu)失效問題。文獻[19]針對離散型多智能體系統(tǒng)狀態(tài)一致性問題,設計了一種基于事件觸發(fā)預測方案的控制方法,有效降低了控制與通信次數(shù)。將事件觸發(fā)機制引入多飛行器協(xié)同制導方法,具有以下優(yōu)勢:1) 制導控制指令并非連續(xù)生成,給執(zhí)行機構(gòu)留出足夠的執(zhí)行時間,適用于時間滯后系統(tǒng);2) 執(zhí)行機構(gòu)僅執(zhí)行有限次數(shù)的指令,可在達到協(xié)同制導目的同時,有效降低能量損失,理論上可提升射程;3) 復雜的戰(zhàn)場電磁環(huán)境難以保證通信系統(tǒng)長時間有效工作,此時,主動降低通訊需求可提升協(xié)同制導的可靠性。

此外,多飛行器協(xié)同制導系統(tǒng)各成員需在制導段調(diào)整狀態(tài)至趨同,并精準命中目標。通常,這一過程時間較短(通常不足1 min),有必要設計有限時間一致性方法。

為規(guī)避時間約束制導機制的固有缺陷,降低多飛行器間的通訊需求,提升協(xié)同制導的可靠性,在有限時間內(nèi)實現(xiàn)多飛行器的一致性,本文面向多飛行器高精度協(xié)同制導問題,設計了兩階段制導律,提出具有有限時間收斂功能的終端滑模面,構(gòu)建事件觸發(fā)機制下的有限時間一致性協(xié)議,主要貢獻與創(chuàng)新點如下:1) 傳統(tǒng)研究工作多基于二階多智能體動力學系統(tǒng)設計協(xié)同制導方法。本文通過引入中間變量和設計非奇異終端滑模面,將多飛行器協(xié)同制導動力學模型表述為一階多智能體系統(tǒng),簡化了設計過程。2) 傳統(tǒng)研究工作多采用均值一致性方法,為考慮有限時間收斂的需求。本文考慮實際執(zhí)行過程中的不同溝通方式,分別設計了集中式與分布式多飛行器有限時間一致性制導方法。3) 設計了基于事件觸發(fā)機制的多飛行器系統(tǒng)一致性制導方法。與傳統(tǒng)一致性協(xié)同方法相比,該方法在保證多飛行器運動狀態(tài)快速一致性收斂的同時,通過事件觸發(fā)機制降低了控制頻次和通信負載,提升了多飛行器系統(tǒng)的通信效率與可靠性。

1 多飛行器協(xié)同制導問題描述

首先闡述代數(shù)圖論與引理,其次建立了多飛行器系制導動力學模型,提出了兩階段制導方法,最后將協(xié)同制導問題轉(zhuǎn)化為帶有滑模面的一階多智能體系統(tǒng)一致性問題。

1.1 代數(shù)圖論與引理

(1)

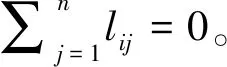
引理2[21].假設V(x)為定義于U?n上的C1型光滑正定函數(shù)。對于任意β1>0,β2∈(0,1),β3>0,存在定義于U?n的函數(shù)滿足,有函數(shù)不等式成立。此時存在數(shù)域U0?n滿足任意從其出發(fā)的V(x)均可在有限時間Treach內(nèi)到達V(x)=0的狀態(tài),且Treach≤ln(β3V1-β2(x0)+β1/β1)/β3(1-β2)。

1.2 多飛行器系統(tǒng)制導動力學模型

飛行器制導三維幾何場景如圖1所示。慣性坐標系定義為O-XYZ,O為坐標原點;M與T分別代表飛行器和靜止目標,R為飛行器與目標的相對距離,VM為飛行器速度,本文視為一常數(shù),且各飛行器速度相等;OA為飛行器速度方向,OB為飛行器縱軸方向,OC為視線方向,平面OAB垂直于平面OBC;θM為飛行器縱軸與飛行器速度的夾角,φM為視線與飛行器縱軸的夾角,θM與φM的方向互相垂直;θL與φL分別為彈目視線角在慣性系下的垂直分量與水平分量;σ為視線與飛行器速度方向夾角。將飛行器速度看作常值,彈目相對運動關系可由如下微分方程表示[21]：

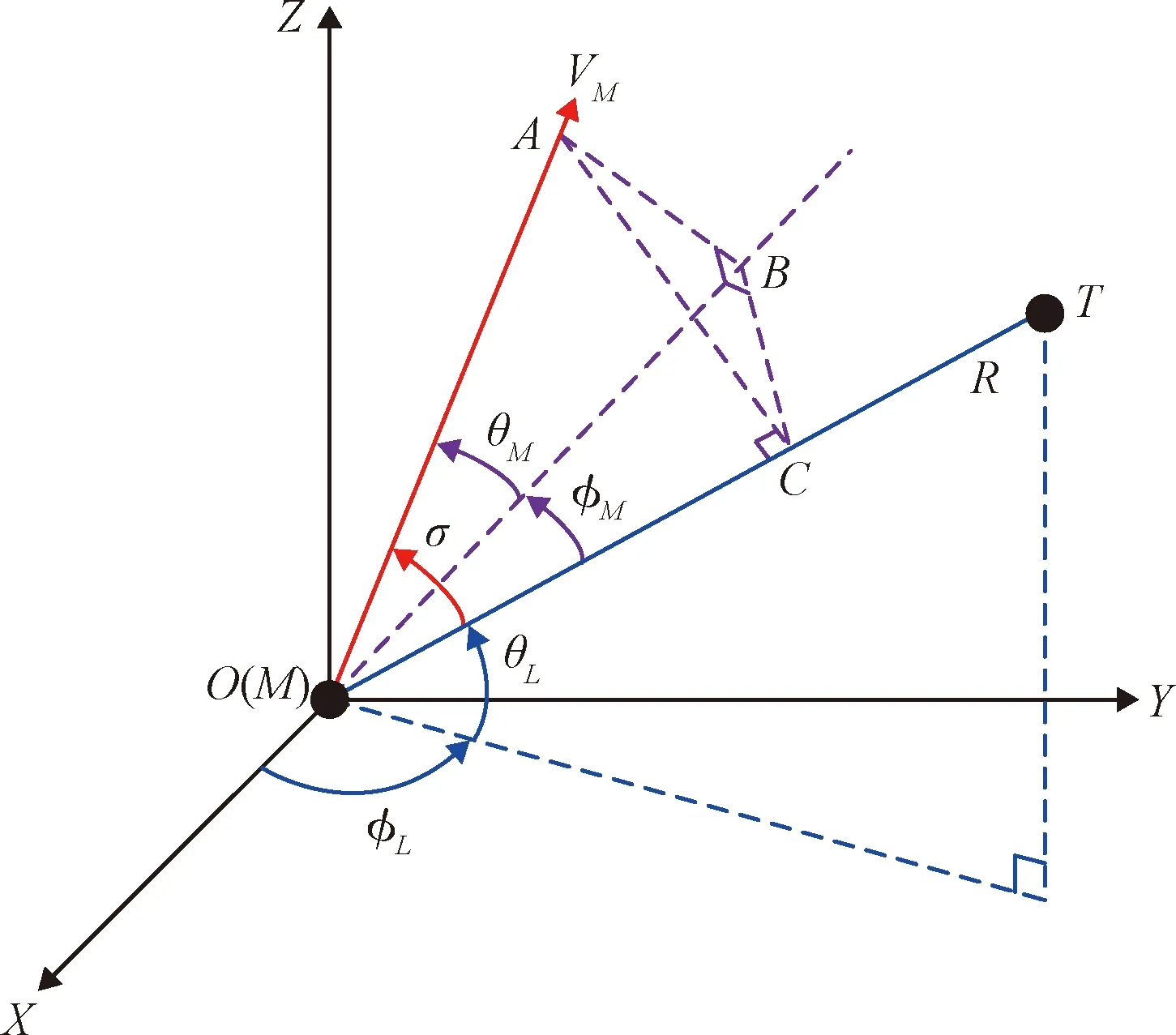
圖1 制導幾何關系圖

(2)

式中:az和ay分別表示飛行器俯仰和偏航加速度。

由圖1可得σ的計算公式為

σ=arccos(cosθMcosφM)

(3)

求式(3)的一階時間導數(shù),并將式(2)代入得

(4)

為規(guī)避對剩余飛行時間的實時精準估計,定義兩個輔助變量

(5)

求式(5)的一階時間導數(shù),并將式(2)～(4)代入,得

(6)

俯仰、偏航通道方向的控制量可寫作

(7)

式中:u為待設計的一致性控制協(xié)議。

將式(7)代入式(6),并考慮該成員在由n個個體組成的多飛行器系統(tǒng)內(nèi)的標號,可得

(8)

對于以上多飛行器系統(tǒng),其協(xié)同任務為:在某一終端時刻控制多個飛行器同時精確命中目標,并保證各飛行器狀態(tài)趨同。

1.3 兩階段制導方法

為完成多飛行器系統(tǒng)協(xié)同制導任務,本節(jié)設計兩階段制導方法。在第一階段通過基于有限時間一致性原理的制導方法,使式(8)中的兩個中間變量的一致性誤差收斂至零附近的一個小鄰域內(nèi),即

(9)

式中:εη>0和εj>0皆為微小常數(shù)。

第一階段僅實現(xiàn)了多飛行器系統(tǒng)內(nèi)各成員狀態(tài)趨同,并未實現(xiàn)制導。故第二階段引入三維比例導引制導律(10),以使各飛行器精確命中目標。

(10)

式中:λy和λz為彈目視線角分量,其一階時間導數(shù)可按式(11)求解

(11)

引理 3.[21]若多飛行器系統(tǒng)中各成員具有相同的導航比N,并且具有相同的初始彈目距離R(0),與初始夾角σ(0),那么這些成員的軌跡形狀相同。

引理3說明,各飛行器在第一階段在實現(xiàn)一致性后,各飛行器的軌跡形狀相同,在相同的速度下,必將在相同的時間命中目標。

第一階段僅約束了各飛行器的飛行時間和彈目視線角的數(shù)值,并未對交接點位置,彈目時間角方向、速度方向進行約束。因此,各飛行器的交界點位置,飛行方向并不相同。而引理3又進一步證明在實現(xiàn)一致性后,各飛行器的軌跡形狀相同。因此,二階段制導方法具有天然的避碰性,只在考慮各飛行器的體積時,系統(tǒng)內(nèi)各飛行器會在命中目標前的微小時間段發(fā)生碰撞。

1.4 問題描述

選取狀態(tài)變量x1=η,x2=ζ,則智能體i的動力學模型結(jié)合公式(8)可寫為

(12)

式中:xi(t)=[xi,1(t),xi,2(t)]T∈2是智能體i的狀態(tài)向量;ui(t)∈是智能體i的控制量。多智能體系統(tǒng)的網(wǎng)絡拓撲可表述為G={V,E,}。

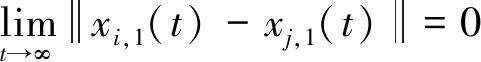
假設 1.多智能體系統(tǒng)的網(wǎng)絡通信拓撲形式為無向連通圖。

(13)

式中:k>0, 1

上述滑模面的收斂性質(zhì)可由引理4描述。

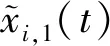
對式(13)求一階時間導數(shù),得

fi(t)+ui(t),i=1,2,…,n

(14)

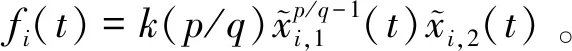
制導動力學模型(2)、二階一致性系統(tǒng)模型(8)、(12)與一階一致性系統(tǒng)模型(14)的轉(zhuǎn)換關系如圖2所示。引理4說明,通過控制滑模面(13),即可實現(xiàn)對系統(tǒng)(8)的二階一致性,進而實現(xiàn)多飛行器制導動力學一致性。

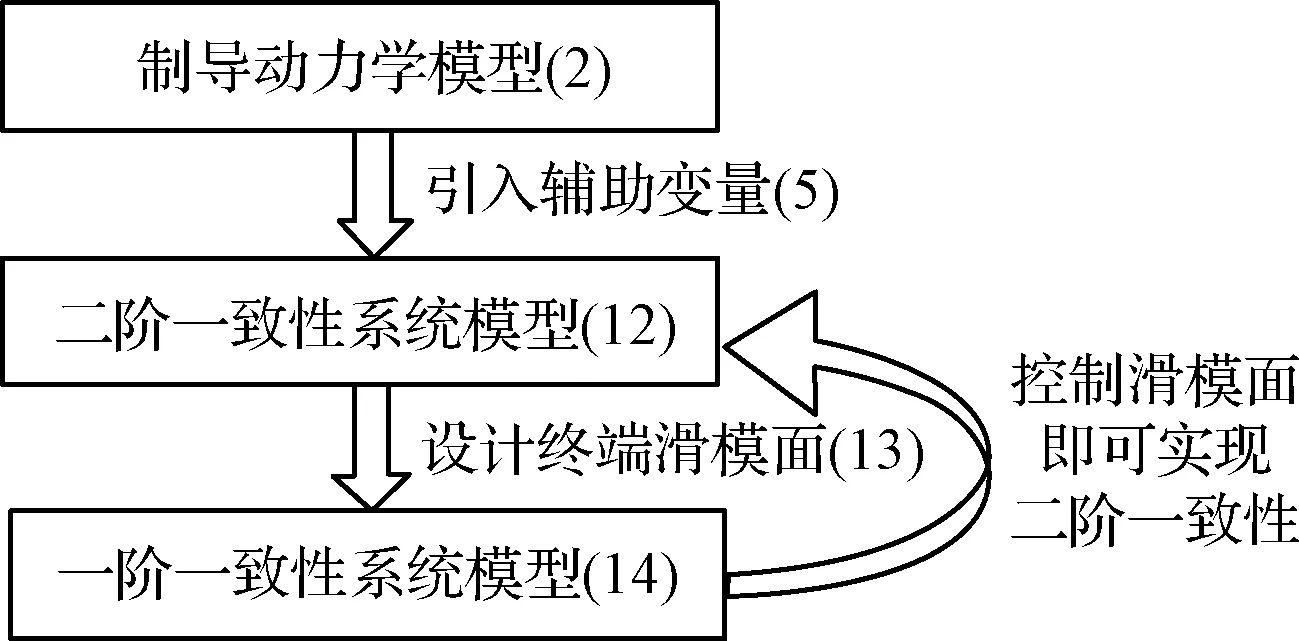
圖2 動力學模型轉(zhuǎn)換關系

假設 2.多智能體系統(tǒng)(12)符合Lipschitz條件,即存在一個正常數(shù)γ使得

|f(si(t),t)-f(sj(t),t)|≤γ|si(t)-sj(t)|

(15)

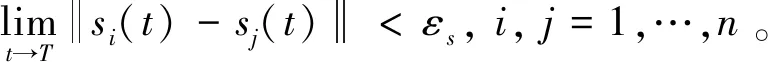
2 集中式事件觸發(fā)一致性制導律

首先對基于事件觸發(fā)的一致性制導律進行設計,其次通過構(gòu)造李亞普諾夫方程對多智能體系統(tǒng)的一致性進行分析,最后通過證明相鄰兩觸發(fā)點之間存在嚴格的正下界排除了Zeno現(xiàn)象。

2.1 制導律設計

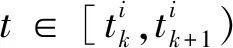
(16)

接下來,設計如下一致性協(xié)同方法

u(t)=-?1y(t)-?1yη1(t)

(17)

式中:?1>0, 0<η1<1為待設計參數(shù)。

將式(17)代入式(8),即可得到基于事件觸發(fā)機制的集中式一致性協(xié)同制導律。

2.2 一致性分析

采用如式(17)所示的基于事件觸發(fā)機制的平均一致性協(xié)同方法,多智能體系統(tǒng)(12)的一致性性能可用如下定理描述。

定理1.考慮同時滿足假設1、2的二階非線性多智能體系統(tǒng)(12),當γ≤?1λ2(L)時,采用基于事件觸發(fā)機制的集中式有限時間一致性協(xié)同方法(17)可使其狀態(tài)達到一致。

證明：定義二階多智能體系統(tǒng)(12)滑模面向量為s(t)=[s1(t),…,sn(t)]T,i=1,2,…,n,考慮以下李雅普諾夫函數(shù)

(18)

由引理1可知,拉普拉斯矩陣L為半正定矩陣,但當且僅當其特征向量為1時,L對應的特征值為0,此時多智能體系統(tǒng)(12)達成一致性,即si(t)=sj(t),i,j=1,…,n。故V1可用于評價系統(tǒng)(12)的一致性性能。

求(18)式的一階時間導數(shù),得

u(t))=-yT(t)(?1e(t)+?1y(t)+?1yη1(t)-f(t))

(19)

由假設2可得

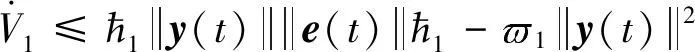
(fi(t)-fj(t))-?1(1-1)·

(20)

進一步整理得

(21)

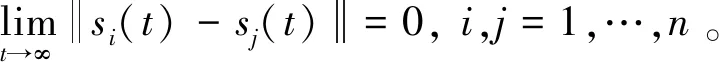
2.3 Zeno現(xiàn)象規(guī)避性分析

Zeno現(xiàn)象指在事件觸發(fā)控制中在有限時間內(nèi)發(fā)生無限次觸發(fā),即tk+1-tk<0。采用本章所述的集中式事件觸發(fā)一致性多智能體系統(tǒng)的Zeno現(xiàn)象規(guī)避性可總結(jié)為以下定理。

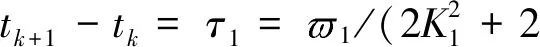
證明：定義(t)=e(t)/y(t),求其一階時間導數(shù)得

(?1η1(λN(L)V1(0))(η1-1)/2+?1+

(22)

進一步整理得

D+|(t)|≤(?1η1(λn(L)V1(0))(η1-1)/2+?1+

(?1η1(λn(L)V1(0))(η1-1)/2+?1+(t))·

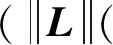
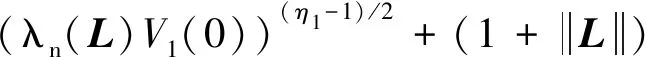
γ+(t))2=(K+(t))2

(23)

3 分布式事件觸發(fā)一致性制導律

本節(jié)面向多智能體系統(tǒng)(12)設計分布式事件觸發(fā)有限時間一致性制導律,設計流程與上一章相似。

3.1 制導律設計

定義分布式一致性誤差為

(24)

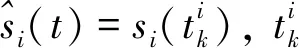
i=1,2,…,n

(25)

分布式事件觸發(fā)機制如式(26)所示。

(26)

設計如下一致性協(xié)同方法

(27)

其中,?2>0, 0<η2<1為待設計參數(shù)。

將式(27)代入式(8),即可得到基于事件觸發(fā)機制的分布式一致性協(xié)同制導律。

3.2 穩(wěn)定性分析

采用如式(27)所示的基于事件觸發(fā)機制的平均一致性協(xié)同方法,多智能體系統(tǒng)(12)的一致性性能可用如下定理描述。

定理3.考慮滿足假設1、2的二階非線性多智能體系統(tǒng)(12),當γ≤?2λ2(L)時,采用分布式事件觸發(fā)機制的一致性協(xié)同方法(27)可使其狀態(tài)達到一致。

證明：考慮以下李雅普諾夫函數(shù)

(28)

求(28)式的一階時間導數(shù),得

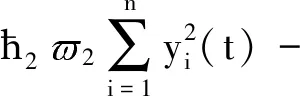
(fi(t)-fj(t))-?2(1-2)·

(29)

根據(jù)假設2,有

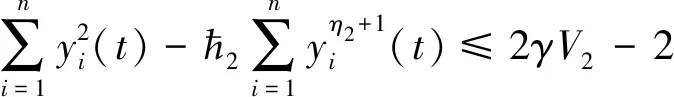
(30)

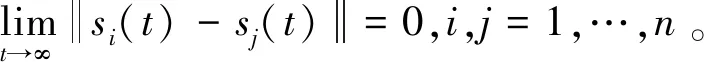
3.3 Zeno現(xiàn)象規(guī)避性分析

采用本章所述方法的分布式事件觸發(fā)一致性多智能體系統(tǒng)的Zeno現(xiàn)象規(guī)避性可總結(jié)為以下定理。

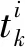
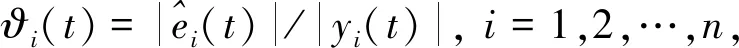
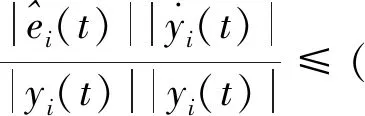
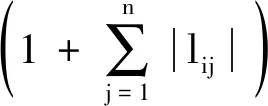
(Ki+?i(t))2

(31)

4 仿真校驗與結(jié)果分析

4.1 仿真設置

通過數(shù)值模擬證明了所提出的基于事件觸發(fā)的協(xié)同制導律的有效性,令5枚飛行器以相同的速度Vm=300 m/s攻擊靜止目標,飛行器加速度上限為amax=60 m/s2,比例導引段的導航比為N=5。飛行器間的通信拓撲關系如圖3所示,各飛行器的初始條件如表1所示,一致性制導算法中各參數(shù)如表2所示。

表1 仿真初始條件

表2 仿真參數(shù)

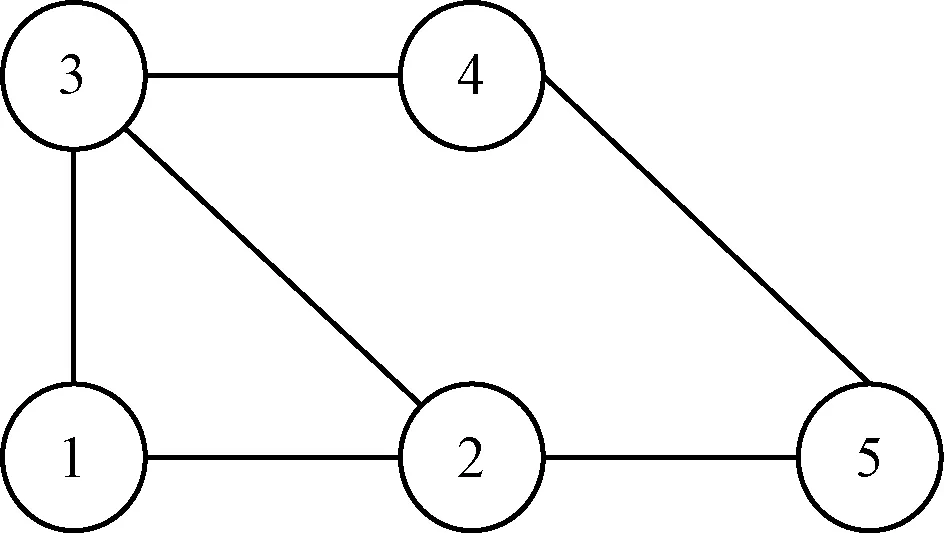
圖3 多飛行器通信拓撲關系

圖3所示多飛行器通信拓撲關系的鄰接矩陣和拉普拉斯矩陣為

(32)

4.2 集中式與分布式事件觸發(fā)制導仿真結(jié)果分析

集中式事件觸發(fā)有限時間一致性制導仿真實驗結(jié)果如圖4所示。圖4(a)為各飛行器的縱向、橫向加速度曲線。由圖4(a)可知,在該一致性制導方法的控制下,多飛行器系統(tǒng)中各成員均在約49.35 s時命中目標。圖4(b)形象地描述了兩階段制導方法的特點,各飛行器在24.23收斂至-0.537 4附近一微小鄰域,之后切換為比例導引制導律,直到命中目標。圖4(c)為各飛行器的事件觸發(fā)時刻。由上述仿真結(jié)果可以看出,在集中式事件觸發(fā)機制的作用下,各飛行器加速度指令在同一時刻觸發(fā)。

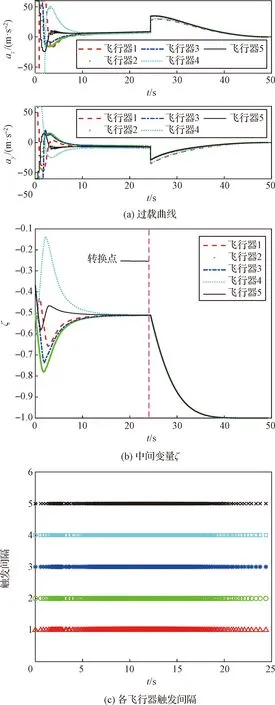
圖4 集中式事件觸發(fā)一致性制導仿真實驗結(jié)果

分布式事件觸發(fā)有限時間一致性制導仿真實驗結(jié)果如圖5所示。由上述仿真結(jié)果可知,在該一致性制導方法的控制下,多飛行器系統(tǒng)中各個成員均在約46.18 s時命中目標。各飛行器在20.32 s收斂至-0.546 9附近一微小鄰域,之后切換為比例導引制導律,直到命中目標。與集中式事件觸發(fā)機制不同,在分布式事件觸發(fā)機制控制下,制導指令由不同飛行器在不同時刻觸發(fā),觸發(fā)時刻如圖5(c)所示。

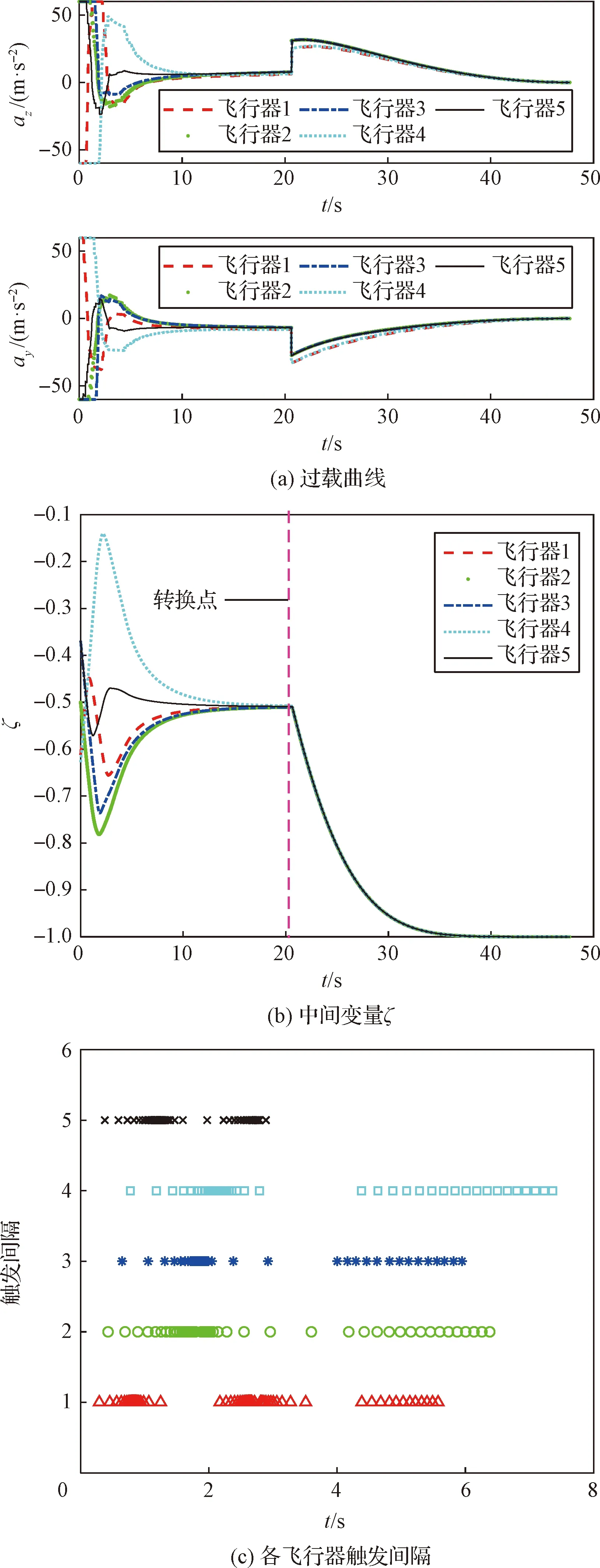
圖5 分布式事件觸發(fā)一致性制導仿真實驗結(jié)果

值得注意的是,仿真結(jié)果出現(xiàn)了初始階段飽和、抖振等現(xiàn)象,這是由滑模控制方法的固有特性引起的。初始階段系統(tǒng)軌跡偏離程度大,所需控制量大,故引起控制飽和現(xiàn)象。當系統(tǒng)狀態(tài)軌跡進入滑模面的另一側(cè)時,又會有相反方向的控制量,故出現(xiàn)抖振現(xiàn)象。但上述現(xiàn)象對系統(tǒng)可靠性的影響較低。由仿真結(jié)果可以看出,初始段過載加速度雖有飽和,但其界限為6g,此時飛行器處于滿舵狀態(tài),持續(xù)時間僅約1 s。集中式多飛行器系統(tǒng)的執(zhí)行機構(gòu)在10～25 s出現(xiàn)小幅抖振,但在事件觸發(fā)機制的調(diào)節(jié)下,保持了較低的頻率(5～10 Hz)。在分布式多飛行器系統(tǒng)中,由于事件觸發(fā)次數(shù)較低,抖振現(xiàn)象并未出現(xiàn)。

以上仿真結(jié)果說明,在本文提出的兩種事件觸發(fā)有限時間一致性協(xié)同制導方法控制下,多飛行器系統(tǒng)中各成員可在同一時刻完成制導任務。

4.3 與經(jīng)典均值一致性制導方法的對比分析

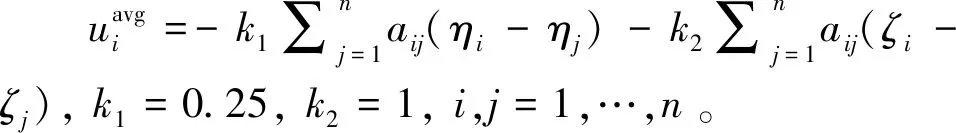
均值一致性協(xié)同制導仿真結(jié)果如圖6所示,圖6(a)(b)分別縱向過載與橫向過載、中間變量ζ。將以上仿真結(jié)果分別與圖4、圖5中對應部分進行對比,可以看出,各圖曲線趨勢相似,但圖6(a)中過載曲線平滑,不呈現(xiàn)階躍狀。這是因為在均值一致性協(xié)同制導過程中,制導指令連續(xù)產(chǎn)生,彈載計算機、通信系統(tǒng)、執(zhí)行機構(gòu)等組件須連續(xù)工作。而在基于事件觸發(fā)機制的協(xié)同制導過程中,上述元器件僅在圖4(c)、圖5(c)所示的觸發(fā)點工作即可,在減少控制次數(shù)、降低信道負載的同時,亦能保證良好的協(xié)同制導效果。

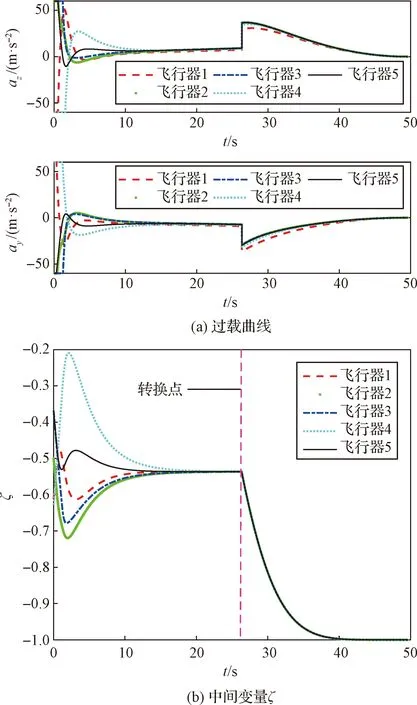
圖6 均值一致性協(xié)同制導仿真實驗結(jié)果

5 結(jié) 論

針對多飛行器系統(tǒng)時間約束下的協(xié)同制導問題,本文提出了集中式、分布式事件觸發(fā)有限時間一致性制導方法,具有以下優(yōu)勢:

1) 設計終端滑模面,將復雜的二階多智能體系統(tǒng)一致性問題降為一階,在保證一致性制導效果的同時,簡化的設計流程。

2) 設計了集中式、分布式事件觸發(fā)機制,降低了信道負載。

3) 面向短暫的制導窗口,設計了有限時間一致性方法,符合制導任務需求。