變壓應力條件下鐵鎵合金棒材高頻磁特性測試與模型構建

黃文美 陶 錚 郭萍萍 張偉帥 翁 玲

變壓應力條件下鐵鎵合金棒材高頻磁特性測試與模型構建

黃文美1,2陶 錚1,2郭萍萍1,2張偉帥1,2翁 玲1,2

（1. 省部共建電工裝備可靠性與智能化國家重點實驗室（河北工業大學） 天津 300130 2. 河北省電磁場與電器可靠性重點實驗室（河北工業大學） 天津 300130）

高頻大功率磁致伸縮換能器件的輸出特性與其所受的壓應力密切相關，施加一定的壓應力可以提高其核心元件磁致伸縮棒材的磁致伸縮系數，增大器件輸出功率，而不合適的壓應力會使得器件性能惡化。該文搭建了磁致伸縮材料高頻磁特性測試系統，測量了磁致伸縮材料鐵鎵合金棒材在不同激勵條件下（變壓應力、變勵磁頻率和不同磁場強度）的動態磁特性曲線。結果表明，當頻率與磁場強度一定時，隨著壓應力的增加，高頻磁特性中振幅磁導率減小、動態磁滯回線縱向變扁、磁能損耗減少。針對傳統磁滯模型無法計及壓應力影響的問題，在現有靜態J-A磁滯模型的基礎上，計及渦流損耗和剩余損耗，并采用分數階導數修正高頻渦流場表達式，建立了高頻動態磁滯模型，再引入壓應力相關項修正模型參數，得到與外施壓應力相關的改進高頻動態磁滯模型。將實驗數據與模型計算結果進行對比分析，結果表明，在變壓應力和高頻激勵條件下，模型計算結果與實測值吻合較好，最大誤差為5.86%，平均誤差為3.29%，驗證了模型的準確性與可行性。

鐵鎵合金棒材 壓應力 高頻磁特性 改進的磁滯模型

0 引言

磁致伸縮材料作為一種新型智能材料，能量密度高、耦合系數大，且兼具優良的應力靈敏性、磁致伸縮特性和力學性能，可廣泛應用于換能器、傳感器、精密機械控制等高新技術領域[1-2]。以磁致伸縮材料鐵鎵合金棒材為核心元件制成的高頻大功率磁致伸縮器件，需要棒材工作在一定的壓應力下以提高磁致伸縮應變、優化輸出特性；而不合適的壓應力會使得器件性能惡化。傳統的磁滯模型難以準確地模擬出材料在變壓應力條件下的磁特性[3]，因此，有必要建立一種計及變壓應力條件的鐵鎵合金棒材高頻動態磁滯模型。但是，一方面由于高頻條件下測試裝置磁能損耗大，加之鐵鎵合金磁導率低，以往的實驗平臺[4]無法達到較高的磁通密度，難以獲取建立模型需要的大量實驗數據；另一方面，靜態磁滯模型未考慮到鐵磁材料的高頻渦流損耗與剩余損耗，經修正后的動態模型[5]忽略了高頻趨膚效應對材料內部磁場分布的影響，不適用于研究材料高頻磁特性；此外，由于鐵鎵合金材料具有應力敏感性，在施加壓應力時勢必會引起棒材內磁場變化，一般的方法是在棒材內部有效場計算中引入應力相關項[6]，但這會引起模型求解復雜化。

目前，對于磁性材料的磁滯特性模型研究主要分為兩類：一是基于磁滯理論建立的Preisach模型、神經網絡磁滯模型，這一類模型通過純數學手段描述材料磁滯特性；二是基于磁疇理論建立的物理與數學相結合的J-A磁滯模型、自由能模型。其中，J-A磁滯模型是一種依據磁化機理建立的標量磁滯模型，具有穩定、準確、模型參數較少、物理含義明確，以及磁滯回線形狀、大小與模型參數緊密相關等優點，因此在鐵心磁滯建模領域得到了廣泛應用。

文獻[7]在變溫條件下測試電工鋼材料磁滯回線并提取J-A模型相關參數，研究電工鋼材料的溫度依賴性，通過將各參數表示為溫度的函數，將熱效應納入現有模型，簡化了模型識別過程。文獻[8]基于磁彈性效應和J-A模型理論建立外施應力下的鋼材磁特性模型，研究應力對鋼材磁滯回線的影響，并采用Powell算法確定模型參數的應力依賴性，研究結果可較為準確地評估鋼材所受應力。文獻[9]基于考慮機械應力和晶體織構效應的多尺度模型，提出了J-A模型計及壓應力條件下的優化形式，采用多尺度方法修正無磁滯磁化強度an和損耗系數，并利用實驗結果進行參數識別，所得出的優化模型與實驗結果吻合度較高。但上述研究建立的模型均為靜態磁滯模型，僅適用于描述靜態、準靜態條件下材料的磁滯特性。

文獻[10-11]基于能量守恒定律，考慮高頻條件下電工鋼材料的渦流損耗和剩余損耗，建立了計及直流偏置時變壓器鐵心材料磁化特性的高頻動態J-A模型，模型計算結果具有通用性，但該研究沒有研究變壓應力條件下電工材料的磁滯特性。文獻[12]通過引入頻率、壓應力相關項對J-A模型參數進行修正，較為準確地模擬出頻率、壓應力對變壓器鐵心硅鋼片-曲線的影響。但由于該研究所基于的磁滯模型為靜態模型，且實驗測試頻率小于1 kHz，無法用于準確地模擬更高頻率（如超聲應用）勵磁條件下磁致伸縮材料的磁滯特性。

本文首先基于磁損耗理論搭建磁致伸縮棒材高頻磁特性測試平臺，測量磁致伸縮材料鐵鎵合金棒材在不同應力和勵磁條件下的動態磁特性曲線并分析磁參數的變化趨勢；然后在現有靜態J-A磁滯模型的基礎上，基于損耗分離理論建立計及渦流場和剩余損耗場的鐵鎵合金棒材動態J-A模型，采用分數階導數修正高頻渦流場表達式，使建立的動態磁滯模型適用于高頻條件；最后基于實驗測試數據并利用Matlab編寫的J-A模型參數辨識程序求得不同壓應力條件下的模型參數值，分析壓應力對模型參數的影響，將各參數看作外施壓應力的多項式函數，得到與外施壓應力相關的改進高頻動態磁滯模型。

1 測試平臺搭建與實驗結果分析

1.1 高頻磁特性測試平臺搭建

為獲取高頻變壓應力條件下鐵鎵合金棒材磁特性相關數據，本文設計了一種棒狀鐵鎵合金高頻磁特性測試裝置。由于隨著頻率的升高，測試裝置磁路損耗增加、繞組趨膚效應和鄰近效應影響加劇，導致勵磁線圈等效阻抗增大、勵磁電流難以施加，加之鐵鎵合金棒磁導率低，使得被測棒材內部難以獲得數值較高的磁通密度。為了解決上述問題，首先，基于磁損耗理論選取磁心損耗較低的高頻導磁材料搭建磁路；然后，以提高電磁轉化效率為目標，采用受高頻趨膚效應和鄰近效應影響小的利茲線繞制勵磁線圈；最后，依據串聯諧振原理進行阻抗匹配。測試裝置整體采用四線圈結構，以提高勵磁磁場大小，此外，為使壓應力可傳遞到棒材上，上極頭被設計為可上下自由活動。

本實驗所搭建的測試系統原理如圖1所示，測試平臺可完成高頻磁場施加、壓應力加載、信號檢測及數據處理功能。測試平臺實物如圖2所示。

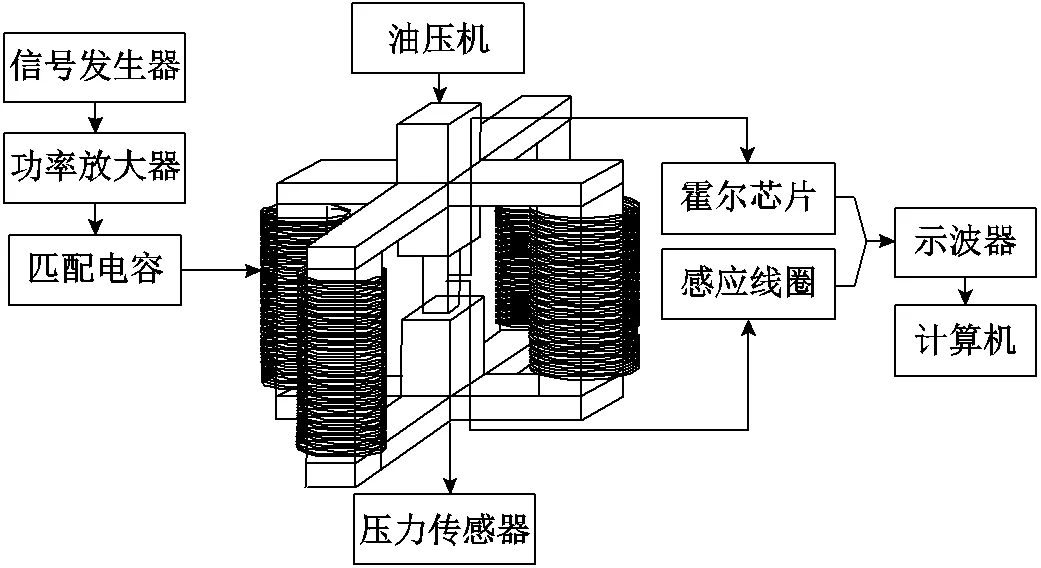
圖1 測試系統原理

圖2 測試系統實物

1—功率放大器 2—信號發生器 3—示波器 4—磁通計 5—油壓機 6—高頻磁特性測試裝置（含磁路、勵磁線圈、匹配電容、壓力傳感器） 7—霍爾芯片電源

Fig.2 Physical view of the test platform

高頻磁場施加由信號發生器、功率放大器、匹配電容和所設計的高頻磁特性測試裝置完成。通過功率放大器放大并輸出由信號發生器生成的高頻電壓，通過匹配電容加載到勵磁線圈上以產生高頻磁場，經高頻導磁材料制成的磁路導入被測棒材中。應力的施加由油壓機、壓力傳感器完成。通過油壓機給棒材施加一定的壓應力并在壓力傳感器上讀取壓應力數值。

平臺采用感應線圈法和A1321LUA型霍爾芯片完成信號檢測，當磁場改變時，纏繞在被測棒材上的感應線圈中的磁通量也會隨之變化，由法拉第電磁感應定律得

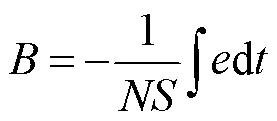
式中，為磁通密度；為感應線圈匝數；為棒材橫截面積；為感應電壓；為時間。

霍爾芯片用來采集棒材上的磁場強度，由霍爾效應可知

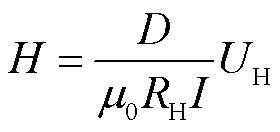
式中，為磁場強度；為芯片電流；H為芯片感應電壓；H為霍爾系數；為芯片厚度；0為真空磁導率。

感應線圈與霍爾芯片輸出的信號由示波器與磁通計采集，并將數據導入計算機中，通過Matlab軟件繪制、、和曲線（為磁化強度）。

1.2 變壓應力下高頻磁特性測試結果分析

實驗測試樣品為疊堆結構鐵鎵合金棒材，疊片厚度為1 mm、高度為20 mm，棒材橫截面尺寸為10 mm×10 mm。考慮到棒材磁特性與材料所受壓應力、頻率、棒材上磁場強度密切相關，本文采用控制變量法分別在不同壓應力、頻率、磁場強度下進行大量測試，結合鐵鎵合金棒材在水聲頻段的具體應用背景，實驗測試壓應力范圍為0～60 MPa，頻率范圍為1～9 kHz，調節外加磁場，控制棒材上磁場強度的范圍為1 000～6 000 A/m，以此來繪制出變壓應力條件下鐵鎵合金棒材在不同頻率和不同磁場強度下的動態磁特性曲線。

頻率=5 kHz、磁場強度=5 000 A/m時，不同壓應力條件下鐵鎵合金的曲線如圖3所示。可知當磁場強度一定時，隨著外施壓應力提高，動態磁滯回線縱向變低，產生的磁通密度幅值降低，剩磁減小，磁能損耗降低。由此可見，外施壓應力對材料磁疇壁移動和磁疇轉動等行為有明顯影響，這些影響可通過J-A模型參數變化體現出來。

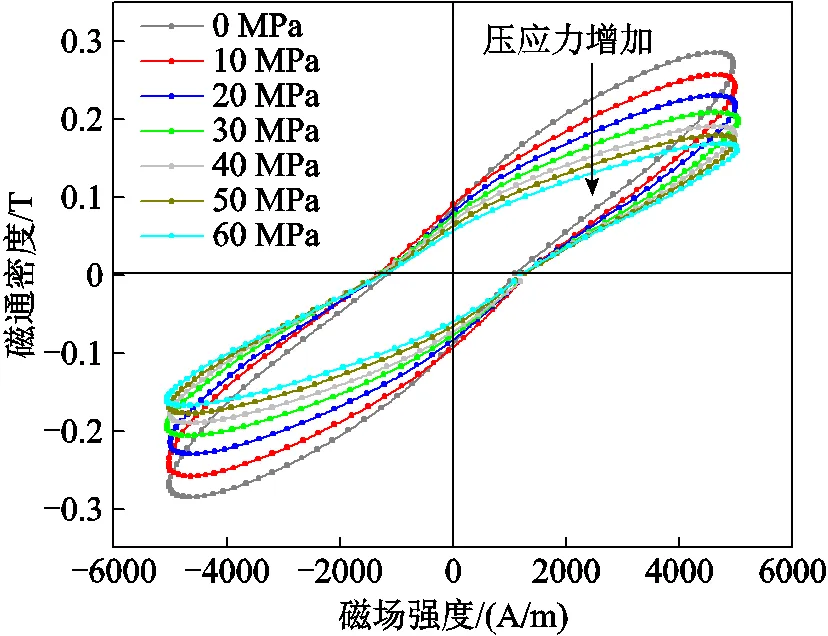
圖3 不同壓應力下的動態磁滯回線

磁導率是表征材料動態磁特性的重要參數，圖4所示為鐵鎵合金棒材在5 kHz頻率下、磁場強度為5 000 A/m時，樣品的振幅磁導率及實、虛部磁導率隨壓應力變化的曲線。從圖4中可以發現，在外施壓應力從0 MPa變化到60 MPa的過程中，樣品的振幅磁導率及實、虛部磁導率隨壓應力的增大而減小，該樣品振幅磁導率減小了40.89%（由0 MPa時的45.65 H/m下降到60 MPa的26.98 H/m）。在磁場強度一定時，隨著振幅磁導率減小，鐵鎵合金棒材中產生的磁通密度幅值m相應減小，回線縱向變低，棒材的剩磁和損耗減少。

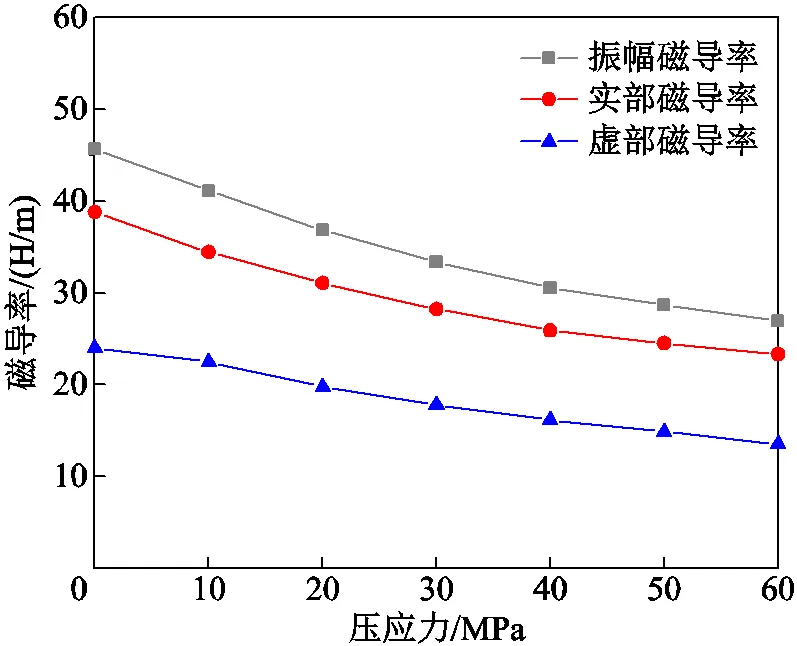
圖4 振幅磁導率和實部、虛部磁導率與壓應力關系

剩磁表示磁場減弱到零后，鐵鎵合金棒材中所剩的磁通密度大小，材料的磁能損耗則與磁滯回線的面積相關。圖5所示為鐵鎵合金棒材在頻率為5 kHz下、磁場強度為5 000 A/m時，剩磁r及單位質量磁能損耗隨外施壓應力變化的曲線。從圖5可以發現，隨著外施壓應力的增加，剩磁減少了38.04%（由0 MPa時的0.092 T減小到60 MPa時的0.057 T），磁能損耗減少了41.55%（由0 MPa時的862.21 W/kg降至60 MPa的503.96 W/kg），磁滯效應減弱。

由以上實驗結果分析可知：隨著壓應力的增加，鐵鎵合金棒材磁導率減小，導磁性下降，材料的磁化過程越來越困難，但施加較大的壓應力可以在磁場強度一定的情況下降低鐵鎵合金棒材磁損耗，同時剩磁降低，磁滯效應減弱。因此，為準確地描述鐵鎵合金棒材高頻磁特性隨外施壓應力改變而變化的情況，需要建立一種計及壓應力變化的高頻動態磁滯模型。

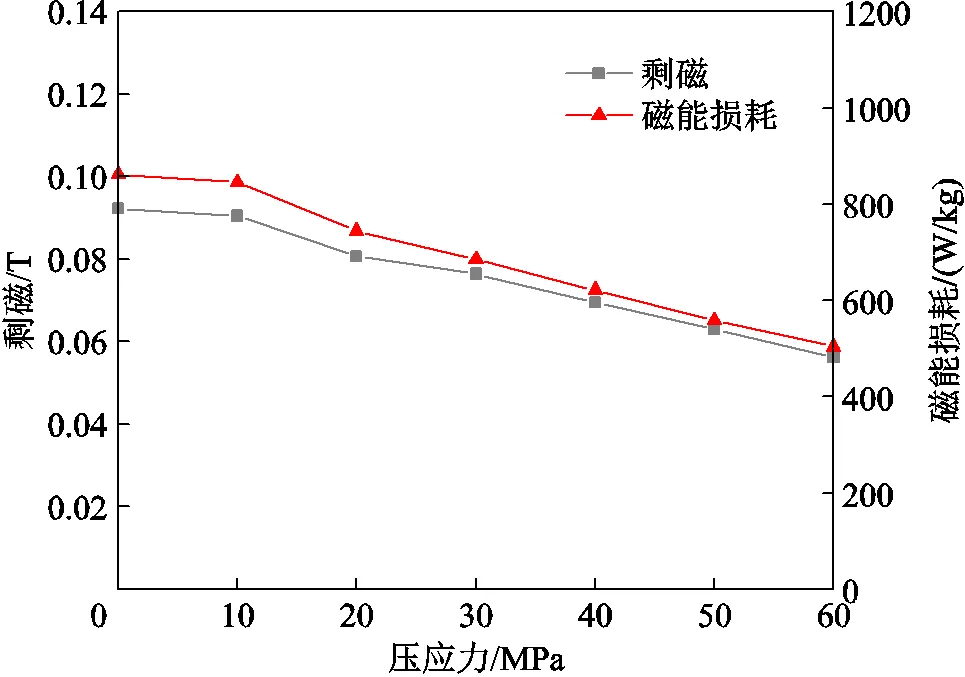
圖5 剩磁、磁能損耗與壓應力關系

2 經典J-A模型理論

2.1 靜態J-A模型

經典的J-A模型將磁疇磁化過程分解成不可逆分量irr和彈性分量rev，采用朗之萬函數描述磁化強度與磁場強度之間的關系。在恒溫條件下模型可表述為

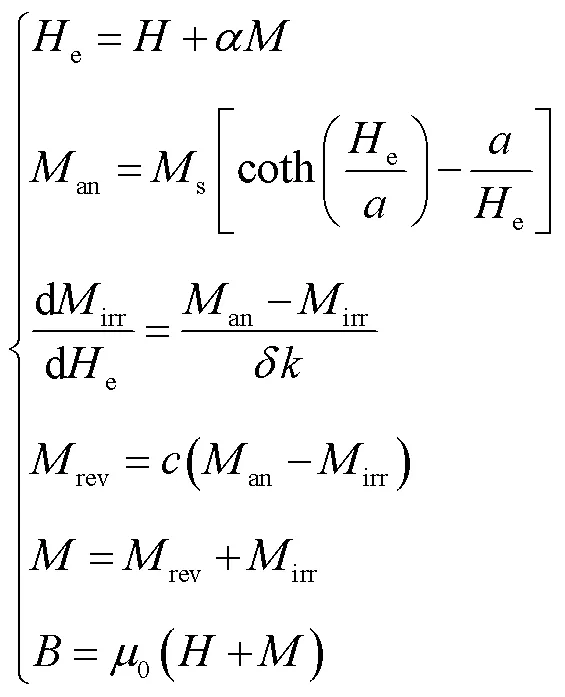
式中，an為無磁滯磁化強度；s為飽和磁化強度；e為有效磁場強度；為耦合系數；為磁疇壁相互作用系數；為損耗系數；為不可逆損耗系數；=sign(d/d)，sign為符號函數。

磁化強度與磁場強度的微分方程為

其中s、、、、為模型待定參數，數值確定后通過求解J-A模型便可繪制相應的-曲線。

2.2 計及壓應力影響的靜態J-A模型

當鐵磁材料受到機械應力時，內部有效場e-σ可分解為不計壓應力作用時的有效磁場e、應力退磁項M和附加機械應力場，材料中有效磁場表達式[13]可改寫為

其中

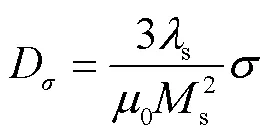
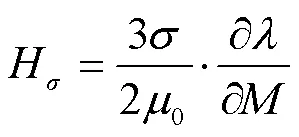
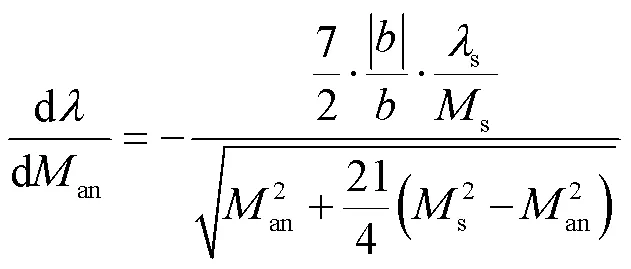
式中，e-σ為計及壓應力影響的材料內部有效磁場強度；M為應力退磁項；s為飽和磁致伸縮系數；為磁滯伸縮系數；為磁彈性耦合常數。

在2.1節所述的靜態J-A模型的基礎上，考慮壓應力影響下的模型修正為

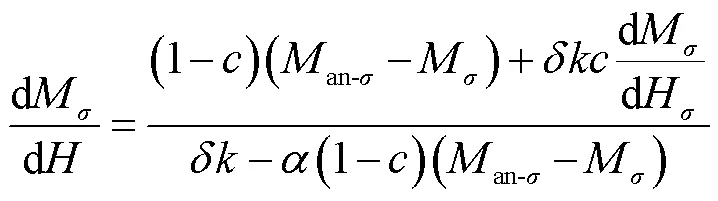
式中，an-σ為含e-σ的無磁滯磁化強度；為含e-σ的動態磁化強度。

3 計及壓應力影響的高頻動態J-A模型

3.1 高頻動態J-A模型

根據磁性材料的損耗分離理論，總損耗由磁滯損耗hys、渦流損耗ed與剩余損耗ex三部分組成，即

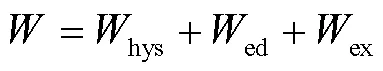
在靜態、準靜態條件下，材料內部磁場的趨膚效應可以忽略，可將疊片內部磁場視為均勻磁場；此外，經典的渦流損耗取決于材料厚度與電導率，所以假設它獨立于機械應力，渦流損耗與渦流場的表達式分別為

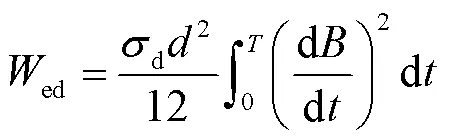
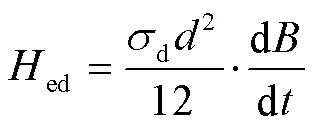
式中，d為材料電導率；為材料疊片厚度；為磁化周期。

但隨著頻率的升高，趨膚效應影響加劇，材料內部磁場強度呈現出表面高、中心低的特點，使得未考慮磁場分布影響的傳統方法計算值與實驗值之間誤差過大，因此引入R-L型分數導數，對高頻渦流場進行修正。R-L型分數導數具體形式[14]為

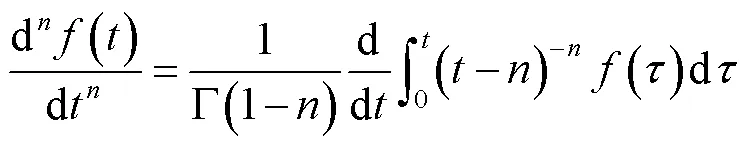
式中，非整數階的取值范圍為(0, 1)；Γ(·)為歐拉伽馬函數。

R-L型分數階導數為微分算子形式，自初始時刻0到當前時刻的整個過程都可以考慮變量的影響，相較整數階，分數階更適用于冪律性、非局部等復雜情況[15]。由于非整數階可以為任意非負實數，因而采用分數微分算子描述的渦流損耗值表達式對頻率具有依賴性，可保證高頻渦流損耗的計算精度。

將傳統渦流場表達式與R-L型分數階導數相結合，推導出改進的渦流場表達式[16]為

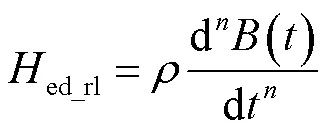
式中，為阻尼系數。相應的渦流損耗表達式為

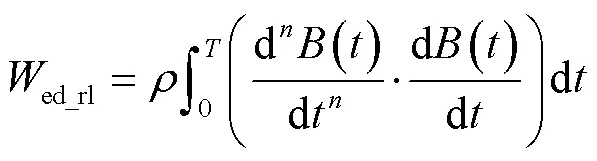
由于趨膚效應對剩余損耗幾乎沒有影響[17]，在此只考慮修正渦流損耗項。剩余損耗與剩余損耗場可分別表示為

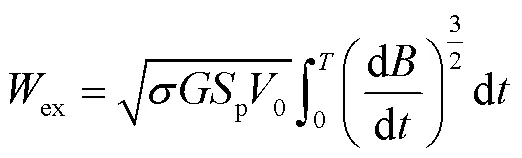
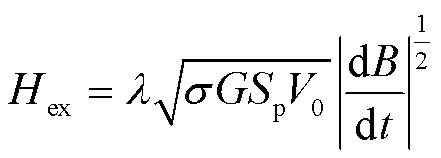
式中，p為疊片截面積；=0.137 5；0為統計參數，可利用總損耗和渦流損耗計算值的差值與頻率的1/2次冪之間的線性關系取得[18]。

由此，總損耗可以進一步表示為

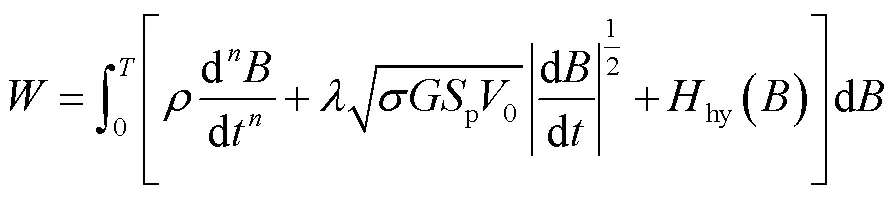
式中，hy()為可由靜態J-A模型獲取的磁滯損耗對應磁場強度分量。要確定參數與的值，首先，通過將參數的值從1逐漸減小（步長設置為0.01）來進行調整；然后，固定參數不變，調整參數，直到采用式（18）計算的總損耗值接近實際測量的損耗值[19]。此處取=0.98、=0.142。

將改進渦流場ed與剩余損耗場ex的表達式代入關于有效場的表達式（3）中，得到含動態場的有效磁場強度為

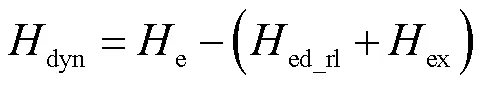
結合式（4）得到動態磁化微分表達式為

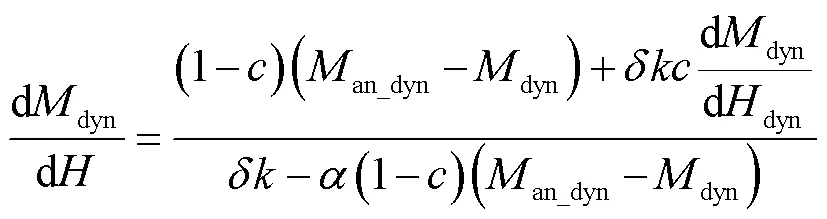
式中，an_dyn為含dyn的無磁滯磁化強度；dyn為含dyn的動態磁化強度。

3.2 以擬合參數法計及壓應力影響的高頻磁滯模型

要建立高頻條件下計及外施壓應力的鐵鎵合金動態J-A磁滯模型，需要將2.2節中表達式較為復雜的e-σ與動態磁化微分表達式（20）相結合，但這會引起模型求解計算量增大；此外，還需準確地測量磁致伸縮系數，增加實驗難度。因此，本文提出了基于式（20）的鐵鎵合金棒材高頻變壓應力模型的簡便建模方法：將實測數據繪制成曲線，然后采用混合粒子群算法，對J-A模型的五個參數（s、、、、）進行辨識，選取相應的擬合多項式，按照模型參數隨壓應力變化的規律，將J-A模型各個參數擬合為壓應力的多項式函數，建立計及壓應力影響的變系數高頻磁滯模型。

要獲取J-A模型參數值，需要對不同壓應力下鐵鎵合金棒材磁滯回線實驗樣本數據進行參數辨識。公式法采用迭代運算，盡可能減小矯頑力c、剩磁r、矯頑力點磁化率c、無磁滯磁化曲線的初始磁化率m等特殊點的計算誤差，從而得到最優參數值，但此方法對初值及迭代次序敏感且精度不高；擬合法則以實測磁滯回線與計算磁滯回線吻合度最大為目標，通過優化算法實現參數的辨識，過程簡單、執行效率高。本文采用將遺傳算法中雜交的概念應用到粒子群算法中的混合粒子群算法，以計算的磁滯回線與實驗獲得的磁滯回線之間的磁場強度的方均根誤差作為目標函數，實現J-A模型的參數辨識，流程如圖6所示。

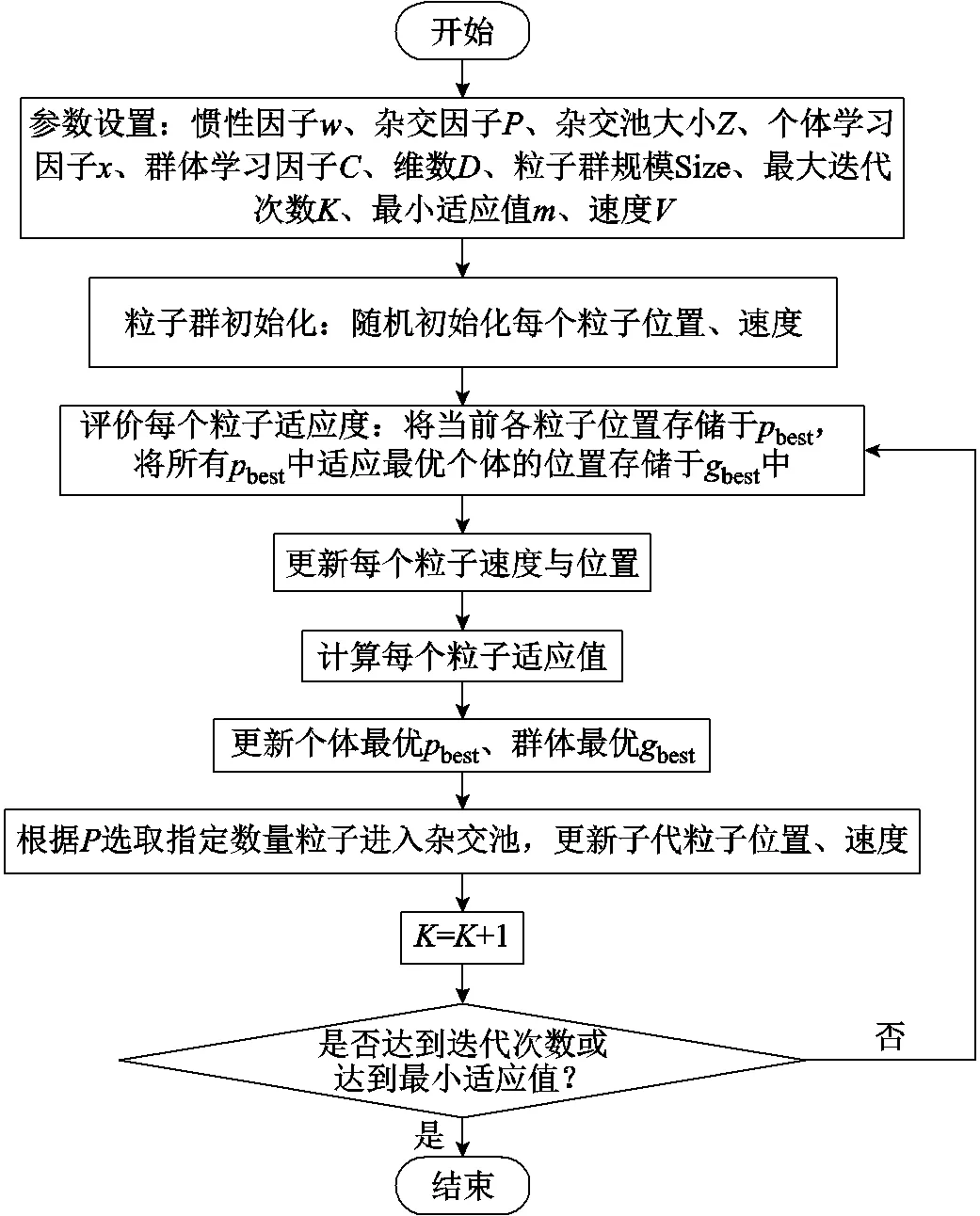
圖6 J-A模型參數辨識流程

將不同外施壓應力下（0～60 MPa）鐵鎵合金棒材曲線數據導入上述辨識程序中，進行參數辨識，結果表明：由于鐵鎵合金棒材的應力敏感性，在受到外施壓應力作用時，棒材磁滯特性勢必受到影響，反映磁滯回線形狀、面積的J-A模型參數（s）[20-21]也隨之變化。相應的變化規律如圖7所示。

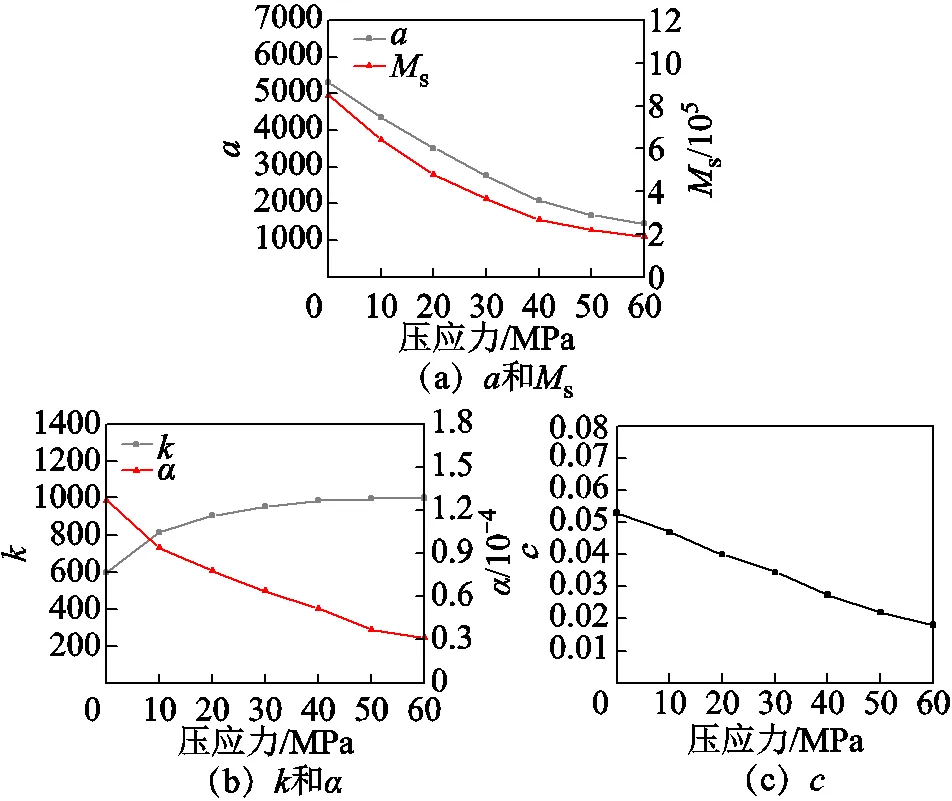
圖7 模型參數的壓應力相關性

在此將模型各參數看作壓應力的多項式函數，對于參數s、宜用關于外施壓應力的三次多項式進行擬合，其通式可表示為

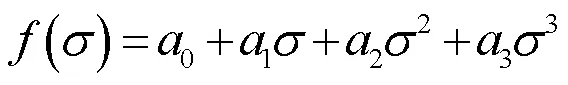
式中，0～3為多項式系數。而參數的變化趨勢可近似看作直線，采用一次多項式擬合，其通式可表示為

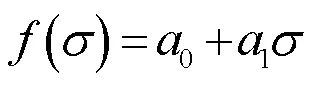
則模型參數表達式見表1。

表1 模型參數表達式

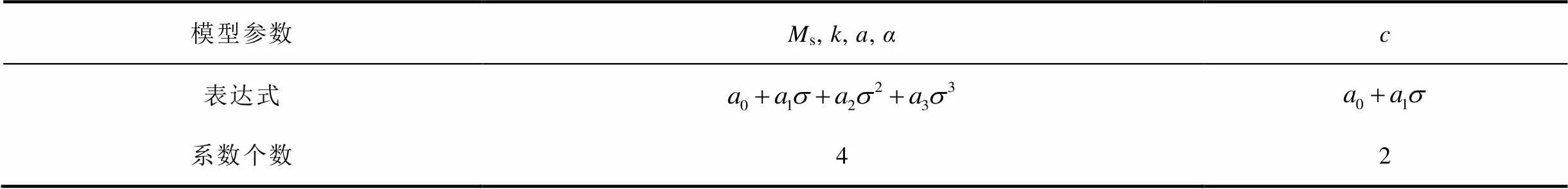
Tab.1 Model parameter expressions

其中，各參數的邊界條件：與的取值范圍為[0.2c, 5c]；取值范圍為[0,tip/tip]，其中tip和tip分別為頂點磁場強度和頂點磁化強度[22]；的取值范圍為[0, 1]。在邊界條件給定的情況下，采用控制變量法，給定頻率與磁場強度，改變外施壓應力（本文的測試頻率為1～9 kHz，磁場強度范圍為1 000～6 000 A/m，壓應力范圍為0～60 MPa），將實驗數據導入混合粒子群算法辨識程序，將各個參數擬合為壓應力的多項式函數后，相應的多項式系數記錄于表2。

表2 修正模型相關參數值

Tab.2 Correction of model-related parameter values

至此，通過混合粒子群算法對有限的實驗數據進行參數辨識，將J-A模型各參數擬合為壓應力的多項式函數，代入式（20）中，建立了計及壓應力影響的變系數高頻磁滯模型。根據各參數隨壓應力的變化規律，還可將模型推廣至更寬的應用范圍內。

3.3 變壓應力下高頻磁滯模型的驗證

為了驗證所建立的計及壓應力變化的高頻動態J-A模型的準確性，在給定工作條件下（不同頻率、磁場強度、外施壓應力）測試鐵鎵合金棒材的磁滯特性。通過控制變量法分別繪制不同頻率、磁場強度和外施壓應力下的實測曲線，與模型計算結果進行對比，如圖8～圖10所示。

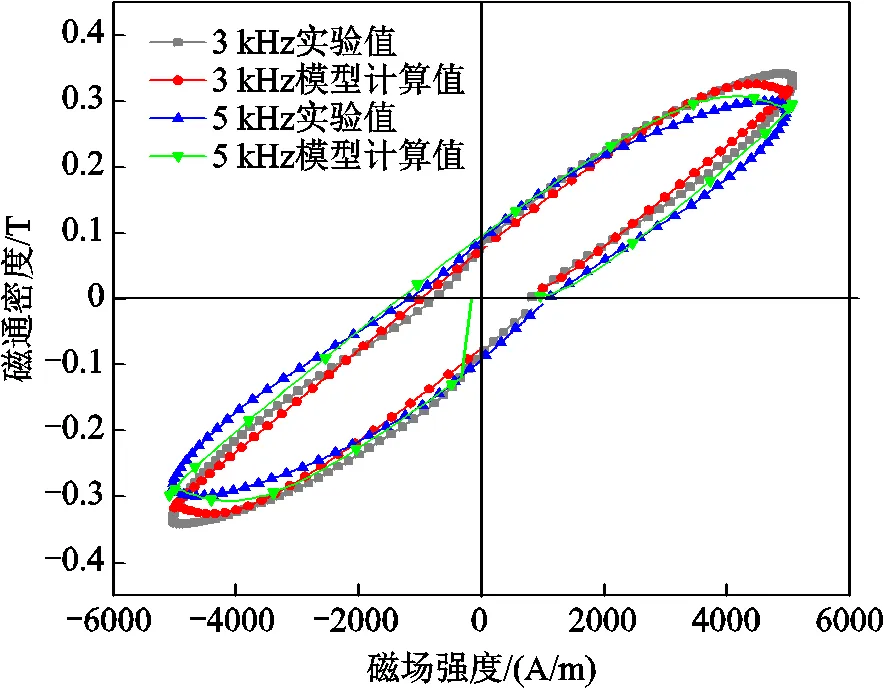
圖8 不同頻率下磁滯回線實驗值與模型計算結果（H=5 000 A/m, σ=0 MPa）

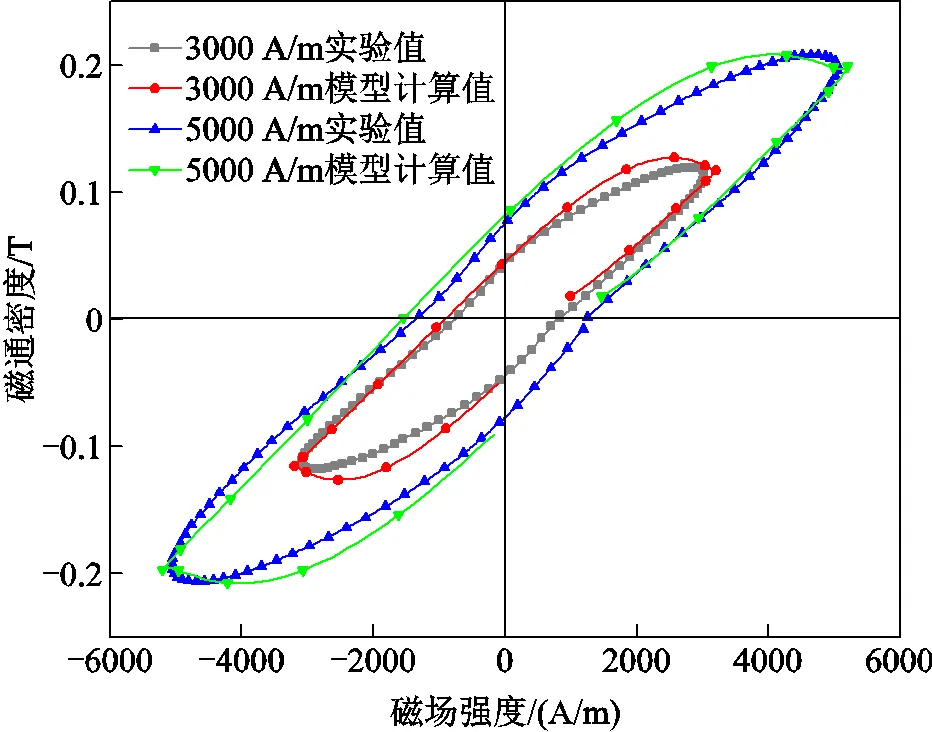
圖9 不同磁場強度下磁滯回線實驗值與模型計算結果（f =5 kHz, σ=30 MPa）

為了表示模型的精確度，定義誤差量為

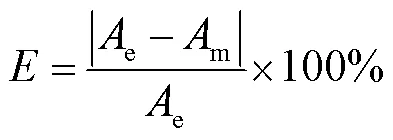
式中，Ae為實驗測量的B-H曲線面積；Am為模型計算結果所得B-H曲線面積。

圖11所示分別為在磁場頻率為1～9 kHz（= 5 000 A/m、=0 MPa）、磁場強度為1 000～6 000 A/m（=5 kHz、=30 MPa）和壓應力為0～60 MPa（= 5 kHz、=5 000 A/m）的磁能損耗實驗結果和模型計算結果的誤差量。由于采用動態J-A磁滯模型并引入分數階導數修正渦流損耗場，在高頻激勵下（=1～9 kHz），模型計算結果頻率適應性較好，最大誤差量為6.88%，平均誤差量為4.71%。此外，改進后的動態模型能反映出損耗量在磁場強度大小變化時的改變，在頻率、外施壓應力恒定（=5 kHz、=0 MPa）時，不同磁場強度下（=1 000～6000 A/m）所繪制的磁滯曲線較貼近實驗值，最大誤差量為6.99%，平均誤差量為4.28%。在磁場頻率、磁場強度恒定時（=5 kHz、=5 000 A/m），改變外施壓應力條件下（=0～60 MPa），考慮到外施壓應力對鐵鎵合金棒材磁特性的影響，將模型參數改寫為外施加壓應力的多項式函數，提高了計及壓應力條件下的模型計算與實驗結果的吻合性，最大誤差量為5.86%，平均誤差量為3.29%。

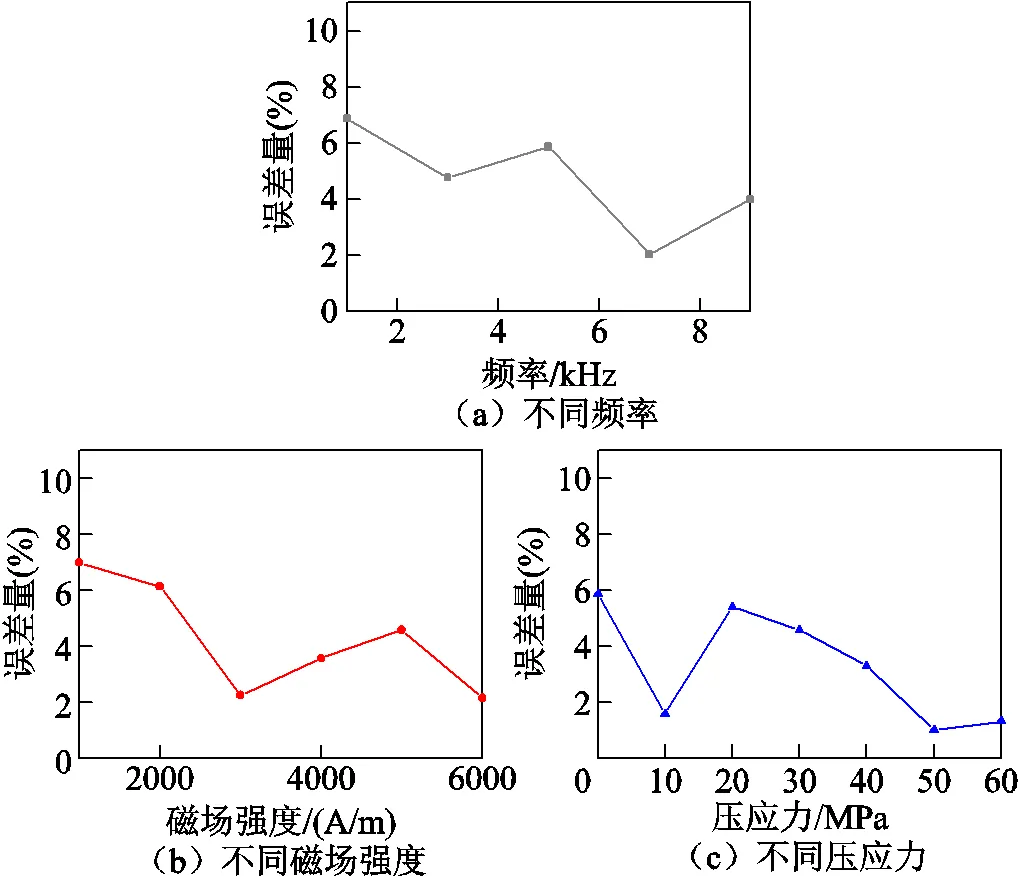
圖11 不同頻率、磁場強度和壓應力下模型誤差量

4 結論

本文搭建了外施壓應力可控的磁致伸縮棒材高頻磁特性測試平臺，分析測試了不同壓應力條件下鐵鎵合金棒材的高頻磁特性，對現有的靜態J-A模型進行改進，建立了計及壓應力變化影響的高頻動態磁滯模型。主要結論如下：

1）本文在磁場頻率=1～9 kHz、磁場強度=1 000～6 000 A/m的條件下，測量了外施壓應力從0 MPa增加到60 MPa時，鐵鎵合金棒材的動態磁滯回線，可知隨著壓應力增加，回線縱向變窄，振幅磁導率、剩磁和磁能損耗逐漸減小。

2）從經典的靜態J-A模型出發，考慮高頻渦流損耗場和剩余損耗場的影響，引入分數階導數優化高頻渦流場表達式，構建高頻動態磁滯模型；采用擬合參數法計及壓應力的影響，基于混合粒子群算法對不同壓應力下的實驗數據進行參數辨識，按照模型參數的變化的規律，將J-A模型各個參數擬合為壓應力的多項式函數，建立了計及壓應力影響的變系數高頻磁滯模型。所建立的高頻動態磁滯模型在高頻磁場與應力場耦合的綜合工況下，計算結果與實測值吻合性較好。在高頻勵磁下，由于引入分數階導數對渦流場進行修正，使模型具有良好的頻率適應性，最大誤差量為6.88%，平均誤差量為4.71%；在不同磁場強度下，最大誤差量為6.99%，平均誤差量為4.28%；通過擬合參數法，提高了模型的應力跟蹤能力，在改變壓應力時，最大誤差量為5.86%，平均誤差量為3.29%。

本文的研究工作可利用有限的實驗數據，有效地預測鐵鎵合金棒材所受外界壓應力變化時的高頻磁特性變化，可為高頻大功率磁致伸縮換能器件工程中的優化設計及性能調控提供理論和數據支持。

[1] 翁玲, 梁淑智, 王博文, 等. 考慮預應力的雙勵磁線圈鐵鎵換能器輸出特性[J]. 電工技術學報, 2019, 34(23): 4859-4869. Weng Ling, Liang Shuzhi, Wang Bowen, et al. Output characteristics of double-excited coil Fe-Ga transducer considering pre-stress[J]. Transactions of China Electrotechnical Society, 2019, 34(23): 4859-4869.

[2] Cao Shuying, Yue Xiufeng, Zheng Jiaju, et al. Dynamic coupled model of vibration system with galfenol damper considering eddy currents and hysteresis[J]. IEEE Transactions on Magnetics, 2020, 56(1): 1-4.

[3] 段娜娜, 徐偉杰, 李永建, 等. 一種考慮溫度和壓力影響的磁滯模型及其實驗驗證[J]. 電工技術學報, 2019, 34(13): 2686-2692. Duan Nana, Xu Weijie, Li Yongjian, et al. A temperature and stress dependent hysteresis model with experiment validation[J]. Transactions of China Electrotechnical Society, 2019, 34(13): 2686-2692.

[4] 杜杲嫻, 楊鑫, 韋艷飛, 等. 稀土超磁致伸縮棒材特性測試平臺優化與實驗研究[J]. 電工技術學報, 2021, 36(18): 3867-3875. Du Gaoxian, Yang Xin, Wei Yanfei, et al. Optimization and experimental research on the test platform of rare-earth gaint magnetostrictive rod characteristics[J]. Transactions of China Electrotechnical Society, 2021, 36(18): 3867-3875.

[5] 趙志剛, 馬習紋, 姬俊安. 基于AFSA與PSO混合算法的J-A動態磁滯模型參數辨識及驗證[J]. 儀器儀表學報, 2020, 41(1): 26-34. Zhao Zhigang, Ma Xiwen, Ji Jun'an. Parameter identification and verification of J-A dynamic hysteresis model based on hybrid algorithms of AFSA and PSO[J]. Chinese Journal of Scientific Instrument, 2020, 41(1): 26-34.

[6] Hamada S, Louai F Z, Nait-Said N. Modeling and analysing the influence of both frequency and mechanical stress on ferromagnetic sheets NO Fe 3%Si using improved low frequency diffusion equation model[C]//2020 4th International Conference on Advanced Systems and Emergent Technologies (IC_ASET), Hammamet, Tunisia, 2020: 100-105.

[7] Messal O, Sixdenier F, Morel L, et al. Temperature dependent extension of the Jiles-Atherton model: study of the variation of microstructural hysteresis parameters[J]. IEEE Transactions on Magnetics, 2012, 48(10): 2567-2572.

[8] Jackiewicz D, Szewczyk R, Kachniarz M, et al. Modelling the influence of stresses on magnetic characteristics of the elements of the truss using extended Jiles-Atherton model[J]. Acta Physica Polonica A, 2017, 131(4): 1189-1191.

[9] Bernard L, Mailhé B J, ávila S L, et al. Magnetic hysteresis under compressive stress: a multiscale-Jiles-Atherton approach[J]. IEEE Transactions on Magnetics, 2020, 56(2): 1-4.

[10] 李長云, 劉亞魁. 直流偏磁條件下變壓器鐵心磁化特性的Jiles-Atherton修正模型[J]. 電工技術學報, 2017, 32(19): 193-201. Li Changyun, Liu Yakui. Modified Jiles-Atherton model of transformer iron core magnetization characteristics with DC bias[J]. Transactions of China Electrotechnical Society, 2017, 32(19): 193-201.

[11] 陳彬, 秦小彬, 唐波, 等. 基于R-L分數階導數的動態J-A磁滯模型及其特征參數辨識算法[J]. 中國電機工程學報, 2022, 42(12): 4590-4603. Chen Bin, Qin Xiaobin, Tang Bo, et al. Dynamic J-A hysteresis model based on R-L fractional derivative and its characteristic parameter identification algorithm[J]. Proceedings of the CSEE, 2022, 42(12): 4590-4603.

[12] Hussain S, Lowther D A. Prediction of iron losses using Jiles–Atherton model with interpolated parameters under the conditions of frequency and compressive stress[J]. IEEE Transactions on Magnetics, 2016, 52(3): 1-4.

[13] Malika Y, Sebti B, Adel B. A theoretical characterization of the coupling effects of frequency and mechanical stresses on the magnetic properties of the ferromagnetic material[C]//2018 International Conference on Communications and Electrical Engineering (ICCEE), El Oued, Algeria, 2019: 1-5.

[14] Zhang B, Gupta B, Ducharne B, et al. Dynamic magnetic scalar hysteresis lump model based on Jiles-Atherton quasi-static hysteresis model extended with dynamic fractional derivative contribution[J]. IEEE Transactions on Magnetics, 2018, 54(11): 1-5.

[15] 陳彬, 秦小彬, 萬妮娜, 等. 基于R-L型分數階導數與損耗統計理論的鐵磁材料高頻損耗計算方法[J]. 電工技術學報, 2022, 37(2): 299-310. Chen Bin, Qin Xiaobin, Wan Nina, et al. Calculation method of high-frequency loss of ferromagnetic materials based on R-L type fractional derivative and loss statistical theory[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 299-310.

[16] Ducharne B, Sebald G, Guyomar D, et al. Dynamics of magnetic field penetration into soft ferromagnets[J]. Journal of Applied Physics, 2015, 117(24): 243907.

[17] Zhao Hanyu, Ragusa C, Appino C, et al. Energy losses in soft magnetic materials under symmetric and asymmetric induction waveforms[J]. IEEE Transactions on Power Electronics, 2019, 34(3): 2655-2665.

[18] Zhao Hanyu, Ragusa C, de la Barrière O, et al. Magnetic loss versus frequency in non-oriented steel sheets and its prediction: minor loops, PWM, and the limits of the analytical approach[J]. IEEE Transactions on Magnetics, 2017, 53(11): 1-4.

[19] Liu Ren, Li Lin. Analytical prediction model of energy losses in soft magnetic materials over broadband frequency range[J]. IEEE Transactions on Power Electronics, 2021, 36(2): 2009-2017.

[20] 李曉萍, 彭青順, 李金保, 等. 變壓器鐵心磁滯模型參數辨識[J]. 電網技術, 2012, 36(2): 200-205. Li Xiaoping, Peng Qingshun, Li Jinbao, et al. Parameter identification of hysteresis loop model for transformer core[J]. Power System Technology, 2012, 36(2): 200-205.

[21] Rasilo P, Singh D, Aydin U, et al. Modeling of hysteresis losses in ferromagnetic laminations under mechanical stress[J]. IEEE Transactions on Magnetics, 2016, 52(3): 1-4.

[22] 王洋, 劉志珍. 基于蛙跳模糊算法的Jiles Atherton鐵心磁滯模型參數確定[J]. 電工技術學報, 2017, 32(4): 154-161. Wang Yang, Liu Zhizhen. Determination of Jiles Atherton core hysteresis model parameters based on fuzzy-shuffled frog leaping algorithm[J]. Transactions of China Electrotechnical Society, 2017, 32(4): 154-161.

Analysis and Modeling of High Frequency Magnetic Properties of Rod Gallium Iron Alloy under Variable Compressive Stress

Huang Wenmei1,2Tao Zheng1,2Guo Pingping1,2Zhang Weishuai1,2Weng Ling1,2

（1.State Key Laboratory of Reliability and Interlligence of Electrical Equipment Hebei University of Technology Tianjin 300130 China 2. Key Laboratory of Electromagnetic Field and Electrical Apparatus Reliability of Hebei Province Hebei University of Technology Tianjin 300130 China）

The output characteristics of high-frequency and high-power magnetostrictive transducer devices are closely related to the compressive stress. Applying a certain compressive stress can increase the magnetostrictive coefficient of the core component magnetostrictive rod and increase the output power of the device. But an inappropriate compressive stress can deteriorate the performance of the device. To investigate the stress sensitivity of magnetostrictive rods under high frequency excitation conditions In this paper, we built a high-frequency magnetic property test system for magnetostrictive materials, and measured the dynamic magnetic property curves of iron gallium alloy rod under different excitation conditions (variable compressive stress, variable excitation frequency and magnetic field strength ). Based on the measured hysteresis lines, it shows that when the frequency and applied magnetic field strength are certain, with the increase of compressive stress, the magnetic permeability of iron gallium alloy rod decreases and the magnetization process of the material becomes more and more difficult. However, the applied larger compressive stress can reduce the magnetic loss of iron gallium alloy rod with a certain magnetic field strength, while the remanent magnetization decreases and the hysteresis effect is weakened, which improves the real-time of the rod.

To address the problem that conventional hysteresis models cannot account for the effects of compressive stress. Based on the existing static J-A hysteresis model, a high-frequency dynamic hysteresis model is established by taking into account the eddy current loss and residual loss and using fractional order derivatives to modify the high-frequency eddy current field expressions. Then improved high-frequency dynamic hysteresis model related to external applied compressive stress by introducing compressive stress-related terms to modify model parameters.

Analysis of the experimental data and the model calculation results show that the model calculation results have good frequency adaptation at high frequencies due to the consideration of the dynamic loss field and the introduction of fractional order derivatives. Comparing the model calculation results with the measured hysteresis loop area at high frequency excitation of= 1～9 kHz, the maximum error amount is 6.88% and the average error amount is 4.71%. The model also reflects more accurately the change in the amount of loss when the magnitude of magnetic field strength is changed, with a maximum error of 6.99% and an average error of 4.28% under different magnetic field strengths (=1 000～6 000 A/m). Due to the use of J-A model parameters with compressive stress correlation term, the model can effectively take into account the influence of compressive stress on the calculation results, and the calculation results have high accuracy under the conditions of variable external applied compressive stress (=0～60 MPa). The maximum error of hysteresis loop area is 5.86% and the average error is 3.29%. The model can use limited experimental data to effectively predict the variation of the high frequency magnetic properties of iron gallium alloy rod under variable compressive stress conditions. It provides theoretical and data support for the optimal design and performance regulation in the engineering of high-frequency high-power magnetostrictive transducer devices.

Rod gallium iron alloy, compressive stress, high frequency magnetic properties, improved hysteresis model

國家自然科學基金資助項目（51777053, 52077052, 52130710）。

2022-05-13

2022-06-24

10.19595/j.cnki.1000-6753.tces.220819

TM274

黃文美 女，1969年生，博士，教授，研究方向為磁性材料與器件、電機電器及其控制。E-mail：huzwm@hebut.edu.cn（通信作者）

陶 錚 男，1996年生，碩士研究生，研究方向為磁性材料與器件、電機電器及其控制。E-mail：961851321@qq.com

（編輯 李 冰）