一種有效且穩健的變量選擇方法

胡毓榆 郭子君 陳夢醒 樊亞莉

摘要： 當數據中存在異常值時，一些基于最小二乘估計的統計模型會產生較大的偏差，最小一乘 估計對異常值具有比較強的抵抗能力。考慮到數據中可能存在異常值的情況，用絕對值損失代替 平方損失，針對同時具有變量稀疏性和相鄰系數差分稀疏性這種結構的線性模型，提出了最小一 乘融合熔斷自適應嶺估計模型（LAD-Fused-BAR）。該模型將上一步估計的回歸系數倒數的平方作 為下一步懲罰權重， 自適應地給予不同變量不同的懲罰， 通過不斷迭代得到最終解。運用交替方向 乘子法（ADMM）求解 LAD-Fused-BAR模型，并證明了 ADMM算法的收斂性。數值模擬和實證 分析也驗證了該模型的有效性和穩健性。

關鍵詞： LAD-Fused-BAR 模型；穩健回歸； 交替方向乘子法

中圖分類號：? O 212.1???????????? 文獻標志碼：?? A

An effective and robust variable selection method

HU Yuyu， GUO Zijun， CHEN Mengxing， FANYali

（College of Science， University of Shanghai for Science and Technology， Shanghai 200093， China）

Abstract： Some statistical models based on least squares estimation will produce large bias when there are outliers in the data. The least absolute deviation has strong resistance to outliers. Considering the influence of the outliers in the data， the square loss was replaced with the absolute loss. Aiming at the linear model of a structure that has both variable sparsity and sparsity of adjacent coefficient differences， the least absolute deviation? fused broken? adaptive ridge? estimation model（ LAD-Fused-BAR）was proposed. The square of the reciprocal of the regression coefficient estimated in the previous step was taken as the penalty weight for the next step， different penalties were adaptively given to different variables， and the final solution was obtained through continuous iteration. The alternating direction multiplier? method （ ADMM）was? adopted? to?? solve? the? LAD-Fused-BAR? model?? and? prove? the convergence? of? the? ADMM? algorithm.? Additionally，? numerical? simulation? and? empirical? analysis confirm the efficacy and robustness of the proposed methodology.

Keywords： LAD-Fused-BAR ; robust regression; ADMM

大數據時代的生活中到處充滿著海量的數據[1]，通過分析這些數據，研究者可以探究出潛在的商業信息及其應用價值。然而，隨著科技的發展，數據中變量的維度呈指數級增長，并且數據中經常夾雜著噪聲和冗余信息。另外，這些變量中往往存在一些不相關變量和冗余變量，給數據分析帶來了困難，影響估計的效率以及精度。為了解決這個問題，通常利用變量選擇將重要的變量篩選出來，從而達到降維的目的。

1 文獻綜述

關于變量選擇問題，很多研究者從統計學角度作了大量研究。1973年，Akaike 等[2]提出了 AIC 準則。1978年， Schwarz[3]在貝葉斯的框架下提出了 BIC 準則。然而，當變量的維度增加時，這種基于 AIC 和 BIC 準則選取最優變量子集的傳統方法計算效率較低。近十幾年來，通過在損失函數后面加入一個懲罰函數的方法使得變量選擇有了較大的發展，并且這種加入懲罰函數的方法可以同時實現參數估計以及變量選擇的目的。1995年， Natarajan[4]提出了在損失函數后面加入 l0范數，通過懲罰非零元素個數從而達到變量選擇的目的。這個懲罰函數是一種很直觀的形式，但是l0范數是非凸且不連續的函數，這就導致了最小化l0問題是一個 NP-Hard 問題。1996年，Tibshirani[5]提出了 LASSO（least absolute shrinkage and selection operator）懲罰，通過加入l1范數從而得到一個稀疏解。l1范數是l0范數的一個凸松弛。盡管l1范數是一個凸函數且易于求解，但是 LASSO 估計的參數是有偏的[6]。為了解決這個問題，近些年有許多學者提出了非凸的懲罰函數來解決估計的有偏問題。2001年， Fan 等[6]提出了 SCAD（smoothly clippedabsolute deviation）懲罰。2006年， Zou[7]在 LASSO 的基礎上提出了 Adaptive LASSO 懲罰，該方法是對 LASSO 的一種改進。 SCAD 和 Adaptive LASSO 在一定條件下都滿足 Oracle性質。2008年，Candès 等[8]提出了對數懲罰。2010年，Zhang[9]提出了 MCP （minimax concave penalty）懲罰。很多研究結果表明非凸懲罰函數在理論分析以及實際應用中具有更優秀的表現[10]。

然而，對于一些具有一定結構的復雜數據，例如信號處理、基因表達等分段常數函數類型的數據，上述方法并不適用。2005年，Tibshirani 等[11] 在 LASSO 方法的基礎上提出了 Fused-LASSO 方法，在考慮變量稀疏性的同時還考慮了變量差分的稀疏性。這種方法能夠同時解決變量稀疏性和獲取噪聲信號或者基因序列中非零片段的情況。2011年， Tibshirani 等[12]提出了（2D）Fused-LASSO 方法，該方法能夠處理圖像去噪的問題。

2017年， Dai 等[13]提出了一種熔斷自適應嶺估計（BAR）方法，該方法本質上是一種迭代重加權嶺估計方法，它能夠很有效地同時進行變量選擇和參數估計。相比于之前文獻提到的方法，BAR 方法的優點是參數估計通過迭代的方式進行，在每一步迭代過程中上一步參數的估計值將作為下一步估計的權重。因此， BAR 方法中的權重是自適應更新的，并且加入的懲罰是l2懲罰，目標函數是嚴格凸以及可微的。因此，每一步迭代過程都可以求得顯式解，最后通過不斷迭代得到最終的估計。 Dai 等[13]證明了他們提出的估計具有 Oracle 性質和 Group Effect，并且 Dai 在最后數值實驗中表明了 BAR 方法比上文所述幾種方法更有效。

2020年， Dai 等[14]將 BAR 推廣為廣義的形式，這種廣義的形式能夠估計出回歸系數的任意結構，例如稀疏結構、分段常數結構以及線性趨勢結構。融合熔斷自適應嶺估計（Fused-BAR）是廣義 BAR 方法的一種特殊形式，它能夠很有效地進行變量選擇以及識別出噪聲信號或者基因序列中非零片段的情況。文獻[14]證明了在一定條件下，在 BAR 方法迭代過程中，估計值會收斂到一個不動點。如果事先給出一個正確的初始值，那么最終 BAR 方法估計的效果就很好。文獻[14]在數值實驗中證實了 Fused-BAR 方法比 Fused-LASSO 方法更有效。

然而 BAR 方法采用的損失是平方損失，平方損失對于異常值和重尾數據比較敏感。當數據中存在異常值時，估計的參數會產生較大的偏差和方差，通常采用穩健的損失函數作為代替。例如 Huber 損失、 t 型損失[15]、穩健的估計方程[16]、絕對值損失[17]。這些損失函數對異常值和重尾數據具有一定的抵抗能力。2007年， Wang 等[17]在 LASSO 方法的基礎上，將平方損失替換為絕對值損失，提出了 LAD-LASSO 方法，與 LASSO 方法相比， LAD-LASSO 方法也可以同時進行變量選擇和參數估計，并且對于重尾分布的數據和帶有異常值的數據有抵抗力。2016年，張環[18]在 Fused- LASSO 方法的基礎上用絕對值損失代替平方損失，提出了 LAD-Fused-LASSO 方法，既能有效地將相鄰特征選出來，又能抵抗異常值。

基于以上文獻的啟發，本文在 Fused-BAR 方法的基礎上提出了一種穩健且有效的變量選擇模型，稱為最小一乘融合熔斷自適應嶺估計（LAD- Fused-BAR）。它是將 Fused-BAR 估計方法中的平方損失替換成絕對值損失，從而實現穩健且有效的變量選擇。 Fused-BAR 在迭代過程中每一步可以求出顯式解，然而把平方損失替換成絕對值損失之后，由于多了一項非光滑項，要優化的目標函數無法求顯示解，并且基于梯度的一些方法也失效了，這給計算帶來了很大的挑戰。在處理非光滑函數l1上，文獻[19]中提出了最小角回歸，文獻 [20]提出了內點法。然而，這些算法的計算復雜度較大，在大規模數據上表現不佳。2010年， Boyd 等[21]首次提出了交替方向乘子法（ADMM）。 Glowinski 等[22]受到啟發，將 ADMM 方法應用到 LASSO 以及 Group-LASSO 上。因此，本文采取交替方向乘子法（ADMM）進行求解，并證明了 ADMM 算法的收斂性。

2 最小一乘融合熔斷自適應嶺估計（LAD-Fused-BAR）

考慮一般的線性回歸模型

式中： Y =（y1··· yn），是響應變量；β∈ Rp，是回歸系數； X =（x1··· xn）T ，是協變量；ε=（ε1···εn），εi的均值為0，方差為σ2，ε的各分量相互獨立。

Dai 在文獻[14]中提出的 Fused-BAR 估計方法如下所示：

式中： g ）表示估計的參數；λ1和λ2是調節參數。

若在式（2）中只考慮λ1對應的懲罰項，這就是文獻[13]提出的 BAR 方法。式（2）所定義的g ）是在上一步的估計β（?）基礎上的更新公式。可以看到在更新公式中，不僅對變量施加懲罰，也對相鄰變量的差分進行懲罰。BAR 估計和文獻[7]中提出的 Adaptive LASSO 方法在思想上類似，對于估計值比較大的變量給它較小的懲罰，而對于估計值比較小的變量給它較大的懲罰。但是 Adaptive LASSO 的權重并不是根據上次估計自適應的，而是事先估計的一個常數。文獻[14]認為，在每次迭代過程中，將上一次估計的{gk（β）}?2作為權重比用常數作為權重更好。隨著迭代的不斷進行，對于真實β中為零的變量的權重會趨于無窮，而對于真實β中非零變量的權重會趨于一個常數。由于 BAR 方法使用的懲罰是l2懲罰，因此，每一步迭代都能產生顯式解。

文獻[14]中將嶺估計

作為初始值，式中，ξ>0是一個正數，I 是單位矩陣。因此，上述提出的估計即為融合熔斷自適應嶺估計（Fused-BAR），最終估計可以通過迭代算法βj = g{βj?1}的極限求出來，即

定義

是一個（p?1）× p的矩陣，則式（2）可以寫成

其中

如果要解決的是信號處理、基因檢測以及圖像去噪等問題，只要令X = I即可。式（4）中目標函數用的是平方損失，當響應變量中存在異常值時，該損失函數會放大異常值的影響。受到文獻[17-18]的啟發，本文用絕對值損失代替平方損失，得到最小一乘融合熔斷自適應嶺估計模型

3 算法求解

由于本文的方法是將文獻[14]中的平方損失替換成了絕對值損失，在目標函數中多了一項非光滑項，使得在每一次迭代過程中無法求出顯式解。當數據規模很大時，最小角回歸以及內點法計算復雜度高。Boyd 等[21]在2010年提出了 ADMM 算法，通過選取一個光滑函數來逼近模型的非光滑項，并且 ADMM 方法在大規模數據上計算效率高。除此之外， ADMM 算法在處理該問題時，使得每一步迭代都有顯式解，這充分地保障了 ADMM 求解 LAD-Fused-BAR 問題的有效性。

為了應用交替方向乘子方法，引入輔助變量τ ，則式（6）等價于

式（7）的增廣拉格朗日形式為

β的更新為

令式（9）右端微分為0得到

τ的更新為

該優化問題可以用軟閾值算法進行求解得到，即

α的更新為

運用算法 ADMM 求解本文 LAD-Fused- BAR 模型的具體流程如下：

4 收斂性證明

文獻[23]已經給出了關于 ADMM 收斂性的一個框架。為了建立 ADMM 算法的收斂性，以算法的第 k+1次迭代值作為一個變分 VI 問題[23]，可以得到下面引理。其中， k 表示迭代次數。下面4個引理在文獻[23]中已經得到證明，本文不再贅述。

引理1 令{wk }={βk ;τk ;αk }表示由算法產生的序列，{υk }={τk ;αk }，有{wk}={βk ;τk ;αk}（υk+1一υ*）TH （υk 一υk+1）>（wk+1一w*）Tη（τk ;τk+1）

其中

引理2

引理3

引理4

定理1

證明

由單調有界定理得到，{υk }收斂至υ∞=（τ∞;α∞），根據式（10）得到β0收斂至β∞ ，證畢。

5 數值模擬

真實的β?如下所示生成：

其中，非零系數的個數為10， n =200; p =100; xij? N（0;1）;1< i < n ，1< j < p 。εi服從均值為0，標準差為0.01的正態分布， y由式（1）生成。為了研究穩健性，選取c%的數據進行污染，通過將 c%的εi換成服從均值為30、標準差為0.1的正態分布的噪聲值，下文分別以 c=0，5，10進行模擬。

在 Fused-BAR 程序中，對ξ ， λ1，λ2這3個參 數進行調節。參數選擇和文獻[14]一樣，ξ的選擇用5折交叉驗證的方法。對于λ1，λ2的選擇，用網格搜索的方法進行篩選，將λ1和λ2取[0.0001，0.001，0.01， 0.1，1，10]，然后通過5折交叉驗證來選取最優參數。LAD-Fused-BAR 方法里面有4個超參數：ξ ， λ1，λ2，u，初始值β（?）R 的選取和 Fused-BAR 采取相同的方式。若同時遍歷余下的3個超參數，計算時間較慢。因此，采取先固定u然后利用5折交叉驗證的方法選取最優的λ1和λ2，然后再固定λ1和λ2來選取最優的u。

關于指標選取，既要考慮估計的偏差又要考慮變量選擇的準確率。因此采用平均絕對誤差來表示估計的偏差，即

式中， wMAE為平均絕對誤差。

假設θTP為正確估計為非零的個數，θFP 為錯誤估計為非零的個數，θFT為正確估計為零的個數，θFN為錯誤估計為零的個數，則可以用準確率θACC =θTP +θT（θT）N（P）θF（θT）P（N）+θFN 、精確率θPRE =θTPθ PθFP 、召回率θREC =θTPθ PθFN 、 F1=2θTP θ（θ）FP（TP）+θFN 指標來判別變量選擇的能力。將數據劃分成50份，其中一份作為測試集，余下部分作為訓練集。運行50次后分別求出平均值如表1所示。

從表1可以看出，在沒有污染的情況下，LAD-Fused-BAR 和 Fused-BAR 估計的準確率都為1，兩種方法都能全部準確地估計出真實的β*。雖然 Fused-BAR 估計的偏差會比 LAD-Fused-BAR 更小，但差距并不是很大，這證明了 LAD-Fused- BAR 在無污染情況下估計的有效性。然而，在有污染的情況下， LAD-Fused-BAR 的平均絕對誤差比 Fused-BAR 小，并且其他指標都比 Fused-BAR 要大。這說明 LAD-Fused-BAR 在當數據有異常值的時候表現更穩健，估計準確率和精度都要比Fused-BAR 更優秀。進一步，用不同污染情況下的系數分布來直觀地表示兩種方法變量選擇的能力，如圖1～3所示。

圖1也說明了在無污染的情況下， Fused-BAR 和 LAD-Fused-BAR 都能將β*估計出來，但是當數據有污染時， Fused-BAR 的估計值出現偏差，不能將真實的β*準確估計出來，而 LAD-Fused-BAR 方法依然能將真實的β*估計出來，說明在數據有異常值的情況下， LAD-Fused-BAR 方法更穩健。

6 實證分析

在癌癥研究中，拷貝數變異數據（CNV）是一個很重要的數據集，該數據集具有相鄰關系。也就是說， CNV 通常是各種長度的線段的形式[24]。比較基因組雜交（CGH）陣列是掃描基因組中 CNV 的一個很有效的工具。可以通過 CGH 掃描 CNV 來檢測基因是否發生改變，即 DNA 拷貝數的缺失和增加。為了更方便地檢測基因是否改變，通常將 CGH 數據陣列設置為腫瘤細胞中的 DNA 拷貝數與正常或參考細胞中的 DNA 拷貝數的 log 2比率。因此，當 CGH 為正值時表示 DNA 拷貝數增加，而當其為負值時，表示 DNA 拷貝數缺失。CGH 通常由具有零值分段區域的分段常數序列或函數逼近。

近年來，有許多方法已經對 CGH 數據進行研究。例如 EM 算法[25]、隱馬爾可夫方法[26]、 Fused- LASSO[27]以及 Fused-BAR[14]。這些方法可以用于 CGH 的可視化以及用于 CGH 分段值的推斷。本文分別采用Fused-BAR 和LAD-Fused-BAR 來分析CGH 數據， CGH 數據的獲得來自于 R 包 cghFlasso。為了驗證穩健性，將d*的數據進行污染，通過將d*的數據加上5。在本文中 d 分別取0，3，5進行實驗。

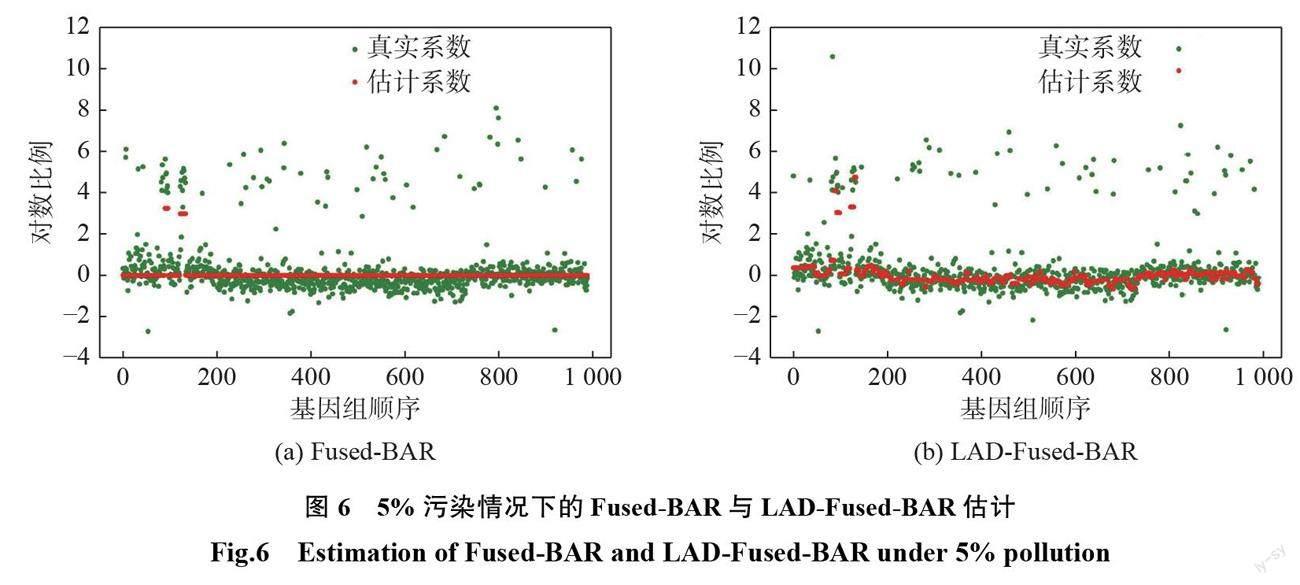
參數選擇和模擬時一樣采取網格搜索的方式，該實驗解決了一個信號去噪的問題。因此，將數據的奇數行作為訓練集，偶數行作為驗證集，用兩折交叉驗證選取最優參數。實驗結果如表2和圖4～6所示。

由表2可見，當數據不加污染時，雖然 Fused- BAR 方法估計的 MAE 比 LAD-Fused-BAR 方法的要小，但差別不大，說明在無污染的情況下，LAD- Fused-BAR 估計是有效的。但是當數據有一部分被污染時， LAD-Fused-BAR 方法估計的 MAE 要比 Fused-BAR 更小，說明 LAD-Fused-BAR 在數據有污染時更穩健。從圖4可以看出，在無污染的情況下， Fused-BAR 方法能夠將 CGH 非零片段識別出來， LAD-Fused-BAR 方法也能將非零片段識別出來。而 LAD-Fused-BAR 識別出來的不像 Fused-BAR 是一條直線，這是因為本文算法求的是近似解，因此，在噪聲比較大的情況下估計的信號會有波動。但是，當數據被污染時，LAD-Fused- BAR 估計的 MAE 比 Fused-BAR 方法的要小，說 明在有污染的情況下，LAD-Fused-BAR 方法更穩健。

從圖5和圖6可以看出，相比于圖4，盡管 BAR 方法能夠估計出一條直線，但是在有污染的情況下 Fused-BAR 方法估計的系數絕大部分都被壓縮到0，體現不出分段常數的形式。這說明 Fused-BAR 估計在有異常值的情況下不穩健。由于本文方法求的是近似解而不是解析解，所以當噪聲比較大時，不能估計出一條分段直線的形式。但是， LAD-Fused-BAR 方法還是能夠判斷出估計的信號是呈分段常數的形式，這說明 LAD-Fused- BAR 在數據中有異常值的情況下更穩健。

7 總結和展望

在 Fused-BAR 變量選擇的框架下提出了一種穩健且有效的變量選擇方法，通過把平方損失替換成絕對值損失從而達到穩健的效果。然而，將平方損失替換成絕對值損失后，導致要優化的目標函數無法求出顯式解。因此，采用 ADMM 進行求解，并且證明了 ADMM 算法的收斂性。模擬結果以及實證分析顯示，與 Fused-BAR 方法相比， LAD-Fused-BAR 方法在數據有異常值的情況下更穩健。在面對噪聲比信號大的情況時，本文提出的算法由于得到的是近似解，偏差較大，后續可以考慮改進算法和其他穩健的損失函數。

參考文獻：

[1] CHEN C L P， ZHANG C Y. Data-intensive applications， challenges， techniques and technologies： a survey on BigData[J]. Information Sciences， 2014， 275：314–347.

[2] AKAIKE H. Information theory and an extension of themaximum likelihood principle[M]//PETROV B N， CSAKI F. Proceedings of the 2nd International Symposium on Information Theory. Budapest： Akademiai Kiado， 1973：267–281.

[3] SCHWARZ G. Estimating the dimension of a model[J]. The Annals of Statistics， 1978， 6（2）：461–464.

[4] NATARAJAN B K. Sparse approximate solutions to linear systems[J]. SIAM Journal on Computing， 1995， 24（2）：227–234.

[5] TIBSHIRANI R. Regression shrinkage and selection via the lasso[J]. Journal of the Royal Statistical Society：Series B （Methodological）， 1996， 58（1）：267–288.

[6] FAN J Q， LI R Z. Variable selection via nonconcave penalized likelihood and its oracle properties[J]. Journal of the American Statistical Association， 2001， 96（456）：1348–1360.

[7] ZOU H. The adaptive lasso and its oracle properties[J]. Journal of the American Statistical Association， 2006， 101（476）：1418–1429.

[8] CANDèS E J， WAKIN M B， BOYD S P. Enhancing sparsity by reweighted ?1 minimization[J]. Journal of Fourier Analysis and Applications， 2008， 14（5）：877–905.

[9] ZHANG C H. Nearly unbiased variable selection under minimax concave penalty[J]. The Annals of Statistics， 2010， 38（2）：894–942.

[10] XU Z B. Data modeling： visual psychology approach and L1/2? regularization? theory[C]//Proceedings? of? the International Congress of Mathematicians 2010 （ICM 2010）. Hyderabad： World Scientific， 2010：3151–3184.

[11] TIBSHIRANI R， SAUNDERS M， ROSSET S， et al. Sparsity and smoothness via the fused lasso[J]. Journal of the Royal Statistical Society： Series B （Statistical Methodology）， 2005， 67（1）：91–108.

[12] TIBSHIRANI R J， TAYLOR J. The solution path of the generalized lasso[J]. The Annals of Statistics， 2011， 39（3）：1335–1371.

[13] DAI L L， CHEN K N， SUN Z H， et al. Broken adaptive ridge regression and its asymptotic properties[J]. Journal of Multivariate Analysis， 2018， 168：334–351.

[14] DAI L L， CHEN K N， LI G. The broken adaptive ridge procedure and its applications[J]. Statistica Sinica， 2020， 30（2）：1069–1094.

[15]鐘先樂， 樊亞莉， 張探探.基于 t 函數的穩健變量選擇方法[J].上海理工大學學報， 2017， 39（6）：542–548.

[16] FAN Y L， QIN G Y， ZHU Z Y. Variable selection in robust regression models for longitudinal data[J]. Journal of Multivariate Analysis， 2012， 109：156–167.

[17] WANG H S， LI G D， JIANG G H. Robust regression shrinkage and consistent variable selection through the LAD-Lasso[J]. Journal of Business & Economic Statistics， 2007， 25（3）：347–355.

[18]張環. Fused-LASSO 懲罰最小一乘回歸的統計分析與優化算法[D].北京：北京交通大學， 2016.

[19] EFRON B， HASTIE T， JOHNSTONE I， et al. Least angle regression[J]. The Annals of Statistics， 2004， 32（2）：407–499.

[20] KIM S J， KOH K， LUSTIG M， et al. An interior-point method for large-scale ?1-regularized least squares[J]. IEEE Journal of Selected Topics in Signal Processing， 2007， 1（4）：606–617.

[21] BOYD S， PARIKH N， CHU E， et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and Trends in Machine Learning， 2011， 3（1）：1–122.

[22] GLOWINSKI R， MARROCO A. Sur l'approximation， paréléments finis d'ordre un， et larésolution， par pénalisation- dualité d'une classe de problèmes de Dirichlet non linéaires[J]. Revue Fran? aised'automatique， Informatique， et Recherche Opérationnelle. Analyse Numérique， 1975， 9（R2）：41–76.

[23]何炳生.凸優化和單調變分不等式收縮算法的統一框架[J].中國科學：數學， 2018， 48（2）：255–272.

[24] RIPPE R C A， MEULMAN J J， EILERS P H C. Visualization of genomic changes by segmented smoothing using an L0 penalty[J]. PLoS One， 2012， 7（6）： e38230.

[25] MYERS C L， DUNHAM M J， KUNG S Y， et al. Accurate detection of aneuploidies in array CGH and gene expression microarray data[J]. Bioinformatics， 2004， 20（18）：3533–3543.

[26] FRIDLYAND J， SNIJDERS A M， PINKEL D， et al. Hidden Markov models approach to the analysis of array CGH data[J]. Journal of Multivariate Analysis， 2004， 90（1）：132–153.

[27] TIBSHIRANI R， WANG P. Spatial smoothing and hot spot detection for CGH data using the fused lasso[J]. Biostatistics， 2008， 9（1）：18–29.

（編輯：丁紅藝）