灌區用水優化模型參數全局敏感性分析與不確定性優化

姜 瑤 顏澤文 黎良輝 閆 峰 熊呂陽

(1.南昌大學工程建設學院, 南昌 330031; 2.南昌大學鄱陽湖環境與資源利用教育部重點實驗室, 南昌 330031)

0 引言

灌溉是保障糧食生產的關鍵,尤其在干旱地區。在水資源短缺背景下,確保合理配置灌區水資源,提高農業用水效率具有十分重要的意義[1]。灌區水資源優化配置是實現灌區高效用水的有效手段之一。隨著相關研究的發展,灌區水資源優化配置逐漸由單一目標向多目標發展,由小尺度向大尺度過度,由傳統優化算法[2-4]向智能優化算法[5-7]發展,由確定性優化向不確定性優化發展[8-9]。優化模型的復雜性隨之增加,所涉及不確定性參數眾多,從而影響了此類模型的計算效率和實用性。

模型參數敏感性分析是一種研究模型輸入因素對輸出變量影響程度的方法,能很好地識別影響模型性能的關鍵參數,在模型參數率定、參數相關性和不確定性量化等方面都發揮重要作用[10]。模型參數敏感性分析通常分為局部敏感性分析和全局敏感性分析[11]。局部敏感性分析相對簡單,只檢測單個參數的改變對模型的影響,但其忽略了其他因素交互作用對模型結果的間接影響,因此該方法存在一定局限性[12]。全局敏感性分析能夠同時考慮多個參數變化以及參數間交互作用對模型結果的影響,更適用于具有復雜非線性特征的灌區優化問題,相關方法包括Morris篩選法[13]、EFAST(Extended Fourier amplitude sensitivity test)方法[14]、Sobol方法[15]、LH-OAT(Latin hypercube-One factor at a time)方法[16]和GLUE(Generalized likelihood uncertainty estimation)方法[17]等。參數敏感性分析方法在水文模型模擬研究中已得到廣泛應用[18-19],同時在泵站系統優化中也有部分應用[20-21],但在灌區水資源優化配置研究中的應用尚不多見。灌區水資源優化配置模型涉及的參數眾多,而且由于環境、地物類型、管理等因素變化的影響導致大多數參數具有不確定性。當前研究多是直接選擇某些不確定性參數并對其進行定量表征,缺少對模型參數的敏感性分析,這一方面可能忽略某些敏感性因素的影響,另一方面,過多不確定性參數的定量表征會使得模型結構復雜,增加求解過程的難度,降低模型計算效率和應用效果。因此,將敏感性分析方法應用到灌區水資源優化配置中,篩選出高敏感性的關鍵參數,以此進行不確定性下的灌區用水優化具有重要意義和實用價值。

本文將LH-OAT方法與灌區用水優化模型耦合,建立針對優化模型參數的全局敏感性分析方法,并以黑河流域中游盈科灌區為案例研究區,定量分析模型中不確定性參數的敏感性,篩選出高敏感性參數,以此進行不確定性下的灌區用水優化,獲得研究區考慮不確定性的灌溉用水配置方案。通過優化模型參數的全局敏感性分析,綜合考慮高敏感性參數及其不確定性對優化結果的影響,從而降低模型的復雜性,提高模型效率和實用性,為不確定性下的灌區水資源優化配置提供方法參考。

1 研究方法

1.1 LH-OAT方法

隨機OAT(One factor at a time)方法是MORRIS[13]在Monte Carlo的基礎上提出的。該方法原理為:若有M個參數,每次對一個參數進行隨機微小擾動,其他參數不變,共進行M次擾動,模型運行M+1次,即可得到M個參數各自的敏感度。然而,由于Monte Carlo方法隨機抽樣,產生大量樣本導致OAT方法的運算量變大。

針對Monte Carlo會產生大量樣本的問題,MCKAY等[22]在其基礎上提出了拉丁超立方(Latin hypercube,LH)抽樣法。該方法將整個參數空間等分成N層,對每個參數抽樣N次,并保證參數在每一等分層中抽樣1次,隨機組成N個LH參數組。LH抽樣法減少了樣本數量,確保了敏感性分析的高效性,但仍存在一些缺點,即當所有參數都變化時,并不能明確是哪一參數輸入值的變化引起的輸出結果的變化。

LH-OAT敏感性分析法將LH抽樣法和OAT敏感度分析方法相結合,克服了LH抽樣法和OAT方法的不足,減少了模型運行的次數和時間,也提高了準確性,有效地反映出模型輸出結果隨模型參數的微小改變而變化的敏感性程度。假設有M個參數,首先將這些參數空間等分成N層,然后在每一層中抽樣1次即1個LH抽樣點(包含M個參數的集合),共生成N個LH抽樣點。然后對每個LH抽樣點中的參數采用OAT方法擾動,即每次隨機改變1個參數,共有M次擾動。因此,1個LH抽樣點可生成M+1個參數組,N個LH抽樣點生成N×(M+1)個參數組。將模型運行N×(M+1)次,得到各參數的N次敏感度,將其取算術平均值后即可得到全局敏感度,其原理公式為

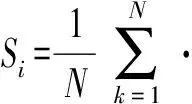
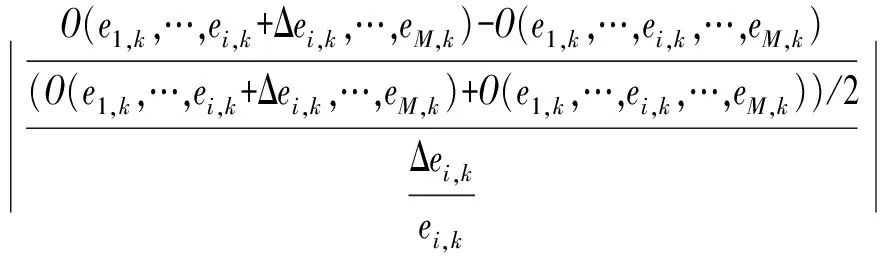
(1)

式中O——輸出變量

ei,k——第i個參數在第k個LH抽樣層中的取值

Δei,k——參數ei,k的某次擾動

Si——參數i的全局敏感度

1.2 優化模型

本文中的灌區用水優化模型在JIANG等[23]構建的區域灌溉用水優化模型基礎上改進得到。該優化模型具有2層結構,第1層為非線性規劃模型,以求解各子系統內灌溉用水和種植面積在不同作物-土壤單元間的最優分配問題;第2層采用動態規劃方法來優化灌溉用水在不同子系統之間的分配。有關模型的結構與數學表達詳見文獻[23]。本文在原模型基礎上,參考JIANG等[24]提出的方法,進一步對其結構進行了改進以提高模型效率,主要包括:①第1層所采用的各作物-土壤單元的作物水分生產函數(Crop water production function,CWPF)利用農業水文模型(SWAP-EPIC)與優化算法耦合的模擬-優化模型得到,相較于原模型中的現狀CWPF,其代表了各作物-土壤單元內的最優CWPF。②第2層采用基于各單元最優CWPF優化得到的各子系統用水-灌溉效益最優響應函數。有關該模擬-優化方法詳見文獻[24]。給定灌區總灌溉水量,模型從第2層開始依次求解,最終可得到各層最優結果。

1.3 方法構建

將LH-OAT方法與灌區用水優化模型耦合,對優化模型中的不確定性參數進行全局敏感性分析。耦合基于Matlab程序實現,具體步驟包括:①基于所構建灌區用水優化模型,選擇模型中的M個不確定性參數,并分別確定其取值空間。②采用LH抽樣法對選取的M個參數在值域內進行采樣,共生成N組抽樣點(每組包含M個參數)。③采用OAT方法逐一對每組抽樣點中的參數進行擾動,生成N×(M+1)個參數組。④以各參數組作為優化模型輸入,以優化模型的不同優化結果作為輸出變量,重復運行優化模型N×(M+1)次。⑤按式(1)計算各參數針對不同輸出變量的全局敏感度并排序,同時統計同一參數考慮所有輸出變量的敏感度全局排序。⑥根據敏感度全局排序,選擇高敏感性參數并將其在合理范圍內進行隨機采樣和組合,以此作為優化模型的不確定性輸入參數,重復運行優化模型,最終得到灌區用水的不確定性優化結果(圖1)。

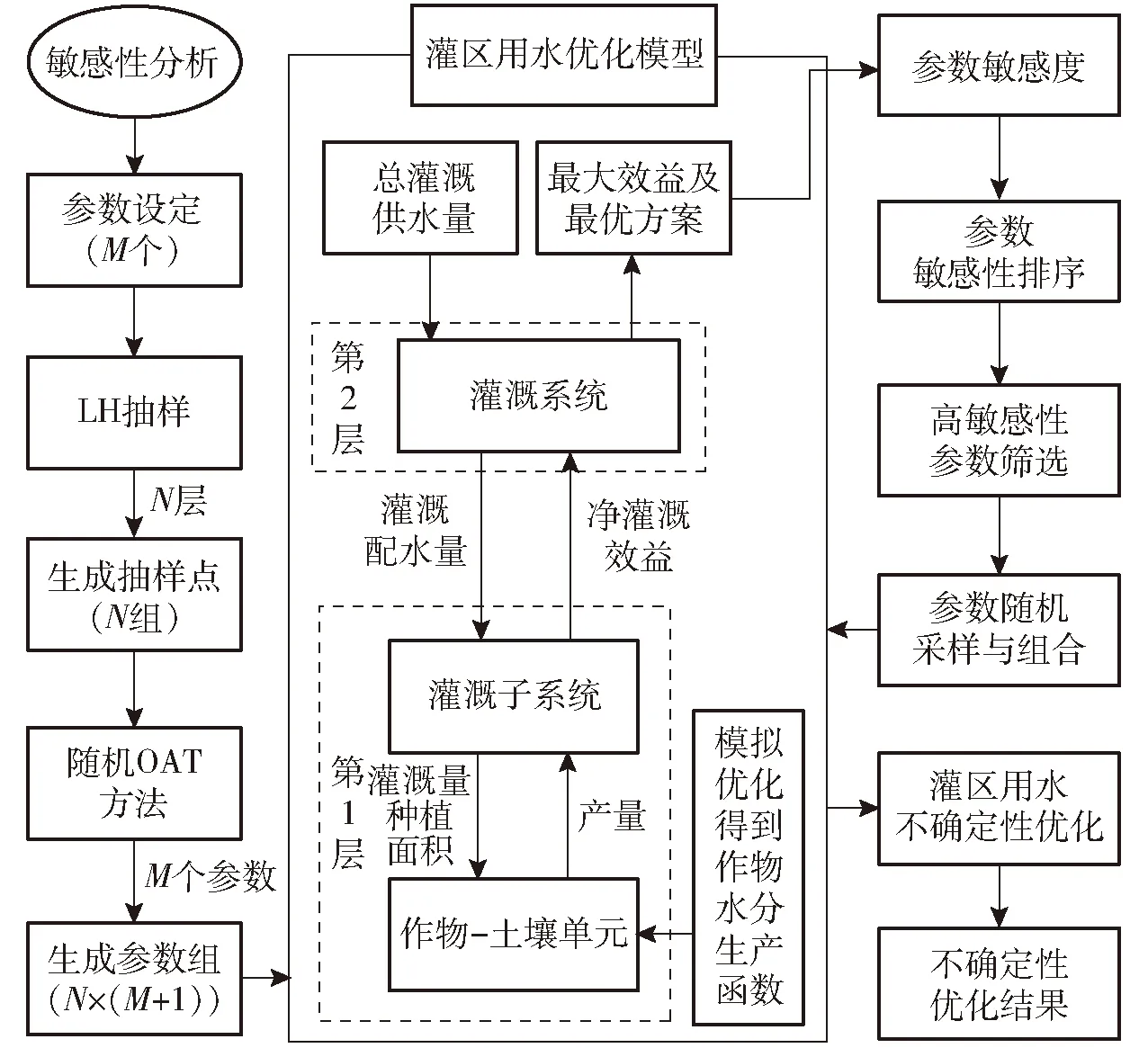
圖1 LH-OAT方法與灌區用水優化模型耦合示意圖

2 案例分析

2.1 研究區概況

以我國西北內陸黑河流域中游盈科灌區作為案例研究區(圖2)。盈科灌區為黑河流域中游綠洲的三大灌區之一,位于甘肅省張掖市,總面積192 km2,其中灌溉面積約131 km2,占總面積的68%。盈科灌區屬溫帶大陸性干旱氣候,冬夏較長且冬季寒冷干燥,春秋較短且多風少雨。灌區年平均氣溫 6.5～8.5℃,日照時數達3 000 h以上,多年平均降雨量僅為133 mm,無霜期140 d左右。灌區耕作層(0～140 cm)土壤質地主要以粉壤土和壤土為主,灌區上游(西南部)的耕作層底部也常出現砂礫石層[25]。灌區內主要種植玉米、春小麥和一些經濟作物,其中糧食作物種植面積約占總種植面積的83%,經濟作物以蔬菜為主,包括包菜、辣椒等,面積占15%左右[26]。盈科灌區灌溉渠系由1條主干渠、2條分干渠以及1 000多條下級分配渠道組成,由盈科干渠從東總干渠引黑河水進行灌溉,灌溉方式以漫灌或傳統畦灌為主。盈科灌區渠系及作物土壤分布見圖2。

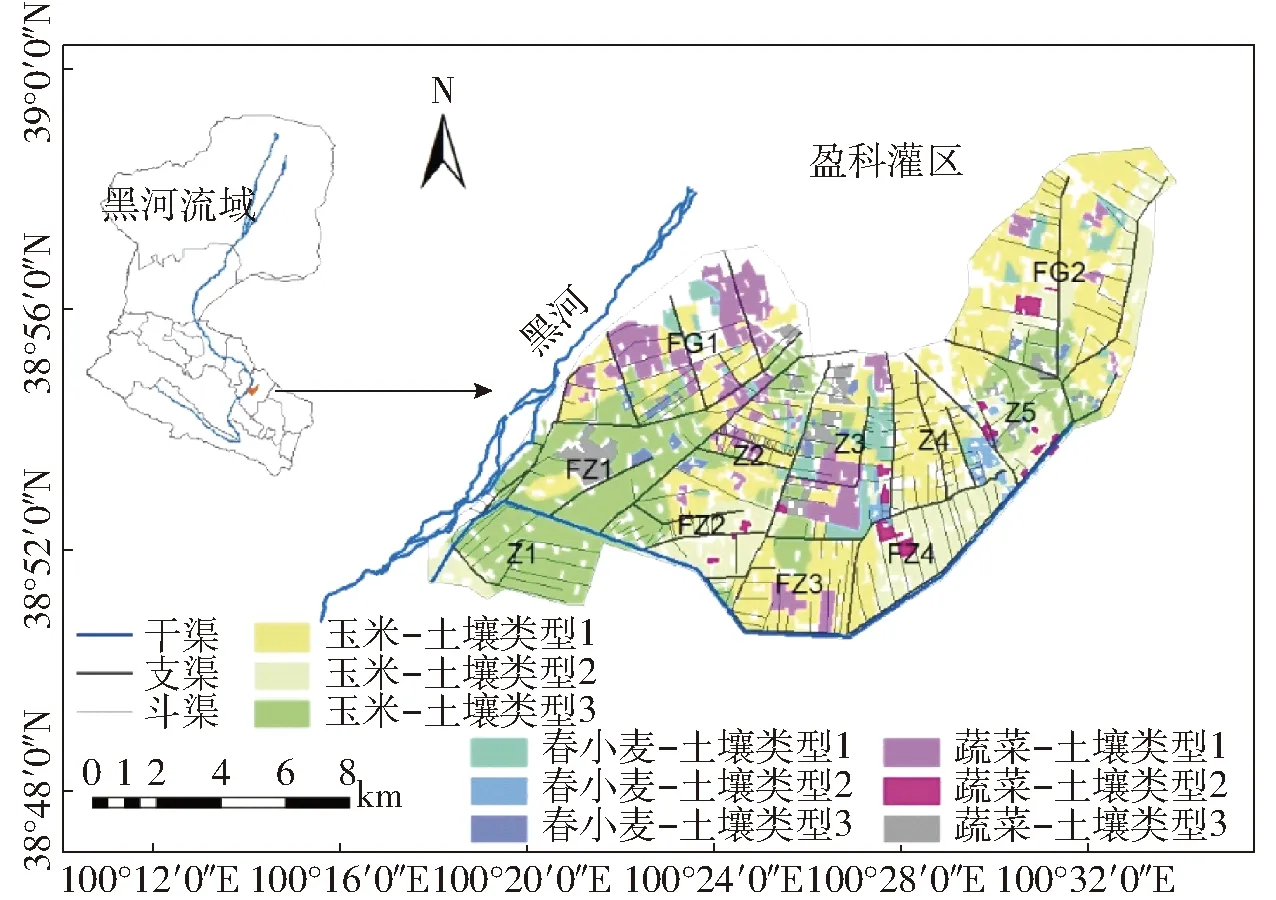
圖2 盈科灌區渠系及作物-土壤單元分布圖

2.2 模型參數設置

根據以往研究[23],灌區內土壤可分為3種類型,即粉壤土(0～140 cm)、壤土(0～140 cm)和粉壤土(0～60 cm),分別定義為土壤類型1～3。作物主要考慮玉米、春小麥和蔬菜(以包菜為代表)。根據灌區內3種土壤類型和作物的空間分布,共定義9種作物-土壤單元(圖2),對應9種類型CWPF(表1)。根據灌區渠系分布,共定義11個渠系控制區(圖2),作為優化模型第2層的子系統,各渠系控制區包含不同的作物-土壤單元,其內不同作物-土壤單元之間的優化為優化模型的第1層。優化模型中各參數設置參考文獻[23]。

表1 作物水分生產函數(CWPF)類型及其對應單元

為分析模型中不確定性參數的敏感性,共選取6類參數進行分析,分別為CWPF、水價、作物價格、作物種植成本、灌溉量約束和總可用灌溉水量(地表水和地下水),共計25個參數。其中,CWPF考慮由氣候變化引起的函數本身的不確定性,針對9種作物-土壤單元,分別利用1.2節所述模擬-優化模型[24]獲得不同氣候類型(適宜和不適宜)下的最優CWPF,其中,適宜和不適宜氣候年份參考文獻[24]分別采用2012年和2010年。以這2年的氣象數據驅動模擬-優化模型,從而確定各單元CWPF變化的上下限,如圖3(不同CWPF所對應土壤-作物單元及其分布見圖2和表1)所示。其他不確定性參數根據其現狀實際值進行上下浮動一定比例確定其取值空間,如表2所示。敏感性分析的輸出變量設定為優化模型的目標值——凈灌溉效益G和決策變量——作物灌溉量X和作物種植面積A。對25個參數分成10層進行LH抽樣(即M=25,N=10),對每個LH抽樣點采用OAT方法,模型總運行次數為10×(25+1)次,針對不同輸出變量,根據式(1)計算每個參數對應的敏感度。

表2 模型待分析參數及其取值

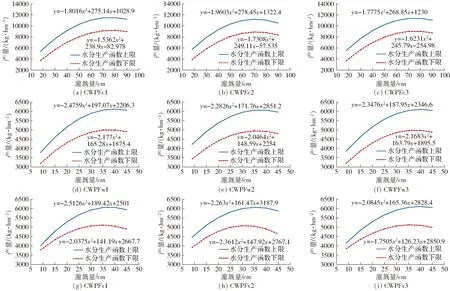
圖3 盈科灌區不同作物-土壤單元內作物水分生產函數

2.3 敏感性分析結果

針對不同輸出變量,計算得到25個參數的全局敏感度(圖4)及其排序(表3),將各參數對不同輸出變量的敏感度排序最小值作為其敏感度全局排序(表3)。參考文獻[16]及參數敏感度全局排序結果,將參數敏感性劃分為4個等級,排序為1的定義為極敏感參數,排序為2～5的為較敏感參數,排序為6～10的為一般敏感參數,排序在11及以后的為不敏感參數。

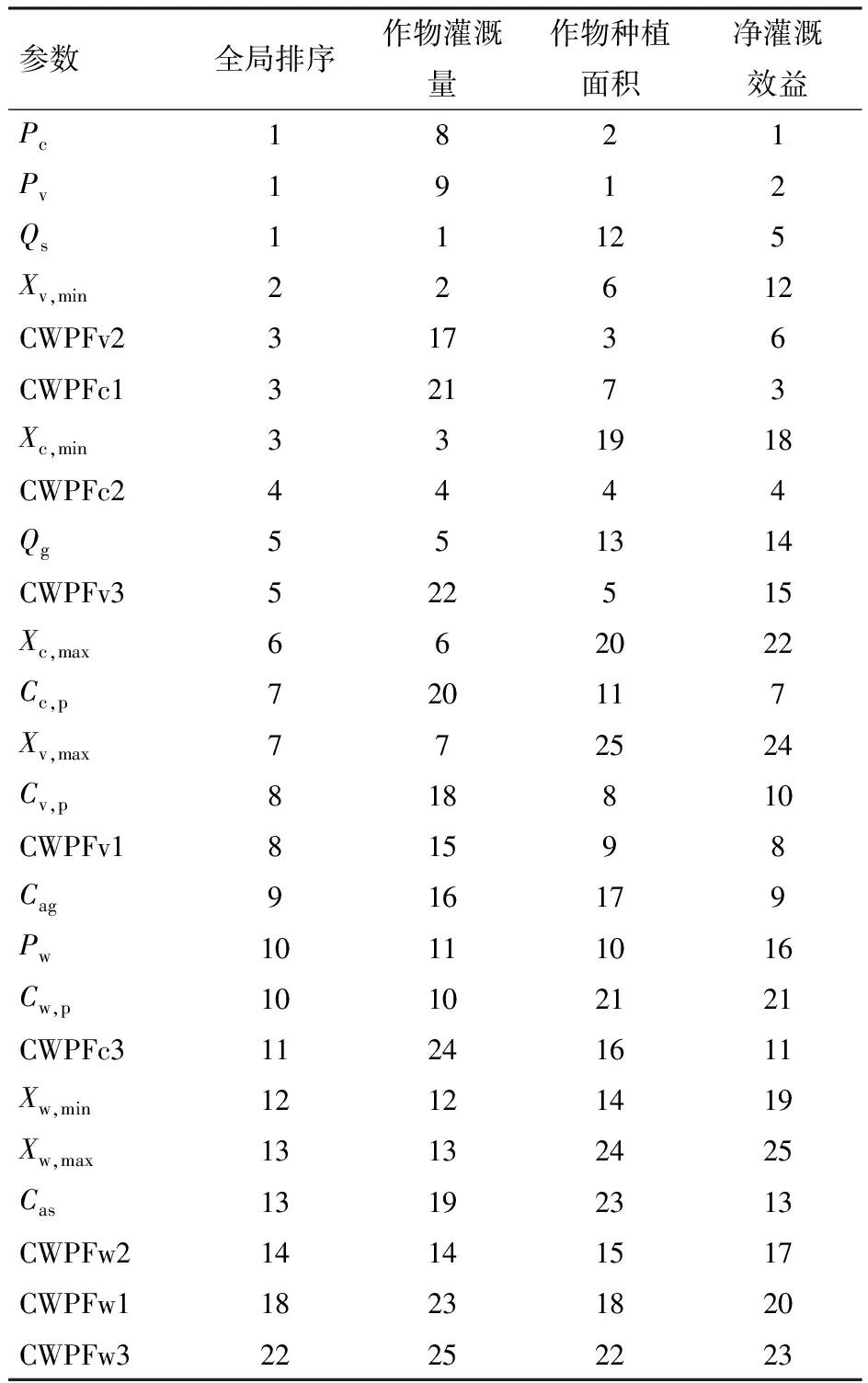
表3 參數敏感度排序

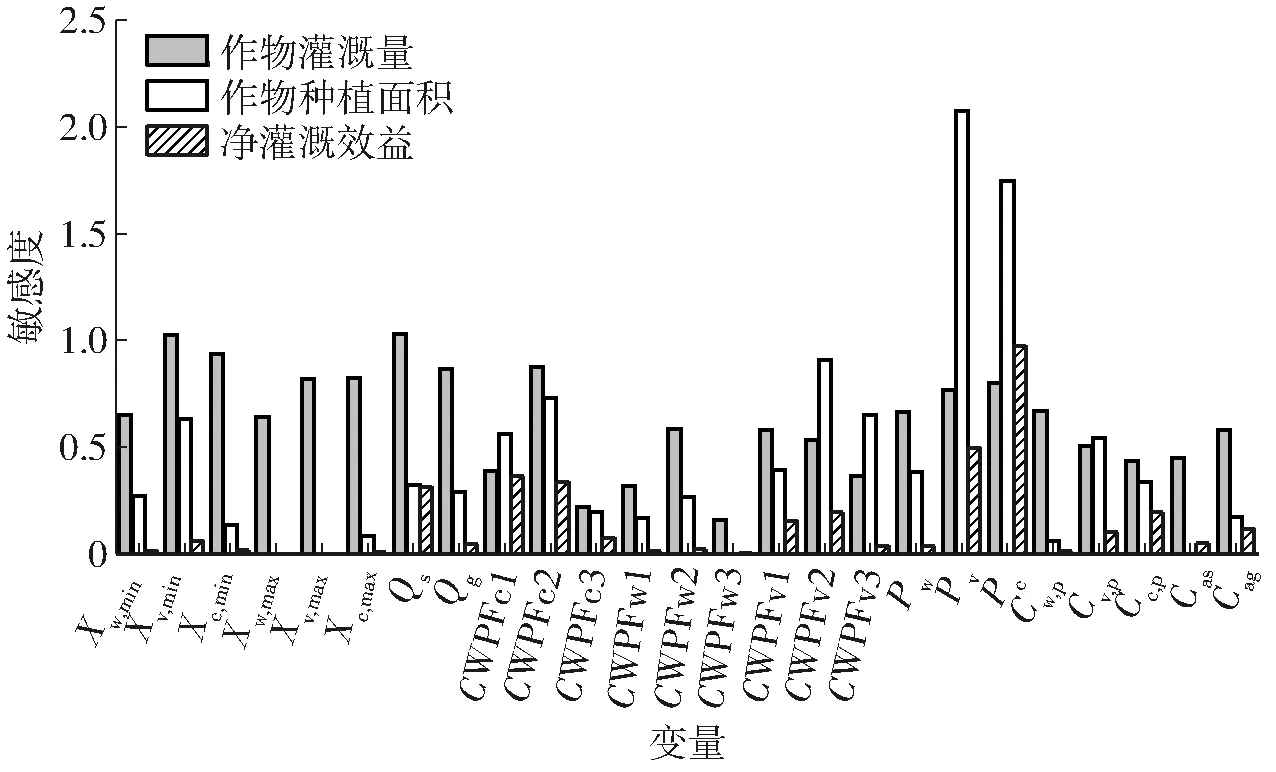
圖4 不同輸出變量的參數敏感度計算結果

2.3.1參數對決策變量的敏感性分析

以作物灌溉量X為輸出變量時,其對總地表水灌溉量Qs和蔬菜最小灌溉量約束Xv,min最為敏感,敏感度超過了1.0,對總地下水灌溉量Qg和其他灌溉量約束(Xmin和Xmax)均有較強敏感性,敏感度多大于0.8(圖4),這與實際情況相符合,即可用水量與灌溉量約束直接影響優化時作物灌溉量的分配。同時,作物價格P對X也有較大的影響,其敏感度為0.6～0.8,排序為8～11(圖4和表3),表明在優化過程中作物價格會通過影響灌溉收益來影響灌溉量分配。相較上述參數,X對CWPF的敏感度總體較小,平均敏感度小于0.5(圖4),排序主要在15以后(表3)。X對Cag的敏感性強于Cas,這可能是由于地下水價高于地表水價,地下水價波動對X的影響更大。總體上,X受模型輸入參數的影響較大,很多輸入參數對X的敏感度大于0.5。

以作物種植面積A為輸出變量時,其對作物價格P,尤其是蔬菜和玉米的價格(Pv和Pc)非常敏感,敏感度大于1.0,其次對部分CWPF、作物種植成本Cp和最小灌溉量約束Xmin也呈較強敏感性(圖4和表3)。對于同類參數,A對春小麥相關參數的敏感性較蔬菜和玉米的同類參數低(圖4和表3),這可能是由于蔬菜和玉米的價格和產量較春小麥高,在優化中考慮到效益最大化的問題,蔬菜和玉米的種植面積分配優先于春小麥。總體上,A對CWPF、P、Cp和Xmin的敏感性明顯大于其他參數,表明作物種植面積的分配與作物產量及其收益更密切。

2.3.2參數對目標值的敏感性分析

以目標值凈灌溉效益G為輸出變量時,其對玉米價格Pc呈極敏感,對Pv、Qs、CWPFc1和CWPFc2均呈較強敏感性,對地下水價格Cag、作物種植成本(Cc,p和Cv,p)、CWPFv1和CWPFv2呈一般敏感性。總體上,G對CPWF和價格相關參數都有不同程度的敏感性,這是由于作物產量和價格相關參數直接影響凈灌溉效益。然而,相較于蔬菜和玉米,G對與春小麥有關的所有參數均不敏感,這是由于春小麥的產量在3種作物中最小且價格偏低,即其潛在灌溉收益最低,導致優化中春小麥對灌溉效益的影響最小,故其相關參數也最不敏感。另外,G對Qg不敏感,但對Qs呈敏感性,這是由于在優化中地表水灌溉量大約是地下水灌溉量的3倍,且地表水價較低,在優化中具有優先性,故地表水灌溉量的不確定性會對作物灌溉配水帶來較大影響,進而影響凈灌溉效益。

2.3.3參數敏感性全局分析

參數敏感度全局排序結果表明,玉米和蔬菜的價格(Pc和Pv)、總地表水灌溉量Qs為3個極敏感參數(表3中排序為1)。其中,Pc和Pv對X的影響較小,但對G和A的影響明顯,而Qs對于X極敏感,但對于G和A較敏感,因此綜合考慮參數對于不同輸出變量的敏感性,上述3個參數均表現為極敏感。較敏感參數有7個,涵蓋了最小灌溉量約束(Xv,min、Xc,min)、4種類型的CWPF以及總地下水灌溉量Qg(表3中排序為2～5)。一般敏感參數共有8個,包括各作物種植成本Cp、地下水價格Cag、玉米和蔬菜的Xmax以及春小麥價格Pw和1類CWPF(CWPFv1)(表3中排序為6～10)。總體上,作物價格、玉米和蔬菜的CWPF、總可用灌溉水量以及最小灌溉量約束的敏感性較強,其不確定性對優化模型的影響較大。

2.4 優化結果分析

根據參數敏感度全局排序,選取極敏感和較敏感參數(即全局排序1～5)作為優化模型的不確定性輸入參數,包括部分作物價格(Pc和Pv)、部分CWPF(CWPFc1、CWPFc2、CWPFv2和CWPFv3)、部分灌溉量約束(Xv,min和Xc,min)以及總可用灌溉水量(Qs和Qg)共計10個參數,其他參數則不再考慮其不確定性,仍參照以往研究設置[23]。根據灌區實際情況,設置10個不確定性參數的變動范圍,其中CWPF的變動范圍仍參考圖3,其他參數的變動范圍如表4所示。對所選10個不確定性參數,在其變動范圍內采用LH抽樣法隨機生成N個參數組(N≥20,每組包含10個參數),作為優化模型的不確定性參數輸入,以此最終得到灌區用水的不確定性優化結果。

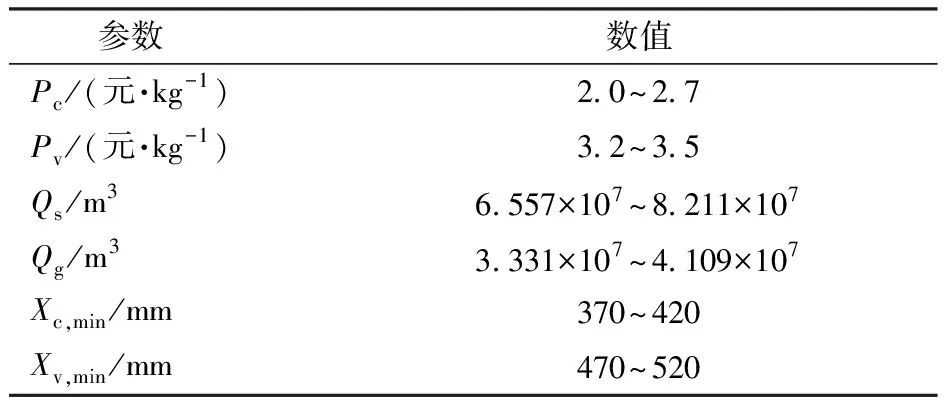
表4 優化模型敏感性參數變動范圍

由圖5可以看出,不同渠系之間的配水量存在明顯空間差異,同時由于不確定性參數的影響,同一渠系的配水量也存在明顯波動,如控制區Z4的地表水和地下水配水量分別為188.4～370.7 mm和32.2～221.8 mm,表現出較大的不確定性。同時,可注意到,地下水配水量的波動比地表水更明顯,這可能是因為地下水水價較高,對灌溉效益影響更大,因此其價格的不確定性引起地下水配水量較大的波動。另外,部分渠系的地表水配水量波動很小,如FZ3、FZ4、FG1和FG2,這可能是這些渠系控制區的單方水效益較低,其配水量往往傾向分配最小值,受參數不確定性的影響較小。

圖5 各渠系控制區灌溉配水量優化結果

不同渠系控制區內各作物種植面積優化結果如圖6(圖中C、W和V分別表示玉米、春小麥和蔬菜)所示。從圖6可以看出,各渠系控制區內玉米和蔬菜的種植面積比春小麥的種植面積波動更明顯,這主要是由于春小麥產生的經濟效益偏低,優化中種植面積往往會優先分配給玉米和蔬菜這些高效益作物,因此其受敏感參數不確定性的影響更大。同時,不同渠系間的作物種植面積分配及其波動也存在明顯差異,這主要與控制區內作物-土壤單元分布有較大關系。

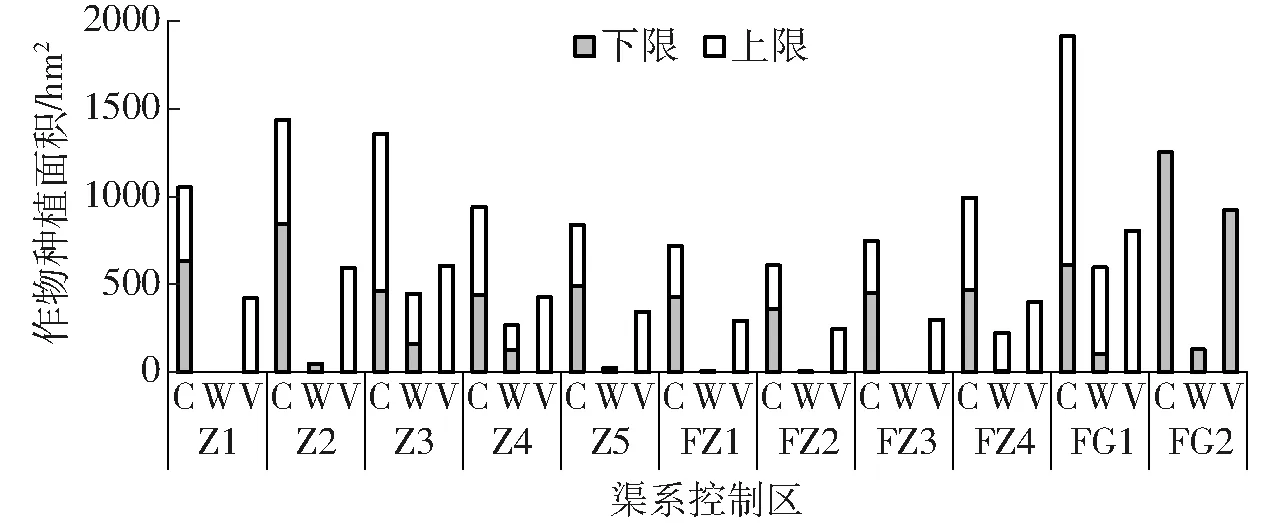
圖6 各渠系控制區作物種植面積優化結果

圖7為不同渠系內不同作物灌溉量的優化結果。由圖7可知,各渠系之間作物灌溉量呈現出較大差異,如控制區Z1內的玉米灌溉量為57.0～69.3 mm,而控制區FZ4內的玉米灌溉量僅為40.0～44.2 mm。相比而言,玉米灌溉量的空間差異較蔬菜和春小麥明顯,如春小麥灌溉量在許多渠系控制區幾乎一致,這也與各作物的經濟效益密切相關。由于不確定性參數的影響,各渠系內作物的灌溉量也表現出明顯波動,但由于不同渠系內基本參數(如作物和土壤分布)等的差異,作物灌溉量的波動幅度在不同渠系之間呈現出較大不同,如控制區Z2內的蔬菜灌溉量為49.3～88.8 mm,呈現出較大不確定性,而一些渠系控制區內的蔬菜灌溉量波動為50 mm左右,春小麥的灌溉量幾乎不變。

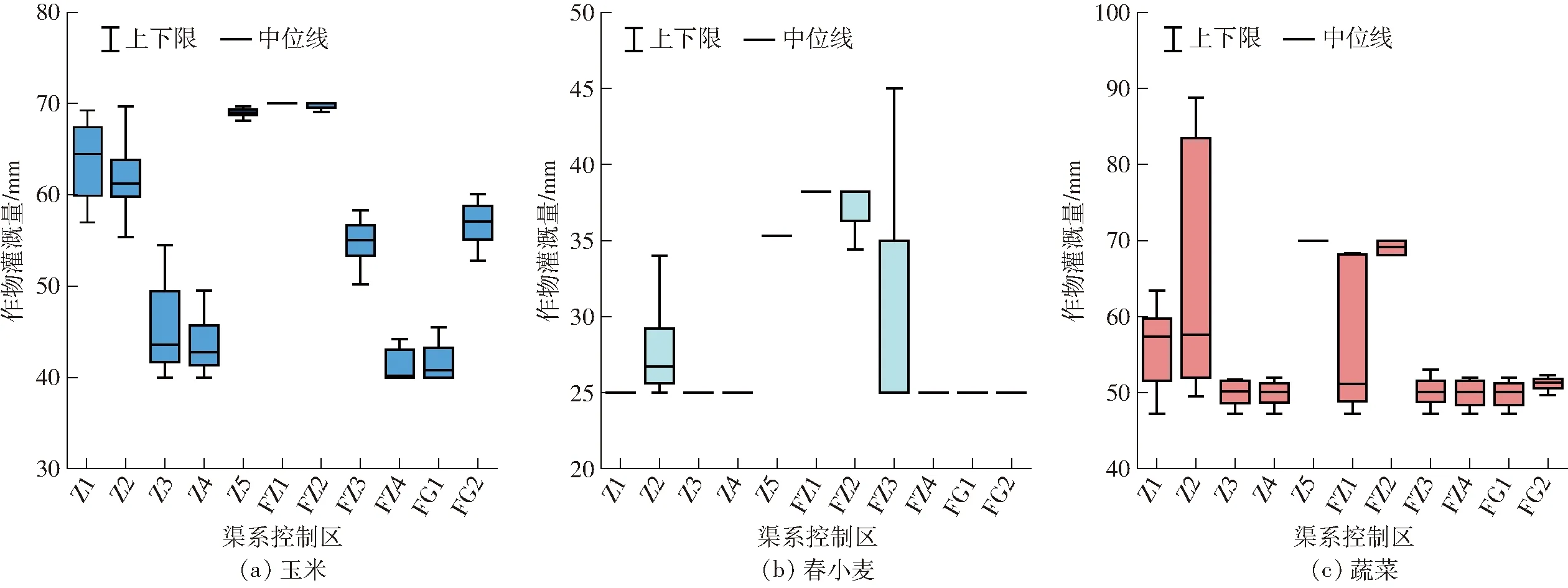
圖7 各渠系控制區內各作物灌溉量優化結果

3 討論

案例分析表明,本文所提出的基于LH-OAT的灌區用水優化模型敏感性分析與不確定性優化方法可以合理且高效地識別出高敏感性參數,并能夠反映出多種敏感參數及其不確定性對優化結果的綜合影響,是分析優化模型中不確定性參數全局敏感性的有效可行方法。其優勢具體表現為:

(1)以往灌區水資源優化配置研究很少對模型中參數的敏感性進行定量分析,這不僅容易影響結果分析的準確性,而且在構建不確定性優化模型時,容易忽略部分敏感性參數的不確定性及其對優化結果的影響。本文將LH-OAT方法與灌區用水優化模型耦合,對優化模型中涉及的眾多不確定性參數進行全局敏感性分析,以此獲得各參數的敏感度排序,并篩選出高敏感參數作為不確定性參數輸入,從而較全面地考慮了優化模型中的敏感性參數及其不確定性,且計算效率較高,具有實用性。

(2)相比以往灌區用水不確定性優化模型僅考慮某幾個不確定性因素并予以量化表征,本文所提出方法可較全面地同時考慮多種敏感性參數的不確定性,通過這些參數的隨機采樣和組合,開展不確定性下的灌區用水優化。這種方式一方面不再需要分析不確定性參數的特征或分布規律來對其進行量化表征,從而降低了模型的復雜性,提高了優化計算的效率;另一方面優化結果能反映眾多敏感性參數的綜合影響,而不僅僅是某一因素的單一影響。

4 結論

(1)針對灌區水資源優化配置過程中存在眾多不確定性參數而影響模型效率的問題,將LH-OAT方法與灌區用水優化模型耦合,構建了基于LH-OAT方法的灌區用水優化模型參數敏感性分析與不確定性優化方法。將該方法應用于黑河流域中游盈科灌區的灌溉用水優化中,分別以優化模型的目標值——凈灌溉效益G和決策變量——作物灌溉量X和作物種植面積A為輸出變量,以6類共25個不確定性參數為輸入變量,定量確定了各參數針對不同輸出變量的敏感度及其全局排序,篩選出10個高敏感性參數,并將高敏感參數作為模型不確定性參數輸入,獲得了不確定性下的灌區用水優化結果。

(2)各參數對不同輸出變量的敏感性存在差異,綜合考慮各輸出變量,極敏感參數為玉米和蔬菜的價格及總地表水灌溉量,較敏感參數涉及蔬菜、玉米最小灌溉量約束、4種類型的作物水分生產函數以及總地下水灌溉量,合理反映出不確定性參數對優化結果的綜合影響。

(3)基于高敏感性參數的灌區用水不確定性優化高效可行,較全面地考慮了高敏感的不確定性參數,從而大大降低不確定性下優化模型結構和求解的復雜性,提高模型效率,并且能綜合考慮多種不確定性參數對優化結果的影響,為灌區水資源優化配置研究提供了實用且有效的方法參考。