封裝工藝對電樞熱導率影響的實驗研究*

李兆宗，張承寧，章恒亮，張 碩

（1.北京理工大學機械與車輛學院，北京 100081；2.東南大學電氣工程學院，南京 210096；3.諾丁漢大學電氣工程學院，英國 諾丁漢 NG7 2GT）

前言

近年來，隨著電動車驅動技術的多樣化發展，在集中驅動結構中應用的高轉速電機［1-2］和在輪轂電機結構中應用的高轉矩電機［3-4］同時成為汽車領域廣泛應用的電機類型。因此，在傳統圓形漆包線繞組的基礎上，發卡繞組（扁銅線）和絞線繞組電機同時孕育而生。發卡繞組的優勢在于可以降低電機在低速工況下的直流損耗［3］，能夠有效提高電機在低速工作區間的工作效率。反之，絞線繞組應用的目的是通過緩解電樞中的趨膚效應和臨近效應以降低電機的交流損耗［4-5］，從而提高電機在高轉速工作區間的工作效率。常見的絞線電樞主要包括換位漆包線、圓形利茲線和矩形利茲線等結構。

相對于應用在靜態電力電子設備（如變壓器、電磁爐等）中的電樞結構，車用電機最顯著的特點在于其電樞大多具有封裝工藝，即通過對電樞灌注環氧樹脂等高性能非金屬材料以保證電機定子的結構強度和可靠性。圖1 所展示的電樞為封裝后的利茲線電樞。本文設定圖中z軸方向為電樞軸向，x、y為電樞的截面方向。

電機電樞的熱管理是提高車用電機性能的關鍵，也是保障電機可靠性的基礎。因此，準確計算電樞的熱導率是建立模型必不可少的前期工作。在此，為評估各類計算車用電機電樞熱導率方法的優勢和局限，文中匯總了國際上10 篇有代表性的文獻以便讀者參考，如表1所示。

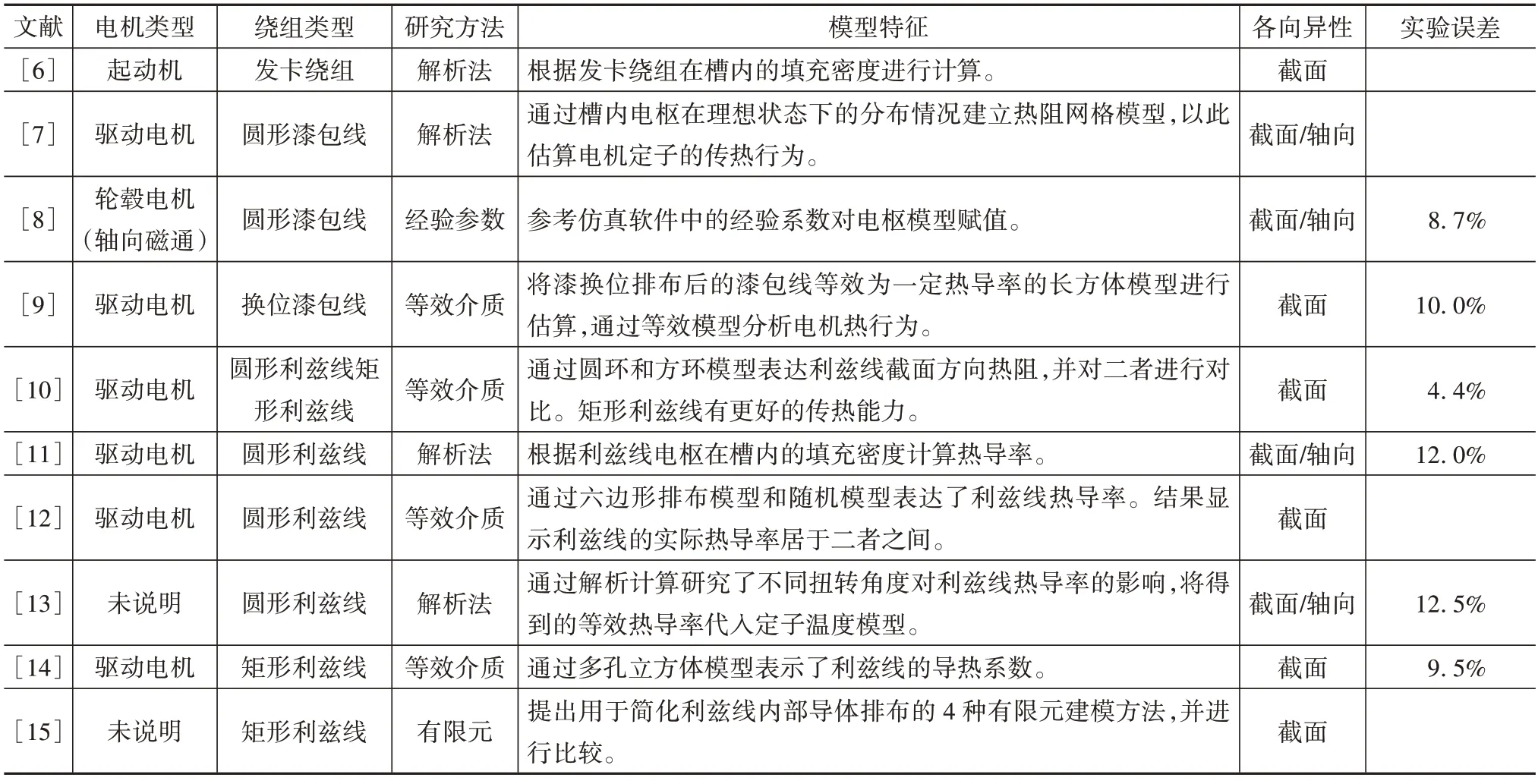
表1 車用電機各類電樞熱導率計算方法匯總

通過對表1中文獻的總結，可以得出目前電機設計者對電樞軸向熱導率預測存在的如下3點局限。

（1）各向異性研究不充分 各類電樞的軸向熱導率研究不如截面方向的熱導率研究充分，軸向熱導率普遍采用經驗參數或電樞的填充密度作為估算電樞軸向熱導率的依據。然而，由于高頻電機中的電樞通常會具有獨特的絞合結構，封裝工藝對其傳熱效率的影響也將比傳統圓形繞組更加明顯，須仔細考慮。

（2）模型精度不足 包括換位漆包線和利茲線在內的絞合電樞的熱導率解析計算結果誤差在10%以上，仍有一定的優化空間。同時，隨著電機種類的多樣化，端部油冷電機以及軸向磁通電機應運而生［4-5］。在這些電機的拓撲結構中，其電樞中大部分的熱量都是通過軸向散發，因此須對電機建立三維模型才能得到更精確的預測結果。然而，面對復雜的絞合電樞結構，傳統的軸向熱導率估算方法是無法滿足精度要求的。

（3）工藝考慮不足 各類電樞軸向熱導率的模型均未涉及封裝工藝對電樞傳熱特性的影響。然而，在日益提升的非金屬材料導熱性質面前，直接忽略非金屬材料的熱導率不夠嚴謹。上述文獻中所有的模型均無法表達電樞內部漆包線之間的傳熱性質，所以很難在模型中體現出電樞在封裝后的熱導率變化，這種直接忽視封裝工藝的計算方法在車用電機中需要得到更新。

因此，本文提出一種能夠表達車用電機電樞軸向熱導率的數學模型，并能夠得到電樞在封裝后更加精確的熱導率。然而，由于目前沒有評估封裝工藝對熱導率影響的文獻能夠作為參考，所以本文選擇從實驗的角度出發，首先通過實驗數據得到電樞真實的物理性質，而后通過對電樞的結構特點和實驗數據分析對其建立相應的數學模型，以保證高效準確地實現各類電樞軸向熱導率的預測。

1 各類電樞的結構特點

選取的9款電樞樣品如圖2所示，其關鍵參數的詳細信息匯總在表2中。

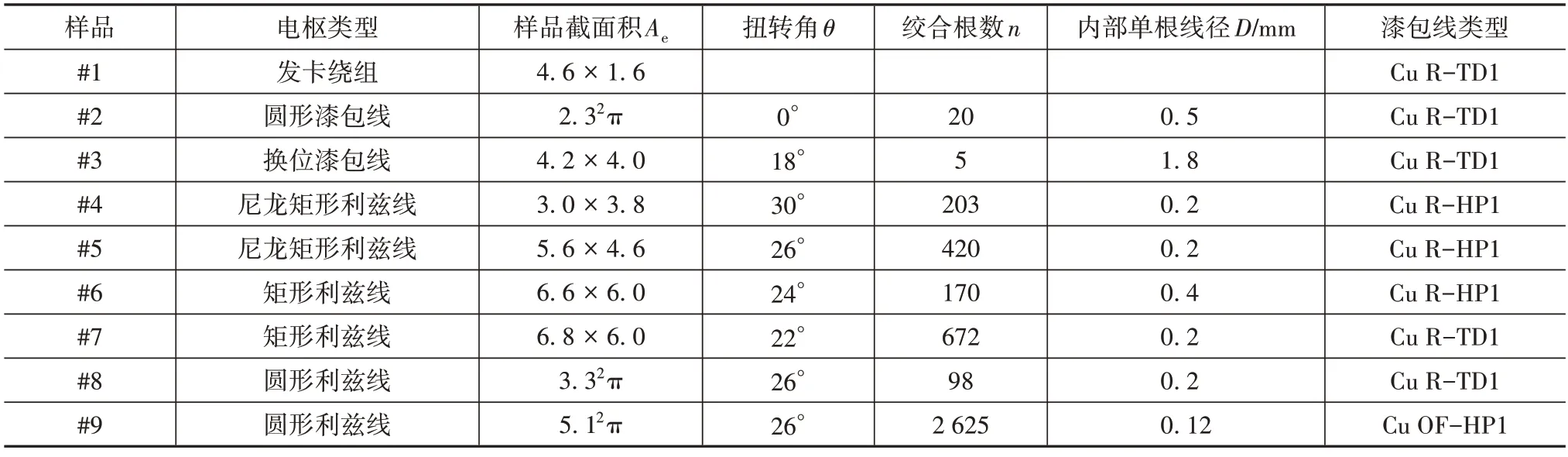
表2 樣品信息

圖2 電樞樣品

在表2 中，電樞類型是指其加工工藝帶來的不同性質。目前市面上應用的電樞主要包括絞合和塑形（壓縮）兩種加工工藝。電樞的絞合通常會經歷1～3 次，根據漆包線絞合次數的不同，它們分別被稱為“換位漆包線”、“利茲線”和“多層利茲線”。同時，為實現更高的槽滿率，各類電樞也會被壓縮為適用于各類電機的矩形截面。其工藝流程以及樣品#1～#9所歸屬的類型如圖3所示。

圖3 各類電樞的加工流程

電樞的截面積Ae如圖3 中的虛線框所示。電樞中的扭轉角θ為各類絞線的扭轉角，其物理意義如圖4所示。

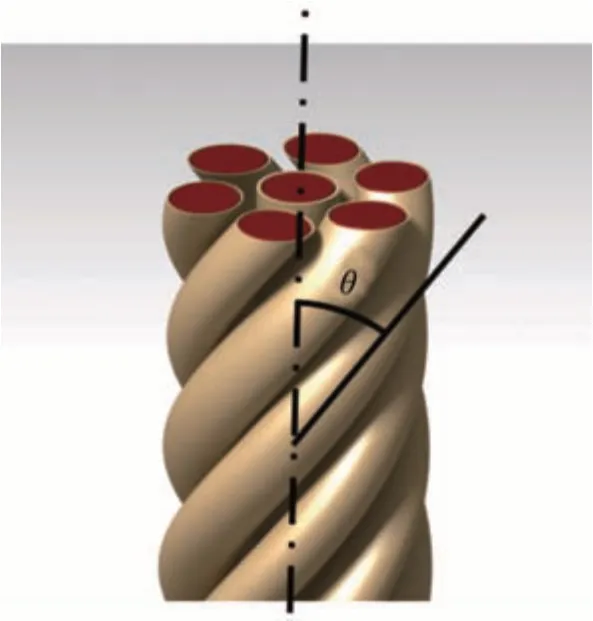
圖4 電樞的扭轉角θ

絞合根數n和單根線徑D指的是絞線內部漆包線的總數和單根漆包線的直徑。漆包線類型中涉及的漆包線與封裝材料的物理性質均來自于樣品的參數表，本文中所需的材料信息匯總于表3。

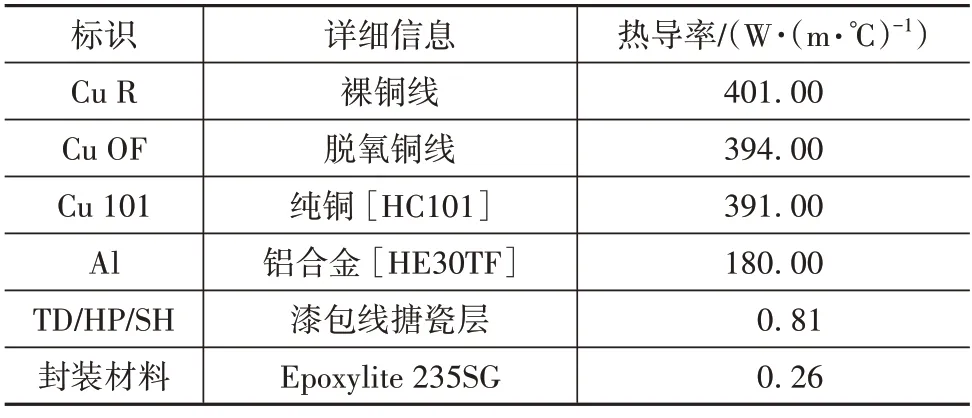
表3 材料熱導率信息

值得注意的是，為更好地復現封裝材料對電樞熱導率的影響，文中使用目前車用電機最常見的非金屬固化劑［Epoxylite 235SG］作為各類電樞的灌封材料，以更好地對比封裝工藝對電樞熱導率的影響。文中所有電樞樣品的封裝工藝均模擬車用電機標準，在施加預緊力的條件下進行真空浸漬（vacuum casting），從而改善電樞內部漆包線之間的接觸條件，增強換熱效率。以樣品#4 為例，真空浸漬后的電樞樣品如圖5所示。

圖5 封裝后的樣品#4

2 軸向熱導率測定實驗

面對電樞多樣化的內部結構，設計者通常很難直接建立導體內部的傳熱模型，更難以直接通過解析計算評估封裝工藝對各類電樞熱導率的影響。為提高建模效率，首先對封裝前后的電樞的軸向熱導率進行測量。

2.1 實驗臺架設計

電樞軸向熱導率的實驗臺架原理如圖6所示。

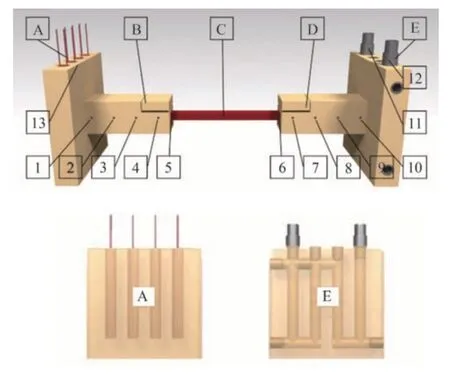
圖6 樣品測量原理

圖中A 為嵌有加熱器的銅板，用恒定的熱源控制溫度。夾具B 和D 用來固定電樞樣品C，夾具B 和夾具D 的形狀相同。E 為內部有冷卻液通道的銅板。臺架中部件A、B、D 和E 均使用銅［HC101］制作而成。點1～13 為測溫通道。通道1、2 和3 之間的溫差可以用來計算流經B 的熱流qB，通道8、9 和10 可以用來計算流經D 的熱流qD。通道4 和6 的溫度可以用來檢查樣品與B 之間的接觸。通道5 和通道6用來獲取樣品C 兩段的溫度差，從而計算出通過樣品的熱流密度。通道11 和12 分別對應冷卻劑進口和出口溫度，用于監測冷卻液的實時溫度。通道13用來測量熱板A的溫度和PID恒溫熱源的功率控制。

在熱穩定條件下，流經B 的熱流密度qB應等于流經D 的熱流密度qD，且與流經C 的熱流密度qC相同。計算樣品軸向熱導率的方法為

式中：AB和Ae分別為夾具B 和待測樣品C 的截面積，mm2；λCu為銅［HC101］的熱導率，W/(m·℃)；ΔTi，j為i點與j點之間的溫差，℃；Δxi，j為i點與j點之間的物理距離，mm；λSample為每個樣品中待測熱導率，W/(m·℃)。

基于上述原理，實驗在樣品和實驗臺上包裹了絕熱層，緩解樣品向外界的散熱。實驗臺表面覆蓋的隔熱層為鈣鎂硅酸絕熱片，最外層為泡沫箱。成品實驗臺和溫度采集器如圖7所示。

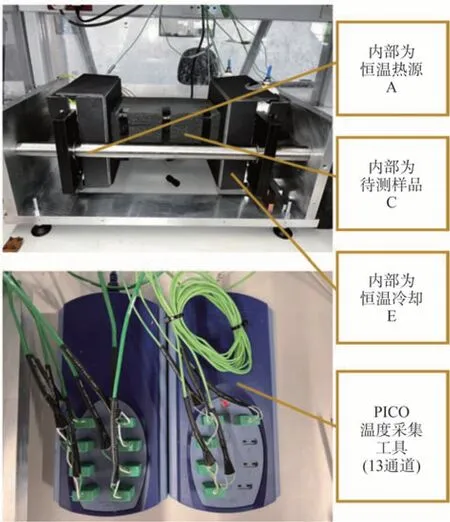
圖7 實驗設備實拍圖

2.2 實驗臺架的誤差標定

由于需要討論封裝工藝對各類電樞的未知影響，所以實驗臺架的測量值需要較高的精度，以保證后續分析的有效性。

基于上述的實驗原理，熱導率測量的誤差將來自兩個方面，一個是熱電偶的測量誤差，另一個是實驗臺之間的散熱。因此，首先對式（2）熱導率計算式進行改寫，并引入兩個修正系數kd和δij作為臺架補償系數，公式為

式中：kd為臺架的散熱補償系數；δij為熱電偶誤差補償系數。

臺架的誤差補償系數kd須通過建立散熱模型進行計算，如圖8所示。

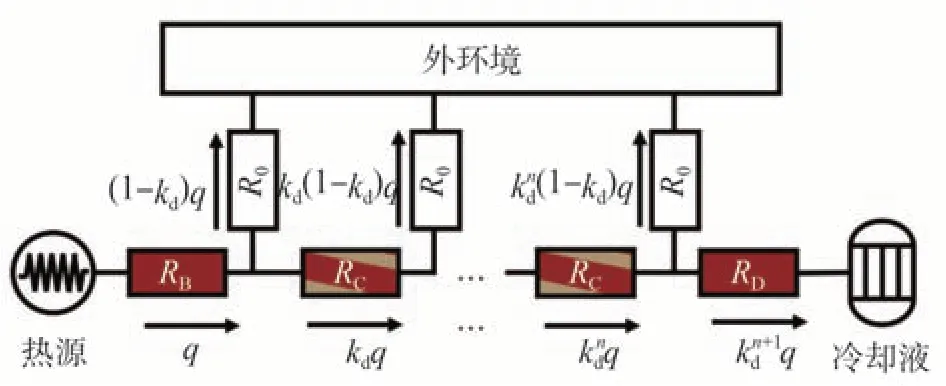
圖8 實驗臺架的散熱模型

圖中RB、RC、RD和R0分別代表夾具B、樣品C、夾具D 和絕熱層的熱阻。假設實驗臺架可劃分為n段，每段的絕熱條件相同，且外部環境溫度一致。則可以假定的熱量繼續沿導體傳遞，而的熱量則向外傳遞。因此，為求解上述未知數kd，需要使用多個性質已知的樣品作為標定。校準過程中，分別使用200和150 mm的銅［HC101］（熱導率為391 W/（m·℃））和鋁合金［HE30TF］（熱導率為180 W/（m·℃））金屬條作為標定樣品，以保證所有的利茲線樣品的熱導率經驗值范圍均處于391～180 W/（m·℃）之間，如圖9所示。

圖9 標定樣品

對于每個標定用的樣品，臺架分別將A 銅板設置為50、70、90 ℃ 3 個溫度，E 銅板保持在10 ℃，并在上述條件下重復多次測量通過qB和qD的差值，依據圖8 中的散熱路徑圖求取平均值后計算臺架的散熱系數kd。

熱電偶的誤差補償系數δij通過熱水浴進行標定。其具體方法為：分別記錄下通道1～4處于i溫度條件時各熱電偶的誤差δi，以及通道8～10處于j溫度條件下各熱電偶的誤差δi，從而得到夾具上8根熱電偶在加熱端溫度為i、制冷端溫度為j條件下的誤差δij作為后續計算的熱電偶補償系數，如圖10所示。

圖10 熱電偶的水浴標定

在得到實驗臺架的kd和δij兩個補償系數后，再次參照上述實驗條件測量圖11 中100 mm 的兩個標定樣品。

圖11 標定樣品

圖11 中銅條樣品在點1～10 的溫度收集結果如圖12（a）所示，鋁條樣品在點1～10 的溫度收集結果如圖12（b）所示。銅條和鋁條熱導率計算結果如表4所示。

表4 臺架標定結果

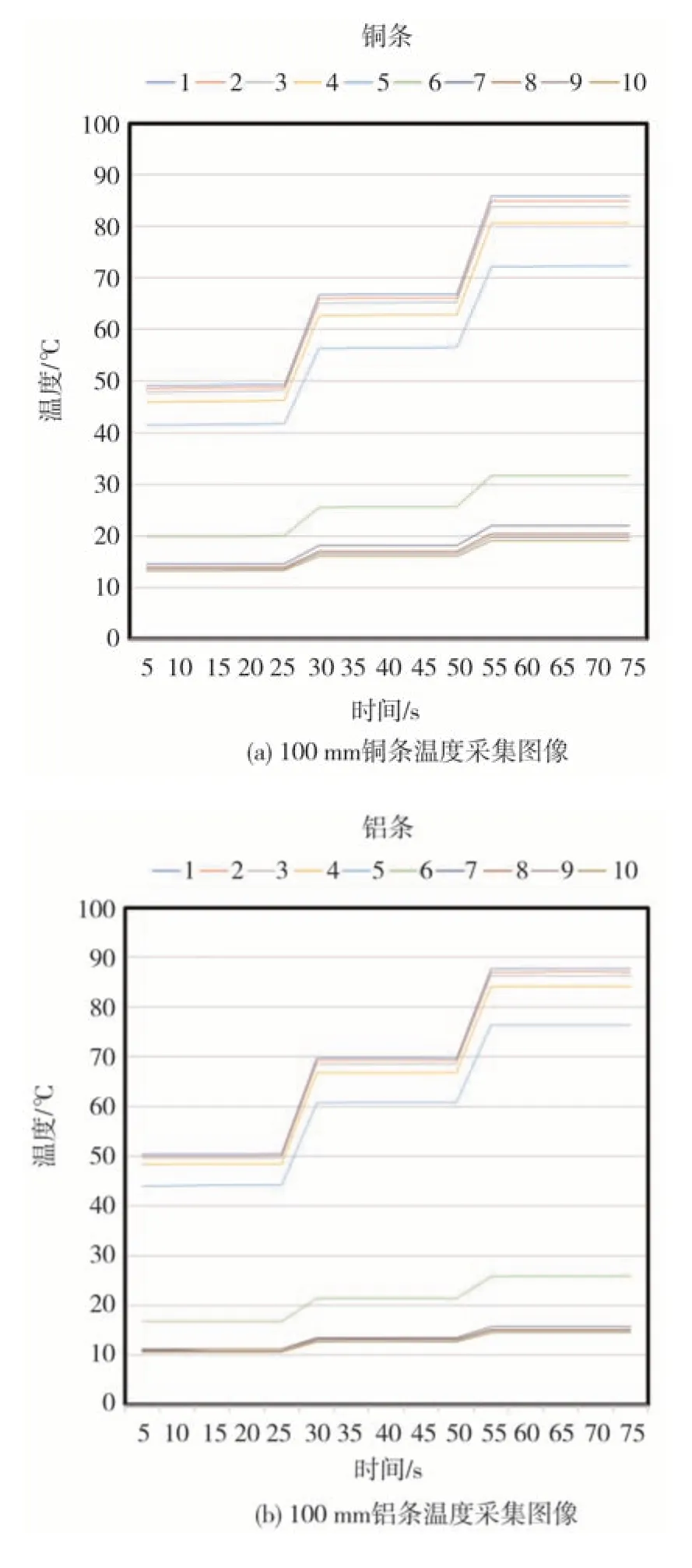
圖12 標定樣品溫度采集結果

通過對標準材料Cu ［HC101］和Al ［HE30TF］樣品的標定，在后續測量100 mm 樣品的實驗中，實驗臺架展示出良好的準確性。通過表4 可以看出，該實驗臺的誤差可以將待測樣品的導熱系數誤差控制在0.7%以內，具有足夠的參考價值。

2.3 測量結果

在標定實驗臺架后，該實驗臺配合補償系數測得9 個樣品在封裝前后的熱導率，并計算得到封裝工藝對其熱導率產生的影響。在驗證過程中，冷卻液溫度固定在10 ℃，A 的溫度控制在50、70、90 ℃3 個不同的溫度。同時，實驗過程中，為保證各個樣品測量結果的準確性，每款電樞均加工了多個樣品，且測量時會將樣品的“加熱端”和“制冷端”調換一次，分別記錄兩次的溫度梯度數據，以消除樣品兩端可能出現的尺寸差異。實驗結果如表5 所示，并繪制如圖13所示的柱狀圖作為更好的參考。

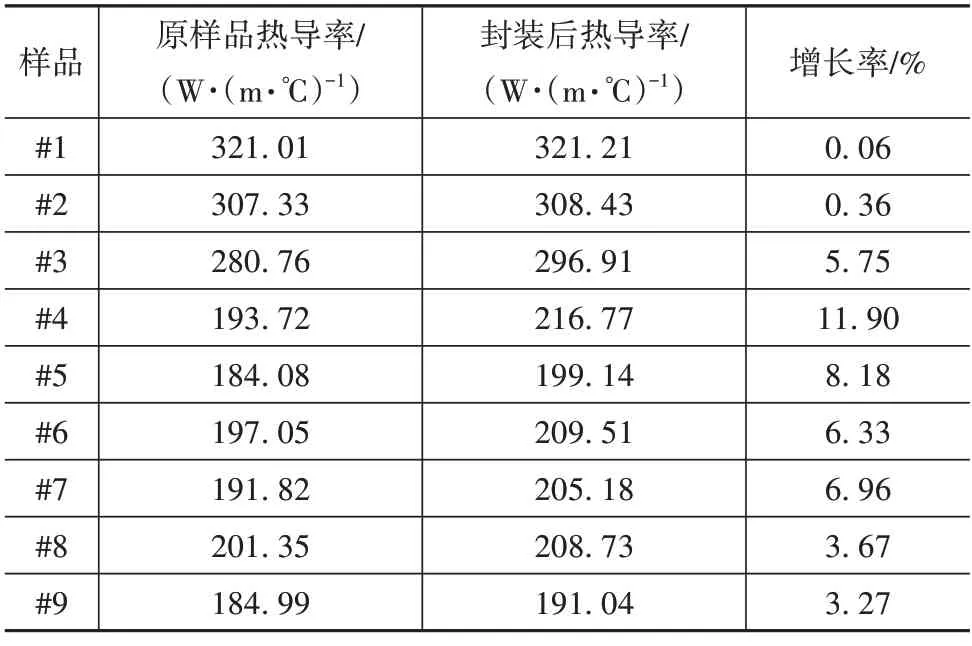
表5 實驗結果

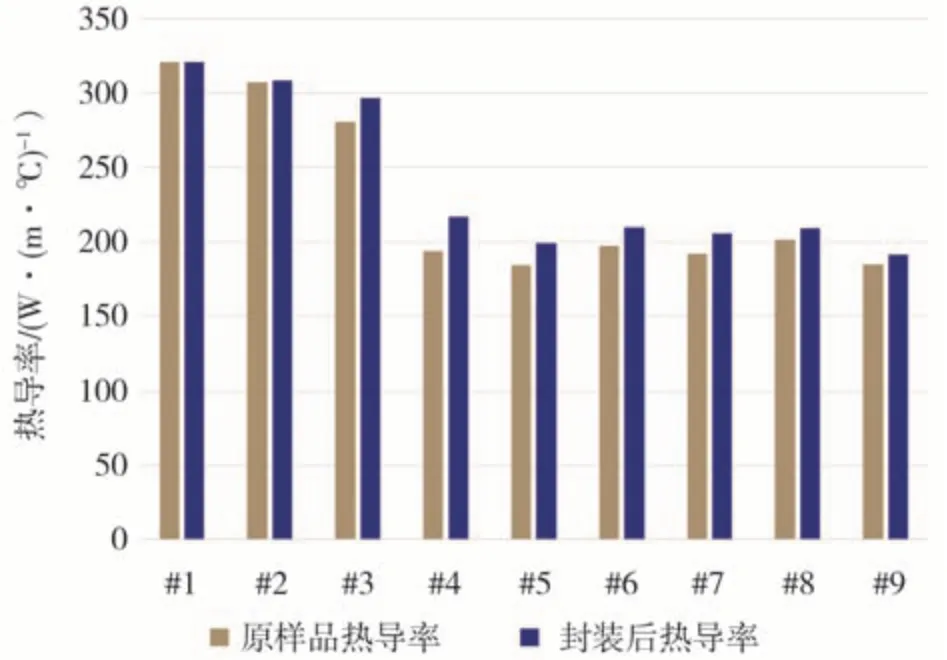
圖13 樣品封裝前后熱導率對比

通過對各類電樞封裝前后熱導率的對比，可以發現非金屬封裝材料對電樞軸向熱導率起到的影響不能忽視。但是，對于樣品中的發卡繞組和圓形漆包線而言，其影響相對較小。反之，對于包括換位漆包線和利茲線在內的各類絞線的影響卻非常明顯。基于對實驗結果和傳熱理論的分析可知，圓形絞線是可以通過塑型工藝提升其軸向熱導率。其原因在于，塑形改變了漆包線之間的接觸情況，在微觀層面提升了各根漆包線之間的接觸面積，從而使電樞對真空浸漬工藝更加敏感。

3 封裝工藝影響的建模分析

對于實驗數據所展示出的兩種不同性質，將電樞樣品分為“平行電樞”和“絞合電樞”兩類，并基于其內部結構提出了兩種計算電樞軸向熱導率的方法。

3.1 平行電樞軸向熱導率模型

平行電樞（parallel winding）是指電樞內部的漆包線平行排列，不存在絞合工藝，主要包括發卡繞組和圓形漆包線等電樞種類。對于這類電樞，封裝工藝對其熱導率的影響來自軸向，即漆包線和封裝材料的熱導率處于并聯狀態，槽內的材料分布如圖14所示。

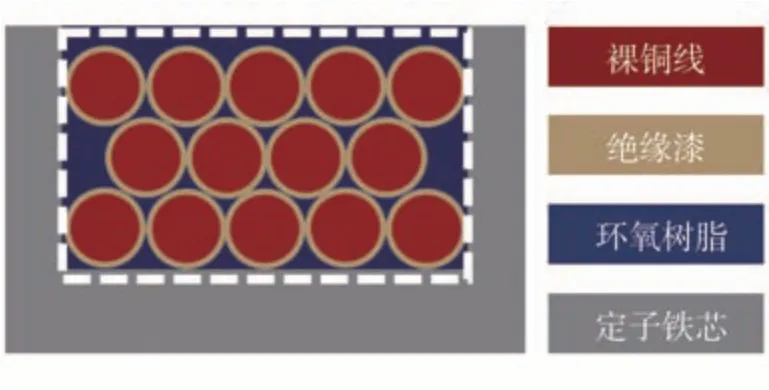
圖14 平行電樞槽內材料分布

圖中白色虛線框指齒槽截面積AS。因此，平行電樞的等效熱導率并聯模型如圖15所示。

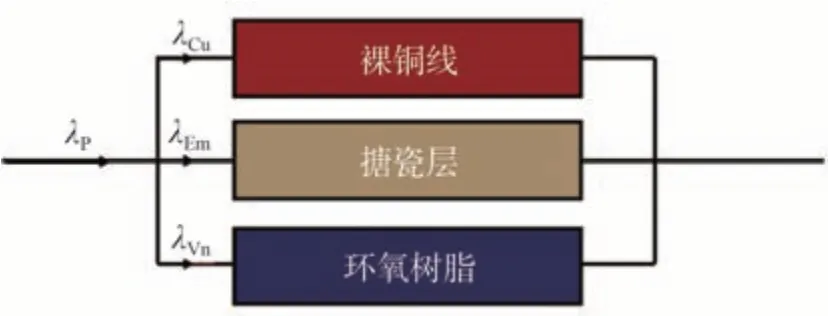
圖15 平行電樞熱導率模型

平行電樞的等效熱導率λP計算公式為

式中：λCu、λEm和λVn分別代表銅、漆包線搪瓷層和封裝材料的熱導率，W/(m·℃)；AS為齒槽截面積；ACu、AEm和AVn分別代表齒槽內部各種材料的截面積，mm2。模型中各材料熱導率均已知，因此只須知道各類材料在電樞內的體積占比即可獲得電樞的軸向熱導率：

式中：ff為電樞的槽滿率，可直接通過齒槽截面積和電樞的數量確定；σ為搪瓷層厚度相對漆包線中裸銅線直徑的比值，目前標準漆包線和發卡繞組的σ取值均為0.05。因此，平行電樞的槽內熱導率λP可以將σ代入式(4)后通過各材料占比計算，公式為

3.2 絞合電樞軸向熱導率模型

絞合電樞（twisted winding）是指將電樞內部的漆包線進行扭轉后制成的電樞，主要包括換位漆包線和利茲線等結構，其理想化的三維模型如圖16所示。

圖16 絞合電樞的理想結構

不難看出，無論是矩形絞線還是圓形絞線，各層導體在絞合后均呈現出平行狀態。因此為簡化模型，可以將一小段三維模型中的絞線模型展開，簡化為平形排布的電樞模型，從而構建微觀層面的傳熱模型，如圖17所示。

圖17 展開后的絞線模型

基于熱傳導規律，由于封裝材料的熱導率遠小于銅線內部的熱導率，因此封裝工藝的影響主要作用于漆包線之間的傳熱。相對于平行電樞結構，絞合后的電樞內部傳熱路徑不能直接以并聯關系進行計算。從微觀角度來看，絞合后的電樞內部出現漆包線之間的疊壓關系。在微觀模型中可以得到漆包線之間的傳熱與裸銅線中傳熱的幾何關系，其微觀傳熱路徑如圖18所示。

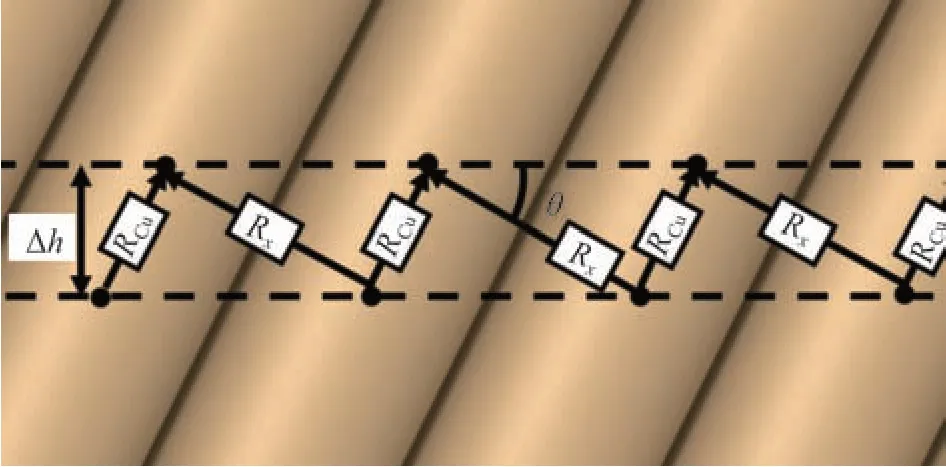
圖18 絞合電樞內部傳熱路徑

圖中：Δh為一小段電樞長度；RCu為裸銅線的熱阻；Rx為漆包線之間的熱阻，其等效熱阻的計算公式見式（9）。

式中：RT為絞合電樞熱阻，m2·℃/W；RCu為裸銅線熱阻，m2·℃/W；Rx為漆包線之間的熱阻，m2·℃/W。根據傅里葉傳熱定律，可對熱導率計算中所需的物理量建立幾何模型，如圖19所示。

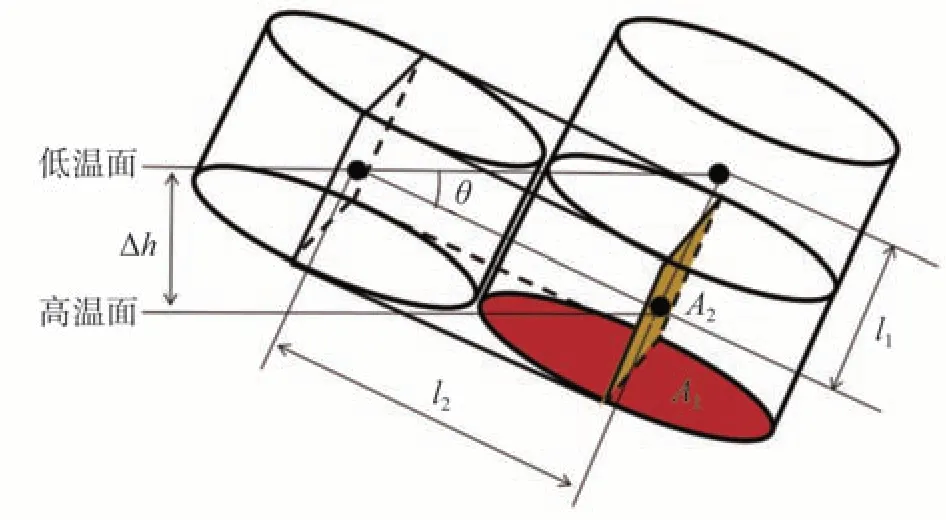
圖19 熱導率計算中物理量的幾何關系

圖中：θ為電樞的扭轉角度；Δh為高溫面和低溫面之間的距離，mm；l1為電樞從高溫面向低溫面傳熱時，熱流在裸銅線中的傳熱路徑長度，mm；l2為疊壓漆包線之間的傳熱路徑長度，mm。其計算公式為

圖中：A1為裸銅線的傳熱面積，mm2；A2為漆包線之間傳熱的等效面積，mm2。其計算公式為

在明確上述物理量的計算方法后，Δh長度的絞合電樞熱阻計算公式為

絞合電樞的熱導率λT的計算公式為

式中AE為電樞樣品的截面積，mm2。

由于上述Rx和λx為漆包線疊壓后各導體之間的未知熱導率，無法直接通過材料性質獲得，因此須通過實驗結果進行求解，并對結果進行分析。通過絞合電樞樣品#3～#9的實驗數據，可以在代入式(19)后解得λx。同時，由于絕大多數車用電機電樞均采用銅線，其物理性質有較好的一致性，所以可以將λx的主要影響因素歸結為加工工藝造成的差異，所以對于具有不同工藝的電樞結構求取平均值計算經驗系數是有意義的，其結果如表6所示。

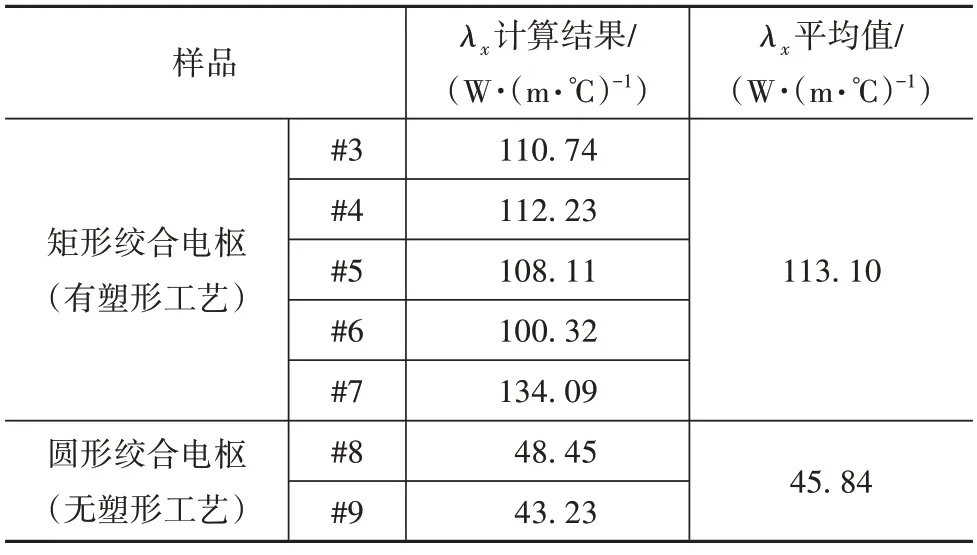
表6 λx計算結果

通過表6 可進一步將絞合電樞分為兩類，其一是具有塑形工藝的矩形絞線，其二是不具有塑形工藝的圓形絞線。計算結果表明，矩形絞線在封裝后之所以在漆包線之間有更好熱導率，其原因在于矩形線在絞合完成后會首先經過一次塑形擠壓，在施加一定預緊力制成電樞后會產生更緊湊的結構，因此封裝工藝對其熱導率的影響也會更顯著。但值得注意的是，該經驗值只能表達浸漬電樞內部微觀的傳熱行為規律，而不能代表電樞整體的截面方向熱導率。

3.3 模型的意義

經過前文對實驗結果的分析，表明封裝工藝對于絞合電樞的熱導率影響非常明顯。同時，對于平行電樞和絞合電樞的數學模型分析也證明了封裝工藝對電樞槽內熱導率的影響權重。

基于式（8）中的計算方法，計算平行電樞樣品#1和#2的軸向熱導率結果如表7所示。

基于式（19）的計算方法與表6 中得出的漆包線內部傳熱經驗系數，計算絞合電樞樣品#3～#9 的軸向熱導率結果如表8所示。

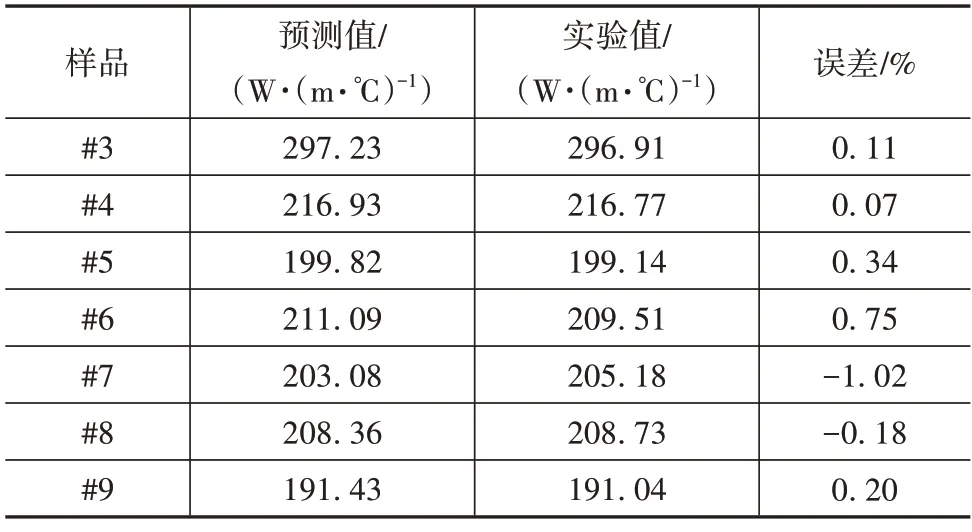
表8 絞合電樞封裝后熱導率預測結果

綜上所述，通過將表6 中的結論代入式（8）與式（19）的數學模型可以得到電樞的軸向熱導率一般估算方法。

平行電樞：

非塑形絞合電樞：

塑形絞合電樞：

上述結論解決了包括發卡繞組、圓形漆包線、換位漆包線、矩形利茲線和圓形利茲線在內的幾乎所有車用電機電樞的軸向熱導率估算問題。上述模型可使電機設計者憑借電樞的結構信息即可計算出電樞在封裝后所表現出的溫度服役行為，有效地簡化了表1 中文獻所使用的等效模型和等效介質理論等數學方法。同時，上述模型的提出可以將絞合電樞軸向熱導率的預測誤差控制在1.1%以內，對于現有文獻中的溫度預測結果也是明顯進步。另一方面，該模型的提出也表明絞合電樞在應用過程中使用塑形工藝能夠有效提升其軸向熱導率這一現象。

4 結論

為滿足各類電動車輛驅動結構的性能要求，多樣化的電樞被應用在驅動電機中。而封裝工藝對各類電樞的影響在車用電機的溫度預測中是不可忽略的重要影響因素。選取9 款有代表性的電樞結構，測量了其封裝后電樞的熱導率，并將其歸納為“平行電樞”和“絞合電樞”兩種結構類型進行建模分析。通過實驗結果與建模分析可知，封裝工藝對包括換位漆包線和利茲線在內的“絞合電樞”的軸向熱導率有明顯提升作用。基于上述性質，本文對兩類電樞分別建立等效熱導率模型，并求解絞合電樞內部疊壓漆包線之間的傳熱效率。計算結果表明，封裝工藝對具有塑形工藝的矩形絞線的熱導率有最顯著的提升作用，圓形絞線次之。最后，通過經驗模型能夠合理地預測各類電樞的軸向熱導率，其計算誤差在1.1%以內。