車載機槍托架行進間發射動力學分析與優化

郁衛星,楊 臻,劉萬川,張夢飛,景春溫

(1.中北大學 機電工程學院,太原 030051;2.重慶建設工業(集團)有限責任公司,重慶 400054)

0 引言

托架是槍座上的主要承力構件,連接車輛和機槍。機槍行進間射擊時,托架既要承受路面不平經車體傳遞的隨機振動,也要承受機槍由于連續發射帶來的后坐沖擊力,導致它的受力情況非常復雜。其結構剛強度對武器系統射擊精度等動態特性影響較大[1]。車載機槍在一些遭遇戰中對中小目標有很好的火力壓制作用,所以對其射擊精度有較高的要求。為改善車載機槍在行進間射擊的穩定性和可靠性,研究托架在隨機路面振動和持續沖擊作用下的力學性能并加以改善至關重要。

戰車行進過程中路面狀況和車速是影響車體振動的主要因素[2-3],車體振動沖擊會經過托架傳遞到車載機槍上,通過改進托架搖架結構布局或增加支撐系統可以有效減小振動沖擊對射擊精度的影響[4-6],同時機槍發射時,后坐沖擊也會對托架的剛度及疲勞壽命產生較大影響[7],所以本文對行進間射擊時的托架進行力學仿真,能有效進行托架的剛強度校核和射擊精度影響分析。并根據仿真結果,采用拓撲優化結合參數化建模方法對托架進行結構優化[8-9],有效提高了車載機槍行進間射擊時的精度和穩定性。

1 基本理論

1.1 路面不平度理論

戰車在作戰時一般行駛于未鋪裝的路面,行進時會受到由于路面起伏引起的隨機振動,導致機槍托架受到隨機的振動激勵[10]。車輛作為傳遞系統將路面不平度激勵輸入到機槍托架上。

將路面相對于基準平面的高度q,沿道路走向長度d的變化q(d)稱為路面不平度,定義其功率譜密度為Gq(n)。按照國家標準GB/T7031—2005機械振動道路路面譜數據,將道路等級分為8級,由于裝甲車、突擊車多為野外作戰,故選擇標準中的D級路面,包括砂石鋪筑的簡易路面及壓實的未鋪裝路面等[10],此時路面不平度位移功率譜密度表示為:

式中:n為空間頻率,m-1;n0為參考空間頻率,取值為0.1 m-1;Gq(n0)為路面不平度系數,由國家路面等級分類給出;w為頻率指數,取值為2。

式中:f為時間頻率,f=un;u為車速[11]。

通過諧波疊加法[12]可以得到路面垂直加速度a隨時間變化圖像如圖1所示。

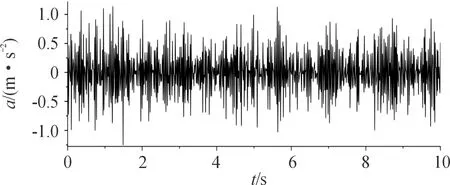
圖1 路面垂直加速度時域曲線

1.2 發射動力學理論

托架除了承受行進間由于路面不平度引起的振動外,在實際作戰時,還會承受由機槍連續射擊引起的后坐沖擊,此沖擊為強沖擊,會對托架的結構剛強度有較大影響。

機槍射擊引起的后坐力主要由彈藥的內彈道過程產生的反作用力引起,根據某12.7 mm機槍射擊過程中的物理化學變化,結合內彈道的基本假設,建立內彈道期間的數學方程,計算得到膛內火藥氣體壓力隨時間變化的情況。

假設機槍在射擊過程中,機槍整體受到的后坐力Ff與膛底壓力Ft相等,即:

Ff=Ft=pS

(4)

式中:p為膛內平均壓力;S為膛底截面積。

在機槍連續射擊時,后坐力隨彈丸擊發而重復,設機槍射頻為600發/min,則當機槍連續射擊10發時,后坐力變化曲線如圖2所示。

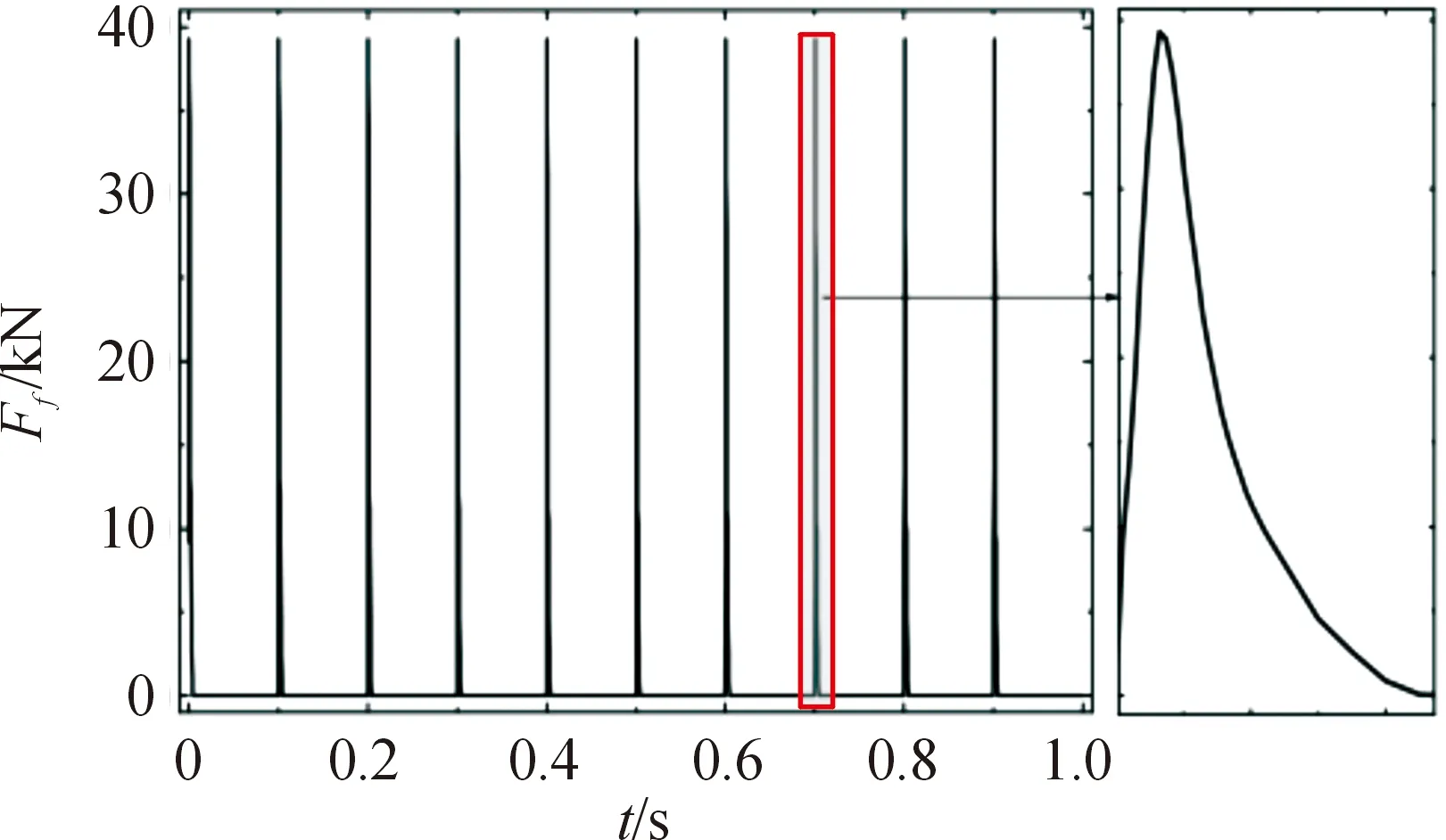
圖2 10發連射后坐力曲線

2 行進間發射模型

行進間發射動力學模型是為了分析車載武器在路面不平度輸入以及射擊載荷同時作用下的動力學響應[13],分析時,將整個車載機槍系統簡化為車輛和機槍2個部分,2個部分由托架連接,托架模型簡圖如圖3所示。

圖3 托架示意圖

車輛系統由輪胎、懸架、車體框架等結構組成,由于托架固有頻率遠離輪胎等結構的固有頻率,在進行車輛垂直振動分析時,將車輛系統簡化成單自由度振動系統。

機槍系統由多個零部件及運動機構組成,內含機框、身管、機匣、槍托、槍管簧、復進簧等彈性構件,運動情況復雜;為了簡化模型并放大工況,將整個機槍發射系統簡化為一個質量為18.5 kg的槍體,槍體后坐力主要來自膛底氣壓對內膛截面的作用力。機槍與托架之間有緩沖裝置,裝有緩沖裝置的滑板底座固連于托架上,緩沖裝置另一端直接連接槍體。簡化后的行進間發射模型如圖4所示。

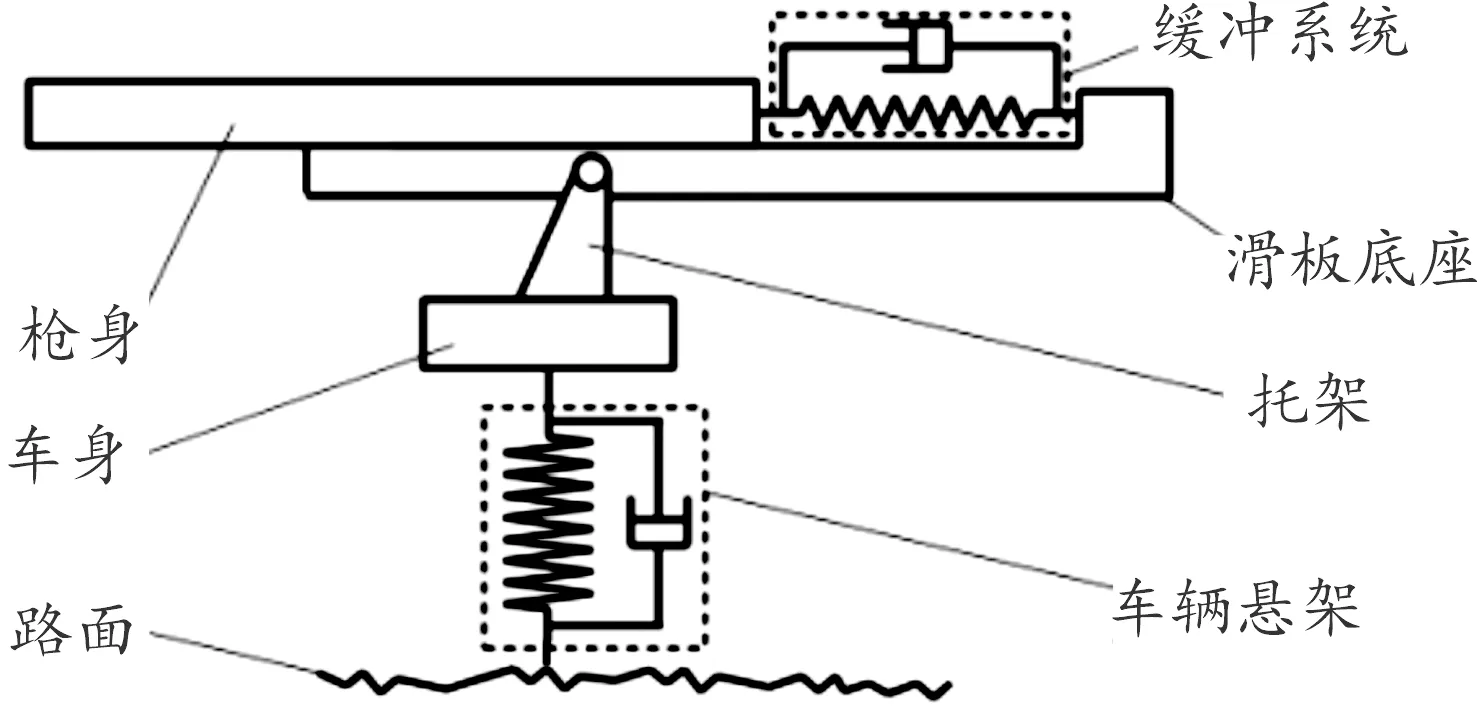
圖4 行進間發射模型圖

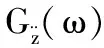
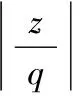
式中:ζ為系統的阻尼比,取0.25;λ為頻率比。

最終得到車輛系統的加速度輸出,即托架受到的加速度激勵的功率譜密度曲線如圖5所示。

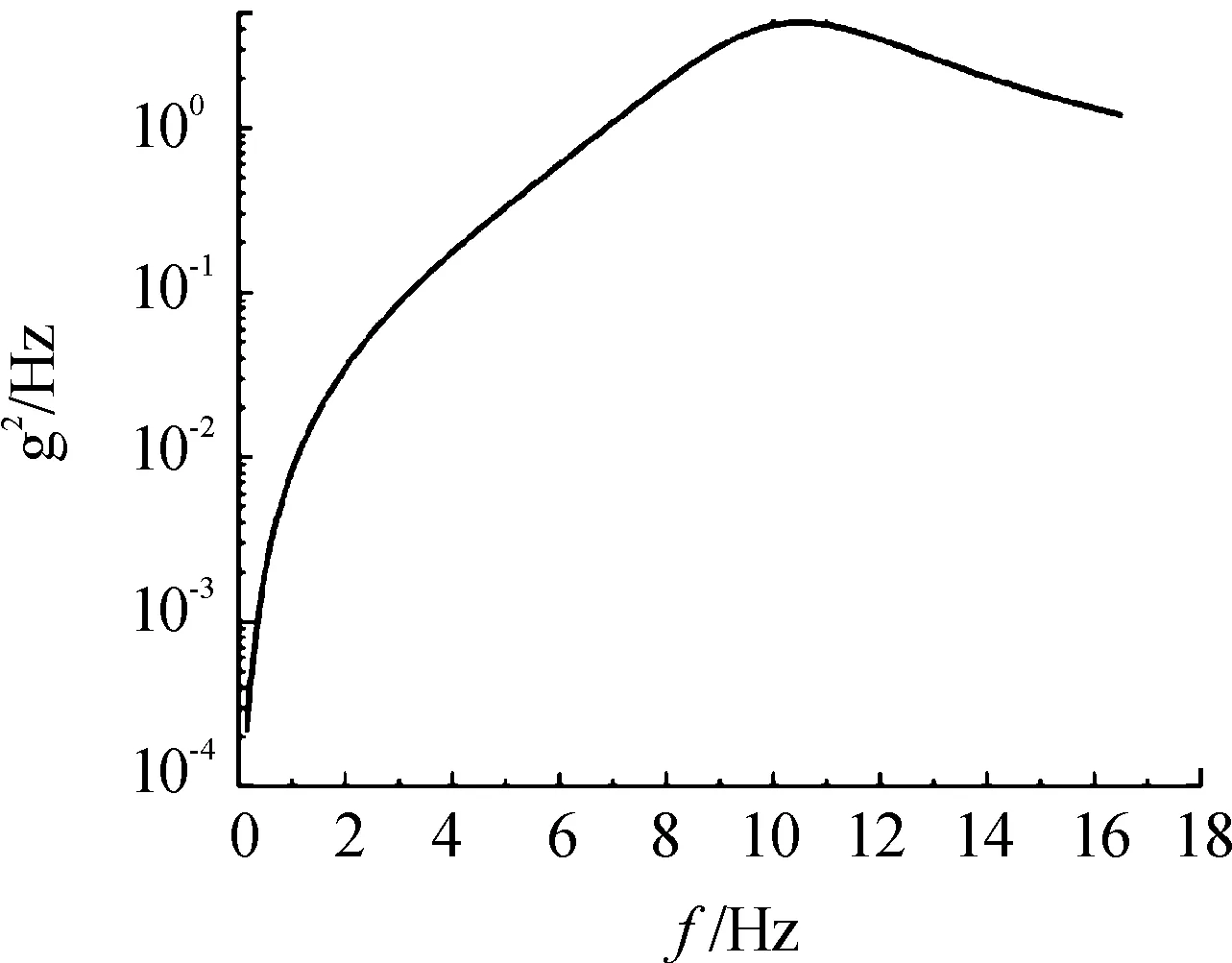
圖5 PSD曲線

對于機槍,取滑板為慣性參考系,可以得到系統的運動微分方程為:

式中:F為滑板受到的后坐力;m為槍身質量;c、k分別為緩沖系統的彈性系數和阻尼系數;x為槍身位移。

將槍身在10發連射時的后坐沖擊Ff作為輸入,得到了滑板(即托架)受到的沖擊力曲線如圖6所示。

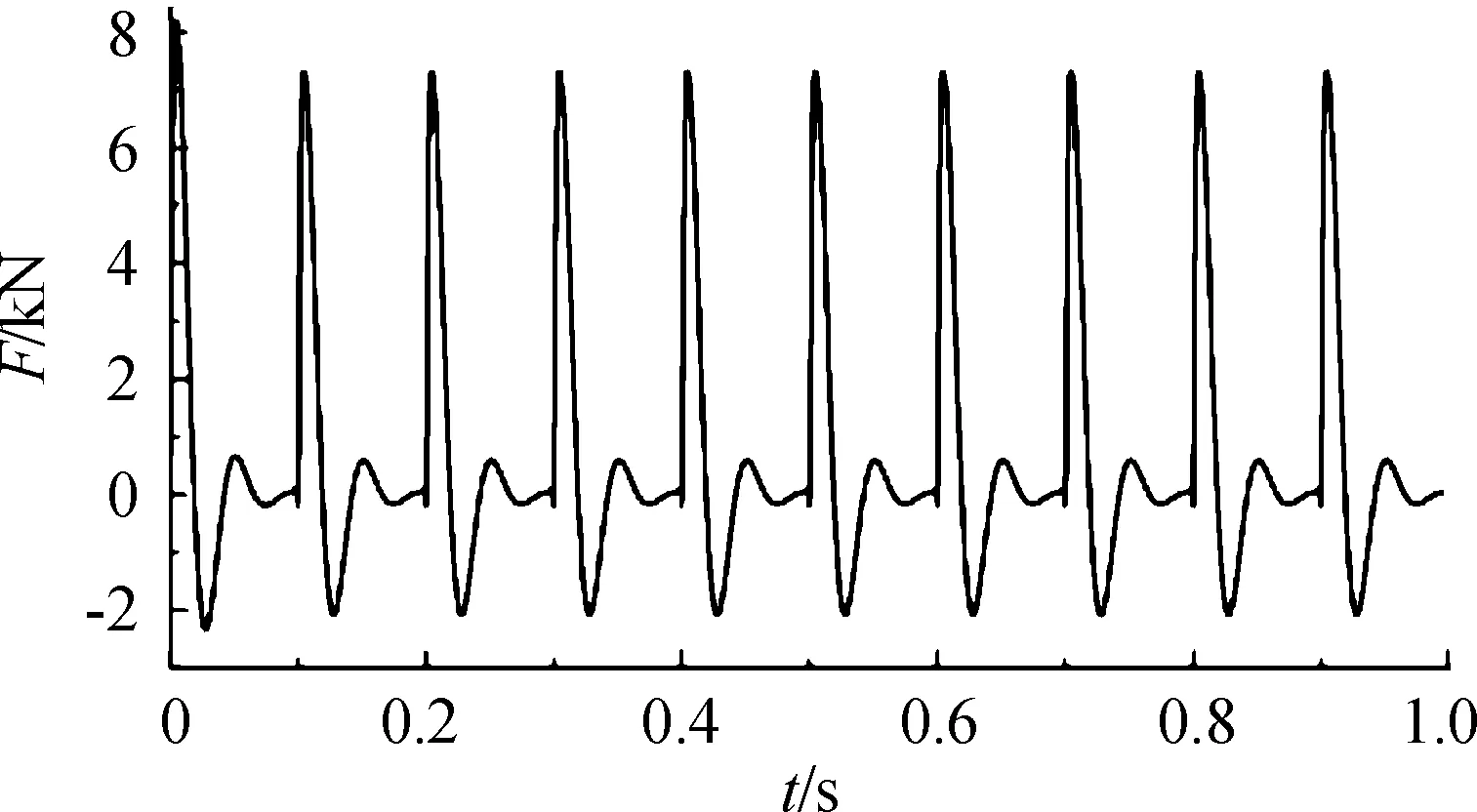
圖6 滑塊后坐力曲線

唐俊智[14]在某遙控武器站結構設計時,將車載機槍架座安裝在固定平臺上,進行3～5發點射,實驗得到固定槍架上的后坐力為8 000 N;由圖6可知,數值模擬出現最大后坐沖擊力為8 194 N,與實驗數據差別不大,故數值模擬的數據具有可靠性。

3 仿真分析

3.1 假設

在對托架進行仿真分析時,做出如下假設:

1) 機槍與托架之間的滑板為剛體,在射擊時不會產生變形。

2) 托架與車輛之間為剛性連接,車輛的振動響應直接作用于機槍。

3) 高低機的大小齒弧均為剛體,且二者完全嚙合,能夠完全傳遞力。

4) 機槍質心與托架耳軸連線與身管平行。

此時,以托架耳軸中心為原點,建立oxy坐標系,x軸正向指向槍口方向,y軸向上為正,對托架的受力分析如圖7所示。

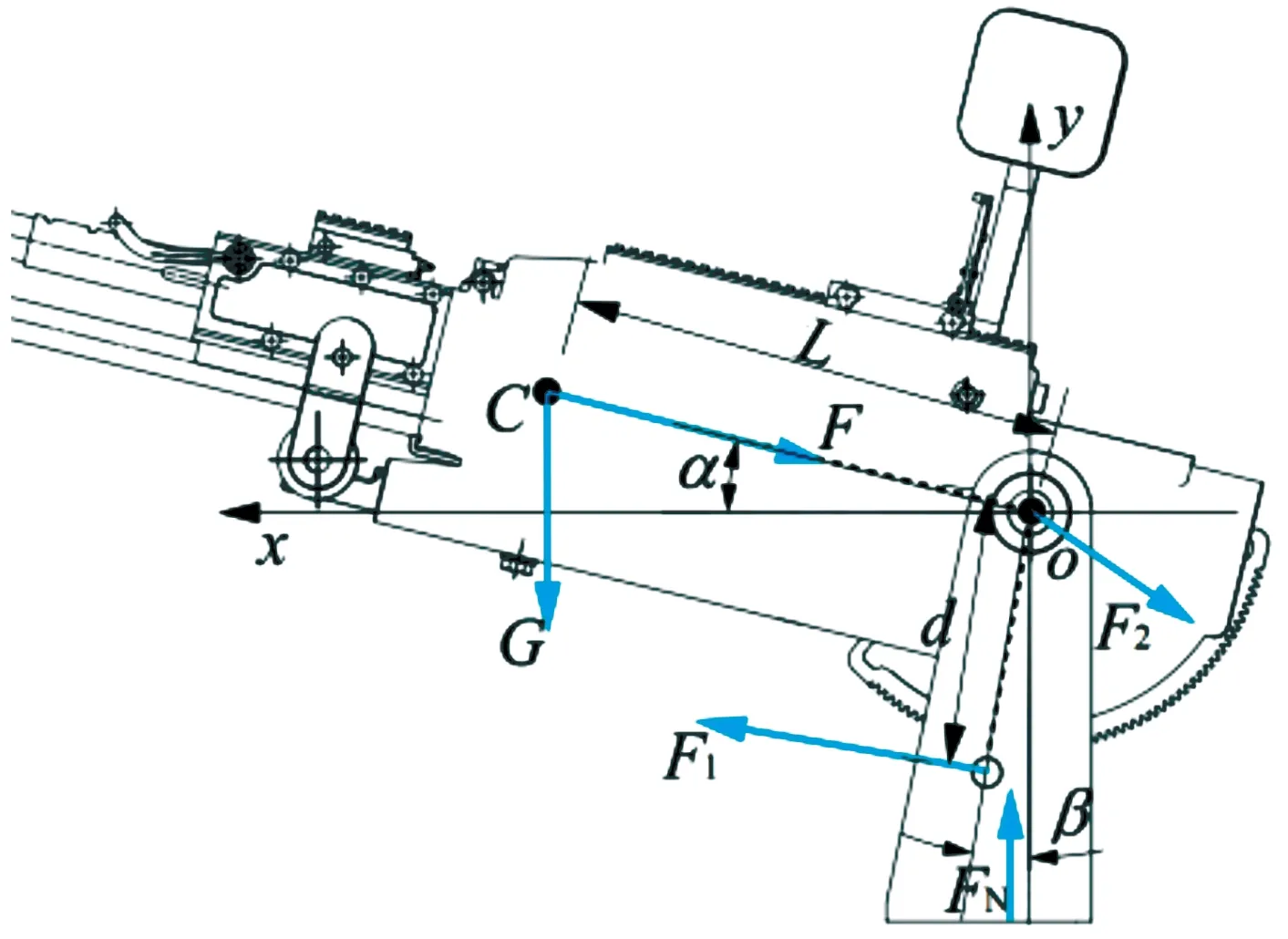
圖7 受力分析圖

圖7中,α為托架耳軸中心與機槍質心連線與x軸夾角;β為高低機兩齒輪中心連線與y軸的夾角;L為機槍質心C與耳軸中心o的距離;d為高低機兩齒輪中心距;G為槍身和滑板的等效質量;F為后坐沖擊力;F1為高低機手輪與托架之間的作用力;F2為機槍對托架的壓力;FN為車輛對托架的支持力。

由圖7可得:

式中:m為托架質量,值為9.86 kg;M為系統總質量,值為34 kg;a(t)托架車輛輸出的加速度;g為重力加速度,取值 9.8 m/s2。

3.2 力學仿真

在ANSYS仿真軟件中,對托架進行受力仿真分析,得到在3種射角下10發連射過程中托架應力σ、變形δ隨時間的變化曲線如圖8、圖9所示。

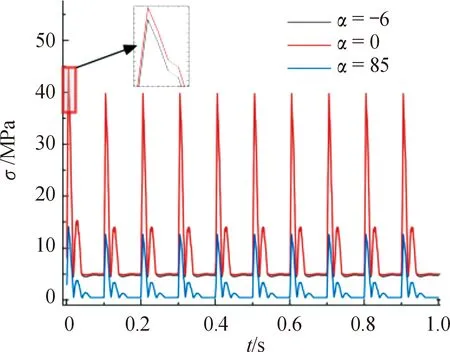
圖8 應力變化曲線

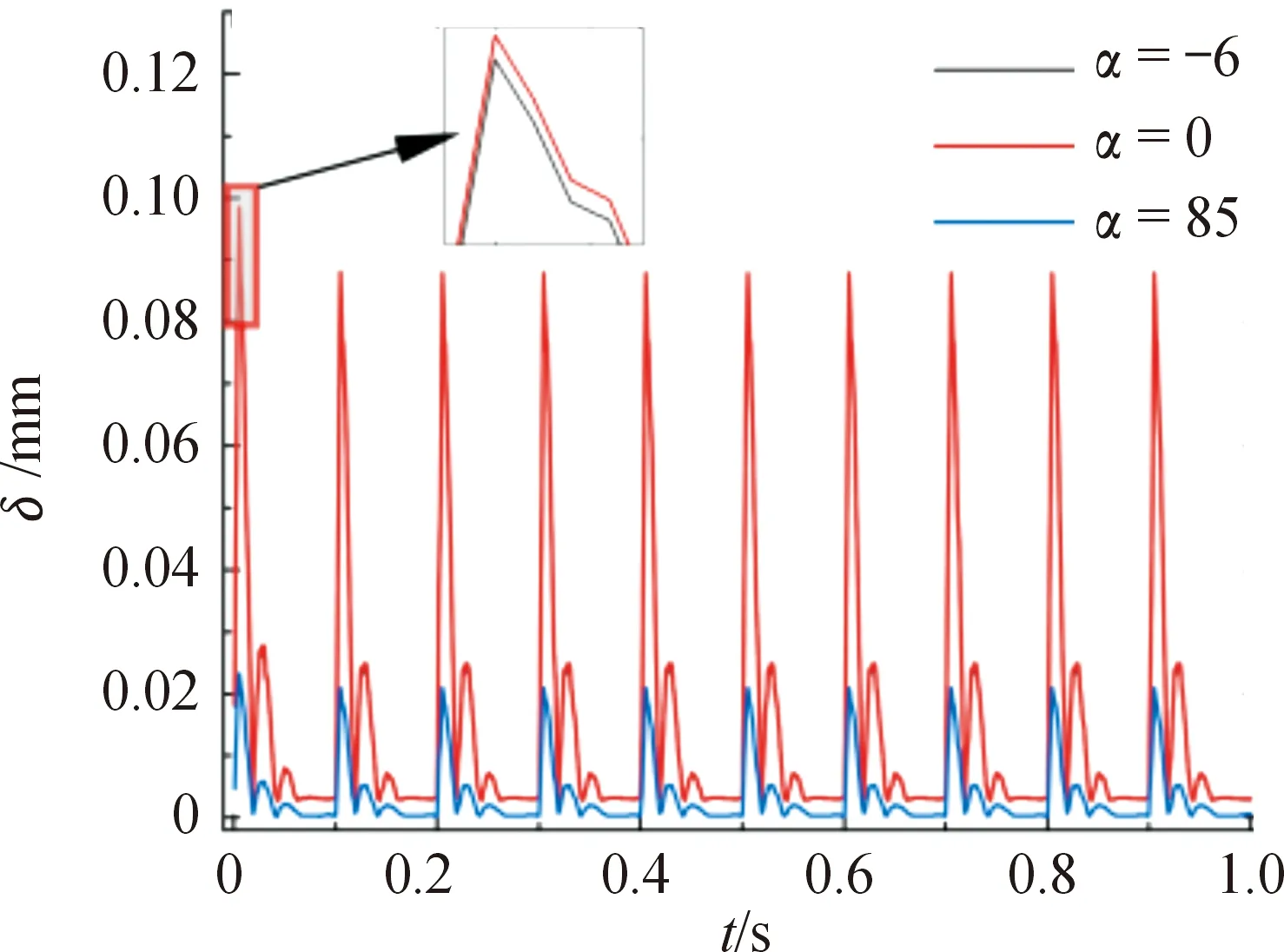
圖9 變形變化曲線

由圖8、圖9可知,射角為-6°和0°時的應力和變形基本一致,射角為85°時的應力和變形相對較小,應力及變形的變化規律與機槍后坐力變化情況相似,所以托架變形主要受到的是機槍后座力的影響。最大應力及變形結果如表1所示。

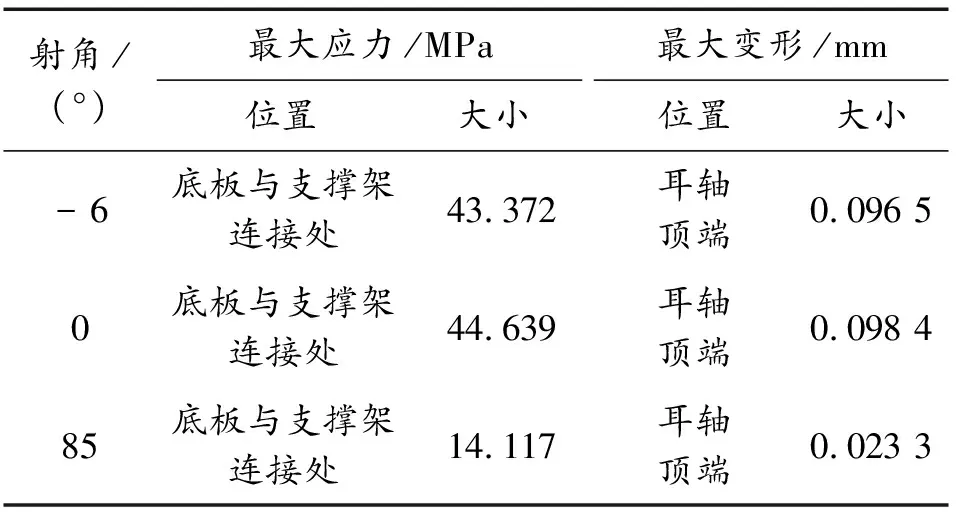
表1 最大應力變形

材料選用結構鋼,其屈服強度σs為235 MPa,由于托架本體最小安全系數為2[15],故許用應力[σ]取117.5 MPa。由表1知,在機槍射擊10發的過程中,滿足剛強度要求。3種射角對比下,平射時托架工況最為惡劣,此時的最大應力、變形云圖如圖10、圖11所示。

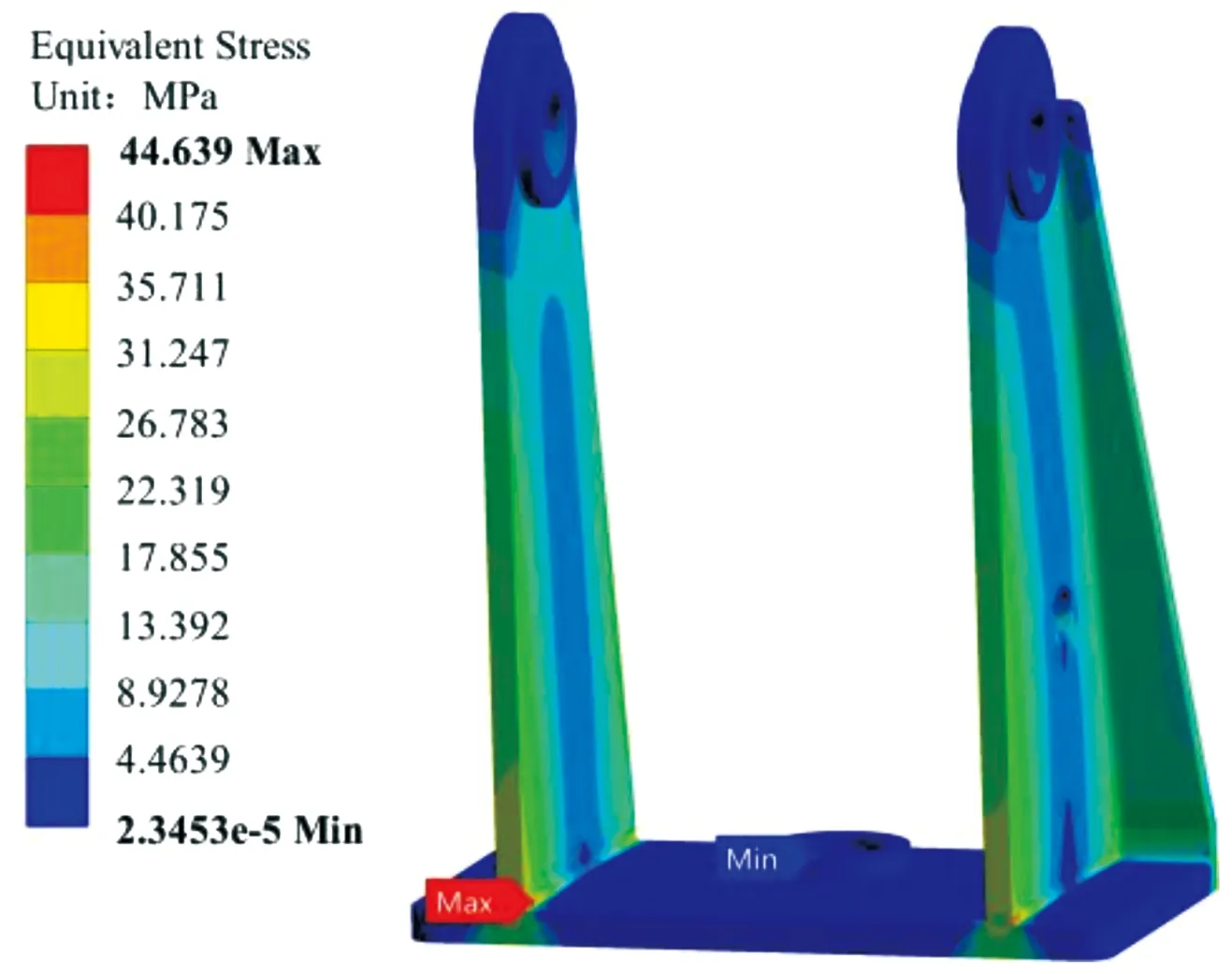
圖10 應力分布云圖

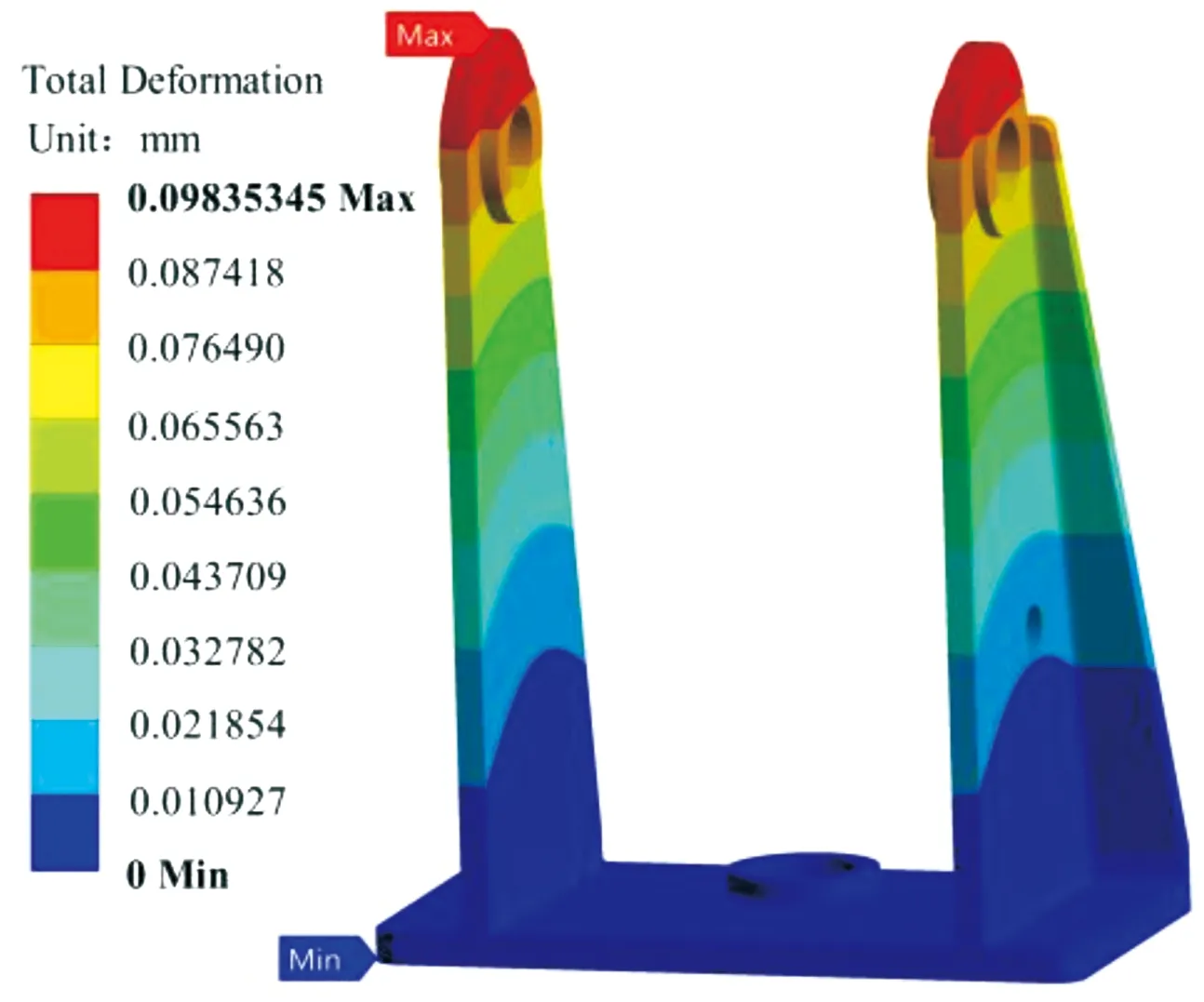
圖11 變形分布云圖

由圖10、圖11可知,在機槍平射10發的過程中應力最大點出現在托架底板與支撐架連接處,該部位是保證結構可靠性的關鍵部位。該部位出現的最大應力不超過44.639 MPa,離許用應力差距較大,在持續射擊下不會出現低周疲勞,滿足使用要求。

最大變形出現在耳軸頂端,耳軸直接與機槍相連接,由于高低機的存在,兩邊耳軸的變形并不對稱,兩耳軸會產生一個交錯變形,該變形會使機槍產生水平方向上的偏角θ,從而引起射擊誤差。托架變形示意圖如圖12所示。

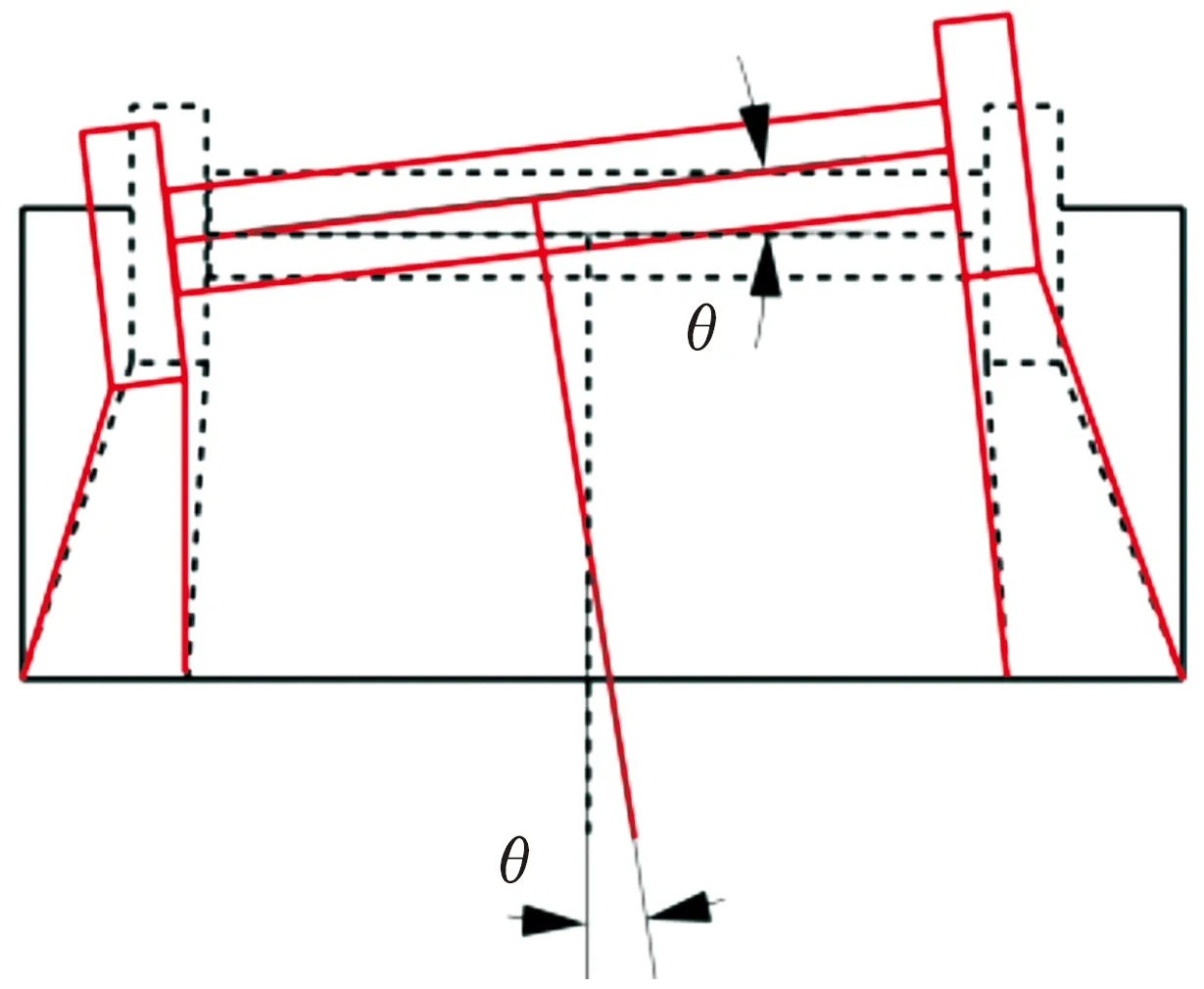
圖12 托架變形示意圖

式中:δ1,δ2分別為托架兩支撐板的最大變形量;l為兩耳軸之間的距離。

由ANSYS變形結果可以得到行進間10發連射時由托架變形引起的槍口偏角曲線如圖13所示。

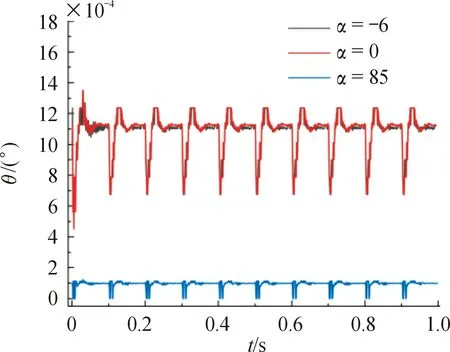
圖13 槍口偏角變化曲線

以有效射程為1 500 m計算,可計算得到3種工況下的最大槍口偏角和目標位置的射擊誤差Δ如表2所示。

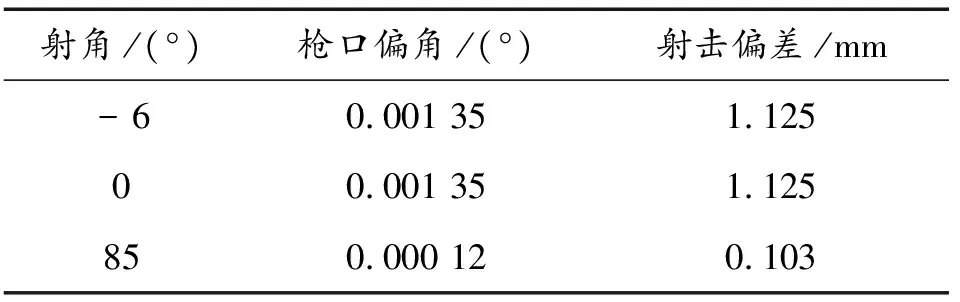
表2 最大射擊誤差表

由圖13可知,平射與射角為-6°時,槍口偏角相對較大,變化情況基本一致,射角為85°時偏角最小;槍口存在最大偏角為0.001 35°,出現時間為一次擊發完成后,但是由于槍身自重和車身垂直加速度的存在,槍口在彈丸離槍后會一直有一個0.001 11°的偏角;因為將槍體視為剛體,所以槍口偏移量主要是由于偏角的存在而形成的,其變化趨勢與槍口偏角一致,最大偏移量為0.011 3 mm。

4 結構優化設計

由仿真結果云圖可知托架部分結構的應力很小,存在較大冗余量,可以通過拓撲優化的方法對這部分結構進行重新設計。拓撲優化就是在給定的設計域里面,尋找到滿足邊界約束的最優結構分布[16],此處運用ANSYS Workbench的拓撲優化模塊進行優化設計,該模塊基于變密度法對托架結構進行優化。

變密度拓撲優化方法是基于有限元方法的一種結構優化方法,在有限元方法的基礎上,將每個離散的單元定義為獨立變量,該變量記為單元的相對密度,即偽密度設計變量。偽密度為0(或接近0)表示對應的單元處無實體,去除該部分材料;偽密度為1(或接近1)則表示對應的單元處為實體,保留該處的材料[17-18]。

變密度法通過偽密度的變化控制單元剛度的變化,進而調整結構總體剛度矩陣的變化,在給定約束下進行計算,經過優化使托架的結構剛度達到最佳,材料分布達到最優[19]。

本文中將2塊支撐板作為設計域進行拓撲優化,為了保證托架在任意工況下都能滿足強度使用要求,選取平射作為仿真工況,并取取安全系數為2[15],故許用應力[σ]取117.5 MPa,為了減少構冗余質量,保留60%的質量。經過28次迭代計算后得到圖14(a)所示的拓撲優化構型,根據優化結果進行部分結構重新設計,保留主傳力路徑,對較厚的支撐板進行減厚處理,去除冗余質量。

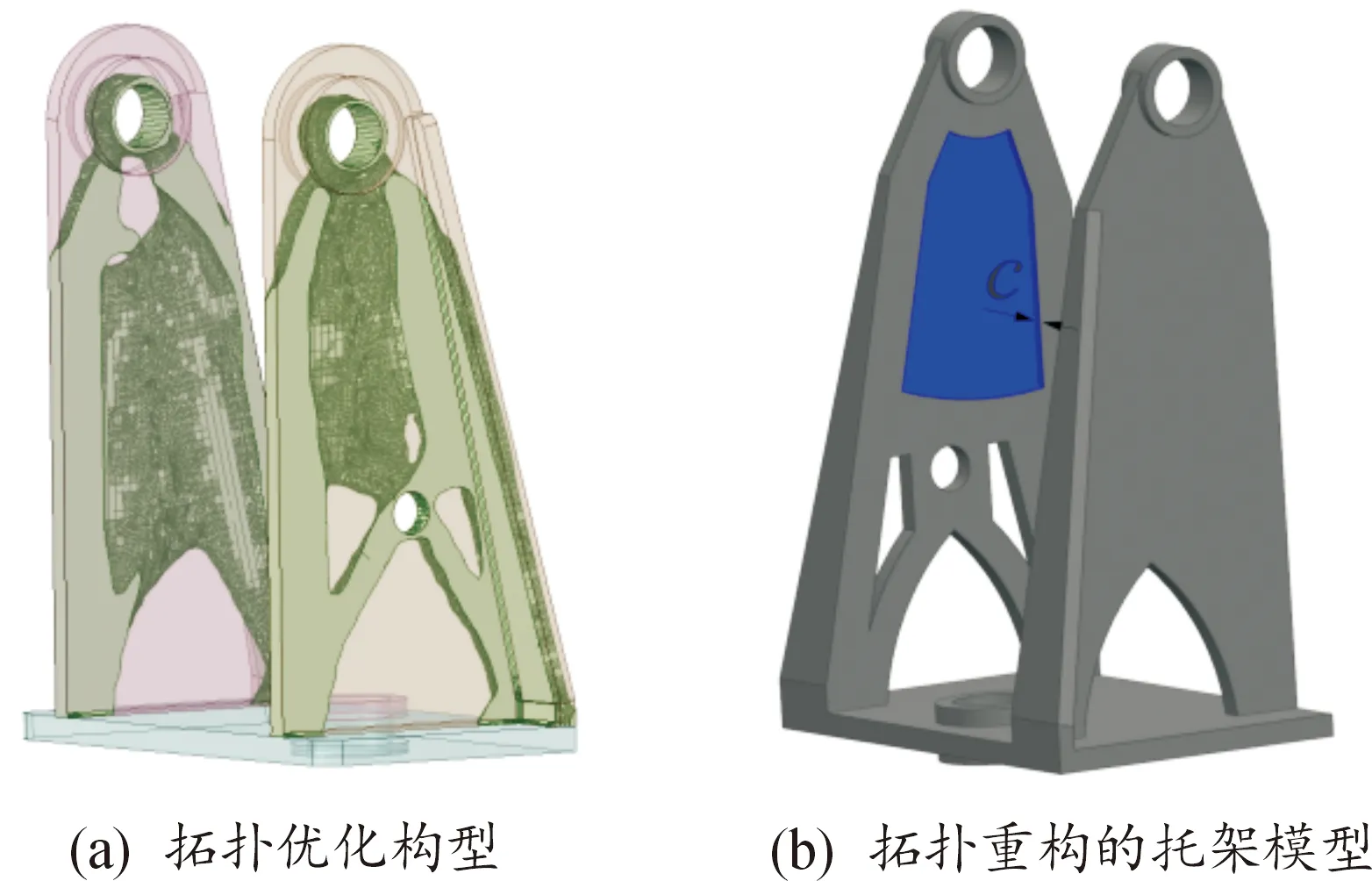
圖14 結構優化簡圖Fig.14 Structure optimization brief diagram

由于高低機及平衡機的存在,使得2支撐板受力并不對稱,導致兩耳軸在連續發射過程中會產生交錯變形,形成射擊偏差。為減少該交錯變形,需要對2支撐板進行分別設計,保證行進間射擊工況下的剛度匹配,減小這部分射擊偏差。

在拓撲重構的托架模型基礎上,為了實現對2支撐板剛度進行分別控制、提高仿真運算效率,以右支撐板減去部分(圖14(b)深色部分)的深度c作為設計變量,使用UG聯合ANSYS Workbench進行參數化建模仿真[19]。在UG建模時定義拉伸深度為變量,其值定義范圍為[2,4],以平射工況作為對比條件,對比不同深度的力學性能響應,得到托架力學性能變化曲線如圖15所示。

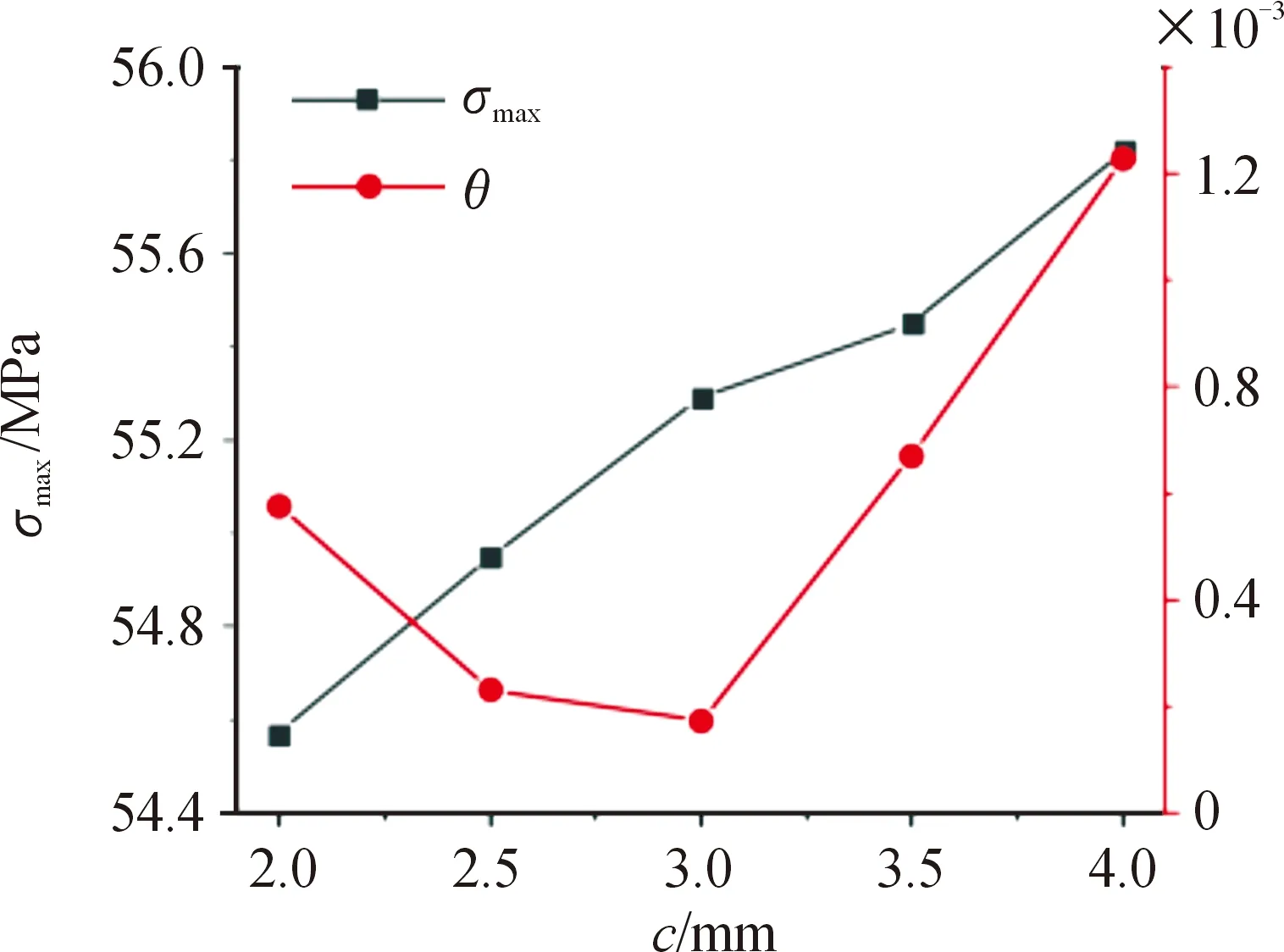
圖15 力學性能變化曲線

由圖15可知,當減去深度為3 mm時,優化效果最好,以此作為最終優化結構,得到相關參數如表3所示。

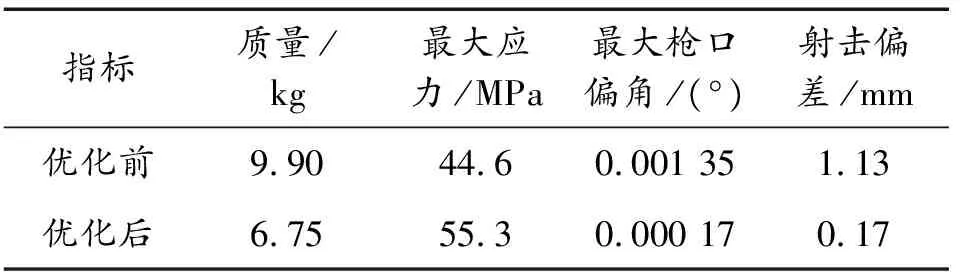
表3 優化前后參數對比

由表3可知,優化托架結構后,托架質量降低了31.82%;支撐板剛度匹配性得到改善,由托架變形引起的射擊偏差減小至0.17mm,對射擊基本沒有影響,最大應力較原結構有一定幅度的上升,但遠小于許用應力,不存在低周疲勞及強度失效的情況,依然滿足強度條件。

托架經過優化后,極大降低結構質量,在滿足使用強度要求的同時,還能夠有效提高托架支撐板的剛度匹配性,從而減小行進間射擊時由托架變形導致的射擊偏差。優化后托架的結構變形,基本不會影響機槍正常工作。

5 結論

本文通過建立行進間發射動力學模型,得到托架的受力情況,對托架進行有限元仿真,得到3種工況下托架的力學性能和對機槍射擊精度的影響,通過拓撲分析優化,對托架的支撐板進行重新設計,利用參數化建模的方法,提高2支撐板的剛度匹配性,使支撐板的交錯變形得到有效控制,從而減小射擊偏差。主要結論如下:

1) 在2種激勵同時作用下,平射時的工況最為惡劣;托架所受到的最大應力位于底板與支撐架連接處,大小為44.639 MPa,遠小于許用應力,滿足強度要求;最大變形量為0.098 4 mm在材料的彈性變形范圍內,滿足剛度要求。

2) 最大應力的變化規律與機槍后坐力變化情況相似,即機槍的后坐沖擊為托架所受力的主要部分。

3) 通過拓撲優化結合參數建模仿真分析的方法對托架進行結構重新設計,減小托架在行進間射擊過程中的交錯變形。結構優化后,滿足結構強度的同時,結構質量減小31.82%,托架耳軸變形最大會引起槍口會產生0.000 17°的槍口偏角;換算到目標位置,最大會產生0.17 mm的射擊偏差;優化后的托架變形引起的射擊誤差,基本不會影響機槍正常工作,可以為車載機槍及遙控武器戰設計提供有效參考。