基于改進型CEEMDAN-Stacking集成學習的短期電力負荷預測

李 翔，沈艷霞

（江南大學 物聯網技術應用教育部工程研究中心，江蘇 無錫 214122）

0 引 言

電力負荷預測作為電力系統部門的一項重要工作，對保證電力系統的合理規劃與調度、提高經濟效益具有十分重要的意義[1]。準確的電力負荷預測能夠為電網規劃提供更好的指導，有利于電力系統的安全穩定運行，使電能得到更充分的利用。

電力負荷預測中，傳統的時間序列模型（如自回歸滑動平均模型、Prophet、馬爾科夫鏈等）對于數據波動性不大、平穩性較好的序列具有較好的預測效果，但是難以捕捉非平穩序列中復雜的時間依賴關系。人工智能領域的機器學習和深度學習算法也被廣泛應用于負荷預測，常見的預測模型有支持向量機、極限學習機、長短期記憶（Long Short-Term Memory，LSTM）神經網絡等[2,3]。文獻[4]按照重要程度對輸入特征進行篩選，并使用貝葉斯優化的極限梯度提升（eXtreme Gradient Boosting，XGBoost）模型進行負荷預測。文獻[5]對原始負荷數據進行經驗模態分解，建立了基于注意力機制的門控循環單元網絡并對各分量預測，將各預測值疊加形成最終的預測值。通過對原始序列進行分解處理，降低了原始序列的非平穩定性和復雜性。此外，對分解后的子序列進行建模預測，有效提高了模型的預測精度。然而，單一模型難以全面挖掘數據之間的變化規律，也限制了模型的泛化性。文獻[6]基于特征選擇的方式，采用Stacking集成學習融合多種算法進行負荷預測。文獻[7]通過Stacking 算法融合多層門控循環單元網絡實現風電功率預測。文獻[8]利用改進的螢火蟲算法優化核嶺回歸模型中的參數，通過Stacking 算法融合各核嶺回歸模型對風速序列進行預測。集成學習方式可以結合多個模型的優勢，整體提升了模型的預測性能。

由于以上文獻均采用傳統的Stacking 模型，忽略了基學習器在交叉驗證時所形成的不同模型之間的差異性，影響了模型的預測精度。文獻[7]和文獻[8]均使用了Stacking 進行建模，但并沒有對原始序列進行分解處理，仍未降低序列的非平穩性和復雜性。基于此，對滑動窗口處理后的負荷序列進行自適應噪聲完備集合經驗模態分解（Complete Ensemble Empirical Mode Decomposition with Adaptive Noise，CEEMDAN），并重構其模態分量[9]。根據Stacking 集成學習模型中不同學習器的預測精度，對其在測試集上的預測結果分配權重，利用改進的Stacking 模型融合LSTM神經網絡、XGBoost、K 最鄰近（K-Nearest Neighbor，KNN）模型以及多層感知機（Multilayer Perceptron，MLP）實現短期電力負荷預測。

1 基于滑動窗口的CEEMDAN 分解與重構

1.1 滑動窗口處理

考慮到電力負荷數據較強的時序關聯性，對數據集中的負荷數據按滑動窗口方式進行處理（見圖1），將特征負荷序列x(i)和目標負荷序列y(i)分別作為模型的輸入和輸出。其中，x(i)表示過去i天的歷史負荷序列，y(i)表示第i+1 天的負荷序列。

圖1 滑動窗口處理方式

1.2 CEEMDAN 分解

對滑動窗口處理后的電力負荷序列進行CEEMDAN 分解，分解算法的步驟如下。

（1）設原始電力負荷序列為x(t)，第i次添加高斯白噪聲后，新的電力負荷序列xi(t)為

式中：εk為第k個信噪比；ωi(t)為第i次加入的高斯白噪聲序列。

（2）對xi(t)進行經驗模態費解（Empirical Mode Decomposition，EMD），得到第1 個模態分量IMF1(t)和第1 個剩余分量r1(t)為

（3）對新的信號r1(t)+ε1E1[ωi(t)]進行EMD 分解，得到第2 個模態分量IMF2(t)為

式中：E1(·)為EMD 分解產生的第1 個模態分量的算子。

（4）重復步驟（3）的計算過程，得到第k+1個模態分量和剩余分量。

（5）當達到EMD 的停止條件時，分解結束，原始電力負荷序列被分解為若干個模態分量和1 個剩余分量。為了適應后續的預測模型，將需要得到的IMF 數量作為CEEMDAN 分解結束的停止條件[10]。

1.3 模態分量重構

為了降低模型在時間和計算上的復雜度，將各模態分量重構為高頻分量和低頻分量。假設電力負荷序列經過CEEMDAN 分解成m個不同的內涵模態分量（Intrinsic Mode Functions，IMF），本文將前m-1個分量重構為高頻分量H，第m個分量為低頻分量L，重構方式為

由于重構得到的高頻序列和低頻序列中負荷數據的傳輸方式相同，為了方便描述，將特征負荷序列用Xi表示，將目標負荷序列用Yj表示，其中Xi=(xi,xi+1,…,xi+N-1)，則輸入向量分別為(x1,x2,…,xN),(x2,x3,…,xN+1),(xn,xn+1,…,xn+N-1)，對應的標簽分別為(YN+1,YN+2,…,Yn+N)。

2 負荷預測模型

2.1 Stacking 集成學習框架

Stacking 集成學習框架通過對多種不同算法的融合，從整體上提升模型的性能。Stacking 框架由2 層學習器構建而成。第1 層中包含多個基學習器，第2層中包含1 個元學習器，如圖2 所示。

圖2 Stacking 集成學習框架

首先，將劃分后的數據集輸入第1 層的基學習器中，各基學習器分別預測并輸出其預測值；其次，將輸出的預測值及其對應的標簽作為新數據集，以此訓練第2 層的元學習器；最后，由元學習器輸出最終預測值。

2.2 學習器選擇

Stacking 框架中，第1 層基學習器采用LSTM、XGBoost 以及KNN。LSTM 網絡可以很好地學習序列中的時間依賴關系，在時間序列建模上有一定的優勢。KNN 算法訓練時間快，算法復雜度較低。XGBoost 對上一步預測的殘差進行擬合，可使模型訓練更加充分。第2 層元學習器采用MLP，利用神經網絡進一步擬合預測值和原數據集標簽，從整體上提升模型的預測能力。

2.2.1 LSTM

LSTM 網絡解決了循環神經網絡（Recurrent Neural Network，RNN）中存在的梯度消失和爆炸問題，通過隱藏層不斷地將上一時刻的信息傳遞至下一時刻，同時結合當前時刻的輸入得到對應輸出。設置本文模型中基學習器LSTM 的輸入向量為Xi，輸出向量為。

2.2.2 XGBoost

XGBoost 模型不同于大多數回歸模型采用原始數據進行擬合，而是通過擬合上一步預測的殘差不斷逼近真實值，從而逐步提升模型的精度。

XGBoost 模型的預測值可以表示為

式中：表示預測值；K表示模型所用樹的數量。

XGBoost 模型的目標函數為

目標函數中第1 項表示預測值y^i 和真實值yi的誤差，第2 項表示所有樹的復雜度之和。通過最小化目標函數的方式完成對函數集fk(x)的學習，最后通過累加K棵樹的預測值實現負荷預測。設置本文模型中基學習器XGBOOST 的輸入向量為Xi，輸出向量為。

2.2.3 KNN

KNN 回歸是一種監督學習算法，通過搜索歷史樣本中與預測樣本最接近的K個樣本，并根據平均屬性值進行負荷預測。設置本文模型中基學習器KNN 的輸入向量為Xi，輸出向量為。

2.2.4 MLP

MLP 是一種全連接神經網絡。數據由輸入層傳入隱藏層后，隱藏層中的神經元對數據進行分析和運算，并將結果傳至輸出層，由輸出層對其處理后得到最終的輸出。假設MLP 輸入向量為X，經過運算得到

式中：W1、W2為權重；b1、b2為偏置。

第2 層學習器通過擬合訓練集的預測值與其對應的真實值來訓練MLP 模型，將測試集的預測值輸入訓練好的MLP 中，從而得到最終的預測值。

2.3 CEEMDAN-Stacking 模型中的數據傳輸

在CEEMDAN-Stacking 模型中，電力負荷數據的傳輸方式具體如下。

（1）經過CEEMDAN 分解與模態重構后，數據以滑動窗口的形式傳入模型，輸入為Xi，輸出為Yj。將數據按一定的比例劃分為訓練集和測試集，分別記作Dtrain和Dtest。

（2）將訓練集Dtrain劃分為k份，對于每一個基學習器（以LSTM 為例），將其中的k-1 份合并為訓練集，另1 份作為驗證集。在k輪訓練中均采用k-1組數據訓練LSTM，再用訓練好的LSTM 對驗證集中的特征負荷序列Xi進行預測，輸出對應的預測值，將其構成的集合記為M1。同理，將基學習器XGBoost 的預測值構成的集合記為M2，將基學習器KNN 的預測值構成的集合記為M3。（3）在每個基學習器中（以LSTM 為例），對于測試集中每個樣本的特征負荷序列Xi，采用訓練好的LSTM 模型進行預測，得到k個預測值,yi,2,…,yi,k。對預測值取平均得到=(yi,1+yi,2+…+yi,k)/k，將預測值構成的集合記為N。同理，將基學習器XGBoost 和KNN 的預測值構成的集合分別記為N2、N3。

（4）將上述M1、M2、M3組合成新的訓練集M，將N1、N2、N3組合成新的測試集N。利用新訓練集M訓練元學習器MLP，基于訓練完成后的MLP 模型對新測試集N進行預測，分別得到高頻分量和低頻分量的預測值，最后將二者的預測值疊加形成最終的預測值。

第1 層基學習器中以LSTM 為例，其他基學習器預測方式與LSTM 相同，Stacking 模型結構如圖3、圖4 所示。

圖3 Stacking 第1 層結構

圖4 Stacking 第2 層結構

2.4 Stacking 模型的改進方式

傳統Stacking 模型通過取平均的方式得到測試集的預測結果，忽視了各模型之間不同的預測效果，沒有將預測效果好的模型凸顯出來，同時預測效果差的模型也同等程度地參與其中。此時，應該賦予預測效果好的模型更大的權重，同時削弱預測效果差的模型帶來的影響。改進傳統Stacking 模型中對測試集的預測值取平均的方式，具體的權重分配機制如下。

（1）在訓練集中記錄預測值和真實值Ytrue的平均相對誤差（Mean Absolute Percentage Error，MAPE），分別記作MAPE1,MAPE2,…,MAPEk，計算

（2）根據k個不同模型的預測效果確定對應的權重α(q=1,2,…,k)，則

（3）輸出測試集中各樣本最終的預測值=α1yi,1+α2yi,2+…+αkyi,k。

（4）對其他基學習器采用同樣的改進方式，綜合計算后得到測試集的最終預測值。

以基學習器LSTM 為例，改進Stacking 模型中的權重分配機制如圖5 所示，其他基學習器與之相同。

圖5 改進Stacking 模型中的權重分配機制

2.5 短期電力負荷預測

短期電力負荷預測流程如圖6 所示。

圖6 短期電力負荷預測流程

（1）將原始電力負荷序列按滑動窗口的方式處理，分成若干段特征負荷序列和目標負荷序列。

（2）對滑動窗口處理后的負荷序列進行CEEMDAN 分解，將分解后的各分量重構為高頻分量和低頻分量。

（3）將重構后的高頻分量和低頻分量均采用改進Stacking 模型進行預測，得到高頻分量和低頻分量的預測值。

（4）疊加高頻分量和低頻分量的預測結果，得到最終的電力負荷預測結果。

3 算例分析

3.1 數據集預處理及預測評價指標

數據集采用EMC 公司提供的電力負荷數據集，電力負荷數據顆粒度為30 min，即一天包含48 個電力負荷數據點。本實驗將2020 年2 月1 日—2021 年8 月31 日的數據作為訓練集，2021 年9 月1 日—10月31 日的數據作為驗證集，2021 年11 月1 日—11月30 日的數據作為測試集，利用過去7 天的數據預測未來1 天的電力負荷。為了便于后續模型的訓練，對數據進行歸一化處理，歸一化公式為

式中：xnew為歸一化后的數據；xmax為數據中的最大值；xmin為數據中的最小值。

采用均方根誤差（Root Mean Squared Error，RMSE）、 平均絕對誤差（Mean Absolute Error，MAE）、MAPE 來評價模型誤差，即

式中：yi表示i時刻的實際值；表示i時刻的預測值。

3.2 負荷序列的CEEMDAN 分解與重構

對滑動窗口處理后的負荷序列進行CEEMDAN分解，發現當分解層數為5 時，CEEMDAN 分解取得不錯的效果。通過CEEMDAN 分解后的各模態分量表現出較好的平穩性，各個模態之間差異明顯且無模態混疊現象。隨機選取其中一段序列，分解結果如圖7 所示。實驗中將前4 個分量重構為高頻分量H，后1 個分量為低頻分量L，采用最終的預測模型對重構后的各分量進行預測。

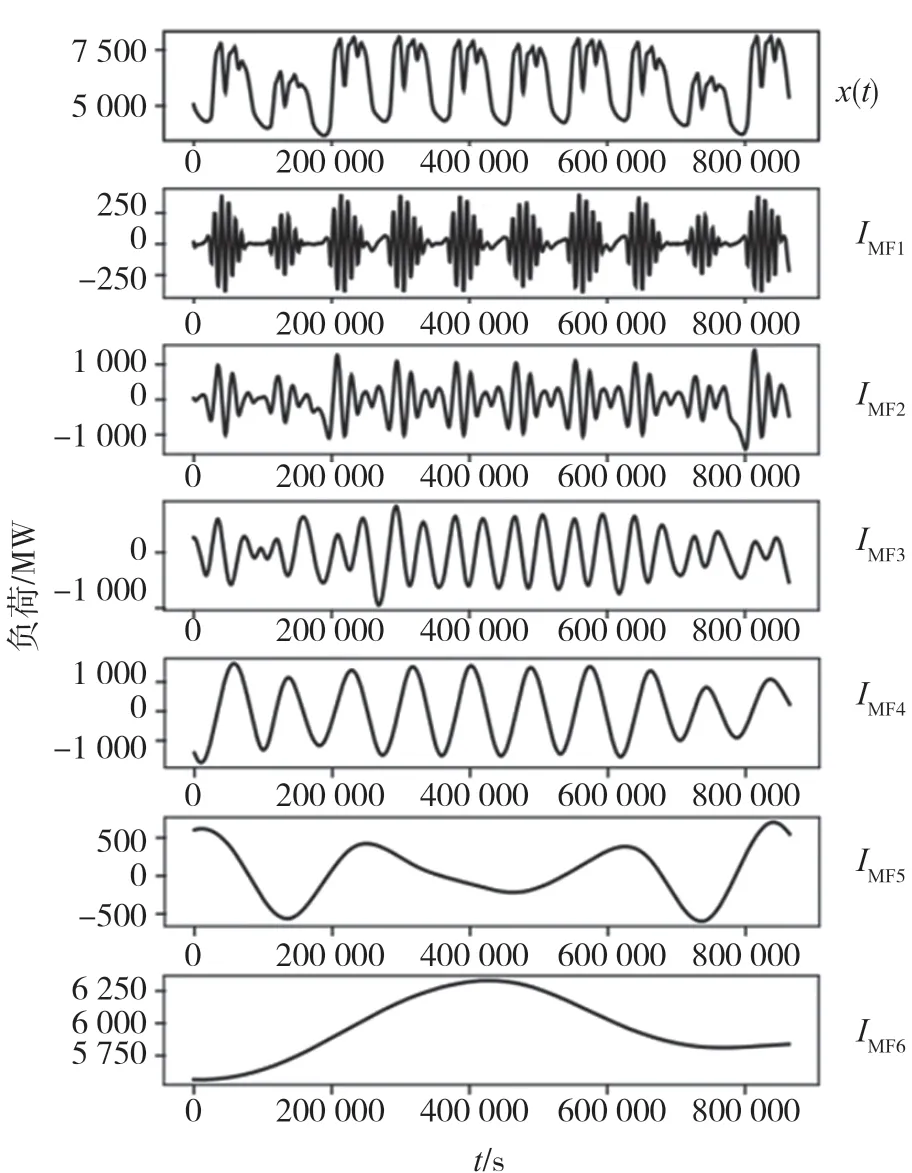
圖7 CEEMDAN 分解結果

3.3 模型參數設置

模型中基學習器采用LSTM、XGBoost、KNN，元學習器采用MLP。設置LSTM 堆疊層數為2 層，學習率為0.001，優化器為Adam。XGBoost 中的n_estimators 設置為36；KNN 中的n_neighbors 設置為30。元學習器MLP 中隱藏層為1 層，隱藏層中神經元數量為256 個。

3.4 模型預測效果分析

3.4.1 CEEMDAN 分解后的Stacking 模型與單一模型對比實驗

不同模型的預測精度對比結果如表1 所示。

表1 不同模型預測精度對比

由表1 可知，CEEMDAN-Stacking 模型相比CEEMDAN-LSTM 模型、CEEMDAN-XGBoost 模型以及CEEMDAN-KNN 模型，其RMSE、MAE 以及MAPE均達到了最低，說明Stacking 模型綜合了LSTM 模型、XGBoost 模型以及KNN 模型各自的優勢，從整體上提升了模型的預測精度[10,11]。

3.4.2 CEEMDAN-Stacking 與Stacking 對比實驗

分解后的模型預測精度對比如表2 所示。

表2 分解后模型預測精度對比

CEEMDAN-Stacking 模型相對于未經過分解處理的Stacking 模型，其RMSE、MAE、MAPE 均有所降低，證明了負荷序列經過CEEMDAN 分解處理后可以有效提升模型的預測精度。

負荷預測曲線如圖8 所示。

圖8 CEEMDAN-Stacking 與Stacking 模型預測結果對比

未經過分解處理的Stacking 模型雖然能夠預測負荷的變化趨勢，但是其對真實負荷序列的擬合能力較弱[12]。經過CEEMDAN 分解處理后，Stacking 模型對電力負荷的預測值與真實值更為接近，模型的預測能力得到了較大的提升。

3.4.3 改進型CEEMDAN-Stacking 與CEEMDANStacking 對比實驗

改進后的模型預測精度對比如表3 所示。

表3 改進后模型預測精度對比

由表3 可知，改進型CEEMDAN-Stacking 模型相對于CEEMDAN-Stacking 模型，其RMSE、MAE、MAPE 均有所降低。負荷預測曲線如圖9 所示。

圖9 改進型CEEMDAN-Stacking 與CEEMDAN-Stacking 模型預測結果對比

在大多數時間段內，改進型CEEMDAN-Stacking模型對真實負荷序列的擬合能力更強。改進型CEEMDAN-Stacking 模型根據學習器不同的預測效果賦予其相應的權重，優化了第2 層元學習器的輸入，從而得到更加準確的預測結果。

4 結 論

改進型CEEMDAN-Stacking 負荷預測模型以電力負荷時間序列為主線，對滑動窗口處理后的負荷序列進行CEEMDAN 分解并重構其模態分量。在預測模型部分，結合LSTM 算法、XGBoost 算法、KNN算法以及MLP 算法的優點，采用Stacking 集成學習模型將其融合，并通過精度賦權的方式對傳統Stacking 模型進行改進，進一步提升了模型的預測性能。相較于CEEMDAN-LSTM 模型、CEEMDANXGBoost 模型、CEEMDAN-KNN 模型、Stacking 模型以及CEEMDAN-Stacking 模型，改進型CEEMDANStacking 模型具有更高的預測精度和工程實用價值。