問題解決任務中行動序列的二分類建模：單/兩參數行動序列模型*

付顏斌 陳琦鵬 詹沛達

問題解決任務中行動序列的二分類建模：單/兩參數行動序列模型*

付顏斌 陳琦鵬 詹沛達

(浙江師范大學心理學院; 浙江省兒童青少年心理健康與心理危機干預智能實驗室; 浙江省智能教育技術與應用重點實驗室, 金華 321004)

行動序列作為一種典型的過程數據, 可反映被試解決問題的詳細步驟。鑒于行動或狀態轉移可區分正誤, 本文基于二分類Logistic建模提出兩個復雜度相對較低的行動序列模型——單/兩參數行動序列模型(1P-/2P-ASM); 兩者差異在于是否允許自由估計問題狀態的區分度。通過實證研究和模擬研究對比探究兩個新模型與基于多分類Logistic建模的序列作答模型(SRM)的表現。研究結果主要發現：(1)兩個ASM能夠獲得與SRM幾乎一致的問題解決能力估計值; (2)兩個ASM的計算耗時明顯低于SRM的; (3) 2P-ASM比1P-ASM的綜合表現更優。總之, 兩個模型復雜度相對低的ASM均能夠實現對行動序列的有效分析, 有益于行動序列數據分析的落地。

過程數據, 行動序列, 問題狀態轉換, 行動序列模型, 項目反應理論

1 引言

問題解決是指在沒有清晰解決方案的任務情境中, 個體通過一系列認知加工過程, 應用認知技能和認知活動, 在問題空間中進行探索, 將問題從初始狀態轉變為問題解決目標狀態的過程(Newell & Simon, 1972)。問題解決過程中, 被試需要根據問題解決的目標構建計劃, 選擇策略并預估該計劃的執行能否達到期望的狀態; 同時, 被試還需要根據問題目標對行動結果進行檢查, 發現問題并采取補救措施, 及時調整先前的行動策略。因此, 對問題解決能力的測量, 不僅要關注問題解決的最終結果, 還需要關注問題解決過程中系列行為(劉耀輝等, 2022)。比如, 國際學生測評項目(PISA) (OECD, 2013)推出了模擬生活情境的問題解決測驗, 通過真實且具有互動性的任務, 記錄學生在整個問題解決過程中行為的動態變化過程, 這為問題解決能力的測量提供了一種全新的方式。這些測驗不僅記錄了學生問題解決的結果, 還可以將學生在問題解決過程中的操作步驟實時記錄在日志文件中, 即過程數據(process data)。相較于傳統的結果數據, 基于過程數據的挖掘分析, 可以為推斷學生的潛在問題解決能力提供更為豐富的信息。

目前, 針對計算機化問題解決任務所產生的過程數據的分析方法研究, 根據研究目的主要可分為特征提取與能力評估建模兩類(Han et al., 2022; Xiao & Liu, 2023; 韓雨婷等, 2022)。其中, 特征提取可分為理論驅動和數據驅動兩類, 理論驅動的特征提取方法一般采用專家定義的行為指標來對學生的問題解決過程進行評分(Harding et al., 2017; Rosen, 2017; Yuan et al., 2019), 這種方法依賴于專家的知識經驗, 屬于自上而下的特征提取方法。理論驅動方法標定的行為指標不僅能夠用作對學生的評分依據, 還可以基于一定的測量模型進一步建模分析(Liu et al., 2018; Zhan & Qiao, 2022; Zhang et al., 2022), 但該方法往往要針對不同的任務情境設定不同的特征提取規則, 使得應用成本較高。數據驅動的方法指的是應用數據挖掘、機器學習等算法從過程數據中提取關鍵信息, 常使用的方法包括自然語言處理(Hao et al., 2015; He & von Davier, 2016; He et al., 2021; Zhan et al., 2015)、降維算法(Tang et al., 2020, Tang et al., 2021)和網絡分析方法(Vista et al., 2017; Zhu et al., 2016)等。

另外, 根據模型對行動序列順序關系的利用與否以及能否獲得連續穩定的能力估計值, 能力評估建模可進一步分為傳統心理計量模型的遷移應用、隨機過程建模以及這兩類的結合(韓雨婷等, 2022)。傳統心理計量模型的遷移應用主要是先利用特征提取方法提取完成任務的關鍵指標, 然后參照這些關鍵指標對被試呈現的具體操作或行動序列(action sequence)1文中, “行動序列”是指被試為完成任務而呈現出的一系列行動或狀態轉換(state transition), 其中“狀態轉換”在本文中與“行動”交替使用, 均指的是兩個相鄰問題狀態之間的轉換。例如, A→B或AB表示從當前階段的問題狀態A到下一階段的問題狀態B的狀態轉換, 進而“A→B→C"表示一個包括兩個行動或狀態轉換的行動序列（AB和BC）。同時, 本文中我們根據語言場景需求交替使用“行動序列”和“狀態轉移序列”兩個含義相同的名詞。進行編碼(如, 若具體操作中包含關鍵指標則被編碼為1, 否則為0), 最后基于題目作答理論(item response theory, IRT)模型或認知診斷模型對編碼數據進行分析, 并估計被試的問題解決能力(Han & Wilson, 2022; Liu et al., 2018; Wilson et al., 2017; Yuan et al., 2019; Zhan & Qiao, 2022; Zhang et al., 2022; 李美娟等, 2020)。然而, 這種方法會部分或完全忽視具體操作中的順序信息。與之相對, 已有研究直接對行動序列進行隨機過程建模, 如動態貝葉斯網絡(Levy, 2019)和隱馬爾可夫模型(Arieli-Attali et al., 2019; Bergner et al., 2017; Xiao et al., 2021)。這種方法雖然考慮到了行動序列中的順序信息, 但估計得到的潛變量通常是是離散的屬性或知識掌握狀態, 無法了解被試穩定且連續的問題解決能力(韓雨婷等, 2022)。另外, 還有研究提出了結合隨機過程思想的心理計量建模方法(Chen, 2020; Han et al., 2022; Lamar, 2018; Shu et al., 2017; Xiao & Liu, 2023)。通常, 這類方法假設在給定潛在問題解決能力的前提下, 被試的不同狀態轉換或操作轉移之間滿足條件獨立性假設; 比如, 將問題狀態轉換序列看作具有一階馬爾可夫特性的離散隨機過程(Han et al., 2022; Xiao & Liu, 2023), 從而在保留序列本身順序信息的同時推斷出連續的潛在能力估計值。

針對已有方法的局限性, Han等人(2022)將動態貝葉斯網絡與稱名作答模型(nominal response model, NRM) (Bock, 1972)相結合, 提出了序列作答模型(sequential response model, SRM)。SRM假設被試的問題解決能力和某狀態轉移的特征共同決定了被試呈現該狀態轉移的概率。相比于已有方法, SRM不僅考慮了行動序列的順序信息, 考慮了任務中不同狀態轉移的獨特性, 還可以提供問題解決能力的連續估計值, 可用于精細化了解不同被試問題解決能力之間的個體差異。與NRM類似, SRM假設被試在每個問題狀態下的所有轉移可選項(即行動可選項)都會提供測量信息, 進而為任務中每一個可能存在的狀態轉移都賦予不同的參數(如, 轉移傾向性參數和轉移區分度參數)。本質上講, SRM是對狀態轉移的多分類(或多元無序)建模, 即假設下一個階段中的所有轉移可選項之間沒有數量順序。然而, 在實際問題解決任務中, 行動或狀態轉移是有正誤之分的：可將有助于成功解決任務的狀態轉移界定為正確狀態轉移, 而將最終可能會導致任務失敗的狀態轉移界定為錯誤狀態轉移。因此, 被試在每個問題狀態下的所有轉移可選項是有正誤之分的, 并非完全是沒有數量順序的等價關系。

理論上, 對于有正誤之分的數據, 二分類建模更為適宜。與二分類建模相比, 多分類建模(Han et al., 2022; Xiao & Liu, 2023)的相對優勢是可以將更豐富的測量信息納入到數據分析中, 但這勢必導致模型的復雜性相對更高; 更高的模型復雜性通常意味著更多的待估計參數種類和數量, 更高的參數估計計算負擔, 更低的參數估計結果可解釋性(Ma et al., 2016)。基于模型比較與選擇的簡約原則(Beck, 1943), 本研究擬對包含正誤信息的行動序列進行二分類建模, 提出單參數和兩參數行動序列模型(one- and two-parameter action sequence model, 1P- / 2P-ASM), 以期降低行動序列分析模型的復雜性并增加計算效率; 同時, 相對簡約的模型也有助于增加模型參數估計結果的可解釋性, 進而增加行動序列模型的實踐易用性。

首先, 闡述行動序列建模基礎; 其次, 介紹本文兩個新模型：1P-ASM和2P-ASM; 然后, 基于一則實證研究數據對比兩個新模型和SRM的參數估計結果, 以展現新模型的實踐可應用性及其與SRM的參數估計結果一致性程度; 再然后, 通過模擬研究探究兩個新模型在不同模擬測驗條件的心理計量學性能; 最后, 對研究結果進行總結并探討研究局限及未來研究方向。

2 背景知識

2.1 行動序列建模基礎

本研究聚焦于任務目標明確且已知信息完備的結構良好(well-defined)任務; 這類任務常以有限狀態自動機(finite state automata)為原型構建。這類任務通常擁有有限的問題狀態, 有限的用戶輸入信號(即行動或操作), 并且通過用戶的操作可以產生對應的輸出信號, 即擁有明確的狀態轉移規則(Buchner & Funke, 1993)。圖1(a)呈現了一個FSA問題解決任務的例子, 該問題解決過程包含了S、A、B、C、D和E共六種問題狀態。其中S為問題解決初始狀態, E為問題解決的目標狀態, 其余均為問題解決的中間狀態。由于該題目允許被試在任意中間狀態反悔回到初始狀態, 所以理論上會出現多種行動序列, 比如, S→A→C→E、S→B→S→ A→C→E、S→B→D→E等。在眾多行動序列中, 把達到任務目標的最短行動序列界定為最優狀態轉移序列或最優行動序列; 如最優狀態轉移序列S→A→C→E包含S→A、A→C和C→E三個狀態轉移。圖中, 紅色實線箭頭表示正確狀態轉移, 即有助于正確解決問題的狀態轉移; 而黑色虛線箭頭為錯誤狀態轉移, 即最終可能導致遠離任務目標的狀態轉移。

實際上, 我們可以將被試在每個問題狀態下的行動轉移視為被試在作答一道“選擇題”。圖1(b)是與圖1(a)相對應的問題解決流程圖。當被試處于階段1中問題狀態S時, 他/她需要在階段2中的兩個問題狀態A和B之間做出選擇; 同理, 當被試處于階段2中問題狀態A時, 他/她需要在階段3中三個問題狀態C、D和S之間做出選擇(S表示返回到初始狀態)。此時, 我們就可將適用于題目層面作答精度數據分析的傳統IRT模型遷移應用于此。比如, Han等人(2022)就將NRM遷移應用于此, 進而基于多分類建模提出了SRM。

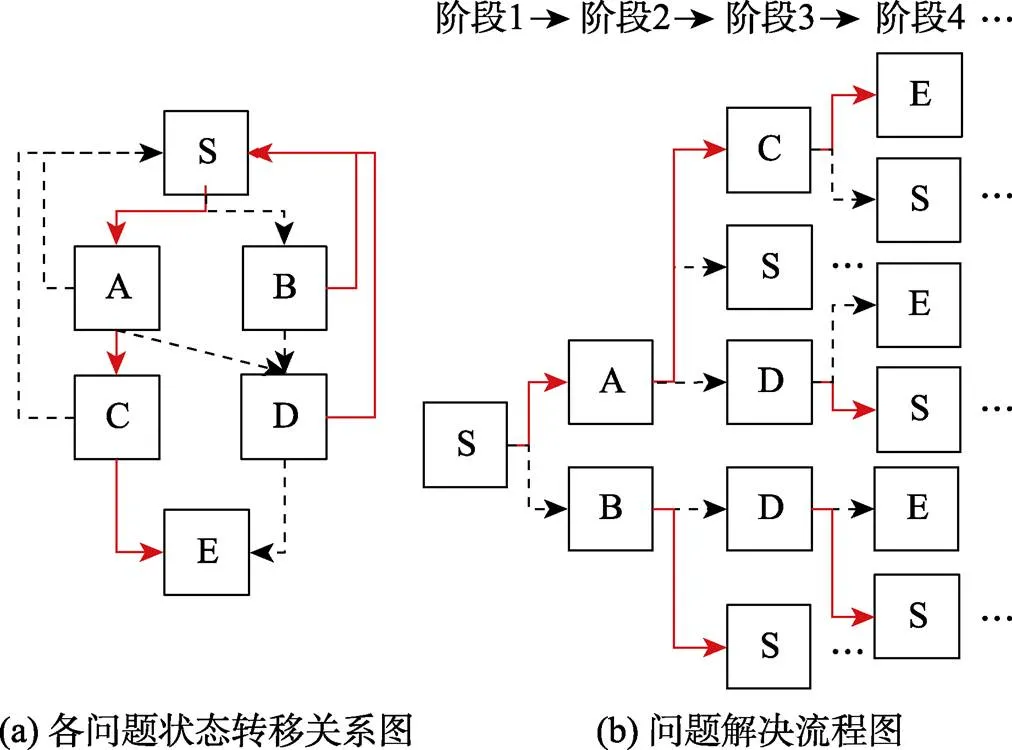
圖1 問題解決任務示意圖

注：紅色實線箭頭表示正確狀態轉移, 黑色虛線箭頭表示錯誤狀態轉移; S→A→C→E為最優行動序列, 其中包含S→A、A→C和C→E三個狀態轉移。省略號表示問題解決流程的重復出現。

2.2 SRM簡介

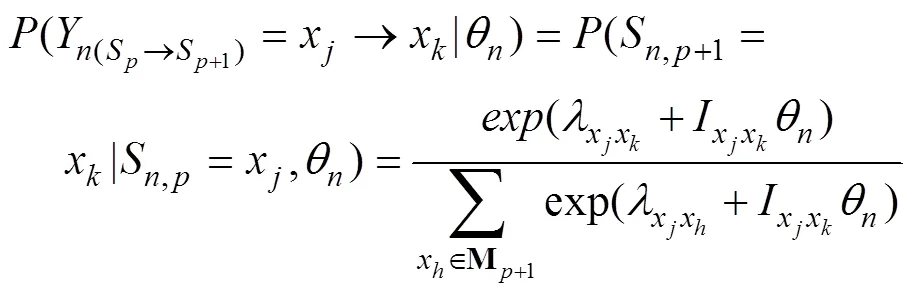
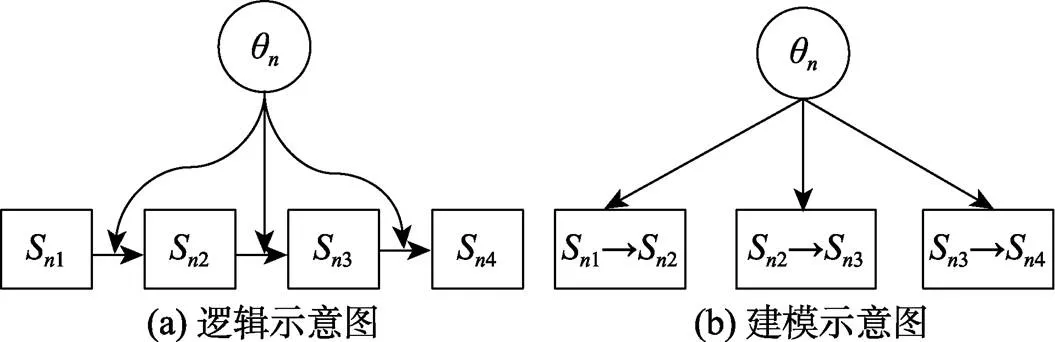
圖2 序列作答模型示意圖

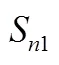
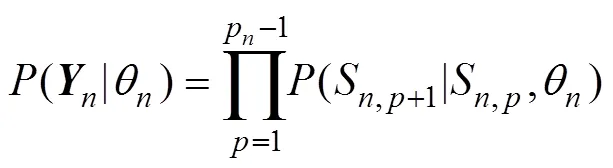
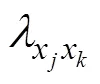
3 行動序列的二分類建模：1P-ASM和2P-ASM

3.1 模型構建

盡管SRM采用多分類建模將所有行動序列所提供的測量信息均納入到模型之中, 但它仍然通過一個預先設定的狀態轉移區分度參數區別對待了行動序列中狀態轉移的正確與否。針對具有正誤之分的狀態轉移, 本研究采用二分類建模思路, 使用針對二級評分數據的IRT模型對行動序列進行建模, 如單參數IRT模型/羅氏模型(Rasch, 1960)和兩參數IRT模型(Birnbaum, 1968)。對此, 圖3呈現了與圖1對應的問題解決任務的二分編碼示意圖, 該圖中我們將正確狀態轉移編碼為1, 錯誤狀態轉移編碼為0。圖3(b)中, 我們可以將每一階段中的“選擇題”視為“具有正確答案的多項選擇題”; 此時, 就可以借鑒傳統二級評分IRT模型來構建行動序列模型。

圖4呈現了兩個ASM的建模示意圖。首先, 將任務中所有的狀態轉移進行二分編碼：將正確狀態轉移編碼為1, 將錯誤狀態轉移編碼為0。此時, 被試解決問題所呈現的狀態轉移向量就被編碼為僅包含0或1元素的二元向量; 比如圖1中最優行動序列S→A→C→E所對應的狀態轉移向量(SA, AC, CE)’可被轉換為(1,1,1)′。然后, 基于二級評分IRT模型, 假設被試的問題解決能力影響被試呈現正確狀態轉移的概率。

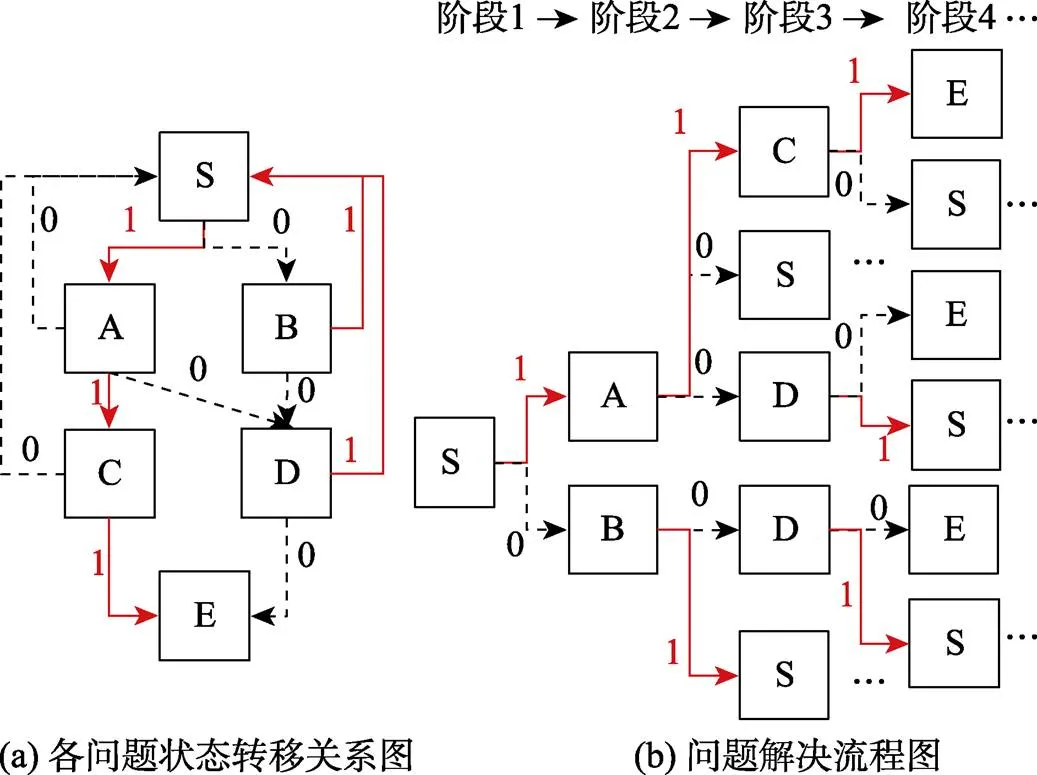
圖3 問題解決任務二分編碼示意圖

注：紅色實線箭頭表示正確狀態轉移, 編碼為1; 黑色虛線箭頭表示錯誤狀態轉移, 編碼為0; 省略號表示問題解決流程的重復出現。

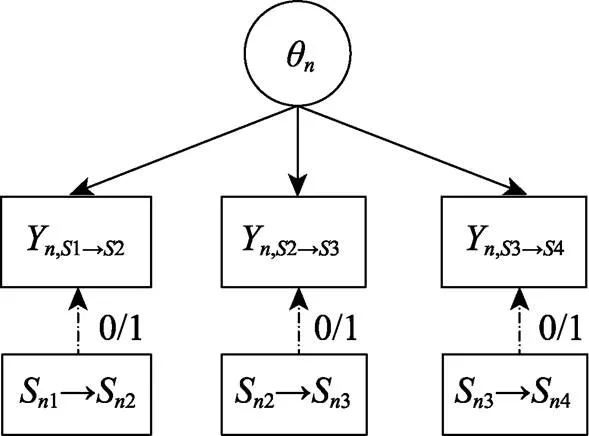
圖4 二分類行動序列模型建模示意圖

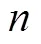
借鑒單參數IRT模型, 1P-ASM可被表示為：

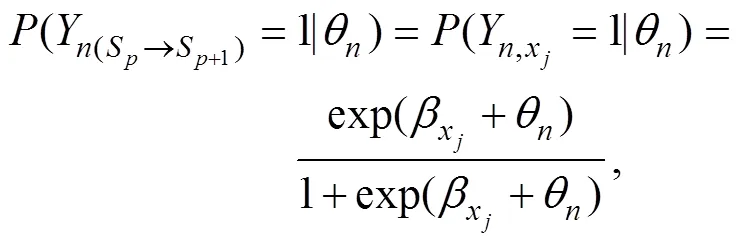
借鑒兩參數IRT模型, 2P-ASM可被表示為：

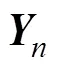
3.2 與相關模型的對比

3.3 貝葉斯參數估計

與SRM一樣, 兩個ASM也可使用全貝葉斯馬爾可夫鏈蒙特卡洛(MCMC)算法進行參數估計。詳見網絡版附錄7。

4 實證數據分析

4.1 任務描述

與Han等人(2022)研究保持一致, 本研究也選用PISA 2012計算機化問題解決“Tickets”任務(CP038Q02)的行動序列數據進行分析。該任務要求被試操作一臺虛擬售票機, 購買一張可以乘坐2次的全價郊區火車票。圖5呈現了該任務的初始界面, 問題解決過程中各階段的截圖見網絡版附錄2。為解決問題, 被試首先需要在交通方式上選擇“城市地鐵”或“郊區火車”。其次, 根據所選的交通方式, 被試需要在“全價票”和“打折票”之間做選擇。然后, 根據所選票價類型, 再選擇購買“包日票”或“次票”; 如果選擇“次票”則還要選擇購買的乘車次數(“1次”～“5次”)。最后做出“購買”決定即可完成該任務。被試可以在任意操作界面通過點擊“取消”來返回到任務的初始界面重新進行選擇。為了解決該任務, 不同被試最終呈現的行動序列的長度不盡相同。

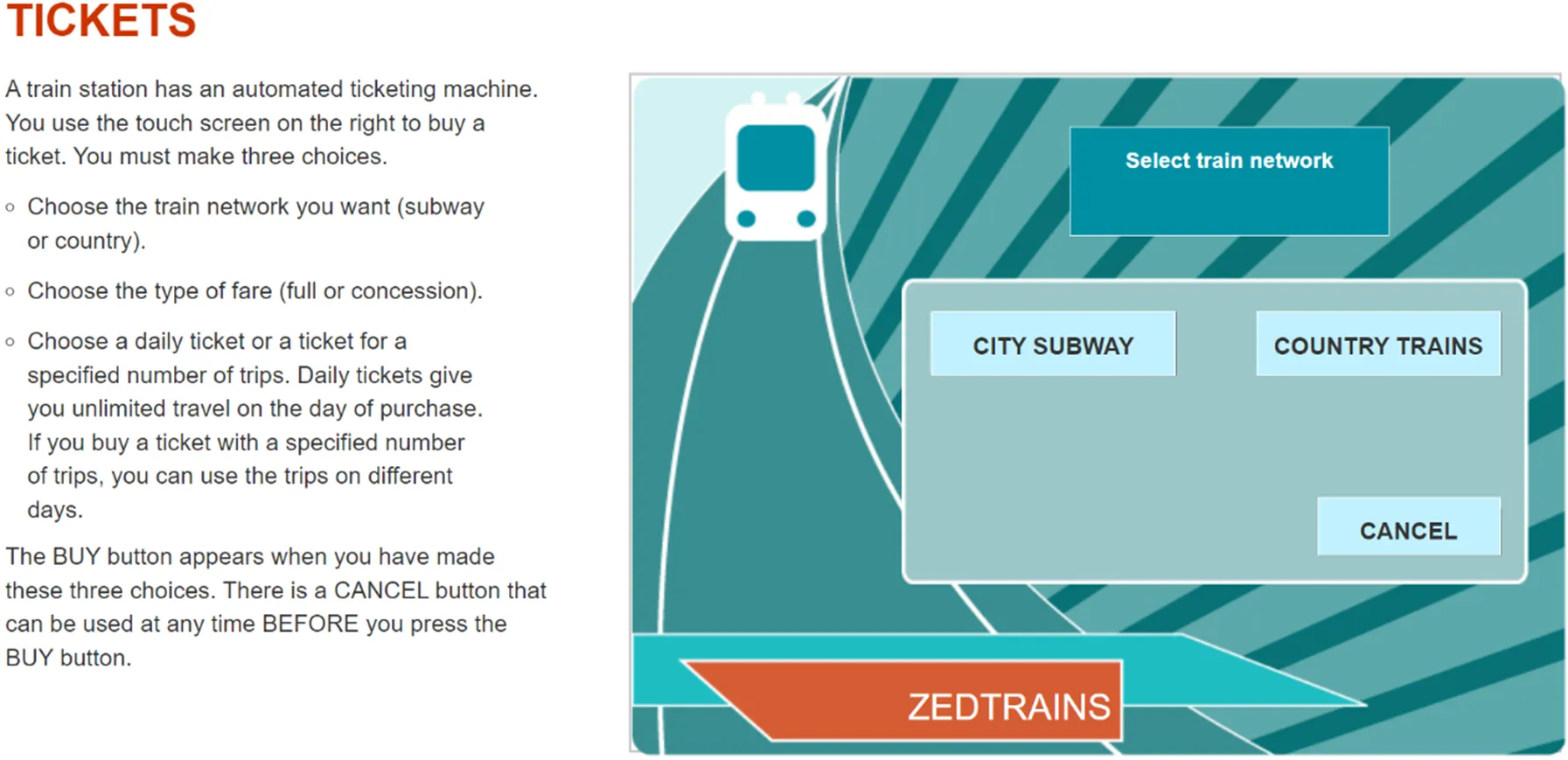
圖5 PISA 2012購票任務初始界面

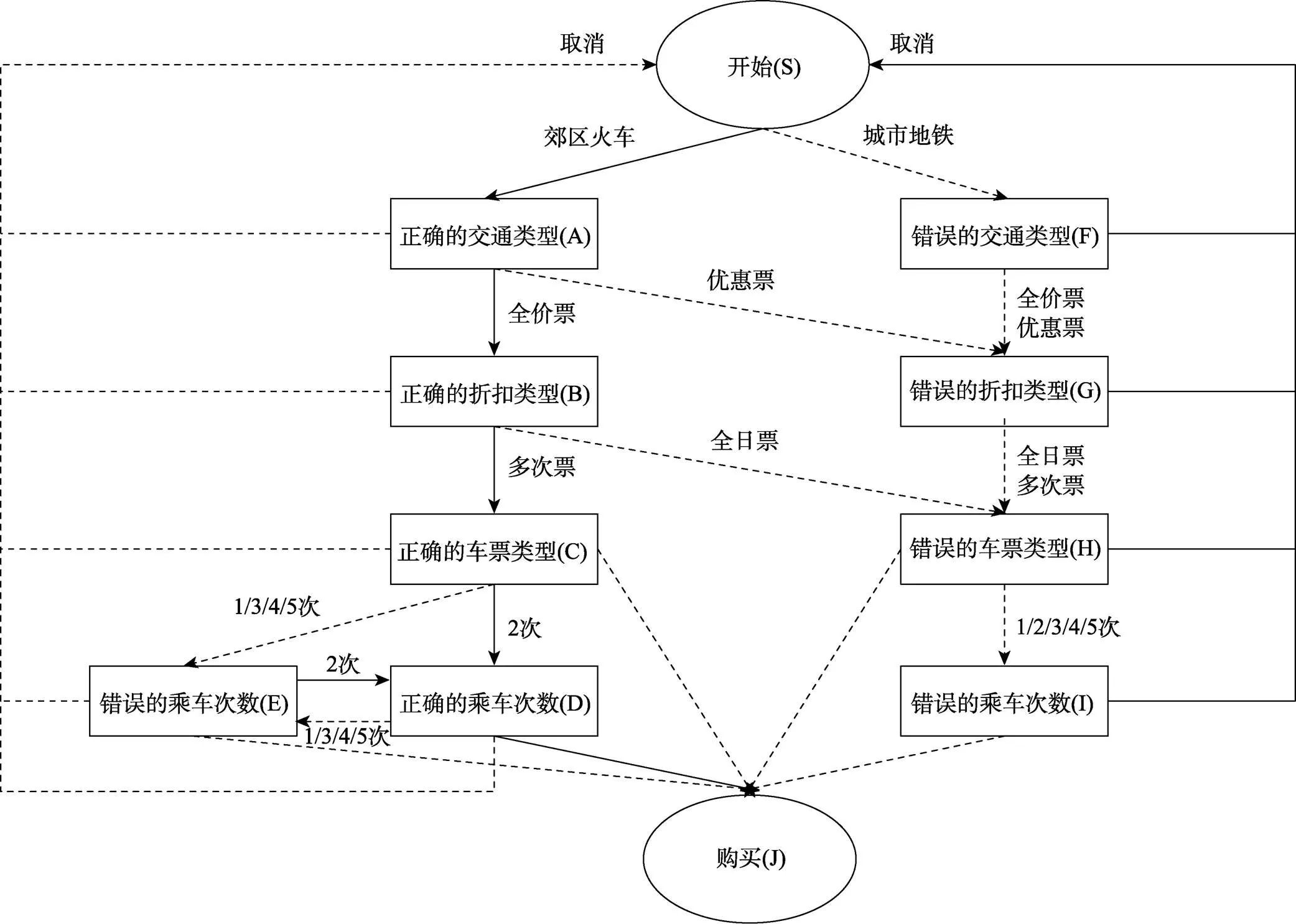
圖6 PISA 2012購票任務結構圖

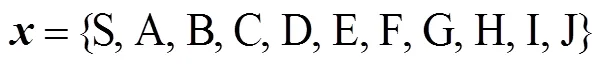
表1從“選擇題”視角進一步整理了圖6中的操作過程。可將當前階段所處的問題狀態視為一道被試需要作答的“選擇題”, 將下一階段的可選問題狀態視為“選項”。比如, 在初始階段被試需要在“選擇題”S的兩個“選項”A和F之間進行選擇; 其中A為正確“選項”, F為錯誤“選項”。針對這些“選擇題”, SRM將它們視為稱名作答題, ASM將它們視為二級評分選擇題。比如, 某學生的行動序列為SABCDEDJ, 則SRM分析的狀態轉移向量為(SA, AB, BC, CD, DE, ED, DJ)′, 而ASM分析的狀態轉移二分向量為(1, 1, 1, 1, 0, 1, 1)′。

表1 PISA 2012購票任務所類比的“選擇題”

注：括號中的1代表正確“選項”(即正確狀態轉移), 0代表錯誤“選項”(即錯誤狀態轉移)。

4.2 數據整理與分析

原始數據來源于PISA官網下載2https://www.oecd.org/pisa/pisaproducts/database-cbapisa2012.htm。在進行具體的數據分析之前, 先根據圖6中定義的任務結構對原始數據進行重新編碼, 并對數據進行清理：(1) 刪去提前終止作答的行動序列, 即沒有點擊“購買”的行動序列; (2) 刪除包含了不可能的狀態轉移的行動序列(如網絡版附錄3表A2)。最終, 從記錄行動的日志文件中提取了28,851名被試的行動序列, 其中行動序列的最短長度為5, 最長長度為110, 平均長度為6.992。原始數據當中包含了1,395種行動序列, 其中有569種行動序列完成了任務目標(涉及15,408名被試：有10,610名被試按照最優行動序列完成了任務目標, 另外4,798名學生在正確解決問題過程中有錯誤修正過程)。最后, 限于算力且為增加研究效率, 我們采用簡單隨機抽樣, 從28,851名被試中隨機選取了2,000名學生的行動序列用于本研究的實證分析(行動序列的最短長度為5, 最長長度為46, 平均長度為7.03; 包含了1395種行動序列, 其中有569種行動序列完成任務目標(涉及1068名學生, 有737人按照最優行動序列完成了任務目標)。

分別使用1P-ASM、2P-ASM和SRM分析數據。參數估計時, 選用2條馬爾可夫鏈, 每條鏈長5,000次, 預熱(burn-in)3,000次。使用PSRF值(PSRF; Gelman & Rubin, 1992)來確定MCMC算法得到的參數估計值是否達到收斂; 當PSRF < 1.1時, 表明參數估計收斂。此外, 采用Watanabe-Akaike信息準則 (WAIC; Watanabe, 2010)和留一法交叉驗證(LOO, Vehtari et al., 2017)兩個完全貝葉斯的相對擬合指標來衡量模型對數據的擬合情況, 為模型選擇提供證據; 兩個指標值越小, 表明模型對數據的擬合越好。值得注意的是, 由于SRM和ASM分析的數據并不相同(前者分析的是每位學生的狀態轉移向量, 后者分析的是每位學生的狀態轉移向量的二分化向量), 所以兩者的相對擬合值無法比較。因此, 我們僅能通過相對擬合指標判斷兩個ASM之間的相對擬合優劣, 無法用于判斷ASM和SRM的相對擬合優劣。對此, 本研究將通過計算ASM和SRM參數估計結果的一致性來體現二分類建模具有與多分類建模相接近的表現。另外, 使用后驗預測檢驗(PPC; Gelman et al., 1996)評估模型對數據的絕對擬合; 如果模型擬合數據, 則其后驗預測概率()接近0.5, 反之, 如果模型不擬合數據, 則其值 < 0.025或 > 0.975。本文中PPC所使用的統計量見網絡版附錄4表A3。

4.3 結果

所有模型中所有參數的PSRF值均小于1.05, 表明在我們的設定下所有參數估計達到收斂標準。此外, 網絡版附錄5中提供了模型參數的抽樣軌跡圖。表2呈現了三個模型對數據的擬合情況和計算耗時。首先, 三個模型的值均接近0.5, 表明三個模型均擬合該數據。其次, 兩個相對擬合指標表明2P-ASM對數據的擬合優于1P-ASM, 意味著考慮狀態轉移的區分度能更好地反映該數據的特征, 即不同狀態轉移對問題解決能力的區分能力是不同的。如上文所述, ASM和SRM的相對擬合結果不具有可比性。最后, 參數估計耗時可以綜合反映模型的復雜性程度, 結果發現SRM的耗時最長, 2P-ASM次之, 1P-ASM的耗時最短; 這表明二分類模型的確比多分類模型簡約。下文主要研究結果圍繞兩個ASM闡述, 并呈現ASM和SRM對被試問題解決能力估計的一致性。

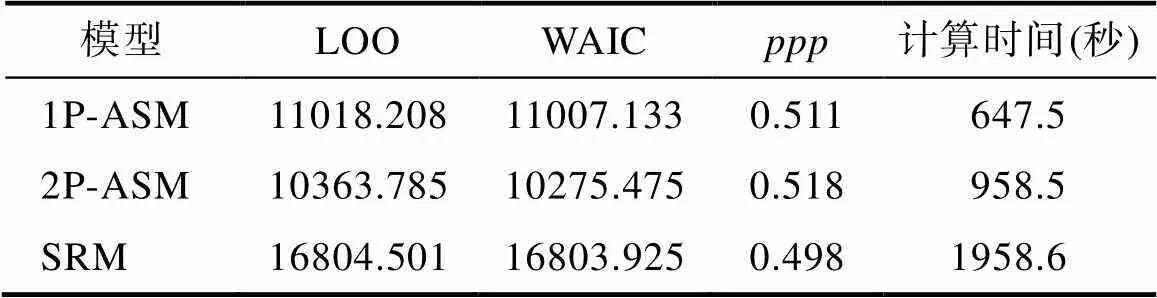
表2 實證研究中三個模型對數據的擬合情況和計算耗時

注: 1P-ASM = 單參數行動序列模型; 2P-ASM = 兩參數行動序列模型; SRM = 序列作答模型; LOO = 留一法交叉驗證; WAIC = Watanabe-Akaike信息準則;= 后驗預測概率。

表3中呈現了兩個ASM的題目參數估計結果3SRM的題目參數估計結果見于網絡版附錄8。(后驗均值、后驗標準差和95%最高概率密度[貝葉斯可信區間])。首先, 對于行動容易度參數而言, 正確問題解決路徑(即最優行動序列)上的問題狀態(S、A、B、C和D)的容易度參數的后驗均值均大于0 (2P-ASM中問題狀態D的后驗均值與零無顯著差異), 表明當被試處于正確路徑上的問題狀態時, 其更容易繼續呈現正確狀態轉移; 與之相對, 錯誤問題解決路徑(即非最優行動序列)上的問題狀態(F、G、H和I)的容易度參數的后驗均值均小于0 (1P-ASM中問題狀態I的后驗均值與零無顯著差異; 2P-ASM中問題狀態H和I的后驗均值與零無顯著差異), 表明當被試已經處于錯誤路徑上的問題狀態時, 其更難以糾正錯誤轉向正確的問題狀態(即更易于繼續維持在錯誤路徑上)。值得注意的是, 問題狀態E和I是錯誤路徑上的問題狀態, 其含義均為“選擇錯誤的乘車次數”; 相較于其他錯誤路徑上的問題狀態, E和I的容易度估計值更高, 表明當被試處于這兩個錯誤狀態時, 更有可能在下一步選擇時糾正自己的錯誤(即選擇S返回初始狀態重新作答)。其次, 對于行動區分度參數而言, 不同問題狀態的行動區分度有一定差異性。其中, 問題狀態C和I的行動區分度后驗均值相對較高, 表明不同問題解決能力的學生在這兩個問題狀態下呈現正確狀態轉移的概率差異相對較大。也就是說, 已處于正確問題解決路徑上的學生是否能夠選擇正確的乘車次數, 以及已經處于錯誤問題解決路徑上的學生是否能夠通過“取消”來糾正自己的錯誤, 這兩個操作對于學生的能力的區分力是相對最強的。總之, 根據行動參數估計值可發現, 當被試已經處于正確問題解決路徑, 則其更易于保持在正確問題解決路徑上; 而當被試已經處于錯誤問題解決路徑, 則其更易于繼續錯下去, 直到末尾選擇乘車次數界面時才有一個糾正錯誤的關鍵期。

圖7呈現了三個模型的問題解決能力估計值(后驗均值)的對比散點圖及概率密度圖。首先, 散點圖結果呈現出三個模型的問題解決能力估計值具有較高的一致性(三者之間的相關系數均在0.99以上), 表明它們測量的是同一潛在特質且二分類建模與多分類建模一樣能夠通過分析行動序列數據測量被試的問題解決能力并反映個體之間的差異性。其次, 對比三模型的概率密度圖, 可發現三個模型在高能力區間和低能力區間的概率密度分布基本一致, 僅在中能力區間的分布略有差異(主要是SRM)。一個可能的原因是SRM更充分地利用了不同狀態轉移所提供的測量信息：它不僅利用了正確狀態轉移所包含的測量信息, 也利用了不同錯誤狀態轉移中的測量信息。比如, 當多名被試同時處于問題狀態A時, 相比于選擇錯誤“選項”G的被試而言, 選擇錯誤“選項”S的被試的問題解決能力似乎要更高一些; 此時, SRM是可以區分呈現AG的被試和呈現AS的被試之間的區別的, 而ASM則將他們均視為同一類做出錯誤選擇的人。

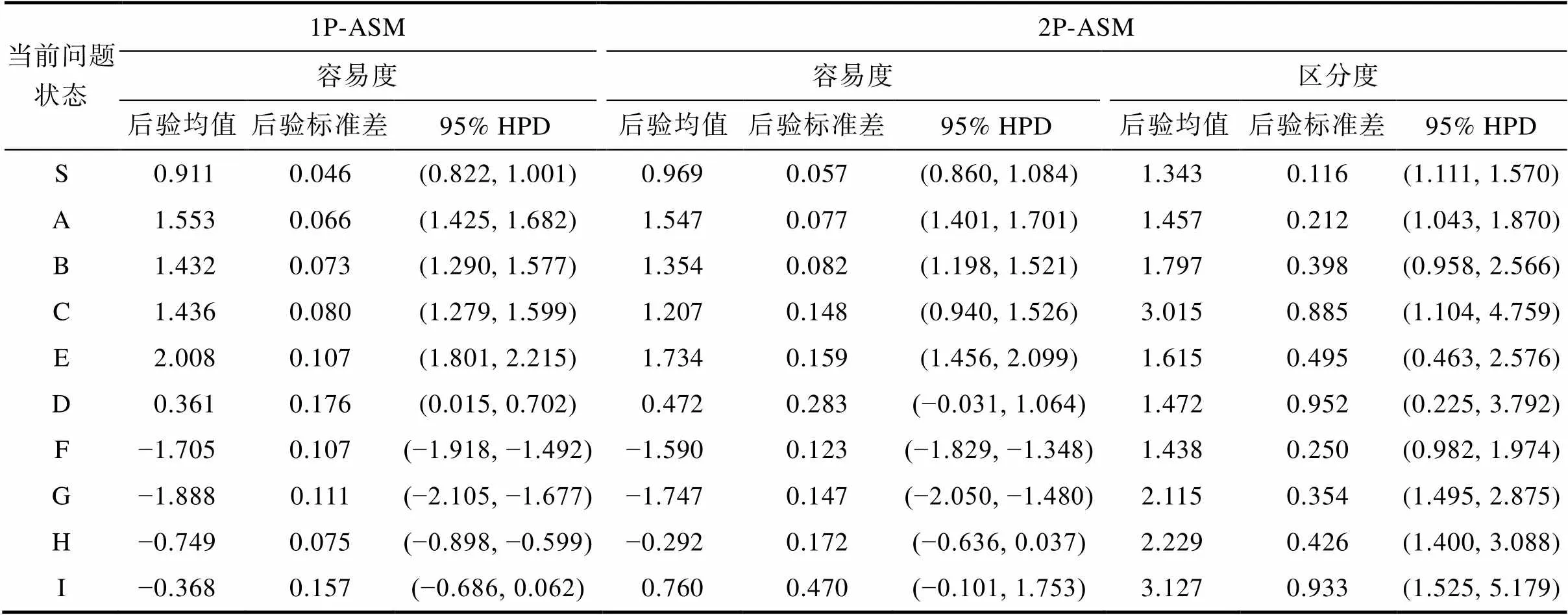
表3 實證研究中行動序列模型參數估計結果

注: 1P-ASM = 單參數行動序列模型; 2P-ASM = 兩參數行動序列模型; SRM = 序列作答模型; 95% HPD = 95%最高概率密度(貝葉斯可信區間)。

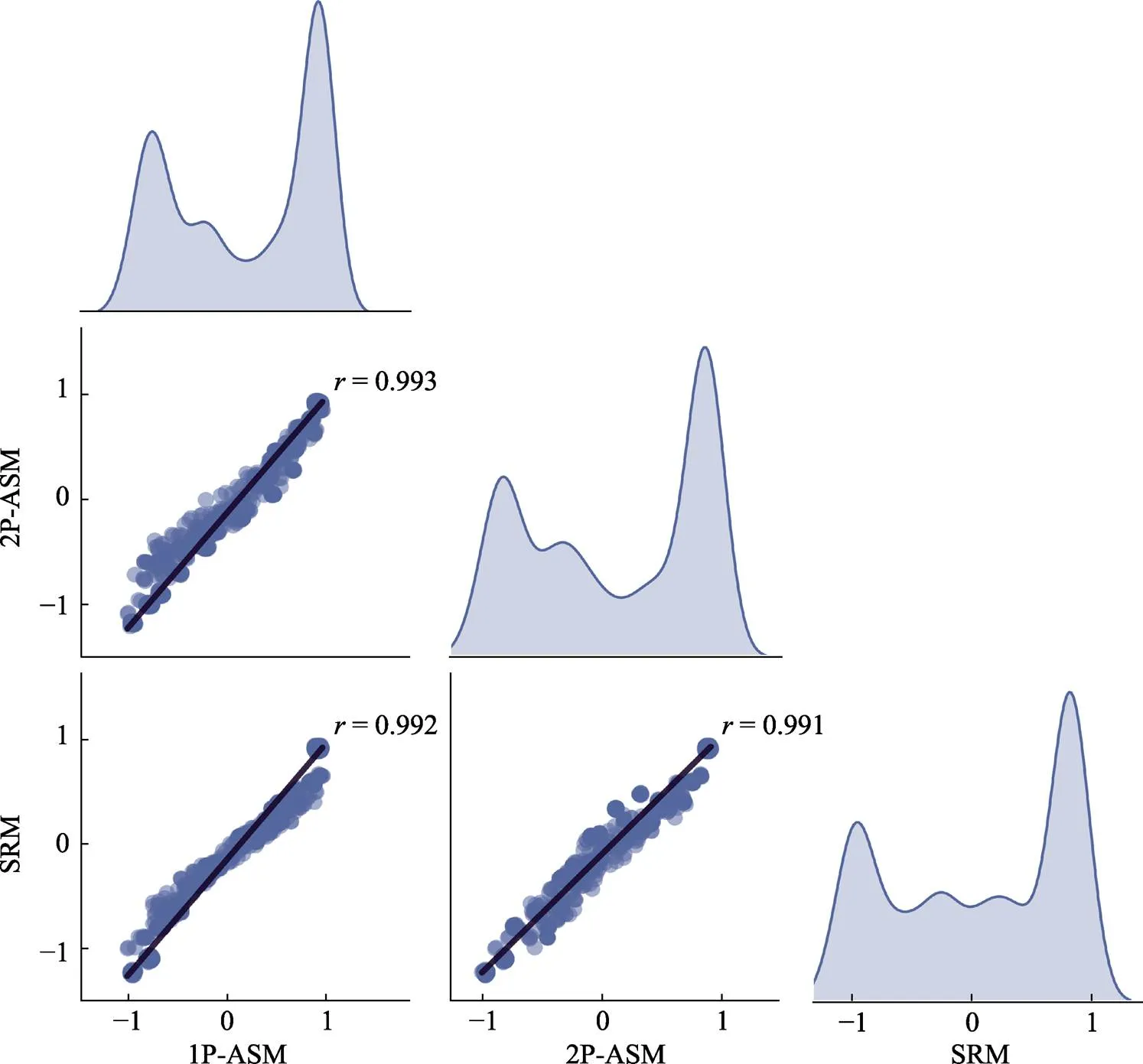
圖7 實證數據中三個模型的問題解決能力參數后驗均值對比散點圖及概率密度圖

注: 1P-ASM = 單參數行動序列模型; 2P-ASM = 兩參數行動序列模型; SRM = 序列作答模型; r = 皮爾遜積差相關。

從分析數據中挑選取出現頻率大于20次的行動序列作為典型行動序列(涵蓋了80.1%的被試)。表4呈現了典型行動序列在三個模型中的問題解決能力估計值的描述統計(按SRM的能力估計均值從高到低排序)。首先, 三個模型對呈現各典型行動序列的被試的能力估計的描述性統計具有一定的一致性。比如, 呈現最優行動序列SABCDJ的被試的能力估計均值相對最高, 而呈現最差行動序列SFGHIJ的被試的能力估計均值相對最低。其次, 整體而言, 各典型行動序列中, 出現正確問題狀態的數量越多且出現錯誤問題狀態的數量越少則被試的能力估計值的均值就越高, 反之, 被試的能力估計值的均值就越低。然后, 對比ASM和SRM的結果, 發現ASM中有兩個序列下的被試的能力估計值的均值排序與SRM中的不同：SABCEDJ對應的能力估計值的均值略低于SFGHSABCDJ對應的。呈現SABCEDJ的被試盡管在狀態C上的選擇出現了錯誤轉移(CE)且馬上進行了糾正(ED), 而呈現SFGHSABCDJ的被試在初始狀態就出現了錯誤轉移, 直到選擇購買乘車次數時才返回初始頁面糾正自己的錯誤。ASM和SRM在這兩個序列上的排序差異可以從不同的視角解釋。首先, 從出現錯誤狀態的次數或問題解決效率(序列長度)看, 似乎呈現SABCEDJ的被試的能力估計值均值應該高于呈現SFGHSABCDJ的被試的; SRM的排序結果支持該視角解釋。其次, 結合表3中的行動容易度參數可發現, 問題狀態C的容易度較高(難度較低), 而問題狀態F、G和H的容易度較低(難度較高); 因此, 從錯誤選擇對能力估計帶來的負面影響或懲罰看, 在狀態C的錯誤選擇所帶來的懲罰高于在狀態F、G和H的錯誤選擇所帶來的, 進而導致SABCEDJ的被試的能力估計值均值低于呈現SFGHSABCDJ的被試的; ASM的排序結果支持該視角解釋。

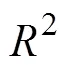
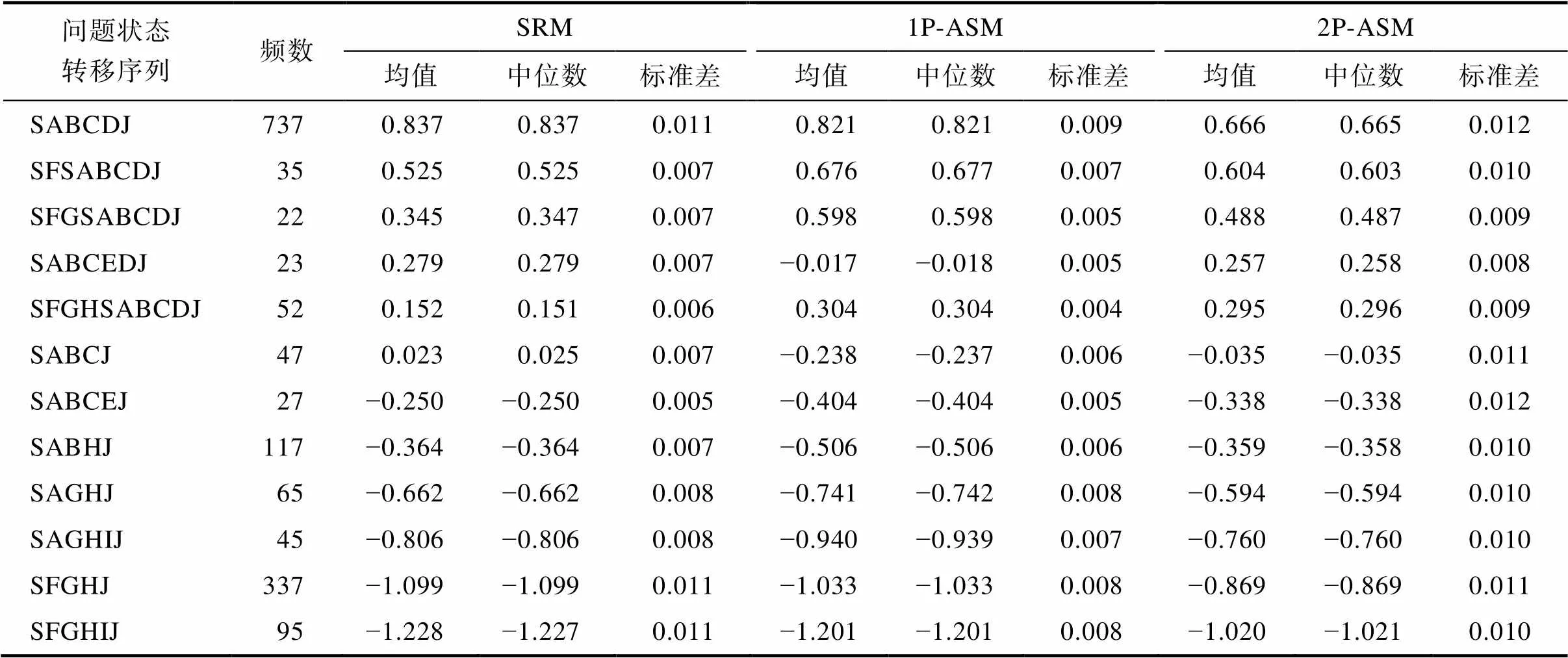
表4 典型行動序列對應的問題解決能力估計值的描述統計

注：1P-ASM = 單參數行動序列模型; 2P-ASM = 兩參數行動序列模型; SRM = 序列作答模型。

5 模擬研究

5.1 研究設計、數據生成與分析

通過一則模擬研究進一步探究兩個ASM在理想測驗情境下的心理計量學表現。需要強調的是ASM本身并無法生成被試解決任務所呈現的行動序列(只能生成0-1向量); 因此, 模擬研究中使用SRM作為行動序列數據的生成模型。采用實證研究中的問題解決任務結構(圖6)來生成行動序列數據。模擬研究包含兩個操縱變量：樣本量(含100、200和500人三個水平)和行動序列長度(含短和長兩個水平); 參照Han等人(2022)和Fu等人(2022)的做法, 在SRM中通過調整“取消”操作(如, A→S)的轉移傾向參數來操縱行動序列的長度：該參數取值越大行動序列長度越長。行動序列生成步驟詳見網絡版附錄6。最終, 本研究中生成的短行動序列和長行動序列的平均長度分別約為10.5和20.2。此外, 為減少隨機誤差影響, 六種模擬條件下均按照上述數據生成步驟重復生成50組數據。

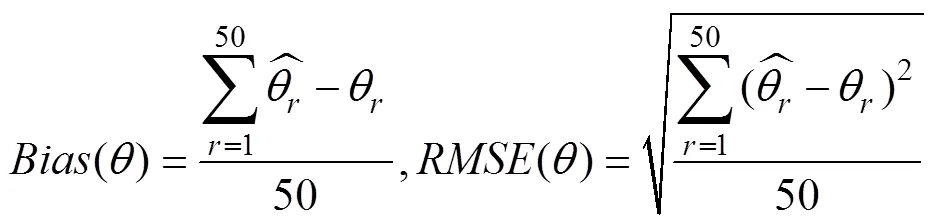
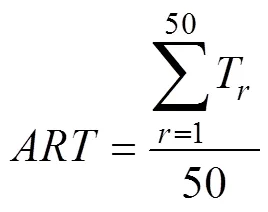
5.2 結果

首先, 在所有條件下, 三模型中所有參數的PSRF均小于1.1, 表示所有模型參數估計均收斂。表5呈現了不同模擬條件下三個模型的問題解決能力參數估計的返真性和計算耗時。首先, 被試樣本量對能力參數估計的返真性的影響較小; 序列平均長度越長, 能力參數估計的返真性越高。從另外的角度來看, 序列的平均長度反映了題目樣本量的大小, 序列平均長度越長, 即題目的樣本量越大, 對于被試能力值的推斷則越準確。其次, SRM作為數據生成模型, 其返真性理應最好, 2P-ASM次之, 1P-ASM最差, 但三者間整體差異不大(絕大多數條件下1P-ASM的RMSE比SRM的高不到0.05, Cor低不到0.02)。最后, 在所有條件下1P-ASM的計算耗時最短, 2P-ASM次之, SRM最長; 該結果與實證研究結果吻合, 表明相比于多分類模型, 二分類建模在保證其能力參數估計精度僅有微弱下降的同時, 可大幅減少參數估計耗時。

表6呈現了不同模擬條件下兩個ASM與SRM的問題解決能力參數估計的一致性。整體看, 兩個ASM與SRM的一致性均較高, 且2P-ASM與SRM的一致性高于1P-ASM與SRM的一致性。另外, 值得注意的是, 當序列長度增加后, 1P-ASM與SRM的一致性略有下降, 而2P-ASM與SRM的一致性略有提升。可能的原因是, 1P-ASM相對簡單, 其約束所有問題狀態具有相同的區分度, 而序列較短(“題目”數量較少)時這種約束帶來的負面影響比序列較長時低(序列越長, 各問題狀態之間的區分度差異越大); 而2P-ASM相對復雜, 需自由估計所有問題狀態的區分度, 此時, 隨著序列長度的增加, 各問題狀態的區分度差異隨之增加, 更符合2P-ASM的假設。

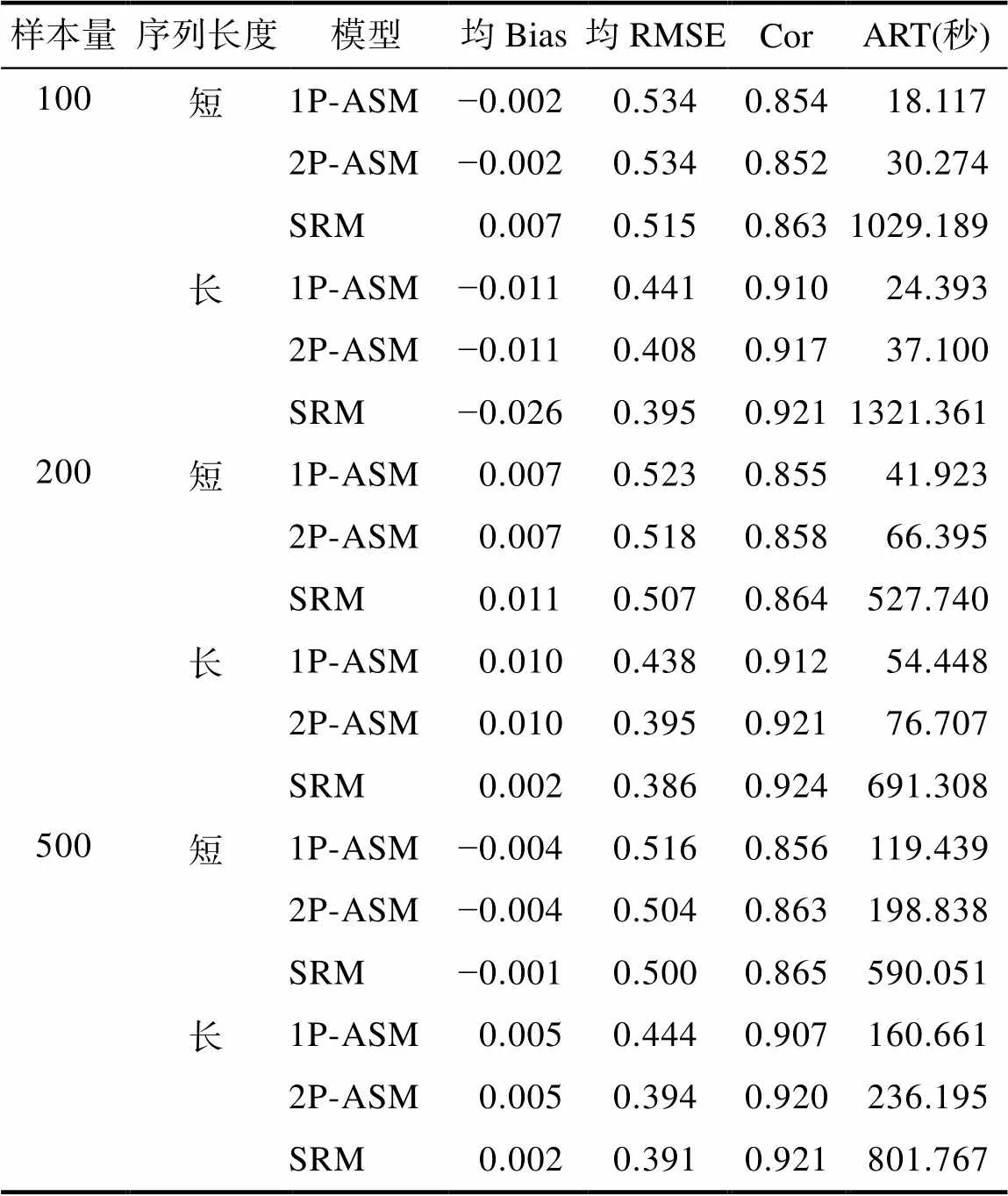
表5 模擬研究中三個模型的問題解決能力參數的估計返真性和計算耗時

注: 1P-ASM = 單參數行動序列模型; 2P-ASM = 兩參數行動序列模型; SRM = 序列作答模型; 均Bias = 所有被試的估計偏差的均值; 均RMSE = 所有被試的均方根誤差的均值; Cor = 真值與估計值之間的相關系數; ART = 平均計算時間。當樣本量為100時, SRM模型的計算耗時明顯多于其他較高樣本量條件下的計算耗時; 可能是因為樣本量較少的情況下, 數據提供的測量信息有限, 使復雜程度較高的SRM的MCMC抽樣更為困難。

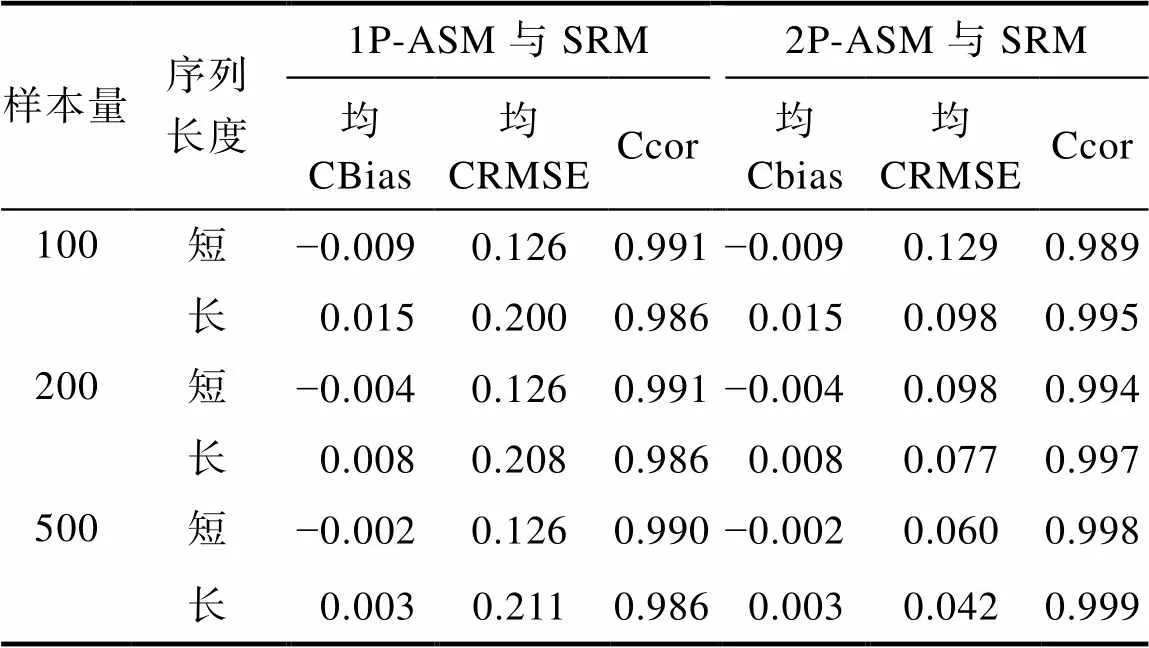
表6 模擬研究中兩個ASM和SRM的問題解決能力參數估計的一致性

注: 1P-ASM = 單參數行動序列模型; 2P-ASM = 兩參數行動序列模型; SRM = 序列作答模型; 均Cbias = 所有被試的一致性偏差的均值; 均CRMSE = 所有被試的一致性誤差的均值; Ccor = SRM估計值與ASM估計值之間的相關系數。

6 總結與討論

與傳統作答精度數據相比, 諸如行動序列等過程數據能提供有關被試如何解決問題的更豐富信息。同時, 行動序列數據的非標準化格式(即不同被試的數據長度不同)也給傳統心理計量學模型的直接應用帶來了困難。針對已有方法的局限, Han等人(2022)將動態貝葉斯網絡與NRM相結合, 提出了SRM。與NRM類似, SRM采用多分類logistic建模, 進而為任務中每一個可能存在的狀態轉移都賦予不同的參數, 導致模型復雜性較高。鑒于問題解決任務中狀態轉移有正誤之分, 而非是沒有數量順序的等價關系, 本文基于二分類建模提出了兩個模型復雜性相對較低的行動序列模型——1P-ASM和2P-ASM。不同于SRM將NRM遷移應用至行動序列數據分析, 1P-ASM和2P-ASM分別將更為簡單的單參數IRT模型和兩參數IRT模型遷移應用至行動序列數據分析。實證研究結果發現(1)兩個ASM和SRM的問題解決能力估計值具有接近于1的相關系數, 表明它們測量的是同一潛在特質; (2)兩個ASM的計算耗時明顯低于SRM的, 一定程度上表明ASM的模型復雜性低于SRM的; (3)參數估計結果揭示了本研究中任務的特征：當被試已經處于正確問題解決路徑, 則其更易于保持在正確問題解決路徑上; 反之, 當被試已經處于錯誤問題解決路徑, 則其更易于繼續錯下去; (4)與1P-ASM和SRM將區分度參數進行固定不同, 2P-ASM可以提供在當前所處問題狀態下呈現正確狀態轉移的區分度參數, 有助于確定相對比較重要的問題狀態(比如實證研究中的問題狀態C和I), 以便數據分析者更好地了解任務本身。模擬研究結果發現(1)即便不是數據生成模型, 兩個ASM也能提供較高的參數估計返真性; (2)兩個ASM的計算耗時低于SRM, 尤其是在小樣本量條件下的相對優勢更為明顯; (3)兩個ASM的問題解決能力估計值與SRM的均具有很高的一致性, 且2P-ASM與SRM的一致性相對更高; (4)被試解決問題時最終呈現的行動序列的長短是影響兩個ASM以及SRM參數估計返真性的主要原因之一：序列越長, 數據所含信息越多, 對問題解決能力的估計精度更高。綜上所述, 本文基于二分類建模提出的兩個ASM能夠實現對行動序列數據的有效分析, 在減少模型復雜性的同時, 還能夠提供與SRM幾乎一致的被試問題解決能力估計值。同時, 綜合模擬研究與實證研究的結果, 我們認為2P-ASM比1P-ASM的綜合表現更優; 但當樣本量較小(如100人)或任務簡單(解決問題所需的操作較少)時, 則推薦使用更簡約的1P-ASM。

當然, 作為二分類模型, ASM與SRM相比仍有一定的理論局限。比如, 使用ASM分析行動序列數據前需要將行動序列進行二分編碼, 將所有錯誤狀態轉移視為“等價”, 進而不可避免地損失了不同錯誤狀態轉移所提供的差異化信息。另外, 由于ASM是對二分編碼后的行動序列數據進行建模的, 導致我們無法通過給定模型參數使其生成行動序列數據。

盡管本文提出兩個可有效分析行動序列數據的模型, 但仍有一些不足值得在今后的研究中做進一步嘗試。比如, 首先, 與SRM一樣, ASM也假設被試的問題解決能力是單維的; 然而, 在一些問題解決任務中, 有可能需要被試使用多個不同維度的問題解決能力。后續研究也可嘗試進一步提出多維行動序列模型(Shu et al., 2017)。其次, 在過程數據中, 不僅記錄了被試在問題解決各階段所處的問題狀態, 還記錄了被試在問題解決各階段上的時間戳信息; 利用時間戳信息可以計算出被試呈現各狀態轉移所花費的時間, 即行動時間(action times) (Fu et al., 2022)。目前, 在題目層面數據分析中, 已有大量關于題目作答時間(item response times)數據分析的以及將其與題目作答精度數據進行聯合分析的研究(e.g., van der Linden, 2006; 2007; Man et al., 2022; Peng et al., 2022; Zhan et al., 2018, Zhan et al., 2022)。后續研究也可嘗試將行動時間數據與行動序列數據相結合, 進一步挖掘過程數據中所包含的豐富信息(Fu et al., 2022)。再有, 被試在解決問題過程中必須從下一個階段的轉移可選項中選擇一個才能將任務繼續下去; 當被試不知如何選擇時, 是有可能通過猜測來進行選擇的。后續研究也可以嘗試遷移應用包含猜測參數的三參數IRT模型來處理行動序列數據中可能存在的猜測問題。最后, 由于篇幅、時間和精力所限, 模擬研究中所操縱的變量數量或水平數量有限, 未能充分挖掘ASM在不同理想測驗條件下的表現。后續研究也可嘗試通過操縱其他變量(如, 任務的復雜性[包含更多數量問題狀態])來進一步探究ASM的心理計量學性能。

Arieli-Attali, M., Ou, L., & Simmering, V. R. (2019). Understanding test takers' choices in a self-adapted test: A hidden Markov modeling of process data.,, 83.

Beck, L. W. (1943). The principle of parsimony in empirical science.,(23), 617?633. https://doi.org/10.2307/2019692

Bergner, Y., Walker, E., & Ogan, A. (2017). Dynamic Bayesian network models for peer tutoring interactions. In A. A. von Davier, M.Zhu, & P. C. Kyllonen (Eds),(pp. 249?268). Cham: Springer.

Birnbaum, A. (1968). Some latent trait models and their use in inferring an examinee's ability. In F. M. Lord & M. R. Novick (Eds.),(pp.397?124). Reading, MA: Addison-Wesley.

Bock, R. D. (1972). Estimating item parameters and latent ability when responses are scored in two or more nominal categories.(1), 29?51. https://doi.org/10. 1007/BF02291411

Buchner, A., & Funke, J. (1993). Finite-state automata: Dynamic task environments in problem-solving research.(1), 83?118.

Chen, Y. (2020). A continuous-time dynamic choice measurement model for problem-solving process data.(4), 1052?1075.

Fu, Y., Zhan, P., Chen, Q., & Jiao, H. (2022). Joint modeling of action sequences and action times in problem-solving tasks.. Retrieved from psyarxiv.com/e3nbc

Vehtari, A., Gelman, A., & Gabry, J. (2017). Practical Bayesian model evaluation using leave-one-out cross- validation and WAIC., 1413? 1432.

Gelman, A., Meng, X.-L., & Stern, H. (1996). Posterior predictive assessment of model fitness via realized discrepancies.,, 733?760.

Gelman, A., & Rubin, D. B. (1992). Inference from iterative simulation using multiple sequences.,, 457?511.

Han, Y., Liu, H., & Ji, F. (2022). A sequential response model for analyzing process data on technology-based problem- solving tasks.(6), 960-977.

Han, Y., & Wilson, M. (2022). Analyzing student response processes to evaluate success on a technology-based problem-solving task.(1), 33?45.

Han, Y., Xiao, Y., &Liu, H. (2022). Feature extraction and ability estimation of process data in the problem-solving test.,(6), 1393?1409.

[韓雨婷, 肖悅, 劉紅云. (2022). 問題解決測驗中過程數據的特征抽取與能力評估.(6), 1393? 1409.]

Hao, J., Shu, Z., & von Davier, A. (2015). Analyzing process data from game/scenario-based tasks: An edit distance approach.(1), 33? 50.

Harding, S. M. E., Griffin, P. E., Awwal, N., Alom, B. M., & Scoular, C. (2017). Measuring collaborative problem solving using mathematics-based tasks.(3), 1-19.

He, Q., Borgonovi, F., & Paccagnella, M. (2021). Leveraging process data to assess adults’ problem-solving skills: Using sequence mining to identify behavioral patterns across digital tasks., 104170.

He, Q., & von Davier, M. (2016). Analyzing process data from problem-solving items with N-grams: Insights from a computer-based large-scale assessment. In R. Yigal, F. Steve, & M. Maryam (Eds.),(pp. 749?776). Hershey, PA: Information Science Reference.

Hoffman, M. D., & Gelman, A. (2014). The No-U-Turn sampler: Adaptively setting path lengths in Hamiltonian Monte Carlo.(1), 1593?1623.

LaMar, M. M. (2018). Markov decision process measurement model.(1), 67?88.

Levy, R. (2019). Dynamic Bayesian network modeling of game-based diagnostic assessments.(6), 771?794.

Li, M., Liu, Y., Liu, H. (2020). Analysis of the Problem- solving strategies in computer-based dynamic assessment: The extension and application of multilevel mixture IRT model.(4), 528?540.

[李美娟, 劉玥, 劉紅云. (2020). 計算機動態測驗中問題解決過程策略的分析: 多水平混合IRT模型的拓展與應用.(4), 528?540.]

Liu, H., Liu, Y., & Li, M. (2018). Analysis of process data of PISA 2012 computer-based problem solving: Application of the modified multilevel mixture IRT model.1372.

Liu, Y., Xu, H., Chen, Q., & Zhan, P. (2022). The measurement of problem-solving competence using process data.,(3), 522?535.

[劉耀輝, 徐慧穎, 陳琦鵬, 詹沛達. (2022). 基于過程數據的問題解決能力測量及數據分析方法.(3), 522?535.]

Ma, W., Iaconangelo, C., & de la Torre, J. (2016). Model similarity, model selection, and attribute classification.(3), 200?217.

Man, K., Harring, J. R., & Zhan, P. (2022). Bridging models of biometric and psychometric assessment: A three-way joint modeling approach of item responses, response times and gaze fixation counts(5), 361?381.

Newell, A., & Simon, H. A. (1972).(Vol. 104, No. 9). Englewood Cliffs, NJ: Prentice-hall.

OECD. (2013).. OECD Publishing. http://dx.doi.org/10. 1787/9789264190511-en

Peng, S., Cai, Y., Wang, D., Luo, F., & Tu, D. (2022). A generalized diagnostic classification modeling framework integrating differential speediness: Advantages and illustrations in psychological and educational testing.(6), 940?959.

Rasch, G. (1960).. InProceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability: Held at the Statistical Laboratory, University of California, June 20-July 30, 1960 (Vol. 4, p. 321). University of California Press.

Rosen, Y. (2017). Assessing students in human-to-agent settings to inform collaborative problem-solving learning.(1), 36?53.

Shu, Z., Bergner, Y., Zhu, M., Hao, J., & von Davier, A. A. (2017). An item response theory analysis of problem- solving processes in scenario-based tasks.(1), 109?131.

Tang, X., Wang, Z., He, Q., Liu, J., & Ying, Z. (2020). Latent feature extraction for process data via multidimensional scaling.(2), 378?397.

Tang, X., Wang, Z., Liu, J., & Ying, Z. (2021). An exploratory analysis of the latent structure of process data via action sequence autoencoders.(1), 1?33.

van der Linden, W. J. (2006). A lognormal model for response times on test items.(2), 181?204.

van der Linden, W. J. (2007). A hierarchical framework for modeling speed and accuracy on test items.(3), 287?308.

Vista, A., Care, E., & Awwal, N. (2017). Visualising and examining sequential actions as behavioural paths that can be interpreted as markers of complex behaviours., 656?671.

Watanabe, S. (2010). Asymptotic equivalence of Bayes cross validation and widely applicable information criterion in singular learning theory.(12), 3571?3594..

Wilson, M., Gochyyev, P., & Scalise, K. (2017). Modeling data from collaborative assessments: learning in digital interactive social networks.(1), 85?102.

Xiao, Y., He, Q., Veldkamp, B., & Liu, H. (2021). Exploring latent states of problem-solving competence using hidden Markov model on process data.(5), 1232?1247.

Xiao, Y., & Liu, H. (2023). A state response measurement model for problem-solving process data., Online First.

Yuan, J., Xiao, Y., & Liu, H. (2019). Assessment of collaborative problem solving based on process stream data: A new paradigm for extracting indicators and modeling dyad data., 369.

Zhan, P., Jiao, H., & Liao, D. (2018). Cognitive diagnosis modelling incorporating item response times.(2), 262?286.

Zhan, P., Man, K., Wind, S. A., & Malone, J. (2022). Cognitive diagnosis modeling incorporating response times and fixation counts: Providing comprehensive feedback and accurate diagnosis.(6), 736?776.

Zhan, P., & Qiao, X. (2022). Diagnostic classification analysis of problem-solving competence using process data: An item expansion method.,(4), 1529?1547.

Zhan, S., Hao, J., & Davier, A. V. (2015). Analyzing process data from game/scenariobased tasks: An edit distance approach.,(1), 33?50.

Zhang, S., Wang, Z., Qi, J., Liu, J., & Ying, Z. (2022). Accurate assessment via process data.,(1), 76?97.

Zhu, M., Shu, Z., & von Davier, A. A. (2016). Using networks to visualize and analyze process data for educational assessment.(2), 190?211.

Binary modeling of action sequences in problem-solving tasks: One- and two-parameter action sequence model

FU Yanbin, CHEN Qipeng, ZHAN Peida

(School of Psychology, Zhejiang Normal University; Intelligent Laboratory of Child and Adolescent Mental Health and Crisis Intervention of Zhejiang Province; Key Laboratory of Intelligent Education Technology and Application of Zhejiang Province, Jinhua 321004, China)

Process data refers to the human-computer or human-human interaction data recorded in computerized learning and assessment systems that reflect respondents’ problem-solving processes. Among the process data, action sequences are the most typical data because they reflect how respondents solve the problem step by step. However, the non-standardized format of action sequences (i.e., different data lengths for different participants) also poses difficulties for the direct application of traditional psychometric models. Han et al. (2021) proposed the SRM by combining dynamic Bayesian networks with the nominal response model (NRM) to address the shortcomings of existing methods. Similar to the NRM, the SRM uses multinomial logistic modeling, which in turn assigns different parameters to each possible action or state transition in the task, leading to high model complexity. Given that actions or state transitions in problem-solving tasks have correct and incorrect outcomes rather than equivalence relations without quantitative order, this paper proposes two action sequence models based on binary logistic modeling with relatively low model complexity: the one- and two-parameter action sequence models (1P and 2P-ASM). Unlike the SRM, which applies the NRM migration to action sequence analysis, the 1P-ASM and 2P-ASM migrate the simpler one- and two-parameter IRT models to action sequence analysis, respectively.

An illustrated example was provided to compare the performance of SRM and two ASMs with a real-world interactive assessment item, “Tickets,” in the PISA 2012. The results mainly showed that: (1) the latent ability estimates of two ASMs and the SRM had high correlation; (2) ASMs took less computing time than that of SRM; (3) participants who are solving the problem correctly tend to continue to present the correct actions, and vice versa; and (4) compared with the fixed discrimination parameter of the SRM, the free estimated discrimination parameter of the 2P-ASM helped us to better understand the task.

A simulation study was further designed to explore the psychometric performance of the proposed model in different test scenarios. Two factors were manipulated: sample size (including 100, 200, and 500) and average problem state transition sequence length (including short and long). The SRM was used to generate the state transition sequences in the simulation study. The problem-solving task structure from the empirical study was used. The results showed that: (1) two ASMs could provide accurate parameter estimates even if they were not the data-generation model; (2) the computation time of both ASMs was lower than that of SRM, especially under the condition of a small sample size; (3) the problem-solving ability estimates of both ASMs were in high agreement with the problem-solving ability estimate of the SRM, and the agreement between 2P-ASM and SRM is relatively higher; and (4) the longer the problem state transition sequence, the better the recovery of problem-solving ability parameter for both ASMs and SRM.

Overall, the two ASMs proposed in this paper based on binary logistic modeling can achieve effective analysis of action sequences and provide almost identical estimates of participants' problem-solving ability to SRM while significantly reducing the computational time. Meanwhile, combining the results of simulation and empirical studies, we believe that the 2P-ASM has better overall performance than the 1P-ASM; however, the more parsimonious 1P-ASM is recommended when the sample size is small (e.g., 100 participants) or the task is simple (fewer operations are required to solve the problem).

process data, action sequence, problem state transition, action sequence model, item response theory

B841

2023-01-04

* 國家自然科學基金青年基金項目(31900795)資助。

詹沛達, E-mail: pdzhan@gmail.com