考慮泄漏的無桿式高壓氣動彈射器內彈道精確建模及試驗

王雪琴, 馬吳寧, 馬大為, 王尚龍, 張震東

(1.南京理工大學 機械工程學院, 江蘇 南京 210094; 2.陸軍研究院 工程設計研究所, 江蘇 南京 210016)

0 引言

隨著現代空天偵察技術的快速發展,對導彈隱蔽生存提出了更高要求,因而冷發射方式得到越來越廣泛的應用[1]。目前冷發射方式主要有燃氣式、壓縮空氣式、液壓式和電磁式等[2]。其中壓縮空氣式具有紅外暴露特征小、環境適應性好和設備重復利用率高等優點,能極大地降低發射陣地的紅外特征,提高生存能力[3]。但也帶來了極端工況下基于理想氣體的熱力性質參數較實際值會產生很大偏差,進而影響彈道參數真實性的問題[4]。

國外對于空氣氣體狀態方程的研究,經歷了從理想氣體狀態方程,到利用統計學方法考慮分子間作用力后導出的各種真實氣體狀態方程(范德瓦爾斯方程、維里方程、Redlieh-Kwong方程、Soave-Redlieh-Kwong方程[5]、Peng-Robinson方程[6]等),再到針對空氣的熱物性質進行了持續十多年的實驗數據測量,并由實驗數據擬合出標準干空氣熱力學狀態方程的發展過程。其中,由實驗數據擬合的標準干空氣熱力學狀態方程適用范圍最廣:溫度60～2 000 K,壓力0～2 000 MPa[7]。

國內關于氣動彈射內彈道建模研究,主要以理想氣體、絕熱和零泄漏假設[8-14]為主,只有較少數學者開展了考慮真實氣體效應的彈射內彈道建模方法研究。Ren等[15]、楊風波等[4,16]、Yang等[17]提出一種高壓空氣兩級三氣缸彈射裝置,基于改進的對應態維里方程,建立了考慮真實氣體效應的內彈道模型并進行了數值計算,研究表明高壓空氣的綜合做功能力偏離理想氣體,真實氣體效應研究必不可少。任銳等[18]研究了一種以壓縮空氣為動力源、油液為傳動介質,具備油液自緩沖結構的多級氣動液壓彈射裝置的彈射性能,基于真實氣體狀態方程——維里方程,建立了描述多級氣動液壓彈射過程的數學模型。姚琳等[3]提出一種新型高壓空氣驅動無桿式氣缸彈射裝置,引入真實氣體狀態方程——Redlieh-Kwong狀態方程,建立了考慮真實氣體效應、泄漏率為定值的無桿式氣缸彈射裝置內彈道模型。

上述研究大多基于理想氣體、零泄漏假設及非真實開閥過程的內彈道理論模型,或者基于真實氣體假設、非真實開閥過程且不考慮動態的內彈道理論模型。此外上述研究中使用的各種真實氣體狀態方程都只適用于一定壓力和溫度范圍。將真實氣體效應、動態泄漏及真實開閥規律同時考慮的內彈道理論模型研究鮮有報道。

本文針對壓力和溫度大范圍變化、固有結構存在一定泄漏的雙缸對稱無桿式高壓氣動彈射器開展動態泄漏測試試驗,基于美國國家標準技術研究所(NIST)發布的標準干空氣熱力學狀態方程,分別按理想氣體和真實氣體假設對比計算泄漏率,并擬合泄漏率隨壓力、行程變化的經驗公式;基于高壓空氣的真實熱力性質參數,建立考慮動態泄漏、真實氣體效應及真實開閥規律的精確內彈道模型,分別對考慮泄漏和不考慮泄漏兩種工況進行數值求解。對兩種工況下的數值結果進行對比分析,并詳細分析考慮泄漏的彈射過程中各熱力學參數和彈道參數的變化規律。最后將考慮泄漏工況的理論計算結果與彈射試驗數據及計算流體動力學(CFD)仿真結果對比,獲得了相對真實的彈道參數。

1 問題描述

本文提出的雙缸對稱無桿式高壓氣動彈射器模型,其結構簡圖如圖1所示。

圖1 雙缸對稱無桿式高壓氣動彈射器結構

該模型主要由高壓氣源(高壓室)、左右對稱分布的無桿式開口氣缸(低壓室)、托彈臺、緩沖機構等部件組成,其中核心部件無桿式開口氣缸如圖2所示。將無桿式開口氣缸呈雙缸對稱式分布,能顯著降低偏心載荷,減小彈射摩擦力,能效利用率更高。

圖2 無桿式開口氣缸結構圖

雙缸對稱無桿式高壓氣動彈射器的工作原理為:控制箱發出彈射指令后,閥控隨即響應,控制閥門打開;高壓氣體經過進氣管路流入氣缸(低壓室),當氣體對活塞的作用力大于負載自重及摩擦阻力時,活塞帶動動力輸出臂、托彈臺及負載一起運動;達到彈射行程后,兩側活塞組件撞擊到對應的緩沖油缸組件,負載飛離托彈臺,系統完成一次發射任務。

2 基于亥姆霍茲能的熱力性質參數

2.1 干空氣模型

以美國國家標準和技術局的標準空氣模型為基準,其組成為氮氣、氧氣和氬氣,各組成的體積百分比分別為78.12%、20.96%和0.92%。干空氣的參考常數如表1所示。

表1 干空氣的參考常數

2.2 干空氣的狀態方程

標準干空氣的狀態方程是基于現有實驗下的壓力p-密度ρ-溫度T、熱容、聲速和氣液平衡數據,使用最小二乘法擬合而來,該方程采用無量綱亥姆霍茲能的形式來表達:

(1)

式中:α(δ,τ)為無量綱的亥姆霍茲能,T為氣體溫度;a(ρ,T)表示亥姆霍茲能;R為空氣理想氣體常數;α0(δ,τ)為理想氣體對亥姆霍茲能量的貢獻部分(2.3節中簡寫為α0,上標0表示理想氣體性質),δ=ρ/ρm表示約化密度,ρm表示最大冷凝密度,τ=Tm/T表示約化溫度的倒數,Tm表示最大冷凝溫度;αr(δ,τ)為對亥姆霍茲能量的剩余貢獻部分(2.3節中簡寫為αr,上標r表示剩余性質);α0(δ,τ)、αr(δ,τ)的表達式分別如式(2)、式(3):

(2)

(3)

式中:系數N1～N19及ik、jk、lk的具體數值詳見文獻[7]。

2.3 熱力性質參數計算

用于計算壓縮因子Z、壓力p、比熱力學能u、比焓h的函數,可通過對亥姆霍茲能進行密度和溫度的微分計算如下:

(4)

p=ZρRT

(5)

(6)

(7)

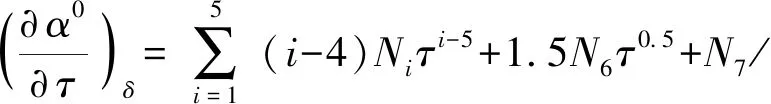
u=RT[a(τ)+b(δ,τ)]

(8)

h=RT[a(τ)+b(δ,τ)]+RTc(δ,τ)

(9)

3 無桿式開口氣缸彈射器泄漏試驗

無桿式開口氣缸的開口結構特點決定了彈射器存在一定程度的泄漏,泄漏率與氣缸內氣體質量流量及缸內壓力密切相關[19],直接影響到內彈道模型的預測精度。本文基于無桿式開口氣缸彈射器開展泄漏試驗,獲得不同缸內壓力和活塞行程下的泄漏率,并擬合出泄漏率與壓力、行程的經驗公式。

3.1 泄漏試驗方案及步驟

如圖3所示,泄漏試驗系統由無桿式開口氣缸、限位鋼管、高壓氣源、空壓機、干燥機、伺服閥、閘閥、安全閥、壓力傳感器、溫度傳感器和數據采集儀等組成。在活塞行程內取若干個固定位置,分別加載不同的缸內壓力,保持閥門打開約10 s時間,以保證足夠時間完成測試,測量并記錄氣源、缸內壓力及溫度等數據。高壓氣源容積約為2.5 m3,體積較大,導致不便對氣源內部進行溫度測量,因此假設高壓氣源溫度為一恒定值,僅測量缸內溫度變化。

圖3 泄漏試驗方案示意圖

在泄漏試驗中,由于活塞被限位鋼管限制在一定位置,長時間保持高壓有可能導致結構變形,為保證安全,泄漏試驗只做了低壓區域。考慮到無桿式開口氣缸動密封結構的設計原理為缸內壓力越高,密封處間隙越小,泄漏越小,因此低壓下泄漏率要大于高壓工況,低壓試驗下獲得的泄漏率能反映整個泄漏率外包絡。泄漏試驗主要步驟為:

1) 通過不同長度的限位鋼管,將活塞限制在不同行程l處(0 m、1.11 m、2.18 m、3.24 m、4.18 m、5.18 m);

2) 利用空壓機向氣源內充入高壓空氣;

3) 打開閘閥和伺服閥,使得高壓空氣進入開口氣缸中(缸內最高壓力p分別為1.77 MPa、2.76 MPa、3.76 MPa),并保持閥開10 s;

4) 通過數據采集系統,記錄保持閥開過程中氣源、氣缸的壓力時程曲線以及氣缸的溫度時程曲線;

5) 關閉閥門,釋放高壓氣體。為使數據可靠,每組試驗重復3次并取其平均值。

3.2 泄漏試驗過程

開展泄漏試驗,以缸內最高壓力3.76 MPa、活塞行程2.18 m的工況為例說明泄漏試驗過程,氣源壓力為4.2 MPa,在6 s時所有閥門打開,并保持10 s左右時間。試驗過程中工質泄漏如圖4所示。從圖4中可見泄漏試驗的直觀過程:閥門打開后氣缸即出現泄漏,泄漏處的高壓氣體形成白霧狀,隨著泄漏量的增大,氣霧團也變大。保持閥開過程中,氣源及開口缸內壓力時程曲線如圖5所示,開口缸內溫度時程曲線如圖6所示。

圖4 工質泄漏過程

圖5 壓力時程曲線

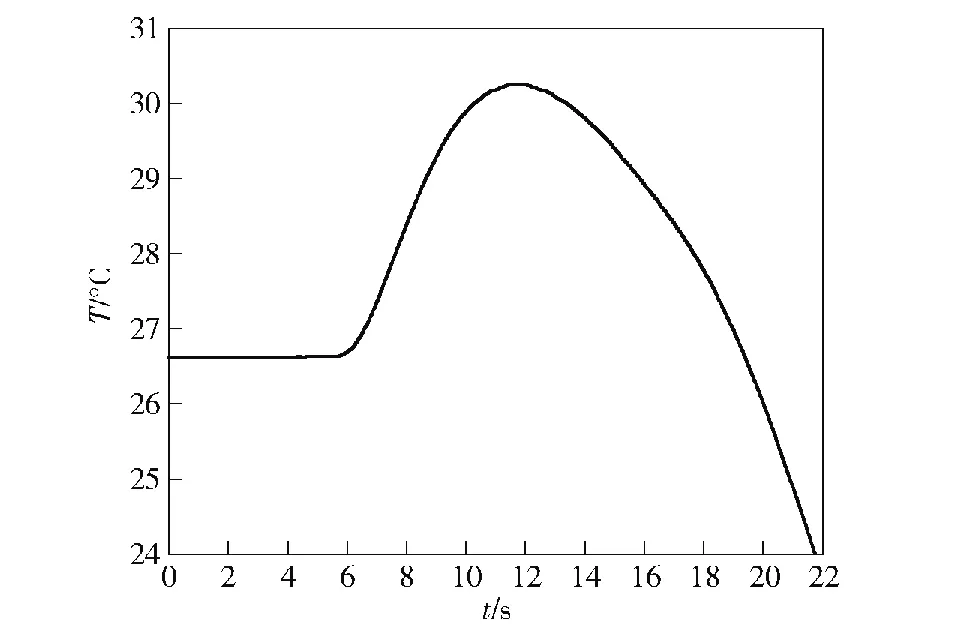
圖6 溫度時程曲線

從圖5中可以看出,6 s后,高壓氣體迅速從氣源進入氣缸,氣源壓力在不到1 s內快速下降,相對應地,缸內壓力迅速達到最高壓力3.76 MPa,隨后由于泄漏,缸內壓力從峰值開始下降,氣源壓力也慢慢下降,從圖6中可以看出缸內溫度呈先上升后下降的變化趨勢。

3.3 泄漏率計算方法及公式擬合

泄漏率的計算流程如下:

1) 根據圖5、圖6的壓力與溫度數據計算初始和最終時刻的氣源及缸內工質密度;

2) 將得到的密度分別乘以體積,獲得初始和最終時刻的氣源及缸內工質總質量;

3) 兩質量差值即為閥開過程中工質的泄漏量[20],再除以時間10 s,即可獲得單位時間內的泄漏率。

工質密度的兩種計算方式如下:

1) 將高壓氣體視為理想氣體,使用密度換算公式計算理想密度,如式(10)所示;

2) 將高壓氣體作為真實氣體,根據式(11)計算出真實密度。

(10)

(11)

式中:ρa=1.293 kg/m3;pa為標準大氣壓力。

分別使用上述兩種方法,得出不同缸內壓力p及活塞行程l下彈射裝置的泄漏率η,如表2所示。

表2 兩種計算方式下的泄漏率

從表2中可以看出以下規律:

1) 兩種計算方法下,泄漏率均隨著行程增加而增大,隨缸內壓力增大而減小;

2) 理想氣體假設下的泄漏率整體比真實氣體假設下的值小,經計算,理想氣體假設下泄漏率比真實氣體假設下泄漏率偏小的百分比最大約為4%;

3) 真實氣體假設下,泄漏率最小為2.5%/s,最大為3.38%/s,整體不超過4%/s。

對于規律1),可以從開口氣缸的密封結構特點角度解釋:行程越長,密封面越長,泄漏間隙長度也越長,從間隙處泄漏的氣體質量越大,故泄漏率隨之增大;缸內壓力越大,密封面處貼合越緊密,泄漏間隙越小,從間隙處泄漏的氣體質量越小,故泄漏率隨之減小。

根據規律2)可知,真實氣體假設下得到的泄漏率更為精確,根據這組數據,采用最小二乘法擬合出泄漏率η與壓力p、行程l的關系式為

η=3.188×10-2-1.808×10-3p+9.710×10-4l-8.763×10-8pl+1.700×10-5p2+1.784×10-6l2

(12)

4 無桿式高壓氣動彈射器內彈道模型

為簡化問題,做如下假設:

1) 工作過程時間短,假設系統絕熱;

2) 忽略氣體動能、勢能及氣體黏性;

3) 不考慮兩側氣缸的壓力不平衡因素;

4) 活塞達到推彈行程時,進氣腔與泄氣孔相通,氣體及時泄出,忽略剩余氣體對緩沖過程的影響。

4.1 伺服閥控制方程

彈射過程中通過閥門噴口的氣體有亞聲速和聲速兩種流動情況,噴口流量方程為

(13)

式中:ph為高壓室氣體壓力;Th為高壓室氣體溫度;pl為低壓室氣體壓力;μx為流量修正系數;A為閥開口截面積;γ為空氣絕熱系數。

閥門開啟規律對于內彈道控制有重要的影響,且與閥的開關原理及閥內結構直接相關,閥控系統直接控制閥芯運動及閥門的開啟。將閥門開口截面積A表示為閥芯位移d的連續函數,再通過位移傳感器測量并擬合出閥芯位移d-t函數,即可得出開口截面積A隨時間變化的連續函數。

為便于與下文彈射試驗結果對比,根據試驗所用閥的原理及結構,畫出閥的簡圖如圖7所示,得到閥的開口截面積A與閥芯位移d、閥門管道半徑r、輔助計算夾角θ的關系式如式(14)、式(15)所示。

圖7 氣閥簡圖

(14)

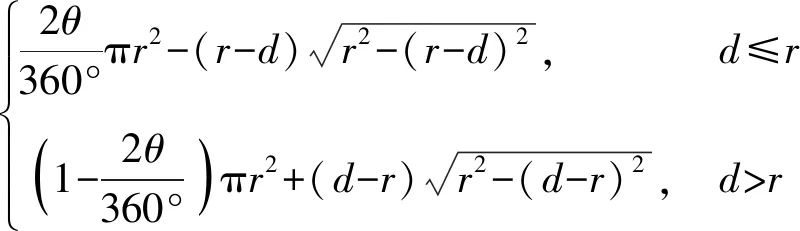
(15)

從式(15)中可以看出,開閥面積A是根據閥門管道半徑r及閥芯位移d計算得出的,最大開閥面積Amax與管徑r及閥芯最大位移值dmax均為正相關關系,閥門管道半徑r及閥芯最大位移值dmax通過影響最大開閥面積Amax進而對彈射內彈道產生影響。

4.2 高壓室控制方程

質量方程為

(16)

式中:ρh為高壓室氣體密度;Vh為高壓室體積。

能量方程為

(17)

式中:uh和hh分別為高壓室的比熱力學能和比焓。

4.3 低壓室控制方程

質量方程為

(18)

能量方程為

(19)

式中:ml為流入低壓室的氣體質量;ul為低壓室的比熱力學能;n為開口氣缸數目;S為活塞推力面積。

活塞運動方程為

(20)

式中:v為彈射速度;me為彈射質量;g為重力加速度;α為發射角。

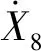
(21)

式中:V0為低壓室初始體積。

5 彈射內彈道結果分析

5.1 數學模型求解與結果分析

根據第4節中推導的考慮泄漏、真實氣體效應及真實開閥規律的精確內彈道數學模型,分別對考慮泄漏和不考慮泄漏兩種工況,在MATLAB 2014a軟件環境下,采用4階龍格-庫塔法編制數值程序,對微分方程組進行求解。計算所需參數及自變量初始值如表3和表4所示。

表3 模型中的相關參數

表4 自變量的初始值

圖8～圖12分別為考慮和不考慮泄漏的彈射過程中高低壓室的溫度變化、高低壓室的壓力變化、負載運動學參數變化及從高壓室到低壓室的質量流量變化曲線。從圖8～圖12中可以看出,考慮泄漏的彈射過程中高低壓室的溫度、高低壓室的壓力、負載運動學參數等曲線的數據均比不考慮泄漏的彈射過程中相關曲線的數據小;而考慮泄漏的彈射過程中從高壓室到低壓室的質量流量變化曲線的數據比不考慮泄漏的彈射過程中相關曲線的數據大。

圖8 高、低壓室溫度曲線

圖9 高壓室壓力曲線

圖10 低壓室壓力曲線

圖11 負載運動學參數變化曲線

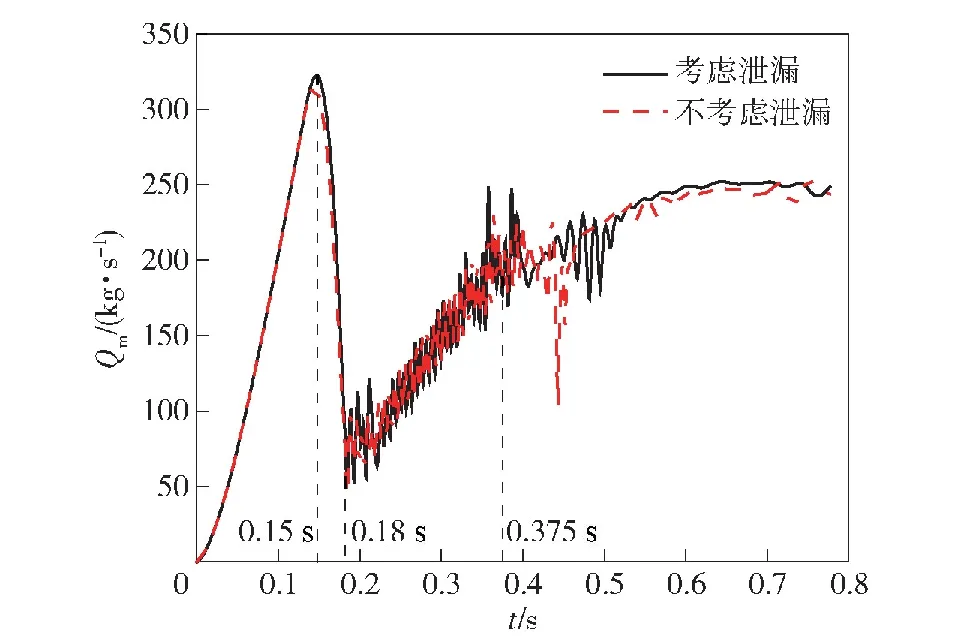
圖12 從高壓室到低壓室質量流量曲線

上述規律恰好體現了泄漏對彈射過程的內彈道有一定的影響:與沒有泄漏的工況相比,由于泄漏的存在,使得低壓室的壓力和溫度更低,推動負載運動所需的氣體質量更大,使得從高壓室流向低壓室的氣體質量流量也更大,造成高壓室的壓力及溫度下降得更快,最后反映到負載的運動上表現為相同時間內負載的過載更低,速度及位移更小。這樣就回到了分析的開始,分析過程自洽。

圖13給出了考慮泄漏彈射過程中泄漏率η的變化曲線。從圖13中可以看出,整個彈射過程中泄漏率在0.18 s之前呈現變小趨勢,在0.18 s以后慢慢變大。

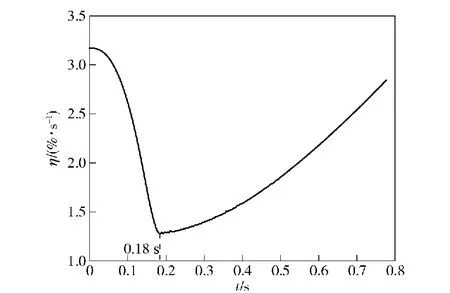
圖13 泄漏的質量流量曲線

結合圖11(a)及圖10可知,在0.18 s之前位移幾乎為0 m而低壓室壓力迅速增至最大值,在0.18 s之后位移開始增大而低壓室壓力呈下降趨勢。因此在0.18 s之前,泄漏率式(12)中-1.808×10-3p一項起主要作用,泄漏率減小;在0.18 s之后泄漏率式(12)中9.710×10-4l一項其主要作用,泄漏率慢慢增大,與3.3節中從開口氣缸的密封結構特點上解釋規律1)的內容相呼應。

5.2 考慮泄漏的彈射內彈道結果分析

圖14和圖15給出了閥芯位移及開閥面積的變化曲線。為便于分析,圖16中給出了考慮泄漏的彈射過程中高、低壓室及二者壓差的壓力變化曲線。

圖14 閥芯位移曲線

圖15 開閥面積A曲線

圖16 考慮泄漏的高、低壓室壓力曲線

由圖14可看出,閥門最大行程150 mm,閥門開啟動作響應時間0.375 s。由圖15可以看出,隨著閥門開啟,開閥面積A隨時間的變化率逐漸增大,0.18 s 之后開閥面積A近似線性增大,直至0.375 s閥門達到最大行程,開閥面積A達到最大值 0.030 8 m2,此時閥門完全開啟。

圖8(a)和圖8(b)曲線為考慮泄漏的彈射過程中高、低壓室的溫度變化曲線,所示溫度變化可分為3個時間段分析:

1) 0～0.18 s。在這個階段,隨著閥門的開啟,高壓室氣體不斷向低壓室流動,高壓室溫度迅速降低,低壓室溫度迅速升高。分析原因可知在 0.18 s 之前高壓室和低壓室的壓差很大(見圖16),高壓室內氣體以較大的質量流量沖入低壓室,使得高壓室氣體能量迅速降低,低壓室氣體的能量迅速升高。

2) 0.18～0.375 s。在這個階段,高壓室和低壓室的壓差很小,雖然開閥面積仍在增大,但此時隨著負載開始加速,低壓室容積逐漸增大,進而能量消耗逐漸加快。因此,低壓室溫度呈現下降趨勢,同時高壓室溫度繼續下降,下降速度比上一個階段小。

3) 0.375～0.777 s。在這個階段,開閥面積已經達到最大值,但此時負載速度及位移快速增大,能量消耗進一步加快。此時,高壓室溫度的下降速度比第2個階段大,同時低壓室溫度繼續下降。

聯系圖11(a)、圖12、圖15、圖16進行相互比照,將質量流量及壓力變化曲線分為4個時間段進行分析:

1) 0～0.15 s。高壓室初始壓力約為 13.2 MPa,高、低壓室的壓差很大(見圖16),在這個階段,高壓室流入低壓室的氣體質量流量快速增大,并在0.15 s左右達到最大值(見圖12)。同時,隨著閥門的開啟,開閥面積A逐漸變大(見圖15),高壓室氣體通過發射閥快速進入低壓室,導致高壓室壓力持續降低,低壓室壓力快速升高。

2) 0.15～0.18 s。在這個階段,雖然開閥面積A仍在增大,但高、低壓室的壓差相對變小(見圖16),式(13)中(pl/ph)2/γ-(pl/ph)(γ+1)/γ的值及高壓室壓力持續變小,此時質量流量出現下降趨勢,聯系圖11(a)在0.18 s之前位移幾乎為0 m,因此低壓室壓力仍持續增大,同時高壓室壓力持續降低,二者在0.18 s左右達到數值十分接近的狀態。

3) 0.18～0.375 s。在這個階段,雖然高低壓室的壓差很小(見圖16),但開閥面積A近似線性增大,式(13)中開閥面積A起主導作用,因此質量流量開始慢慢增大,在這個過程中高、低壓室壓力以及質量流量曲線均出現小幅波動,對此現象分析如下:

此時負載在低壓室推力的作用下慢慢運動(見圖11(a)),隨著質量流量增大,高壓室壓力減小低壓室壓力隨之增大,然而由于負載的運動,使得低壓室容積也增大,最后導致低壓室壓力降低,式(13)中(pl/ph)2/γ-(pl/ph)(γ+1)/γ的值隨之降低,使得質量流量開始變小,但是由于開閥面積A一直增大,使得質量流量又繼續增大,又回到分析的開始,如此反復數個周期。在這個階段低壓室容積增大部分的氣體量大于高壓室流入低壓室的氣體量,因此高、低壓室壓力均以幾乎相同的速率持續下降。

4) 0.375～0.777 s。在這個階段,發射閥全部打開,開閥面積A不再變化,在階段初期高、低壓室的壓差幾乎為0 MPa(見圖16),但隨著負載的加速運動,低壓室容積加速增大,低壓室容積增大部分的氣體量遠大于高壓室流入低壓室的氣體量,因此高、低壓室壓力均持續下降,且低壓室壓力下降速率大于高壓室,高、低壓室的壓差慢慢增大,式(13)中(pl/ph)2/γ-(pl/ph)(γ+1)/γ的值慢慢增大,質量流量也增大。

由圖11(a)中的實線可以看出,在0.086 s以前,由于活塞底部氣體推力未能克服負載重力以及靜摩擦力,彈體處于靜止狀態;從0.086 s起,活塞開始帶動托彈臺及負載加速運動,并在約9.6 m的彈射行程內加速至27.2 m/s(見圖11(b)的實線)。從圖11(b)中的實線可以看出:在0.15 s之前,負載速度很小;在0.15 s之后負載速度開始迅速增大,其隨時間的變化規律基本趨近于線性變化。聯系 圖(16)及圖11(c)中的實線可看出,彈射過程中負載過載系數的變化趨勢與低壓室壓力一致,原因也一致,在此不贅述。

5.3 理論仿真結果與試驗數據對比

基于雙缸對稱無桿式氣動彈射器原理樣機,搭建圖17所示彈射試驗測試系統進行彈射試驗,圖18 給出了某次彈射試驗的現場截圖。

圖18 彈射試驗現場截圖

為驗證理論模型的有效性,試驗測量了閥芯位移曲線、氣源與兩側開口氣缸內壓力變化曲線、過載曲線以及達到彈射最大行程時刻的速度值。

試驗環境溫度300 K,閥芯位移傳感器選用量程400 mm的日本Panasonic激光位移傳感器,非線性度小于±0.1%F.S.,壓力傳感器選用量程為 25 MPa 的瑞士Kistler傳感器,精度等級為0.5%F.S.,加速度傳感器選用中國工程物理研究院研制的無線三軸線加速度測量系統CBQ001,量程±100g,自帶電源及存儲功能。

限于試驗條件,無法直接測得負載的速度變化曲線,采用一組相隔Δs距離的光電開光安裝于彈射最大行程處(見圖17),當活塞經過一組光電開光后,采集系統分別采集到不同的光電信號,根據Δs及光電信號之間的時間差Δt,即可間接獲得該間距Δs范圍內的平均速度,即彈射最大行程時刻的速度。根據試驗中測得的負載加速度時間曲線,對其進行積分,得到速度-時間曲線,再對速度-時間曲線進行積分,得到位移-時間曲線。將試驗的測試結果與理論仿真結果進行對比,如圖19～圖21所示。

圖19 低壓室壓力曲線

圖20 高壓室壓力曲線

圖21 負載運動學參數變化曲線

通過光電開關數據計算出彈射末速度27.5 m/s,與仿真計算值接近。從圖19～圖21中可看出,高、低壓室的壓力及過載的測試結果在彈射前期及后期與仿真結果一致性很好,在0.15～0.5 s左右均出現一定程度的波動,且基本在仿真結果附近的范圍波動。

經過分析,認為出現波動的原因如下:在彈射中期,低壓室處于初始建壓完成狀態,此時開口氣缸內高壓氣體的流場狀態不穩定;此外,負載也剛開始低速運動,不穩定的壓力、導軌處復合摩擦狀態[21]等多種因素使得負載的運動呈現“卡頓”的狀態,表現在曲線上即出現波動。在彈射后期,開口氣缸內流場穩定,導軌處潤滑良好,負載速度越來越大,運動逐漸趨于穩定,曲線也不再波動。

5.4 CFD仿真結果與試驗數據對比

5.3節分析了高、低壓室壓力及過載的測試結果在0.15～0.50 s左右出現波動的可能原因,其中導軌處復合摩擦狀態這一現實因素在仿真計算中很難涉及,在此僅對不穩定流場狀態因素進行進一步的研究。

由于根據內彈道方程組求解的零維內彈道是基于“零維假設”,即不考慮高、低壓室壓力沿空間的分布,只考慮其隨時間的變化規律,同時也不考慮氣體在低壓室內的流動,因此該結果不能捕捉到多維時空特性場的規律,使得理論計算曲線與試驗曲線有一定的差異性。在此,基于計算流體力學方法,對雙缸對稱無桿式高壓氣動彈射器的彈射過程進行數值模擬(為簡化模型不考慮彈射過程中的泄漏),并將仿真結果與試驗數據進行對比。

雙缸對稱無桿式高壓氣動彈射器包括高壓氣源(高壓室)、左右對稱分布的無桿式開口氣缸(低壓室)、閥控及管路等如圖1所示,數值模型中將伺服閥簡化為垂直于管路的方塊。網格模型如圖22所示,采用六面體網格,閥門右側的網格作加密處理。

圖22 網格模型示意圖

基于壓力求解方法對彈射過程氣體流動規律進行求解,初始時刻高壓室賦壓力值為13.2 MPa,控制方塊按照圖14所示閥芯的運動規律模擬實際閥門的開啟過程,其與管路兩側采用交界面實現流場參數的傳遞,活塞的運動通過在氣缸軸向設置6自由度實現,動網格采用層動模式,其余邊界均為壁面邊界條件。

圖19～圖21給出了CFD仿真結果與試驗數據的對比曲線,其中高、低壓室壓力曲線均為體積平均壓力。圖23給出了0.375 s時刻的壓力云圖。

圖23 0.375 s時刻的壓力云圖

從圖19～圖21的曲線對比中可以看出,CFD仿真結果較好地捕捉到了多維時空特性場,其中高、低壓室的壓力及過載曲線也在0.15～0.5 s左右出現一定程度的波動,雖然與試驗數據相比仍有一定的差異,但與理論仿真結果具有良好的一致性。考慮到實際試驗過程中的復雜因素無法一一復現,在此認為仿真計算結果均與試驗結果總體基本一致,驗證了彈射原理及彈射過程內彈道模型的正確性。

6 結論

1) 兩種計算方式下泄漏率均隨著行程增加而增大,隨缸內壓力增大而減小;理想氣體假設下計算的泄漏率整體比真實氣體假設下的值小,偏小的百分比最大為4%;真實氣體假設下,泄漏率最小為2.5%/s,最大為3.38%/s,整體不超過4%/s。

2) 基于NIST發布的由實驗數據擬合的標準干空氣熱力學狀態方程,以真實熱力學參數為理論基礎,構建了考慮動態泄漏、真實氣體效應及真實開閥規律的精確內彈道模型,并分別對考慮泄漏和不考慮泄漏兩種工況進行數值求解。

3) 對兩種工況下數值結果進行對比分析,結果表明泄漏對彈射過程的內彈道有一定的影響,最后反映到負載的運動上表現為相同時間內負載的過載更低,速度及位移更小。給出了考慮泄漏的彈射過程中,高壓室放氣、低壓室充氣的詳細動態熱力學過程及彈道性能的詳細分析。

4) 進行彈射試驗,將考慮動態泄漏的仿真計算與試驗結果相比較:高、低壓室的壓力及過載的測試結果在彈射前期及后期與仿真結果的一致性很好,在彈射中期均出現一定的波動,但基本在仿真結果附近的范圍波動。

5) CFD仿真結果較好地捕捉到了多維時空特性場,其中高、低壓室的壓力及過載曲線也在彈射中期出現一定的波動,雖然與試驗數據相比仍有一定的差異,但與理論仿真結果具有良好的一致性。