基于深度強化學習的配件庫存決策研究

李雨情，潘超凡

（1. 西南交通大學制造業產業鏈協同與信息化支撐技術四川省重點實驗室，成都 611756；2. 西南石油大學計算機科學學院，成都 610500）

0 引言

隨著中國國民經濟的快速發展，我國的汽車工業也得到了迅猛發展。據公安部統計，2022 年全國機動車保有量達4.17 億輛，其中汽車3.19 億輛［1］。伴隨著汽車保有量的增長，汽車的保養和維修需求也迎來高峰期。眾所周知，汽車配件是汽車售后市場獲取利潤的直接源泉。由于汽車配件種類繁多，需求呈多樣性，根據需求發生間斷程度的大小，一般將汽車配件分為兩類：連續性需求配件和非連續性需求配件［2］。面對這樣不確定的配件需求，制定合理的庫存決策是企業急需解決的重大問題，也是擴大市場份額的重要支撐。本文根據配件的不同需求特性，通過深度強化學習算法研究汽車配件庫存決策問題。在現有研究的基礎上，本文的研究更貼合現實，也為企業庫存決策提供了一定的依據。

1 相關理論及方法

1.1 強化學習

強化學習（reinforcement learning，RL），是基于智能體與環境進行交互，并從環境中獲得信息獎賞并映射到動作的一種學習方式，如圖1所示，其主要思想是根據系統當前環境確定下一步決策應采取的行動，行動的結果是系統狀態發生轉移，而且根據行動的后果產生一定的獎勵評價決策的效果并進行反饋，從而逐漸改進決策方法［3］。RL 更接近于自然界生物學習的本質，因而在很多領域取得了成功的應用。

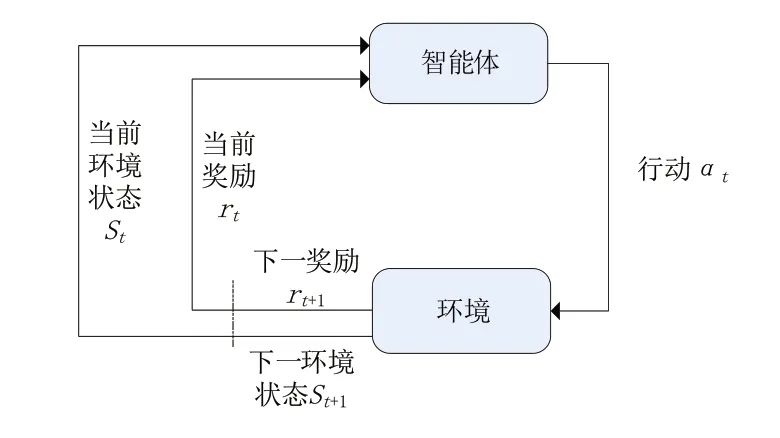
圖1 強化學習基本結構

隨著深度學習的興起，它與基于價值函數的RL算法結合產生了DQN［4］等深度強化學習算法［5］。而將深度學習與基于策略函數的RL結合，相繼產生了DDPG［6］，PPO［7］，TD3［8］，SAC［9］等算法。

1.2 基于強化學習的庫存決策研究

針對需求不確定的情況，目前大部分庫存決策研究方法通常分為兩步：首先建立需求預測模型得到預測的需求，其次設計算法求解待求問題的數學模型。這樣的研究方法需要依賴需求預測模型保證極佳的預測精度，難以考慮動態及隨機因素［10］。

而基于強化學習算法的庫存決策研究不依賴高精度的需求預測模型，且可充分考慮庫存決策過程中的多階段序貫決策和不確定性。庫存決策是一個典型的多階段序貫決策問題，Stranieri 等［11］將需求表示為余弦函數來模擬季節性行為，通過實驗比較VPG［12］、A3C［13］、PPO三種算法在兩階段供應鏈庫存決策問題下的性能，最終得出PPO 更能適應不同環境的結論，且PPO 的平均利潤也高于其他算法。畢文杰等［14］針對生鮮產品的易逝性提出了基于深度強化算法的生鮮產品聯合庫存控制與動態定價方法，通過DQN、DDPG、Q-learning 等算法進行對比實驗，結果表明基于DQN 算法的收益表現最佳。

綜上所述，考慮到產品需求復雜性的研究較少，而這是當前企業面臨的現實問題。本文針對這些問題，基于深度強化學習來建模求解庫存決策問題，以最大化期望總收益，并探討了不同需求下各前沿強化學習算法的表現優劣。

2 模型構建

2.1 問題定義

汽車制造廠內的配件中心庫是整個配件產業鏈的統籌計劃中心，其存儲了上萬種可能用于自身品牌汽車售后維修保養的配件，企業投入了大量人力和財力用于其日常運營。本文對由制造廠的配件中心庫和供應商組成的兩階段供應鏈庫存決策問題進行建模，從供應商訂購兩種不同需求特性的配件，滿足下級代理商的需求，如圖2所示。

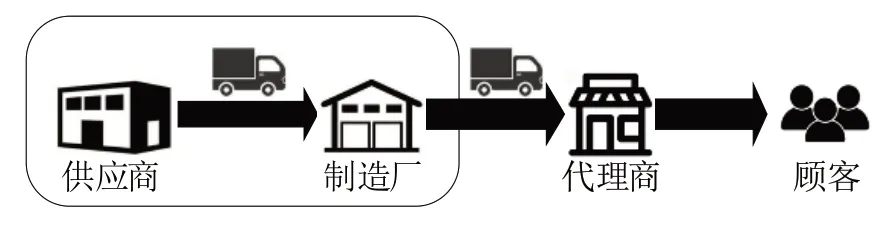
圖2 供應鏈結構

假設供應商可以提供無限數量的配件，從供應商到倉庫的交貨時間為零。假定制造廠有法律義務履行所有訂單，供應過程中允許缺貨，但是一旦缺貨，所欠的貨必須補上。其中各數學符號含義如表1所示。

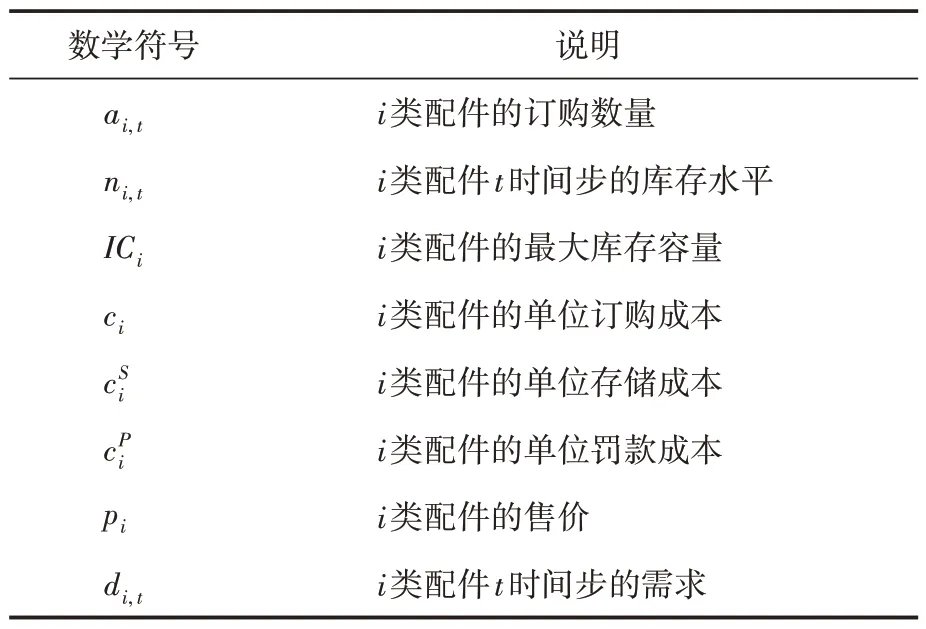
表1 數學符號含義說明

為了更貼合現實壞境，需求采用每個時間段的均值（λ）的泊松分布進行建模。連續性需求和非連續性需求的詳細設置將在第4節介紹。實驗中考慮1080 天的需求值，每15 天為一個時間步，故有72 個時間步。連續性需求和非連續性需求配件的需求值的某個實例如圖3所示。

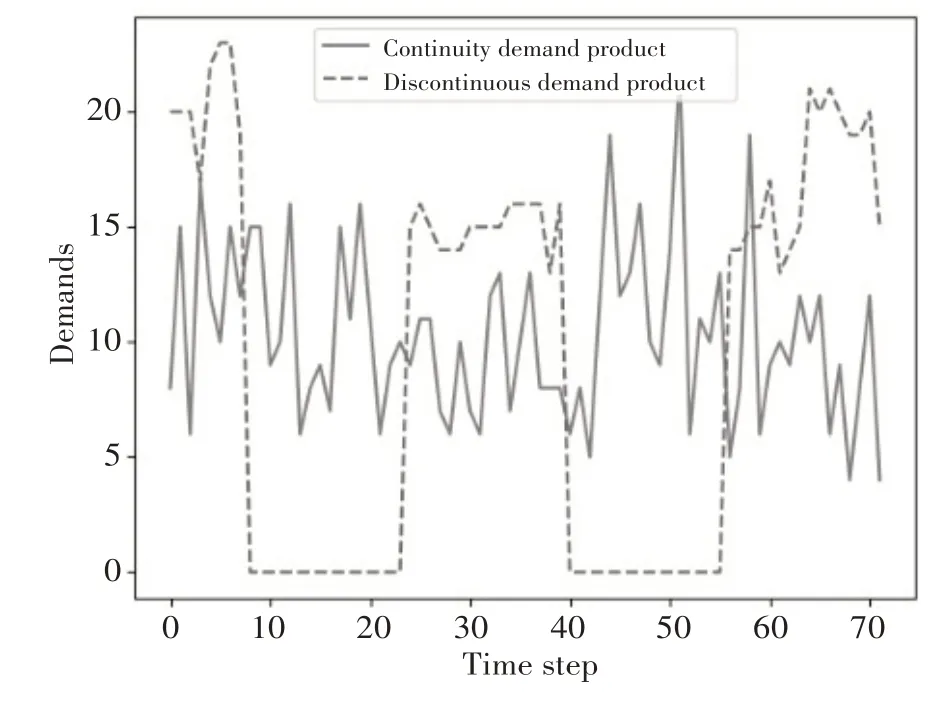
圖3 不同需求特性配件需求值的某實例

2.2 馬爾可夫決策過程

強化學習將庫存控制這類序貫決策問題建模為馬爾可夫決策過程并進行求解。本文通過馬爾可夫決策過程將待求解問題定義為一個四元組M=(S,A,P,R)，本文定義馬爾可夫決策過程的各要素如下：

狀態空間：狀態向量包括倉庫的每種配件類型的當前庫存水平，加上歷史x個時間步的需求值，并定義如下：

其中dt-1=(d0,t-1,d1,t-1,…,di,t-1)。當前t時間步的實際需求dt要到下一個t+1 時間步才能知道。類似于由Kemmer等［15］所做的工作，在后面加上需求值是為了使智能體可以從需求歷史中學習，從而將一種需求預測直接集成到策略中。

動作空間：通過神經網絡直接生成動作值實現了一個連續的動作空間，包括在供應商采購每種配件類型i的數量：

其中每個值的下界都是零，上限是倉庫對每種配件類型的最大容量，也即（0 ≤ai,t≤ICi）。

狀態轉移：下一狀態的更新規則定義為

在下一個時間步開始時，制造廠的庫存等于初始庫存加上訂購的數量，減去當前的需求。最后，更新包含在狀態向量中的需求值。

獎勵函數：每個時間步t的獎勵函數定義如下：

等式右邊的第一項是收入，第二項是訂購成本，第三項是存儲成本，實現max 函數是為了避免負庫存（積壓訂單）被計算在內。最后一項表示懲罰成本，它是用加號引入的，因為在不滿足訂單的情況下，庫存水平已經為負。因此，智能體的目標是利潤最大化。

3 算法設計

3.1 狀態抽象

強化學習中的狀態抽象是指將環境狀態映射到一個更低維的表示形式的過程。具體來說，在庫存決策環境中進行狀態抽象指的是對庫存狀態中與訂單決策不相關的狀態值進行映射，以達到狀態空間壓縮的效果。

本文針對庫存決策的環境提出一種基于狀態抽象的狀態歸一化模塊，該模塊設計了一個針對庫存決策的狀態抽象函數，使智能體能以更快的速度做出決策。基于訂單數量僅與一定范圍內的庫存水平相關的思想，本文設計了如下的狀態抽象函數：

其中s表示環境的狀態向量，狀態向量分為庫存水平和歷史需求兩部分，因此狀態向量的下限也分為兩部分，其中，需求下限為0，當積壓的訂單數大于制造廠每個t時間步訂購的數量at時，智能體都需要最大化訂單數量，因此狀態向量的下限需求的上限dh取決于需求的具體分布，當庫存水平高于兩倍需求的上限時，決策系統都需要將訂單數量設為0，以減小庫存成本，因此狀態向量的上限sh=(2dh,dh)。通過該狀態抽象函數可以將原始狀態空間S映射到新的狀態空間S′=[-1,1]中。

3.2 算法選取及設計

強化學習方法應用于庫存管理領域已經有一定研究，Q-learning 算法與DQN 算法應用較為廣泛。DQN 算法適用于離散動作空間，為了適用于連續動作空間，產生了DDPG 算法。和DDPG 相比，SAC 算法使用的是隨機策略，目標是最大化帶熵的累積獎勵，使其具有更強的探索能力，且更具有魯棒性，面對干擾的時候能更容易做出調整。

結合第2 節所設的庫存決策環境的SAC 算法流程如下：

輸入：環境

使用參數θ1、θ2、φ初始化策略網絡πφ、第一個評價網絡Qθ1和第二個評價網絡Qθ2。初始化經驗池B，設置其大小為N。

對于每一幕執行：

（1）初始化環境和狀態抽象后的狀態S0；

（2）從t= 1到t=T，執行以下操作：

①觀察狀態S從策略網絡中選擇動作A。

②執行所選動作A，觀察下一個狀態S′和獎勵r。

③在經驗池中存儲四元組(S,A,R,S′)。

④如果經驗池中存儲經驗的數量大于批次大小，執行以下操作：

（a）從經驗池中隨機采樣經驗批次(Si,Ai,Ri,S′i),?i= 1,…,N。

（b）使用兩個評價網絡中最小的Q值來計算目標值，利用梯度下降算法最小化評估值和目標值之間的誤差，從而更新兩個評價網絡Qθi。

（c）通過梯度上升算法更新策略網絡πφ。自動調整熵的系數α，讓策略的熵保持一種適合訓練的動態平衡。

（d）引入動量τ，用軟更新穩定訓練，更新目標網絡θ′i←τθi+(1 -τθ′i)。

SAC 算法是異策略的隨機策略梯度算法，在異策略的確定性策略梯度算法中，本文采用了相對于DDPG 算法優化的TD3 算法進行對比實驗。此外，同策略算法中也采用了較先進的PPO算法進行對比實驗。

4 仿真實驗

引入了深度神經網絡的算法模型的超參數一般需要手動設置，其中，學習率和gamma 值是深度強化學習模型訓練中非常重要的參數，影響到智能體訓練的穩定性和收斂性。因此，本文通過控制變量法，分別測試了學習率α=0.005、α= 0.001、α= 0.0005 的情況，最終選定α= 0.0005。固定其他參數，分別測試了gamma 值γ= 0.9、γ= 0.95、γ= 0.99 的 情 況，最終選定γ= 0.95。由于篇幅有限，具體效果圖不做展示。

本文設計并進行了一組豐富的實驗，分不同需求特性設定了三個場景，比較PPO、TD3、SAC 三種深度強化學習算法在不同場景下的性能，以此分析算法在仿真庫存決策環境中的表現，并判斷算法能否應用于現實環境。實驗中對i類配件的通用參數常量設置如表2所示。

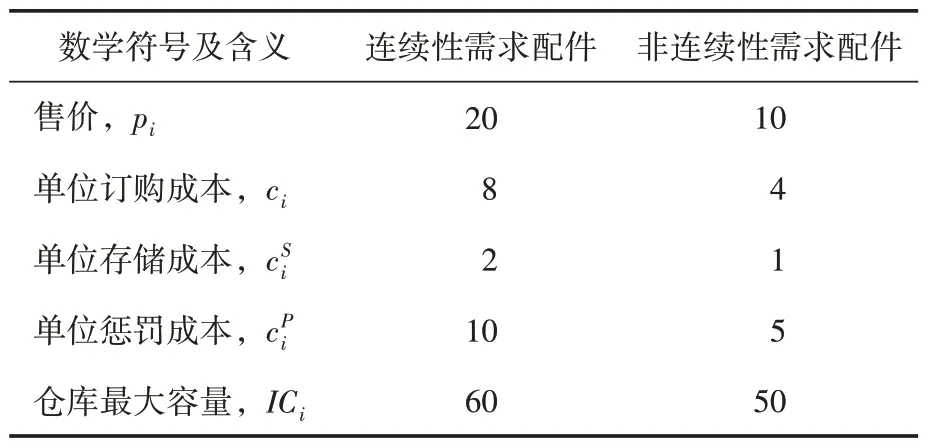
表2 實驗環境常量

4.1 連續性需求場景

本場景下的連續性需求配件的需求服從于均值為10 的泊松分布，結合上述參數設置進行實驗，對比分析TD3、SAC、PPO 三種深度強化學習算法在連續性需求下的性能。實驗結果如圖4所示，在連續性需求場景下，SAC和TD3算法的最終獎勵都比PPO 算法高，且SAC 算法和TD3 算法都比PPO 算法收斂穩定。SAC 算法比TD3 算法先收斂。盡管TD3 算法比SAC 算法先達到較高的獎勵，但TD3算法前期比較震蕩。

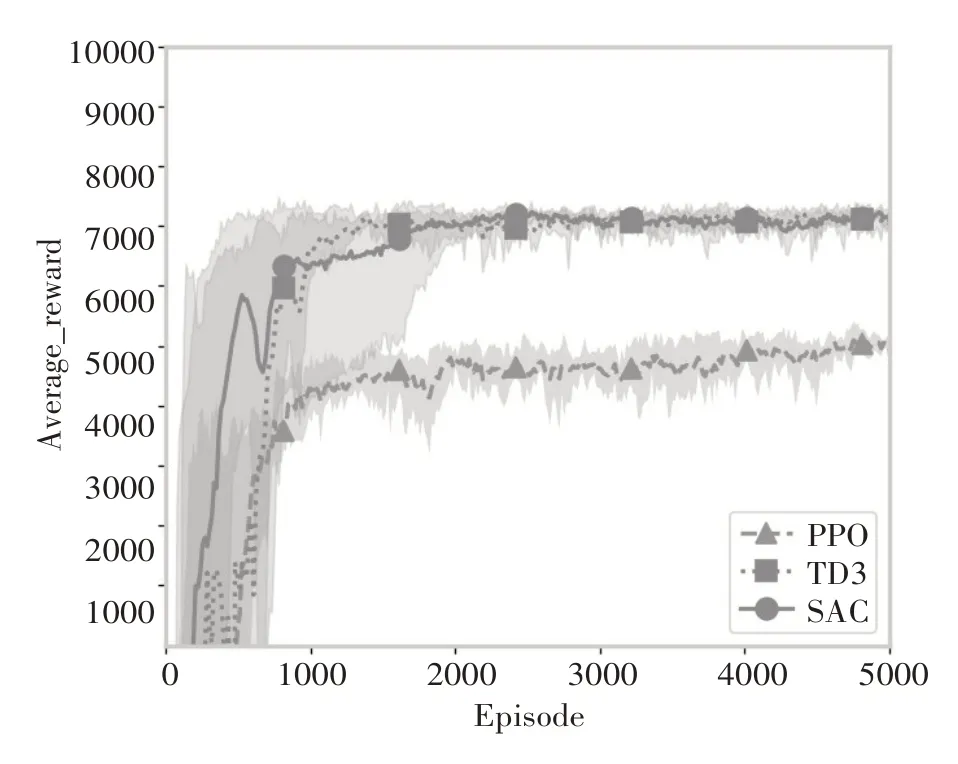
圖4 TD3、SAC、PPO在連續性需求下的實驗對比結果

4.2 非連續性需求場景

本場景下的非連續性需求配件的需求依然服從于泊松分布，均值每120天從［10，15，20，0］中等概率隨機選取。本研究結合上述參數設置進行實驗，對比分析了TD3、SAC、PPO 三種深度強化學習算法在非連續性需求下的性能。實驗結果如圖5 所示，在非連續性需求場景下，SAC 和TD3 算法都比PPO 算法獎勵高，且SAC算法和TD3 算法都比PPO 算法收斂穩定。SAC算法比TD3算法先收斂也先達到較高的獎勵。

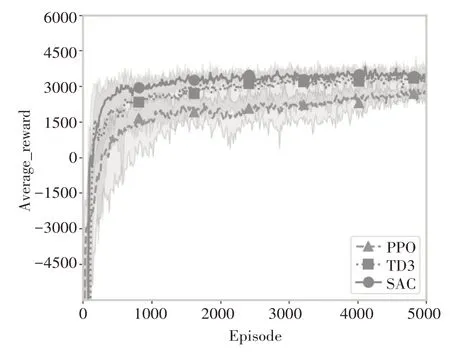
圖5 TD3、SAC、PPO在非連續性需求下的實驗對比結果

4.3 混合連續性及非連續性需求場景

本場景下配件的需求結合前兩節的需求設置，獎勵為這兩類配件的利潤之和。本研究結合上述參數設置進行實驗，對比分析TD3、SAC、PPO 三種深度強化學習算法在混合連續性需求和非連續性需求下的性能。實驗結果如圖6所示，在混合連續性需求和非連續性需求場景下，SAC 算法達到的獎勵最高，最先收斂，穩定性也最強；TD3算法其次，PPO算法最后。

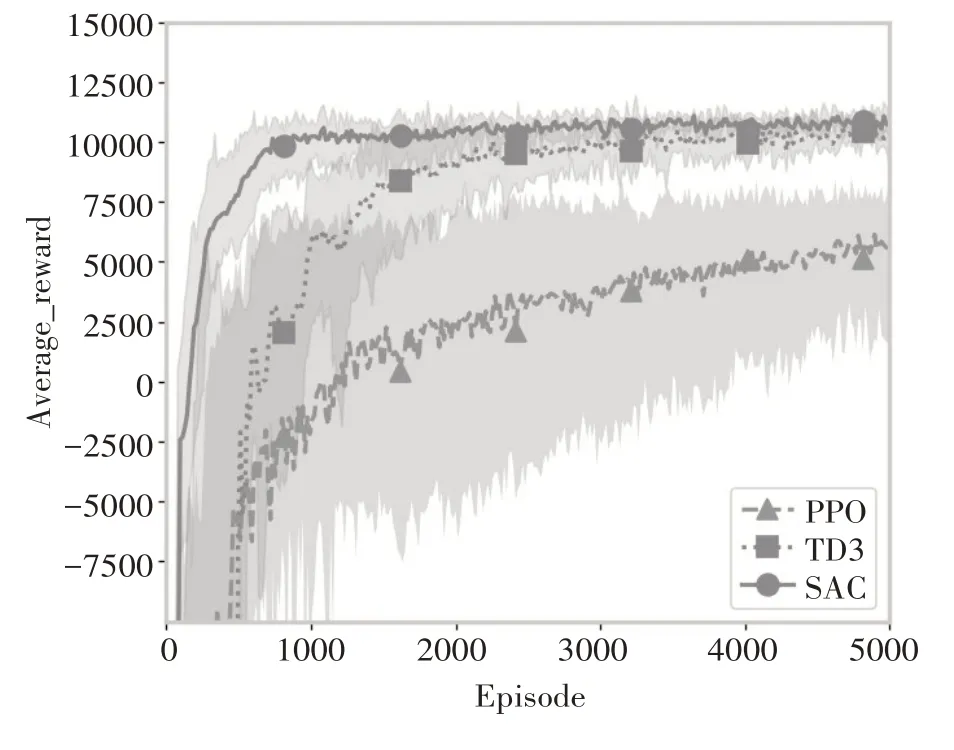
圖6 TD3、SAC、PPO在混合連續性及非連續性需求下的實驗對比結果

綜合上述三幅圖可得，SAC 算法的收益表現和穩定性無論在連續性需求、非連續性需求，還是混合連續性及非連續性需求上表現都最佳，其次是TD3算法，PPO算法的收益最低。

現實中的需求變化極其復雜，各種因素導致需求呈現隨機性強、非穩態的波動變化。SAC 算法能夠解決動態需求問題，也能為企業提供近似最優的訂貨策略。由此可見，基于SAC 算法的庫存決策模型具有非常廣泛的應用價值。

5 結語

目前汽車后市場規模相應擴大，配件需求也逐年遞增，對于制造廠而言如何合理控制庫存是非常重要的決策問題。本文研究了汽車配件的庫存決策問題，根據配件的需求特性，分為連續性需求配件和非連續性需求配件并制定了三個場景。通過將庫存決策問題建模為馬爾科夫決策過程，本文在更現實的實驗下評估了多個深度強化學習算法的有效性和穩健性。本文還設計了一個針對庫存決策的狀態抽象函數，從而有效減少無用狀態信息，簡化庫存決策環境，提高決策效率。

本文改進的深度強化學習算法，可以根據當前可用庫存來動態調整訂貨量，使預期利潤最大化。然而，由于條件限制，本研究只關注了兩階段供應鏈的庫存決策問題，未考慮運輸及訂購提前期等因素。未來可以在考慮運輸和訂購提前期等情況下的庫存決策方面進行深入的研究。