簡諧運動兩個定義的等價推證與實踐應用
許冬保 朱文惠
(1. 九江市第一中學,江西 九江 332000; 2. 九江市濂溪區第一中學;江西 九江 332000)
簡諧運動是最基本、最簡單的振動,是理想化的物理模型.現行教材[1-2]從運動學及動力學兩個視角,分別給出了簡諧運動的定義.由此引起教學上的困惑,為什么給出兩個定義?兩個定義是否是等價關系?在解決有關問題時,如何有效地選用定義來處理問題.
1 簡諧運動的兩個定義
1.1 定義1——運動學定義
如果物體的位移與時間的關系遵從正弦函數的規律,即它的振動圖像(x-t圖像)是一條正弦曲線,這樣的振動是一種簡諧運動.
1.2 定義2——動力學定義
如果物體在運動方向上所受的力與它偏離平衡位置位移的大小成正比,并且總是指向平衡位置,質點的運動就是簡諧運動.
1.3 等價性推證
定義1與定義2并非獨立的,兩者描述的角度不同,但兩者是等價的,由一個定義可以導出另一個定義.以下以彈簧振子為例進行分析.
1.3.1 由定義1導出定義2
如圖1所示,把連在一起的彈簧和小球穿在光滑水平桿上,彈簧左端固定在支架上,小球可以在桿上滑動,桿非常光滑,小球滑動時的摩擦力可以忽略,彈簧的質量比小球的小得多,也可以忽略.這樣就構成了一個彈簧振子.它是一個理想化模型.

圖1 彈簧振子簡諧運動模型
如圖1所示,使小球偏離平衡位置O一段距離,由靜止釋放小球,小球在回復力F作用下,以O點為平衡位置來回振動,在O點右側任意選擇一個位置P,該時刻t=0,相對O點的位移為x.若彈簧的勁度系數為k,選O為坐標原點,取向右為x軸正方向,小球相對平衡位置的位移x隨時間t按正弦(或余弦)規律變化.即
x=Asin(ωt+φ0).
(1)
由速度及加速度的定義,結合微分知識可得
(2)
(3)
對于某一時刻t,由式(1)(2)得到
(4)
上述表達式中,A、ω、φ0分別表示振幅、圓頻率、初相位.A、φ0由初始條件(x0,v0)確定,這里x0為初位移,v0為初速度.由式(1)(2)可得關系式[3]
由式(1)(3)知a=-xω2.結合牛頓運動定律,有F=-xmω2.令k=mω2,則
F=-kx.
(5)
1.3.2 由定義2導出定義1
如圖1所示,小球在P處,考慮到力F與x的方向,由胡克定律可以直接得到(5)式.同理,小球在O點左側某位置Q,所受回復力F具有與式(5)相同的形式.
設P處的加速度大小為a,由牛頓運動定律,有ma=-kx,即
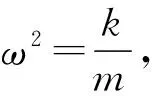
綜上,方程(1)(5)分別從運動學與動力學的視角描述簡諧運動,兩者是等價的,均可作為簡諧運動的判據.由上述分析還可以得到簡諧運動的周期公式
2 實踐應用
彈簧振子做簡諧運動,其位移、速度、加速度等物理量隨時間按正弦(或余弦)規律變化,并且對平衡位置具有時間、空間上的對稱性.由于簡諧運動的兩個定義是等價的,因此,在具體問題的分析中,可以根據問題的已知信息及待求的物理量,靈活地選擇相關定義來分析.
2.1 x-t表達式分析

(1) 振幅和周期; (2) 質點在t=0時受到的作用力.
評述: 理解簡諧運動位移表達式中各量的物理意義是解決問題的基礎.關于問題(2),也可以由定義2出發求解.根據k=mω2,得到k=6.25×10-3N/m.由于在t=0時,質點的位移為x=-6 cm,同樣由F=-kx可得作用力F=3.75×10-4N.
2.2 x-t圖像分析
例2.一彈簧振子沿x軸做簡諧運動,平衡位置在坐標原點.t=0時振子的位移為-0.1 m;t=1 s時位移為0.1 m,則
(C) 若振幅為0.2 m,振子的周期可能為4 s.
(D) 若振幅為0.2 m,振子的周期可能為6 s.
解析:由彈簧振子的x-t圖像進行分析.彈簧振子振動的位移設為x=Asin(ωt+φ0).若振幅為0.2 m,且t=0時刻,位移為-0.1 m, 即-0.1=0.2sinφ0,此時速度不為0,其振動方向可能遠離平衡位置,振動圖像如圖2所示;振動方向也可能指向平衡位置,如圖3所示.
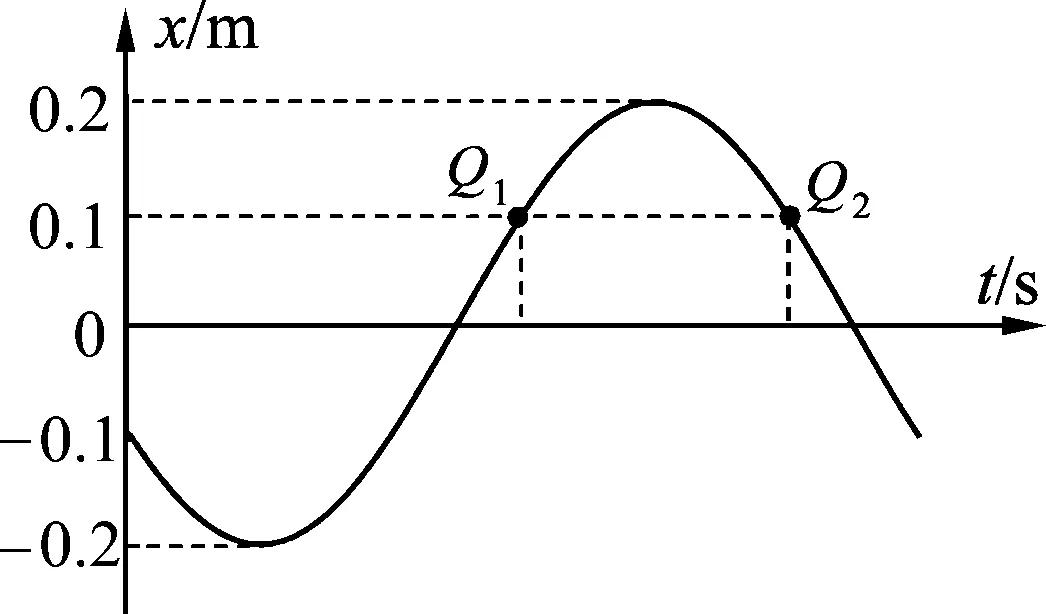
圖2 x-t圖像分析1

圖3 x-t圖像分析2

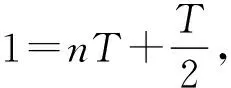


圖4 參考圓分析


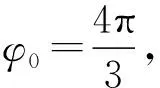
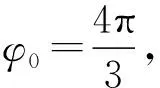
令n=0,上述各式中分別可得到Tmax.同樣,取振幅為0.1 m進行討論,所得結果同上.
2.3 動力學視角分析
例3.兩位外星人A和B生活在一個沒有自轉的勻質球形星體上,有一次他們決定進行一場比賽,看誰先到達星球的對徑位置.A計劃沿著星體直徑開一個隧道,采用自由下落的方式到達對徑位置;B計劃像衛星一樣沿著緊貼星球表面的空間軌道飛到對徑位置.問;誰會贏得這場比賽?(已知均勻球殼對其內部質點的引力為零)[4]

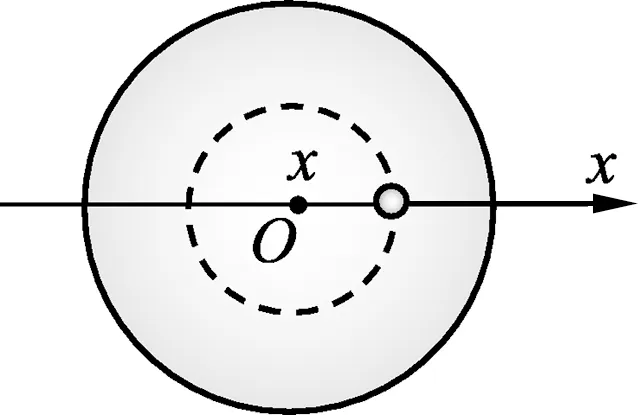
圖5 星體隧道中分析

由于TA=TB,則比賽以平局告終.
評述:由定義2得到,外星人A在隧道中做簡諧運動.導出的過程與彈簧振子做簡諧運動的推證相同.對于一個振動是否為簡諧運動的論證,從定義2出發思路清晰,自然流暢,合乎探究的邏輯脈絡.
2.4 多視角分析
例4.如圖6所示,固定在天花板上的輕桿將光滑輕質小定滑輪懸掛在空中,一根彈性輕繩一端固定在左邊墻壁上A點,另一端與套在粗糙豎直桿上P點、質量為m的滑塊連接,用手平托住滑塊,使ABP在一條水平線上.繩的原長與A點到滑輪距離AB相等,BP之間的距離為d,繩的彈力F與其伸長量x滿足胡克定律F=kx.滑塊初始在P點時對桿的彈力大小為mg,滑塊與桿之間的動摩擦因數為μ=0.2.現將滑塊由靜止釋放,當滑到Q點時速度恰好為0,彈性繩始終處在彈性限度內,重力加速度為g.
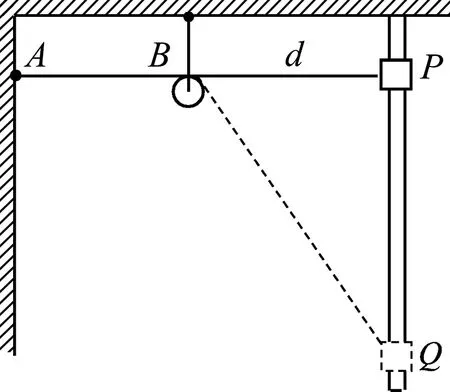
圖6 滑塊的振動
(1) 證明滑塊從P到Q的運動為簡諧運動;
(2) 滑塊從P到Q又從Q沿桿上滑速度再次減至零的整個過程通過的路程.
解析: (1) 證明滑塊的運動是簡諧運動,以下給出兩種方法.
視角1:定義2分析.


圖7 滑塊簡諧運動推證1
F=mg-Ff-FTcosα.
式中,Ff=μFN.由平衡條件及已知信息,得FN=kd=mg,因此

視角2:定義1分析.
若滑塊的運動是簡諧運動,參考圖7,則P、Q連線中點O為平衡位置,假設滑塊振動的振幅為A,由于在平衡位置O,滑塊的合力為0,故有mg=kA+μmg.已知kd=mg,則A=0.8d.
若某時刻通過任意位置M的速度為v,M相對平衡位置O的位移為x.由功能關系,有
式中,|Wf|為克服摩擦力所做的功,且|Wf|=μmg(A-x);ΔEp為彈性勢能的增加量,即
解得

(2) 視角1:定義2分析.
用定義2分析推證,方法同上.
如圖8所示,滑塊從Q沿桿上滑至任意位置M′,運動位移s′,令O′為平衡位置,相對O′位移大小為x′.取向上為正方向,滑塊在M′點受到沿桿方向的合力為
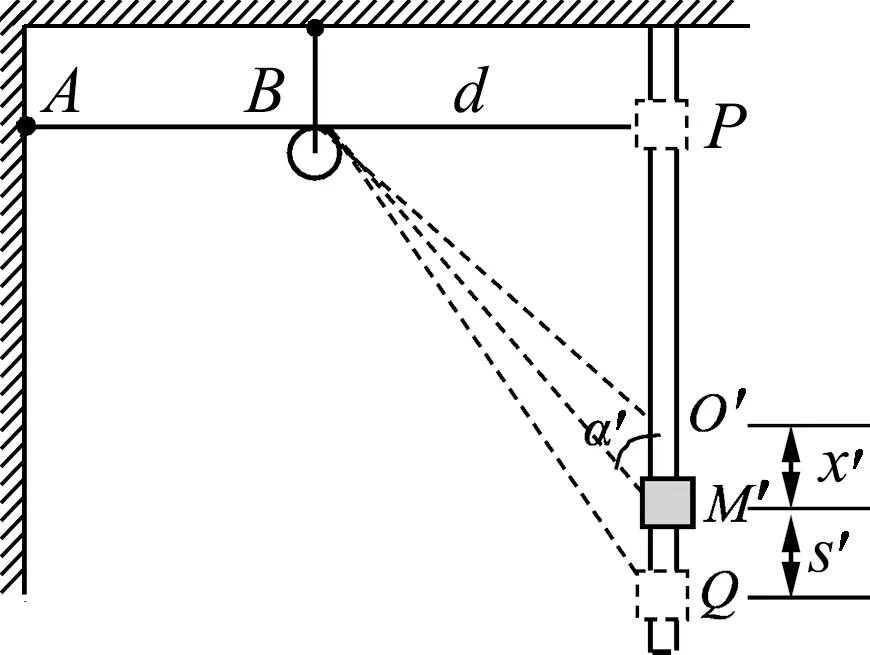
圖8 滑塊簡諧運動推證2
F=k(2A-s′)-mg-μmg=

視角2:能量觀念分析.
由問題(1)已得到,簡諧運動的振幅A=0.8d,對應的路程為l1=2A=1.6d;參考圖8,對于滑塊從Q上滑到速度減至0的過程,設該過程對應的路程為l2,根據能量守恒定律,有
(1+μ)mgl2.
解得l2=0.8d.因此,兩次振動的總路程l=l1+l2=2.4d.
評述: 彈性繩等效彈簧,彈性繩與滑塊構成彈簧振子模型.從定義1及定義2出發分析論證滑塊做簡諧運動.通過比較不難發現,用定義2推證滑塊的運動為簡諧運動,更加簡潔.教材上在分析單擺的運動為簡諧運動時,正是使用定義2進行推證.需要說明的是,本題中滑塊受到摩擦力作用,滑塊的振動屬阻尼振動,在振動過程中,交替改變平衡位置,振幅不斷減小,直到最后停下來.[5]但是在特定的半個周期(即從平衡位置的一端到另一端)內,由于阻力大小恒定,滑塊做區域簡諧運動.每個區域簡諧運動的時間均相同.若設問中只需求兩次振動的總路程,則用能量守恒定律或功能關系求解更方便.

