小球與斜面碰撞后的運動規律

李 都 姜付錦 張 蓓

(武漢市黃陂區第一中學,湖北 武漢 430300)

1 問題簡介

一個質量為m的小球以初速度v0發射,沿著拋物線運動,擊中斜面,然后反彈.忽略空氣阻力,因此軌跡由拋物線組成.假設撞擊過程沒有能量損失,忽略斜面摩擦力,因此,小球在碰撞過程中與斜面平行的動量分量不變,與斜面垂直的動量分量大小不變,方向反向.

本文研究了小球在與斜面連續碰撞過程中小球的運動規律.由能量守恒易得,小球不可能無限地向上爬升,因此必定在某個時刻會發生反轉并后退.在反轉之前有多少次向前運動的碰撞?動力學上是否允許在有限的時間里與斜面發生無限多次向前碰撞,類似于芝諾悖論中阿喀琉斯與烏龜的比賽一樣?小球在反轉后退時是沿著原來上升的路徑還是沿著不同的路徑?或者說在滿足什么條件的情況下,小球會沿著原來的路徑后退?

2 解法1:動力學的矢量分析

為了簡單起見,假設初速度矢量v0位于由斜面的法向矢量和重力加速度矢量所構成的平面內,因此,這個問題實際上是嚴格的二維問題,此時斜面實際上是一條斜線,很容易將該問題推廣到更一般的三維空間.

如圖1所示,為了描述小球的運動,建立以下兩對正交單位矢量:i沿水平向右方向,j沿豎直向上方向,m沿斜面向上方向,n垂直于斜面向上(斜面的法向方向).r(t)表示在任意時刻t小球的位置矢量,g為重力加速度的大小.以下討論某一次碰撞后小球的運動規律,設rk、vk′、vk分別表示小球與斜面發生第k次碰撞時刻tk時的位置矢量、碰撞前速度矢量、碰撞后反彈速度矢量(其中k=0,1,2…).

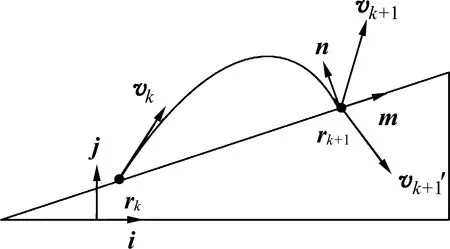
圖1 第k次碰撞示意圖

由牛頓第二定律得

(1)

在文獻[2]中已經證明勻變速直線運動的公式,在注意其矢量性后,確實可以用于勻變速曲線運動,所以在解平拋、斜拋類題目時可以用位移-時間公式和速度-時間公式.由速度-時間公式得

(2)

由位移-時間公式得

(3)

其中tk

(4)

由于rk和rk+1都在斜面上,所以斜面的法向量滿足

n·(rk+1-rk)=0.

(5)

由式(4)(5)得

(6)

整理式(6)得

(7)

當t=tk+1時由式(2)和式(7)得

(8)

vk+1是小球在tk+1時刻與斜面碰撞后的反彈速度,由動量守恒得

vk+1′·m=vk+1·m,

(9)

vk+1′·n=-vk+1·n.

(10)

由式(8)～(10)及矢量運算可得

vk+1=(vk+1·m)m+(vk+1·n)n=

(vk+1′·m)m-(vk+1′·n)n=

[(vk·m)m+(vk·n)n]-2(vk·n)n-

(11)

3 有趣的規律

如圖2所示為小球與斜面碰撞后運動軌跡草圖,斜面的傾角α,初速度矢量v0與斜面的夾角為β,v0為初速度的大小.

圖2 小球運動軌跡示意圖

(1) 所有的碰撞中,反彈速度具有相同的法線分量.

在式(11)兩邊同時點乘矢量n,并整理后得

vk+1·n=vk·n,k=0,1,2….

(12)

可得

vk·n=v0·n,k=0,1,2….

(13)

即在所有的碰撞中,反彈速度具有相同的法線分量,因此易得小球運動軌跡都與一個平行于斜面的公共平面相切,即小球運動軌跡的包絡面為與斜面平行的平面.設小球運動軌跡到斜面最遠的距離為hmax,將小球做的拋體運動沿斜面方向和垂直于斜面方向分解可得

(14)

(2) 任意相鄰兩次反彈之間的時間間隔相等.

設任意相鄰兩次反彈之間的時間間隔為T,由式(7)和式(13)得

(15)

將上式寫為標量形式為

(16)

由于相鄰兩次碰撞之間的時間間隔相等,在有限的時間內無限多次反彈類似于芝諾悖論中阿喀琉斯與烏龜的比賽那樣的時間積累是不可能的.

(3) 小球在向上運動過程中與斜面碰撞的次數N只與斜面的傾角α、初速度矢量v0與斜面的夾角為β有關.

由式(11)(13)得

(17)

在有限次反彈后vk的水平分量即

vk·i<0.

(18)

即小球相對于地面的運動開始反轉.

由矢量知識得

m·i=n·j=sinα.

則由式(17)(18)得向上運動碰撞次數

(19)

其中[]為取整函數.由矢量知識得

v0·i=v0cos(α+β),j·m=sinα,

v0·n=v0sinβ.

則(19)式寫成標量形式

(20)

有趣的是,向前碰撞的次數僅由角度α和β決定,與小球的初速度大小及重力加速度無關.由式(20)得當α或β足夠小時,向上碰撞的次數可以任意大,當α=0,β>0時,將有無限多次的碰撞,如果忽略能量損失和空氣阻力,有點類似于小時候玩的游戲“水上漂”.

(4) 返回路徑與前進路徑一致的充要條件為:cotαcotβ是正整數.

小球初速度斜向上,由能量守恒易得,小球不可能無限地向上運動,因此必定會在某個時刻向下運動,那么小球向下運動的返回路徑與向上運動的前進路徑在滿足什么條件下會完全重合?

① 類型1:cotαcotβ為正偶數.

如圖3所示,若在第k次碰撞時垂直撞向斜面,必定能垂直反彈回來,從而使返回路徑與前進路徑一致.即

圖3 類型1

vk·m=0.

(21)

在式(17)左右兩邊同時點乘矢量m聯立式(21)得

(22)

將其寫成標量形式得

cotαcotβ=2k.

(23)

當α和β滿足(23)式時,表示在k次碰撞時垂直于斜面,反向后的軌跡與向前運動軌跡相同.

② 類型2: cotαcotβ為正奇數.

如圖4所示,小球在第k次碰撞后反彈速度沿豎直方向,做豎直上拋運動,達到最高點后沿原路徑返回,即

圖4 類型2

vk·i=0.

(24)

在(17)式左右兩邊同時點乘矢量i聯立(24)式得

(25)

將上式寫成標量形式得

cotαcotβ=2k+1.

(26)

當α和β滿足(26)式時,表示在k次碰撞后速度沿豎直方向,做豎直上拋運動,達到最高點后沿原路徑返回.

4 解法2:矢量圖解法

得到上述有趣結論還可以用學生比較容易理解的矢量圖法,討論小球與斜面發生第k次碰撞后到再次落回斜面的過程設tk、rk、vk′、βk′、vk、βk分別表示小球與斜面發生第k次碰撞的時刻、位置矢量、碰撞前速度矢量、碰撞前速度矢量與斜面的夾角、碰撞后反彈速度矢量、碰撞后速度矢量與斜面的夾角(其中k=0,1,2…),小球落在斜面上,其實可以看作兩個分運動的合成,其位移矢量圖如圖5所示.

圖5 位移矢量圖

由正弦定理可得

(27)

其速度矢量圖如圖6所示,沿斜面方向和垂直于斜面方向建立直角坐標系,由正交分解得

圖6 速度矢量圖

g(tk+1-tk)cosα-vksinβk=vk+1′sinβk+1′.

(28)

由彈性碰撞得

vk+1sinβk+1=vk+1′sinβk+1′.

(29)

由式(27)～(29)得

vk+1sinβk+1=vksinβk,

即在所有的碰撞中,反彈速度具有相同的法線分量.結論1得證.