一種基于改進深度強化學習的加工成本型銑削參數優化方法

嚴勝利，李俊泓，李 浩，張春林

（廣安職業技術學院，四川 廣安 638000）

制造業的能源消耗隨著社會工業化的持續改善而增加[1]。準確預測加工過程中的能源消耗并優化加工參數以提高加工能源效率和節約制造成本具有重要意義[2]。

優化銑削參數的方法[3]包括：響應面法、粒子群優化算法、BP-SA 優化銑削參數的路徑、基于深度強化學習的銑削參數優化方法等。這些方法的目的是提高加工過程的能源效率，降低成本，并使銑削加工過程更加精確和高效。而基于深度強化學習的銑削參數優化方法是一種近年來新發展起來的方法，可以考慮加工成本，響應面法和粒子群優化算法是比較常用的方法。曾金平等[4]建立CNC 車床主軸加速能耗模型，并討論減少這部分能耗的潛在方法。在刀具磨損的不同階段，考慮切削能耗存在動態變化過程。因此，戚曉楠等[5]通過開發統一切削試驗工具磨損和能量圖，評估不同切削條件下的刀具磨損率和特定切削能量。為研究實際材料去除所消耗的能量，于碩等[6]在過程水平上定義了一個新概念，凈切削比能量，并建立每個完成硬銑加工水平的切削條件和能耗之間的關系。宣鵬舉等[7]關注的是熱輔助加工的能耗。此外，表面質量也是加工過程優化的關鍵目標之一。盧家鋒等[8]不僅建立不銹鋼銑削的經驗能耗模型，還基于RSM 方法建立表面粗糙度的預測模型，并優化節能和高質量加工的工藝參數。Fatoorehchi 等[9]使用反演分析方法分別建立切削力模型、殘余應力模型、工具壽命模型和表面粗糙度模型。然而，隨著加工能耗預測模型越來越完善，模型的計算也變得更加復雜。每個機床加工部件的能耗公式系數很多，分析和實驗校準的工作量增加。

本文提出的銑削參數優化方法基于深度強化學習，該方法具有較大的搜索時間優勢，并且采用粒子群優化算法可以獲得最佳優化效果。

1 研究基礎

1.1 反向傳播神經網絡模型解析

反向傳播神經網絡[10]（Back Propagation Neural Network，BPNN）是一種人工神經網絡，是一種多層前饋神經網絡，可以用于監督學習。BPNN 通過使用反向傳播算法來訓練網絡，該算法使用梯度下降法來最小化誤差函數。其網絡結構通常包括輸入層、隱藏層和輸出層，其中隱藏層可以有多個。BPNN 模型的訓練過程是在輸入數據和期望輸出之間進行的，通過不斷地調整神經元之間的連接權重，使得網絡的輸出結果逐漸逼近期望輸出。BPNN 模型在分類、回歸等任務中具有廣泛的應用。

反向傳播神經網絡模型優點在于高效性。BP 神經網絡的示意圖模型如圖1 所示。

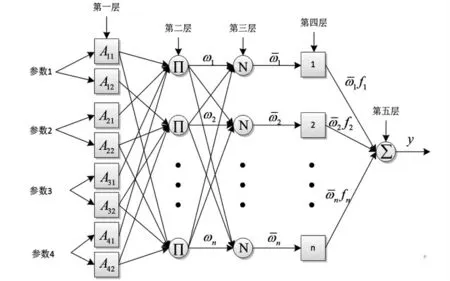
圖1 BP 神經網絡的示意圖模型

1.2 粒子群算法解析

粒子群算法[11]是一種群體智能優化算法，其靈感來源于鳥群或魚群等生物的行為。該算法通過模擬粒子在搜索空間中的移動來尋找最優解。每個粒子代表著搜索空間中的一個解，其位置和速度可以通過一定的規則進行更新，使其逐步向最優解靠近。在算法迭代過程中，每個粒子可以根據自身的最優解以及全局最優解進行位置和速度更新，以期望找到更優解。粒子群算法尋優過程如圖2 所示。

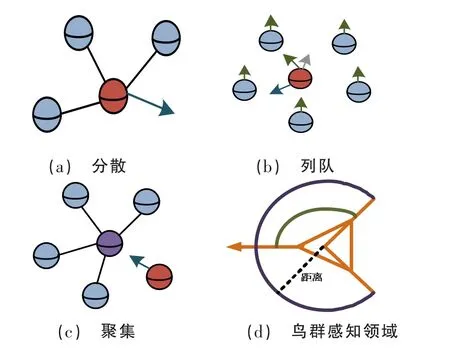
圖2 粒子群算法尋優過程

2 復合優化算法的參數優化解決方案

本文根據建立的目標函數模型和約束方程，上述模型均為非線性方程，如果采用傳統的優化算法（如遺傳算法、蟻群算法等），計算復雜，結果容易陷入局部最優。因此，引入一種組合優化算法，結合APSO（Adaptive Particle Swarm Optimization，APSO）和NGSA-II，以優化模型，獲得更精確的處理參數組合，新的組合優化算法可以充分發揮粒子群優化的收斂性和遺傳算法的種群多樣性。

2.1 自適應粒子群算法（APSO）

APSO 算法是一種群體智能算法，認為粒子處于n維空間中，根據一定規則傳遞信息，并根據信息的變化改變自身狀態生成的自組織行為。如圖3 所示為APSO算法中粒子之間信息傳遞模型。

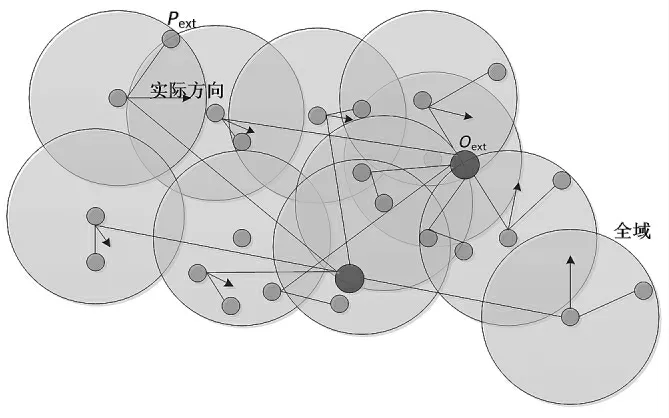
圖3 APSO 算法中粒子之間信息傳遞模型

該算法的步驟如下。首先，初始化一定規模的粒子群，當粒子群初始化時，每個粒子都有3 個屬性：適應度P，速度V 和位置X。其次，每個粒子將比較其當前位置的適應度值與其歷史中最佳適應度值pid，并將比較后的更好值作為當前最佳位置pext，否則不進行任何變化。粒子可根據式（1）和式（2）來更新速度和位置，直到達到設定的終止條件。

式中：w 為慣性權重因子，νid為粒子的速度，νid∈[-νmax，νmax]，c1、c2為學習因子，通常取c1=c2=2，r1d、r2d為相互獨立的均勻分布在[0，1]上的隨機數，xid為當前粒子位置。

2.2 改進的遺傳算法

改進的遺傳算法NSGA-II 采用非支配解排序方法和擁擠距離計算，并增加BPNN 神經網絡思想的精英策略。

2.2.1 基因編碼

基因編碼是遺傳算法設計中的關鍵問題。編碼方法必須考慮染色體的有效性、可行性、解空間表示的完整性。在NSGA-II 算法中，設備、工具和工藝順序的選擇需要在部分編碼方法中合理反映。對于處理參數的優化，采用編碼機制，種群中每個個體都有3 個子串。第一個分子串是工步號，第二部分表示相應的工具號，第三部分表示對應于工步的處理特征的平方表面編號。

2.2.2 交叉處理

改進的遺傳算法對于不同的子串，遺傳處理是不同的。相比于單點交叉，雙點交叉可以有效地減少位置偏差，而不會引入分布偏差。首先隨機選擇2 個染色體F1 和F2 作為親代染色體，在F1 中隨機生成2 個交叉點，然后將F1 的相應左右部分復制到后代染色體C1的同一位置，最后從F2 中移除F1 的左右部分，在C1染色體上復制原始后代C1 的一部分基因。以相同的方式，可以獲得另一個后代的C2 染色體。

2.2.3 突變處理

突變發生在交叉之后。突變是指將個體染色體編碼字符串中某個位點的基因值替換為該位點的其他等位基因，從而形成一個新個體。

2.3 基于APSO 和NSGA-II 的組合算法

與NSGA-II 相比，APSO 更加簡潔，收斂速度更快。然而，更新粒子位置主要依賴于將其自身位置與其周圍位置以及當前種群中的最優位置進行比較。這種模式相對簡單，使得其收斂速度在后期計算中不夠高效。

NSGA-II 具有4 個不同的進化步驟，包括選擇、交叉和變異，增加了解決方案的多樣性。當NSGA-II 解決到一定范圍時，會導致冗余迭代的低效處理，計算時間過長，解決效率低。因此，本研究將APSO 和NSGAII 結合起來，融合BPNN 思想，以提高算法效率。

組合算法的步驟總結如下。

步驟1：初始步驟。在可行區域內，APSO 生成p 個粒子并演化kmax度代數。所有粒子根據目標函數的值排序，然后將種群分為2 個子種群。優化的p/2 個粒子用作APSO 處理的初始種群p1。剩余的p/2 個粒子用作新一代染色體p2進行NSGA-II 處理。

步驟2：進化步驟。在尋找最優解的過程中，子種群p1 的位置和速度可根據式（3）—式（4）進行更新。

式中：xid為位置向量，νid為速度向量，k 為迭代次數，w為慣性系數。根據式（5）可知，p2中染色體的選擇概率與第i 個個體的目標函數值Fi有關。

步驟3：自適應處理。在傳統的遺傳算法中，由于種群規模有限，大多數個體都具有良好的目標函數值，并且這些良好的個體會被復制。其他個體在經過幾次進化迭代后被淘汰。但是當適者生存的過程失去控制時，缺乏多樣性和近親繁殖會出現，交叉和突變處理將失去效力，使算法更難跳出局部最優。

從上述的分析可以得知，基于種群早熟標記的適應性處理過程如下。程序開始時，將初始交叉概率和遺傳概率賦值為1。當算法計算出種群參數的目標函數值時，也會計算出交叉概率和遺傳概率。使用初始交叉概率和遺傳概率進行交叉變異，生成下一代的種群，計算新一代的種群參數。如果該參數大于預設值，這表明種群趨向于早熟，則使用交叉概率和遺傳概率重新生成一個新的種群；否則，初始交叉概率和遺傳概率仍然保留。在一定程度上，適應性處理可以有效地解決算法的早熟現象。為了確保每一代的最佳個體不會被破壞，算法收斂于全局最優解。

3 實驗分析

實驗設備：立式加工中心（型號：VDL-850A），VDL-850A 相關規格和參數見表1。根據第2.2 節和第2.3 節的分析，分別得到多目標函數的能耗目標函數和成本目標函數，并在實際約束條件下建立多目標函數的優化模型。在使用Matlab 編程和優化多目標函數時，需要在程序中輸入相關參數，并輸出最優解信息和最優目標值組合。對于能耗目標函數，使用Matlab編程和優化多目標函數，在程序中輸入目標函數的相關參數，對于成本目標函數，根據公式需要將相關參數輸入Matlab 程序中。

表1 VDL-850A 相關規格和參數

根據多目標函數模型和加工要求，設置相關參數如下。

1）工件材料：零件材料為45 鋼。

2）刀具：直徑為16 cm，齒數為3 cm 的高速鋼端銑刀，主角度。

3）加工要求：粗銑40 mm×40 mm 尺寸的臺階面，銑削深度為4 mm，銑削寬度為20 mm，長度為40 mm，在加工過程中使用切削液。

3.1 權重設置

基于先前建立的組合算法，只需要從第二步驟開始，以便獲得每個給定目標函數的不同權重系數。為方便解決多目標優化問題，通常難以同時獲得多個目標函數的最優解。為解決這個問題，將多目標函數轉化為單目標函數。線性加權法是最簡單的計算方法，權重可以通過主觀評價每個目標的重要性來分配。其中λ1+λ2=1，λ1和λ2分別是過程成本加權系數和能耗加權系數。在本研究中，這2 個因素在優化過程中被視為是同等重要的。因此，這里將權重設置為λ1=λ2=0.5。然后，新的目標函數可以用作評估函數。選擇不同的權重組合進行模擬分析和比較。

3.2 通過組合算法優化處理參數

為驗證所提出方法的有效性，應用組合優化算法解決多目標線性模型問題。使用Matlab 編寫程序，分別以多目標、單一目標最小成本和單一目標最小能量作為處理參數優化的目標。組合算法參數設置如下。

①設置初始種群數為30。②迭代次數k 為150，xid取0.9。③vid取0.4。以節能和低成本為優化目標，組合算法的迭代收斂過程如圖4 所示。通過以上分析，分別以多目標、單一目標最小成本和單一目標最小能量作為處理參數優化的目標。

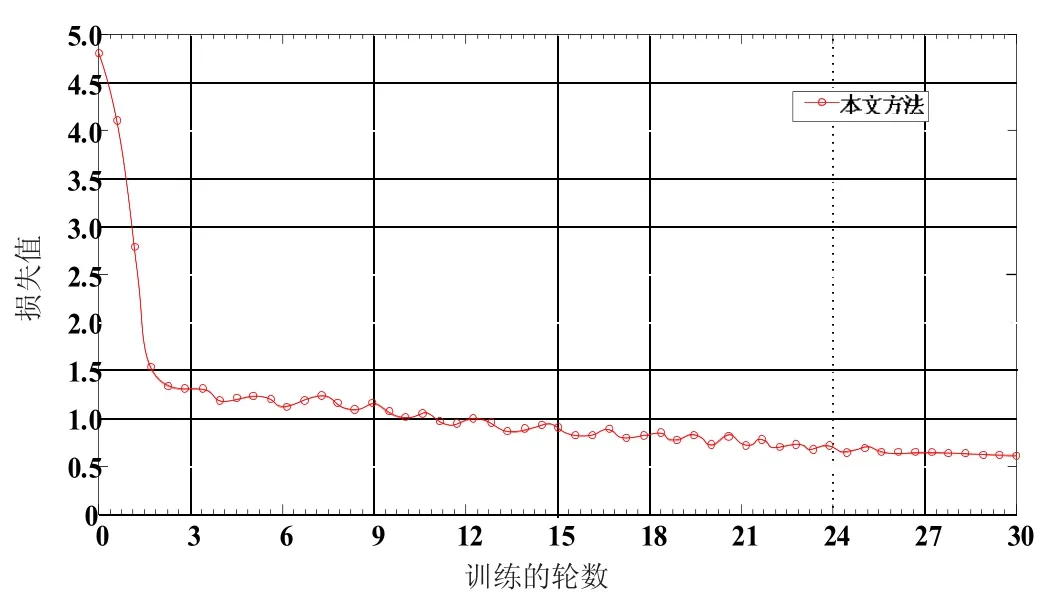
圖4 組合算法的迭代收斂過程

3.3 比較研究

本研究提出的多目標優化模型與單目標優化模型進行比較，可得以下結果。

1）以低加工成本為優化目標，銑削速度為28.51m/min，每齒進給為0.09 mm/z，加工時間為45.2 s，加工成本為46.17 元人民幣。單目標優化銑削速度較低，主軸轉速慢，刀具磨損小，加工成本低。但由于加工時間長，加工所需能量消耗達到3.475×105 J，因此，本文方法整體成本比單目標優化模型低。

2）以節能為優化目標，銑削速度為32.07 m/min，每齒進給為0.09 mm/z，加工時間為42 s，能量消耗為3.468×105 J。銑削速度和主軸轉速更快，加工時間更短，導致加工能量消耗更少。然而，單目標優化模型由于快速銑削速度導致刀具磨損增加，加工成本達到46.94 元人民幣，本文方法比單目標優化模型成本低。

4 結束語

在加工過程中，工藝參數的選擇直接關系到待加工零件的生產效率、成本和能耗。合理的工藝參數不僅可以提高生產效率，降低生產成本，還可以減少加工過程中的能耗。因此，設計優秀的組合算法，解決加工過程中能耗隨加工過程的動態變化問題，實現既能滿足加工中心節能降耗要求，又能兼顧其主要經濟指標的優化，方法意義重大。

本文首先設計了反向傳播神經網絡模型，采用APSO 算法、NSGA-II 算法與自適應粒子群算法的復合優化算法，提出優化銑削參數解決加工能耗的方案，并完成了基于APSO 和NSGA-II 的組合算法與單獨的APSO 方法或NSGA-II 方法比較。采用以VDL-850A型號的立式加工中心為實驗設備，針對能耗目標函數，使用Matlab 編程和優化多目標函數，分別以多目標、單一目標最小成本和單一目標最小能量作為處理參數優化的目標。

本研究提出的多目標優化模型與單目標優化模型進行比較，以低加工成本為優化目標進行分析，銑削速度較低，主軸轉速慢，刀具磨損小，加工成本低。以節能為優化目標進行分析，銑削速度和主軸轉速更快，加工時間更短，導致加工能量消耗更少。因此，本文方法無論從低加工成本目標和節能優化目標相比，均比單目標優化模型成本低。